Pentru fiecare mod de transport se pot distinge, în mod conventional doua componente (sectoare): pe de o parte infrastructura si serviciile de gestiune, întretinere si exploatare aferente, iar pe de alta parte prestarile de servicii folosind autovehicule, material rulant, nave sau aeronave. Din punct de vedere al structurii productive, aceste doua sectoare prezinta caracteristici tehnice si economice foarte diferite.
Infrastructurile de transport comporta indivizibilitati pronuntate care se traduc prin existenta unor costuri fixe importante. Lipsa de divizibilitate a sectorului implica faptul ca gestiunea nu poate fi realizata într-un regim de libera concurenta a unitatilor de productie distincte, care se confrunta pe piata[43]. Statul trebuie sa intervina pentru a obtine o alocare optimala a resurselor. Din contra, presupunând c& 24524i819y #259; infrastructurile exista, prestatiile de servicii constituie, în general, activitati divizibile.
Primii analisti ai productiei de transport si ai functiei costului de transport [44], , înca din deceniul 6 al secolului trecut, au demonstrat faptul ca masurarea agregata a productiei de transport prin tone.km sau calatori.km nu poate surprinde complexitatea serviciilor oferite de un operator oarecare de transport.
Astfel, de exemplu, atunci când se înregistreaza o crestere a costurilor unui operator cu 4% într-un interval de referinta cunoscut, în conditiile unei cresteri cu 5% a numarului de tone.km realizate, nu se poate preciza modul în care au fost generate aceste cresteri atât pentru costuri cât si pentru volumul prestatiei. Volumul traficului putea creste:
Prin definitie, functia de cost hedonic reprezinta functia de cost, cu o singura masura agregata a productiei (celelalte variabile caracteristice tipurilor de servicii realizate fiind la rândul lor agregate), echivalenta functiei de cost multi-produs, completa si cu variabile explicite, cum este cea din relatia (3.1).
Astfel, pentru estimarea unei functii de cost cu un mare numar de tipuri de productii oferite (cum este cazul deplasarilor între o multime de origini si o multime de destinatii într-o retea), se pot agrega productiile realizate într-o singura variabila, de exemplu tone.km.; alaturi de aceasta variabila agregata se introduc variabilele hedonice cum sunt, de exemplu, lungimea medie de transport, cantitatea medie de transport, numarul mediu de calatori transportati în unitatea de timp de referinta, proportia marfurilor transportate ca unitati de încarcatura etc.
Se poate constitui o functie de
productie hedonica 
, cu ajutorul careia se identifica functia de
cost hedonic, care este de forma:
(3.2)
Din punctul de vedere al estimarii, aceasta functie impune îndeplinirea unor conditii:
[48], obtinut cu cele mai scazute costuri este realizat pentru combinatia de consum de resurse K, L, F, care îndeplineste proprietatea:
(3.7)
Consumurile de resurse K, L, F din relatiile (3.6) care îndeplinesc proprietatea (3.7), conduc la functia de productie de forma:
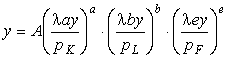, sau
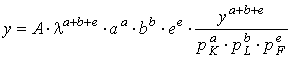(3.8)
Parametrul 
- costul marginal
pentru realizarea unei unitati suplimentare de productie, se
determina atunci:
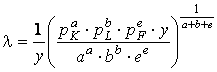(3.9)
Cu ajutorul relatiei (3.9) se obtin resursele K, L, F si functia costului de productie simpla:
(3.10)
Pentru functia
de productie de forma 
, continua si derivabila, definita pe
multimea numerelor reale pozitive, cu valori în acelasi domeniu, rata
marginala de substituire a primului factor cu cantitati din al
doilea factor pentru a mentine acelasi nivel de productie, y este:
,
iar elasticitatea substituirii factorului 1 cu 2:
O functie de cost de productie pe termen lung, cu structura translog, pentru n tipuri de servicii realizate, de dimensiuni yi, când sunt folositi m factori de productie, la preturile pj, are forma:
(3.12)
Pentru ca functia de acesta forma sa fie omogena de gradul întâi în raport cu preturile, trebuie îndeplinite conditiile:
,
În plus coeficientii trebuie sa fie simetrici astfel încât sa aiba o forma simpla a derivatei de ordinul 2.
Atunci când în datele experimentale se înregistreaza si valori nule, utilizarea unei forme translog pentru functia de cost devine problematica datorita valorii infinite pentru logaritmul unei valori nule.
Utilizarea unei astfel de functii de cost prezinta avantajul urmator: de cele mai multe ori, din practica uzuala, se dispune de date legate de valoarea alocata din costul total pentru fiecare factor de productie, iar acest fapt întrebuintat adecvat, poate îmbunatati precizia estimarii functiei de cost total.
Astfel, pentru factorul al carui pret este pi, se poate formula ecuatia care identifica proportia de cheltuieli alocata acestui factor, din costul total:
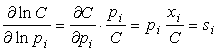(3.13
)
Esantionul de date poate include valoarea 0 pentru unele observatii. Asa este cazul, de exemplu, al anumitor sectii de circulatie de cale ferata care au valori pozitive ala traficului de marfa si calatori, în timp ce altele sunt specializate doar pentru traficul de marfa (cu trafic de calatori nul). În acest caz specificarea functiei translog este problematica, deoarece logaritmul din valoarea 0 este egal cu -
Rezolvarea problemei a condus la dezvoltarea asa-numitei "transformate Box - Cox" .
Daca datele referitoare la y sunt uneori nule, atunci în loc de a introduce datele ca log yi, cu transformata Box-Cox, aceste date sunt introduse ca:
(3.15)
[55], demonstreaza ca nu exista importante randamente de scara pentru transportul pe calea ferata, rutier sau aerian, în schimb, de cele mai multe ori, s-au obtinut importante randamente de densitate.
Decidentii politici sunt deseori interesati de masura în care economiile de densitate pot afecta competitia între modurile de transport.
De exemplu, pentru un operator de cale ferata cu un randament de densitate semnificativ, posibilitatea de a creste pretul va fi limitata daca pe acea zona se va confrunta cu operatori rutieri si/sau fluviali si/sau cu transportul prin conducte.
[57] din transporturi au relevat ca:
nu exista complementaritate de cost sau non-complementaritate în transportul de marfuri si calatori, pe calea ferata;
pot exista economii de specializare a celor doua tipuri de servicii pe calea ferata. Cu alte cuvinte, se pot înregistra reduceri ale costurilor totale rezultate din separarea operarii pe calea ferata a serviciilor de marfa de cele de calatori;
se manifesta dizeconomii de scop în cazul operarii comune a productiei de transport de marfa cu vehicule rutiere de mare capacitate alaturi de cele usoare;
în transportul aerian se manifesta, în mica masura o complementaritate de cost pentru transportul planificat (cu orar) si cel charter, în timp ce pentru transportul de calatori si cel de marfa s-au determinat non-complementaritati de cost;
[58] care evidentiaza faptul ca în sectorul transportului de marfa, în unitati de încarcatura mai mica decât autocamioanele, se manifesta un randament de scara crescator, generat de efectele economice de densitate.
Quinet, E. (1993) Transport between Monopoly and Competition. Transport Economics (ed.) Polak, J. and Heertje, A., Blackwell Publishers, Oxford, p.33-51.
|
