Analiza Riscului de Portofoliu prin Utilizarea Modelelor GARCH: Studiu de Caz

Autor: Catalin Cristian Darasteanu*

Abstract

Riscul de portofoliu reprezinta o problema extrem de delicata pentru fiecare investitor. Acest lucru este normal deoarece comportamentul investitorilor in pietele de capital este determinat in principal de relatia risc-randament.

Prezentul articol isi propune sa analizeze riscul de portofoliu printr-un exemplu practic. In particular, vom incerca sa modelam riscul unui portofoliu dat. Aceasta va fi realizata cu ajutorul modelelor GARCH, instrumente deosebit de utile in econometria financiara aplicata, care isi au originea intr-un studiu realizat de Robert Engle (1982).

Studiul isi propune sa depisteze cel mai bun model pentru analiza riscului unui portofoliu dat in perioada 1999-2001. De asemenea vom incerca sa depistam care sunt perioadele cu volatilitate mai pronuntata. Impactul alegerilor generale din noiembrie 2000 precum si a atacurilor teroriste asupra Statelor Unite din septembrie 2001 asupra portofoliului construit va fi analizat succint.

Cuvinte cheie: risc de portofoliu, diversificare, modele GARCH, autocorelatie, randamente reziduale, alegeri generale, atacuri teroriste asupra S.U.A.

I.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p;   Introducere

Metoda celor mai mici patrate si in particular regresia lineara reprezinta o mare realizare in domeniul econometriei. Aceasta este normal de vreme ce economistii sunt adesea tentati de descoperirea trendurilor viitoare ale unor anumitor evenimente economice. In studiul pietelor de capital, tentatia de a previziona randamente este una

deosebita. Multe studii si modele au incercat sa descopere care este trendul viitor al randamentelor, pornind de la un set de informatie din trecut, multime care include deseori comportamentul preturilor, raportul PER, capitalizarea bursiera etc. O interesanta teorie in acest domeniu este teoria mersului aleator ("the random walk hypothesis").

Adesea insa, econometricienii sunt chemati sa realizeze o previziune a riscului activelor finaciare. Modelarea acestuia a capatat si are o semnificatie deosebita astazi in cadrul teoriilor pietelor financiare. In particular, specialistii au acordat o larga atentie randamentelor reziduale, avand in vedere ca aceastea au o infleunta deosebita asupra randamentelor studiate.

Randamentele reziduale

Randamentele reziduale reprezinta acea parte a randamentelor care nu au fost capturate de catre variabila independenta a unui anumit model. De exemplu, sa consideram modelul de piata:

unde:

- randamentul titlului individual in perioada de timp t;

- termenul constant;

- riscul relativ de piata al unui titlu individual;

- randamentul portofoliului de piata;

- termenul eroare.

Randamentele reziduale sunt reprezentate tocmai de termenul al ecuatiei, indicand care este partea de randament a unui titlu individual ce nu a fost influentata de randamentul portofoliului de piata. Deseori, aceste randamente reziduale au o pondere foarte importanta in cadrul randamentului individual. De exemplu, Darasteanu (2002) aplica modelul de piata prin utilizarea celor mai mici patrate pentru a testa celebrul CAPM. Studiul arata ca randamentele reziduale au un impact deosebit, iar coeficientul de determinatie R² ajustat a demonstrat ca r_m are o influenta de pana la 10% asupra randamentului individual.

II.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p;    Caracteristici ale Seriilor Financiare

Gestiunea riscului portofoliilor de investitii a condus la necesitatea incercarii de modelare a sa. In particular, s-a investigat modul in care poate fi modelata dispersia conditionala. Numim prin dispersie conditionala dispersia unei serii de date care nu are o evolutie uniforma pe tot intervalul. Practic, acest fenomen poarta numele in econometrie de heteroschedasticitate si reprezinta o incalcare a supozitiilor care stau la baza metodei celor mai mici patrate, respectiv cea de homoschedasticitate. In fapt exista un volum larg de literatura de specialitate care dezbate caracteristicile evolutiei in timp a randamentelor. Marea parte a studiilor surprind faptul ca dispersia variaza ca amplitudine in timp.

Adeseori in practica, seriile financiare se dovedesc a nu urma o distributie normala. Seriile sunt mai degraba leptocurtice, adica exista o abatere larga a valorilor extreme de la media lor. Aceasta inseamna ca daca valoarea normala a indicelui Kurtosis (cel care arata cat de "ingrosate sunt extremitatile" sau cat de mult se abat valorile maxime si minime de la media lor) este 3, in seriile finaciare indicatorul ia valori mult mai mari (vom vedea acest lucru in exemplul practic propus). De asemenea, seriile financiare tind sa fie asimetrice. Aceasta inseamna ca valoarea indicelui Skewness (care suprinde simetria sau asimetria unei serii) ia valori diferite de zero.

Seriile financiare mai prezinta 2 probleme deosebit de importante:

1. corelatie seriala regasita in reziduuri;
2. heteroschedasticitate, adica evolutia neuniforma a dispersiei respectivei serii de-a lungul perioadei de timp analizate.

Intr-un interesant si binevenit studiu pentru bursa romaneasca, Alexandru Todea (2002) realizeaza o analiza tehnica a titlurilor cotate la categoria intai a Bursei de Valori Bucuresti si arata ca randamentele reziduale pentru marea majoritate a actiunilor nu sunt autocorelate. De asemenea, folosind un interval de timp diferit, Darasteanu (2002) arata de asemenea ca majoritatea actiunilor cotate la categoria intai nu prezinta reziduuri autocorelate (totusi multe din actiunile cotate la categoria a doua prezinta autocorelatie). Aceste rezultate prezinta o importanta aparte si au implicatii asupra teoriei pietelor eficiente .

III.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Modelele GARCH : Motivatie

Modelele GARCH sunt proiectate tocmai pentru a modela serii economice ce prezinta caracteristicile prezentate mai sus. Denumirea GARCH reprezinta:

• G - generalizat;
• AR - autoregresiv;
• C - conditional;
• H - heteroschedasticitate.

Primul model a fost realizat de catre Robert Engle in 1982. In fapt, acesta a fost un model ARCH. Modelul cuprinde o ecuatie pentru medie si una pentru dispersie, respectiv:

unde:

y_t - variabila dependenta in perioada curenta;

x_t - variabila independenta perioada curenta;

g - coeficient care arata influenta variabilei independente asupra variabilei dependente;

e_t - termenii reziduali in perioada curenta;

- dispersia variabilei dependente in perioada curenta;

w - constanta ecuatiei dispersiei;

a - coeficientul "ARCH";

e_t-1 - termenii reziduali din perioada precedenta;

- dispersia variabilei dependente in perioada precedenta;

b - coeficientul "GARCH".

Modelul descris mai sus este in fapt modelul GARCH (1,1) in care primul numar arata ca asupra dispersiei actioneaza termeni reziduali din perioada precedenta, iar cel de-al doilea numar arata ca dispersia din perioada precedenta are influenta asupra dispersiei curente. In fapt, pentru serii foarte mari, modelul GARCH (1,1) poate fi generalizat la modelul GARCH (p,q) .

Pentru ca aplicatia noastra se refera la analiza riscului unui portofoliu, ne vom concentra atentia numai asupra ecuatiei dispersiei. Modelul poate fi utilizat cu succes in studiile de volatilitate. Spre deosebire de metoda celor mai mici patrate, modelul GARCH include in ecuatia sa atat termenii eroare (adesea denumiti "socuri") cat si fenomenul de heteroschedasticitate. De asemenea este util in cazul in care seriile nu sunt distribuite normal, ci mai degraba au extremitati ingrosate. Nu mai putin important este faptul ca intervalele de confidenta pot varia in timp si deci intervale mai precise pot fi obtinute prin modelarea dispersiei randamentelor reziduale.

O interesanta abordare a modelelor GARCH este cea a posibilei existente a unui efect de levier. In fapt, modelul GARCH (1,1) este un model simetric si presupune ca termenii reziduali au acelasi semn. In realitate insa adeseori seriile financiare prezinta asimetrie. Un model foarte util in acest caz este modelul EGARCH sau altfel spus modelul GARCH exponential introdus de catre Nelson (199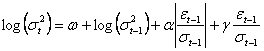1):

(1)

Efectul de levier poate fi testat prin testarea inegalitatii g<0 si . Notam ca acest model este asemanator modelului GARCH (1,1). Totusi, se remarca prezenta termenului log care transforma modelul intr-unul non-linear. De asemenea termenii reziduali sunt raportati la dispersie, devenind practic reziduuri standardizate.

IV.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p;  Date si Metodologie

Pentru construirea portofoliului au fost utilizate date din perioada 04.01.1999-22.12.2001, cuprinzand un numar de aproximativ 755 de observatii. Am utilizat in analiza noastra indicii BET si RASDAQ-C si cursul de schimb ROL/USD. Datele privind evolutia indicelui BET au fost oferite de Bursa de Valori Bucuresti, datele privind evolutia indicelui RASDAQ-C au fost culese de pe site-ul oficial al Societatii de Bursa Rasdaq, in timp ce sursa evolutiei cursului valutar ROL/USD o reprezinta Banca Nationala a Romaniei.

In aplicatia noastra, presupunem ca un investitor este dispus sa investeasca o parte a avutiei sale in piata de capital romaneasca. Investitorul are o toleranta semnificativa la risc, dorind totusi sa isi diversifice investitia. Presupunem ca acest investitor prefera investitii pe piata bursiera. Mai precis, presupunem ca 50% al capitalului sau este investit la prima categorie a Bursei de Valori Bucuresti (pentru simplificarea simularii luam ca activ financiar indicele de piata BET), 30% in piata extrabursiera Rasdaq (respectiv in indicele de piata Rasdaq-C), in timp ce pentru o mai buna diversificare si o protectie impotriva riscului va investi 20% in moneda americana (investitorul dorind astfel un grad de lichiditate semnificativa).

Investitorul nostru este interesat sa isi monitorizeze investitia si in acest sens el doreste sa stie cum a evoluat riscul portofoliului sau. De asemenea, ar vrea sa stie care au fost cauzele care au determinat anumite varfuri de volatilitate. Astfel, el va alege metodologia GARCH pentru analiza volatilitatii.

Primul pas va fi testarea prezentei semnaturii ARCH asupra portofoliului. Aceasta se va realiza cu ajutorul corelogramei radicalului randamentelor. Daca se observa existenta semnaturii ARCH vom trece la modelarea dispersiei conditionale. In acest sens, modelul GARCH (1,1) va fi comparat cu EGARCH (1,1). In sfarsit, dupa alegerea celui mai potrivit model, vom testa existenta unor termeni reziduali reminiscenti cu ajutorul corelogramei radicalului termenilor reziduali standardizati si prin aplicarea testului ARCH LM.

Pe baza datelor primare au fost calculate randamente zilnice (ale indicilor BET si Rasdaq-C si a cursului valutar). Apoi, pe baza procentelor mentionate mai sus a fost compus portofoliul si au fost calculate randamentele zilnice ale portofoliului. Datele au fost transferate ulterior in Eviews 3, unde au fost realizate toate testele necesare.

V.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Analiza Realizata, Rezultate Obtinute si Discutie

In primul rand vom prezenta o statistica primara a datelor. In tabelul urmator consideram randamentele zilnice ale indicilor BET si Rasdaq-C precum si a cursului valutar ROL/USD. Pe ultima coloana a fost considerat portofoliul construit.

Tab. 1: Statistici descriptive

Tabelul indica faptul ca cea mai riscanta a fost piata bursiera (daca ne raportam la indicele BET). Cel mai redus risc a fost inregistrat pe piata valutara (lucru asteptat de altfel). Deviatia standard a portofoliului a fost redusa semnificativ prin echilibrarea portofoliului cu moneda americana, inca o dovada clara a diversificarii. Notam de asemenea randamentul mai ridicat al monedei americane decat cel al indicelui BET.

Tabelul indica de asemenea faptul ca toate cele 4 serii, inclusiv portofoliul construit, nu urmeaza o distributie normala. Lucrul este evidentiat de valorile indicatorilor Skewness si Kurtosis. Valori extrem de mari se observa in cazul randamentului indicelui Rasdaq-C si in cazul randamentului monedei americane. Toate cele 4 serii sunt asimetrice. In particular, valorile situate pe exrema dreapta sunt foarte mari semn ca in anumite zile s-au inregistrat cotatii foarte mari. O inspectie mai detaliata a evolutiei randamentelor zilnice este realizata cu ajutorul urmatoarelor grafice:

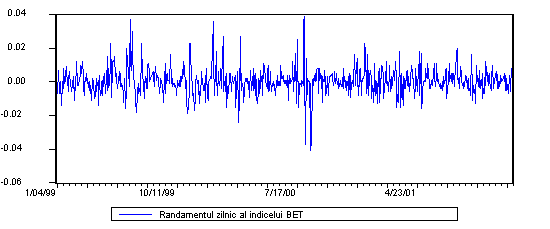
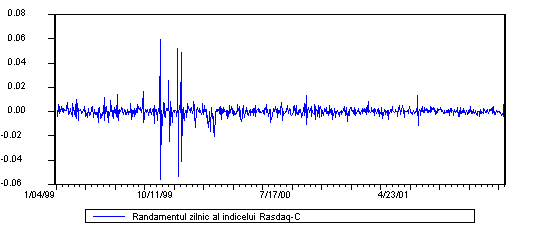
Figura 1: Evolutia Randamentelor Zilnice

Intr-adevar, pe piata extrabursiera si pe cea valutara a existat o nervozitate extrema in anumite perioade. Pentru piata valutara aceasta nervozitate este evidenta in prima parte a anului 1999. Pe piata Rasdaq, s-au consemnat cateva valori extreme la finele anului 1999. Mai precis, pe data de 8 septembrie 1999, indicele Rasdq-C a "sarit" cu peste 100 de puncte pentru ca in urmatoarea zi sa revina la trendul normal al perioadei. Pe 28 octombrie 1999 indicele sare cu aproape 100 de puncte, urmatoarea zi insemnand din nou una "normala".  Pe 29 septembrie 1999, inregistram din nou un salt foarte mare al indicelui cu circa 50 de puncte. Desigur ca aceste variatii extreme au facut ca piata extrabursiera in ansamblul ei sa fie extrem de volatila la finele anului 1999.

Daca pentru piata valutara si cea extrabursiera, in afara momentelor cu volatilitate ridicata mentionate, randamentele sunt relativ uniform dispersate, nu acelasi lucru putem sa spunem despre evolutia randamentului indicelui BET. Volatilitatea pare mai ridicata. Acest lucru este evidentiat de valoarea deviatiei standard (pentru BET valoarea fiind cea mai mare-vezi tabelul 1).

Evolutia randamentelor portofoliului creat este surprinsa de urmatorul grafic:

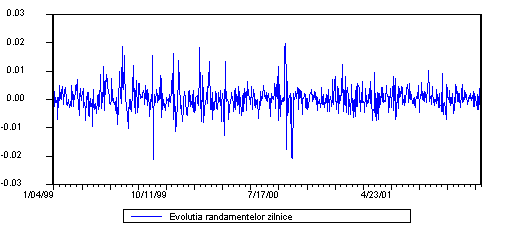
Figura 2: Evolutia Randamentelor Zilnice ale Portofoliului

Purtand amprenta evolutiei randamentelor indicelui BET, randamentele portofoliului creat par a nu avea o evolutie uniforma. Mai precis, perioadele cu volatilitate mai redusa alterneaza cu perioadele cu volatilitate mai ridicata. Dispersia seriei pare a nu fi constanta de-a lungul perioadei si de aceea avem un prim indiciu al heteroschedasticitatii. In particular, seria pare a fi mai volatila spre sfarsitul anului 1999 si in vara anului 2000. Spre sfarsitul intervalului de timp analizat, respectiv sfarsitul anului 2001, randamentele par a fi uniformizate. O informatie suplimentara asupra randamentelor portofoliului construit este data de graficul distributiei cumulative (vezi figura 3). Observam ca marea parte a randamentelor sunt plasate intre -0.01 si 0.01. Totusi exista extremitati pronuntate atat la stanga cat si la dreapta, inca un indiciu al faptului ca seria nu este normal distribuita si o indicatie a posibilei semnaturi "ARCH".

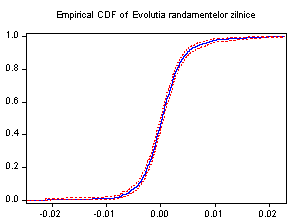
Figura 3: Distributia Cumulativa a Randamentelor Zilnice

Analiza grafica este foarte utila in descrierea seriilor si fenomenelor economice. Totusi, pentru certitudinea analizei, testele statistice sunt mult mai indicate. Vom testa prezenta semnaturii ARCH cu ajutorul corelogramei radicalului randamentelor zilnice. Sa notam ca numarul de lag-uri utilizate este 15. In coloana notata AC remarcam coeficientii de corelatie seriala, in timp ce in ultima coloana avem probabilitatea de acceptare a ipotezei "nu exista efecte ARCH" (aceasta fiind de fapt ipoteza nula). Coeficientii de autocorelatie nu inregistreaza valori prea mari. Ei isi modifica semnul la a cincea linie (respectiv al cincilea lag), marcand trecerea catre corelatie seriala negativa. Remarcam ca autocorelatia de lag 1 este pozitiva. In acelasi timp, valoarea probabilitii ipotezei nule este 0 pe toate cele 4 pozitii, indicand ca putem respinge ipoteza nula si furnizand informatia ca exista efecte ARCH. Din corelograma mai remarcam declinarea in timp a coeficientilor corelatiei pozitive, in timp ce coeficientii corelatiei negative inregistreaza cresteri si scaderi de succesive ale valorilor.

Tab. 2: Corelograma radicalului randamentelor

V.I. Depistarea Ecuatiei Volatilitatii

In aceasta etapa vom incerca sa depistam ecuatia care descrie cel mai bine volatilitatea portofoliului sau cu alte cuvinte riscul de portofoliu. O prima incercare este sa cautam un model standard GARCH(1,1). Rezultatele sunt prezentate in atasamentul studiului. Observam ca ambii termeni ARCH(1) si GARCH(1) au o influenta semnificativa din punct de vedere statistic asupra dispersiei seriei la un nivel de probabilitate mai ridicat de 5%. Ecuatia dispersiei ne arata variabila dependenta (respectiv portofoliul), metoda utilizata (ML-ARCH), numarul de observatii (759) precum si faptul ca a fost necesara numai o singura iteratie pentru a se atinge convergenta dorita. In acelasi timp avem coeficientii efectelor ARCH, GARCH si termenul constant. Termenul eroare testul z, precum si probabilitatea atasata acestuia din urma completeaza tabelul ecuatiei.

Totusi, analiza corelogramei radicalului reziduurilor standardizate arata ca ecuatia GARCH (1,1) nu este cea mai indicata. Intr-adevar, aceste reziduuri standardizate sunt puternic autocorelate.

Pornind de la ecuatia GARCH (1,1), au fost realizate incercari succesive de gasire a ecuatiei dorite. In final, modelul standard sau clasic GARCH (1,1) a fost abandonat si modelul asimetric EGARCH (1,1) a fost adoptat.Acest model prezinta un avantaj particular prin faptul ca nu este unul linear. Asa cum s-a prezentat la sectia de motivatie a modelelor GARCH (sectia III), pentru modelarea volatilitatii se considera in fapt logaritmul dispersiei mai degraba decat dispersia. De asemenea reziduurile sunt standardizate in interiorul modelului ceea ce prezinta un mare avantaj.

Ecuatia care modeleaza cel mai bine volatilitatea portofoliului construit este:

Observam ca efectul ARCH (in ecuatie coeficientul a) si GARCH sunt semnificative din punct de vedere statistic. Totusi ecuatia ne indica faptul ca nu exista un efect de levier. Coeficientul g este pozitiv si in plus nu este semnificativ din punct de vedere statistic. Deci efectul de asimetrie nu este evident. Remarcam insa succesul unui model GARCH non-linear in modelarea volatilitatii portofoliului nostru.

Pentru a valida aceasta ecuatie trebuie sa recurgem la teste aplicate termenilor reziduali. Asa cum s-a precizat la sectia de metodologie, vom face analiza corelogramei radicalului reziduurilor standardizate, precum si un test rezidual ARCH-LM.

Corelograma este urmatoarea:

Corelograma indica faptul ca termenii reziduali nu sunt autocorelati. Mentionam ca daca valoarea probabilitatii este mai ridicata de 0.05 putem accepta ipoteza nula "nu exista efecte ARCH reziduale". Observam in ultima coloana a tabelului ca acest lucru este valabil pentru toti cei 15 termeni. Pentru a intari cele spuse, vom aplica si un test ARCH-LM:

Din nou, valoarea probabilitatii trebuie sa fie mai mare decat 0.05 pentru a ne asigura ca nu exista efecte reziduale asupra dispersiei seriei. Valoarea de 0.73 ne indica inca o data ca nu exista efecte ARCH reziduale.

Vom completa analiza termenilor reziduali cu testul White pentru a verifica urmele de heteroschedasticitate. Pentru a ne asigura ca nu mai exista efecte de heteroschedasticitate (sau efecte GARCH) reziduale din nou valoarea probabilitatii trebuie sa fie mai mare de 0.05. In acest caz coeficientul vizat este STD_REZID^2(-1). Valoarea probabilitatii pentru acest coeficient de 0.61 indica faptul ca putem accepta ipoteza nula "nu exista efecte GARCH reziduale".

In concluzie modelul EGARCH (1,1) aplicat este cel indicat pentru a modela volatilitatea portofoliului. Cele 3 teste pentru termenii reziduali prezentate mai sus intaresc validitatea modelului propus.

VI.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p;  Descrierea Volatilitatii Portofoliului

Pana in acest punct atentia a fost concenrata spre depistarea celui mai indicat model de explicare a comportamentului dispersiei portofoliului nostru. Am vazut astfel ca setul de informatie din trecut are impact semnificativ asupra randamentelor prezente. Mai mult, am demonstrat faptul ca dispersia portofoliului nu are o evolutie constanta de-a lungul seriei, ci una oscilanta, avand o puternica amprenta asupra volatilitatii.

Desigur aceste aspecte tehnice sunt deosebit de importante pentru econometricieni si le ofera informatii utile asupra comportamentului volatilitatii. Dar un investitor individual este mai mult interesat in explicarea cauzelor ce au determinat ca anumite perioade de timp sa fie mai riscante decat altele. El ar dori sa stie de exempu daca exista o evolutie sezoniera a randamentelor sau nu. Daca anumite cauze se repeta in afectarea evolutiei pietelor de capital.

In cele ce urmeaza, ne vom focaliza atentia pe 2 aspecte:

1. depistarea momentelor de volatilitate ridicata si analiza lor;
2. discutarea a 2 evenimente cu impact presupus puternic, respectiv alegerile electorale din toamna anului 200 din Romania si atacurile teroriste asupra Statelor Unite din septembrie 2001.

VI.I. Prezentarea Volatilitatii Portofoliului

Aceasta este surprinsa din graficul urmator. Mentionam ca graficul este construit in baza ecuatiei EGARCH(1,1) descrisa mai sus.

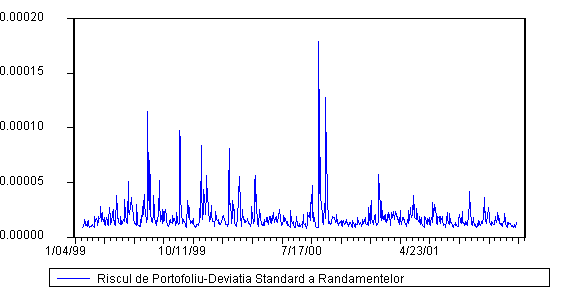
Figura 4: Volatilitatea Portofoliului

O privire la graficul de mai sus indica in mod clar faptul ca pe parcursul celor 3 ani, exista perioade mult mai volatile decat altele. Daca este sa facem o analiza pe ani, volatilitatea cea mai pronuntata se remarca in anul 1999, unde sunt cele mai numeroase "varfuri". Volatilitatea anului 2000 ar fi putut avea o amplitudine asemanatoare cu cea inregistrata in anul 2001 daca nu ar fi existat "varful" inregistrat in luna august a acestui an. O investigare a randamentelor zilnice a celor 3 portofolii initiale care au condus la constructia portofoliului nostru ofera dovada faptului ca volatilitatea in luna august a anului 2000 este pusa pe seama evolutiei pietei bursiere. Figura 1 indica faptul ca evolutia dolarului si a pietei Radaq a fost relativ calma. "Socul" produs pe piata bursiera este evidentiat cu ajutorul urmatorului grafic:

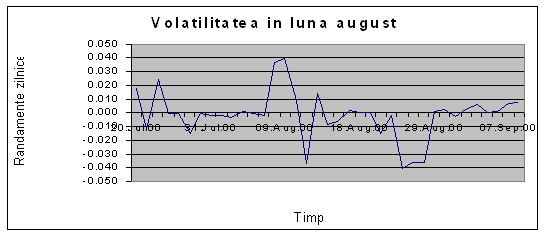
Figura 5: Evolutia Indicelui BET in Perioada 20 Iulie 200-10 Septembrie 2000

In graficul de mai sus, desi ne intereseaza in primul rand luna august, am inclus ultimele 10 zile ale lunii iulie si primele 10 zile ale lunii septembrie (zile calendaristice) pentru a evidentia mai bine socurile petrecute in luna august pe piata bursiera. Putem explica asadar cel mai inalt varf de volatilitate a portofoliului nostru cu ajutorul graficului 5. Daca in ziua de 9 august 2000, randamentul indicelui BET era de 0.039, acesta ajunge extrem de rapid (respectiv la data de 11 august 2000) la o valoare extrem de redusa, respectiv -0.037 (aceasta fiind o zi de vineri). In ziua de luni (14 august 2000), BET recupereaza substantial randamentul pierdut in ziua de vineri, ajungand la 0.014. Daca luam in considerare studiile realizate pe alte piete bursiere, acest lucru observat pare surprinzator. Mentionam ca in anumite studii (vezi French, 1980), in care se analizeaza efectul de weekend, se dovedeste faptul ca, in general, randamentele tind sa creasca catre sfarsitul saptamanii, urmand ca in prima zi de tranzactionare a saptamanii (respectiv luni) sa inceapa cu o usoara corectie negativa a cotatiilor si in consecinta cu o oarecare diminuare a randamentelor.

Totusi, nu se poate afirma ca la BVB, ziua de luni ofera randamente in crestere si cea de vineri o reducere a lor . De exemplu, spre sfarsitul lunii august, unde avem din nou o perioada cu volatilitate accentuata, declinul in randamentele zilnice se produce incepand cu data de miercuri 23 august 2000. Intr-o zi, randamentul zilnic al indicelui BET ajunge de la -0.001 la -0.041. Ziua de luni, 28 august 2000 gaseste randamentul indicelui BET la aceeasi valoare ca in ziua de vineri 25 august 2000, respectiv -0.036. Ziua de 29 august reprezinta evident o zi mult mai buna, randamentul urcand pana la 0.001.

Asa cum s-a mentionat mai sus, cel mai riscant an pentru portofoliul nostru este anul 1999. Varfurile de volatilitate inregistrate (vezi graficul 4) sunt datorate activitatii celor 3 piete. Daca analizam din nou graficul 1 observam ca in 1999 atat piata extrabursiera, cat si dolarul american au avut cele mai agitate perioade in cadrul intervalului de timp analizat (vezi pagina 9 a acestui studiu pentru mai multe detalii). De asemenea indicele BET a cunoscut anumite perioade in acest an destul de volatile. Observam ca lunile ianuarie si februarie inregistreaza o volatilitate redusa, purtand in mod evident amprenta calmului normal inregistrat pe Bursa de Valori Bucuresti in aceasta perioada. Din luna martie apar valori mari repetate ale deviatiei standard (plasate in jurul valorii de 0.00010). Aceasta se datoreaza socului produs pe piata valutara. De asemenea pe bursa incep perioadele in care se estimeaza sau se anunta profiturile si/sau dividendele inregistrate de companiile cotate. Perioadele cu volatilitate ridicata alterneaza totusi cu perioade mai "calme" pentru portofoliul ales. Aceasta se explica partial prin vacantele normale care se inregistreaza pe BVB. O alta cauza o reprezinta fluctuatiile reduse ale randamentelor zilnice ale indicelui Rasdaq-C si a cursului monedei americane (cu exceptiile notate deja). Impreuna, indicele Rasdaq-C si dolarul american, reprezentand 50% din portofoliul construit, reusesc sa reduca fluctuatiile clar mai mari inregistrate de indicele BET. Aceasta este inca o dovada a posibilitatii reducerii riscului unui portofoliu prin diversificare.

Anul 2001 s-a caracterizat printr-o volatilitate relativ redusa a portofoliului (daca este sa o comparam cu cea a anului 1999). Daca in anul 1999 deviatia standard deseori era situata in jurul valorii de 0.00010, in anul 2000 aceasta ajunge sau depaseste rareori valoarea de 0.00005. Explicatia poate fi oferita de graficul 1. Piata Rasdaq-C si cea valutara (respectiv evolutia dolarului american) cunosc fluctuatii reduse ale randamentelor zilnice. De asemenea, evolutia randamentului indicelui BET in acest an este mult mai stabila, respectiv fluctuatiile sunt mult mai reduse. Efectul de diversificare actioneaza cu succes in acest an ducand la reducerea substantiala a riscului de portofoliu.

Impactul alegerilor generale din Romania din noiembrie 2000 asupra portofoliului

Este cunoscut faptul ca anumite evenimente (in econometrie denumite uneori "socuri" sau "inovatii") au un anumit impact asupra investitiilor financiare. Nu de putine ori pe pietele financiare romanesti s-a observat faptul ca anumite fenomene globale nu influenteaza prea mult piata. In acest studiu vom verifica empiric acest fapt prin studiul impactului alegerilor generale din Romania din noiembrie 2000 si a atacurilor teroriste asupra Statelor Unite din septembrie 2001(care au afectat profund pietele bursiere din lume) asupra portofoliului nostru.

Pentru a analiza impactul alegerilor generale din Romania din noiembrie 2000 vom folosi o perioada ante-eveniment si o perioada post-eveniment . Vom considera perioada ante-eveniment luna octombrie 2000 precum si luna noiembrie pana in prima zi electorala. Perioada eveniment o reprezinta intreaga perioada a celor 2 scrutine (inclusiv cu pauza dintre ele), iar perioada post-eveniment este cuprinsa intre prima zi dupa terminarea celui de-al doilea scrutin si 15 decembrie 2000.

Figura 6 reda evolutia randamentelor zilnice ale portofoliului in perioada de timp aleasa. Observam cum perioada ante-eveniment si cea eveniment au practic acelasi continut, respectiv evolutia randamentelor zilnice ale portofoliului este asemanatoare, ceea ce reprezinta in mod normal un rezultat surprinzator. Ceea ce ar reprezenta un eveniment cu impact semnificativ asupra pietelor si a economiei nationale in ansamblul ei, alegerile generale din Romania au lasat "indiferente" pietele financiare din Romania. Putem explica acest rezultat fie prin indiferenta pietelor financiare din Romania la astfel de evenimente ca fenomen general, fie prin faptul ca sondajele de opinie dadeau in perioada ante-eveniment drept castigator actualul partid de guvernamant.

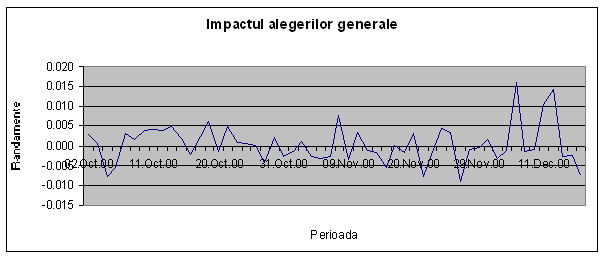
Figura 6: Impactul Alegerilor Generale din Noiembrie 2000 Asupra Volatilitatii Portofoliului

Ceea ce este interesant de notat este faptul ca volatilitatea portofoliului este ridicata incepand cu 5 decembrie 2000. Pe 5 decembrie, randamentul este -0.001, pe 6 decembrie ajunge la 0.016, iar pe 7 decembrie coboara la -0.002. Cu siguranta acesta este un soc puternic, dar consideram ca nu se datoreaza alegerilor generale care se incheiasera deja si se stia castigatorul atat in Parlament cat si la presedintie.

Impactul atacurilor teroriste petrecute in Statele Unite in septembrie 2001 asupra portofoliului

Acesta reprezinta cu siguranta un eveniment global cu efecte majore asupra burselor si pietelor financiare din intreaga lume. Vom analiza in ce masura acest fenomen a afectat portofoliul construit in acest studiu. Analiza prezinta importanta datorita faptului ca nu putini analisti remarca izolarea pietelor financiare din Romania si gradul redus de integrare al acestor piete in pietele financiare internationale.

Vom considera perioada ante-eveniment a doua jumatate a lunii august a anului 2001 pana pe data de 10 septembrie (inclusiv), vom lasa perioada eveniment sa fie compusa din 5 zile de tranzactionare (respectiv 11 septembrie-17 septembrie). Perioada post-eveniment este considerata perioada cuprinsa intre 18 septembrie 2001 si 28 septembrie 2001, perioada considerata ca fiind suficienta pentru a incorpora efectele impactului in cotatiile de pe pietele financiare considerate.

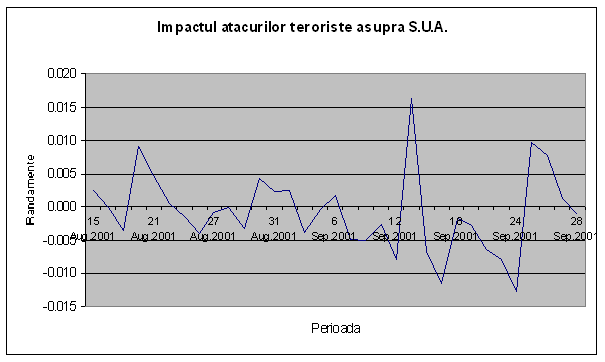
Figura 7 ne indica evolutia randamentelor zilnice in toata aceasta perioada.

Figura 7: Impactul Atacurilor Teroriste din S.U.A.Asupra Volatilitatii

Un asemenea eveniment surpriza pare sa fi avut un impact asupra portofoliului nostru. Daca ne uitam la graficul de mai sus, observam in mod clar o crestere a volatilitatii portofoliului atat in perioada eveniment, cat si in perioada post-eveniment (raportat la perioada ante-eveniment). Din punct de vedere al amploarei (al magnitudinii) socul este evident. Sensul in care a actionat este totusi surprinzator. Mai intai sa precizam faptul ca adevaratul soc se produce din data de 13 septembrie 2001 (deci cu o zi intarziere). Putem sa afirmam acest lucru din moment ce in data de 12 septembrie nu se intampla nimic spectaculos. In data de 13 septembrie randamentul portofoliului urca de la -0.008 (ziua precedenta) la 0.016, ceea ce reprezinta un salt mai mult decat spectaculos. Mai mult, aceasta modificare pozitiva a randamentelor se inregistra pe toate cele 3 piete considerate. In ciuda unui fenomen global deosebit de negativ, portofoliul castiga randamente!

In zilele urmatoare ale saptamanii, lucrurile "intra in normal", adica portofoliul incepe sa piarda din randamente. Dar din nou, in mod ciudat, din data de 24 septembrie 2001, cand pietele financiare de pe mapamond cunosteau caderi spectaculoase, portofoliul incepe din nou "sa se miste in sus".

Putem concluziona prin a remarca faptul ca in mod clar ceva s-a produs pe pietele financiare din Romania incepand cu 12 septembrie 2001. Volatilitatea este substantial diferita decat cea din perioada ante-eveniment. Dar evolutia randamentelor portofoliului construit este surprinzatoare in sensul ca a cunoscut perioade foarte scurte de timp (zile) cand in loc sa cunoasca un declin semnificativ, au avut un trend crescator.

VII.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   Concluzii

In acest studiu a fost realizata o analiza a riscului de portofoliu prin utilizarea unor instrumente deosebit de moderne si utile, respectiv modelele GARCH. S-a lucrat cu un interval de timp de 3 ani, luand in considerare piata bursiera, piata extra-bursiera si evolutia dolarului american. In acest sens, s-a construit un portofoliu ipotetic care sa ia in considerare cele 3 piete. Modelele GARCH s-au dovedit extrem de utile in modelarea riscului de portofoliu, respetiv a volatilitatii. Dupa incercari repetate cel mai bun model s-a dovedit a fi modelul asimetric E-GARCH (1,1), care a inclus in ecuatia mediei si termenii ARMA (in cazul nostru de lag 12). In acest fel s-a produs o corectie de succes atat a corelatiei seriale a randamentelor reziduale, cat si a heteroschedasticitatii. S-a demonstrat in acelasi timp ca impactul "inovatiilor recente" (cu alte cuvinte a stirilor, evenimentelor care duc la modificarea cotatiilor in piata este unul exponential si nu linear, cum este descris de econometria "clasica").

In partea urmatoare a studiului de caz, am realizat o analiza a volatilitatii portofoliului. Am demonstrat ca efectul de diversificare este extrem de important in cazul realizarii de investitii financiare. Rezultatele cuprinse in tabelul 1 sunt edificatoare in acest sens. Riscul, masurat prin deviatia standard, a fost redus surprinzator. De asemenea asimetria a fost redusa si ea simtitor.

Evolutia deviatiei standard (asa cum a rezultat dupa aplicarea modelului EGARCH (1,1)) a fost diferita pe ani. Volatilitatea a fost cea mai ridicata in anul 1999 si cea mai redusa in anul 2001. Totusi, cel mai ridicat "varf de volatilitate" se inregistreaza in anul 2000 datorita unor evenimente petrecute pe Bursa de Valori Bucuresti.

Alegerile generale din Romania din noiembrie 2000 nu au perturbat pietele financiare din Romania asa cum ar fi fost normal, data fiind amplitudinea unui asemenea eveniment. In ceea ce priveste fenomenele teroriste asupra Statelor Unite din septembrie 2001, acestea au avut un impact notabil asupra portofoliului. Acest impact a fost unul surprinzator. Respectiv, in data de 13 septembrie, cand in mod normal pietele trebuiau sa fie in cadere, toate cele 3 piete analizate aveau randamente pozitive. Faptul ca pietele financiare din Romania nu reactioneaza prompt la socuri foarte puternice (asa cum sunt cele 2 evenimente analizate) reprezinta un element de nesiguranta pentru investitor, in sensul ca este destul de dificil de gestionat riscul unui portofoliu in asemenea situatii. Ca atare, el poate recurge la un efect care actioneaza in permanenta si demonstrat in acest studiu: efectul de diversificare.

Atasament

Rezultatele Modelului GARCH (1,1)

Ecuatia GARCH (1,1)

Corelograma Radicalului Randamentelor Standardizate

Bibliografie:

1.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Bollerslev, Tim (1986), "Generalized Autoregressive Conditional Heteroskedasticity", Journal of Econometrics, vol. 31, pag. 81-87

2.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Campbell, John Y., Lo, Andrew W. si Mackinley, Craig A. (1997), "The Econometrics of Financial Markets", Ed. Princeton University Press, pag. 479-490

3.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Darasteanu, Catalin Cristian (2002), "Testing CAPM for stocks trade dat Bucharest Stock Exchange", Pagina Pietei de Capital din Romania (www.kmarket.ro)

4.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Engle, Robert, Nelson, D. si Bollerslev, Tim (1994), "ARCH models", Handbook of Econometrics, Ed. R. Engle and McFadden, pag. 2959-3038

5.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Fama, Eugene F., Fischer, Lawrence, Jensen, Michael C. si Roll, Richard (1969), "The adjustment of stock prices to new information", International Economic Review, vol. 10, nr. 1, pag. 1-21

6.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; French, Keneth R. (1980), "Stock returns and the weekend effect", Journal of Financial Economics, vol. 8, pag. 55-69

7.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Todea, Alexandru (2001), "Caracterul instabil al riscului de piata evidentiat empiric pe piata romaneasca", Pagina Pietei de Capital din Romania (www.kmarket.ro)

8.   &nbs 15515s1818p p;   &nbs 15515s1818p p;   &nbs 15515s1818p p; Surse Internet:

www.bnro.ro, site oficial al Bancii Nationale din Romania

www.bvb.ro, site oficial al Bursei de Valori Bucuresti

www.kmarket.ro, site al Paginii Pietei de Capital din Romania