Interactiunea fluid-fluid

Interactiunea fluid-fluid

11.1. Faze de interfata

Cānd doua faze fluide sunt puse īn contact, īn absenta unor reactii chimice, sunt posibile trei situatii.

a. Īntre cele doua faze se produce un transfer nelimitat de masa, pāna la obtinerea unei singure faze. Este cazul fluidelor perfect miscibile. Exemple de fluide miscibile: gazele, produsele petroliere, apa si alcoolul etilic.

b. Īntre cele doua faze se produce un transfer de masa limitat, pāna la atingerea echilibrului de faza. Este cazul fluidelor partial miscibile. Īntre cele doua faze se pastreaza o suprafata aparenta de separatie. Exemple de fluide partial miscibile: titei si gaze, apa si gaze.

c. Īntre cele doua faze nu are loc transfer de masa, pastrāndu-se o suprafata aparenta de separatie. Este cazul fluidelor nemiscibile. Exemple de fluide nemiscibile: mercur si aer, titei si apa. Īn realitate, chiar si īntre fluidele foarte diferite, considerate nemiscibile, echilibrul de faza presupune un schimb de masa foarte limitat.

Īn zacamintele de hidrocarburi exista toate cele trei categorii de perechi de fluide: fie ca fluide de zacamānt, fie ca sisteme mixte, formate din fluidele de zacamānt si diverse fluide injectate. Injectia fluidelor se face, īn mod pre-dominant, pentru cresterea fractiei de hidrocarburi extrase īn cursul exploatarii zacamāntului.

Miscibilitatea fluidelor de zacamānt cu diferite fluide de injectie (gaze, gaze lichefiate, dioxid de carbon, solutii micelare) necesita o abordare larga si nu va fi tratata aici. Principiile generale ale dezlocuirii titeiului si a condensatului de catre fluide de injectie īn conditii de miscibilitate sunt prezentate īn anexa 2.

Celelalte doua categorii de fluide mentionate mai sus (partial miscibile si nemiscibile) vor fi tratate īmpreuna. Īn ambele cazuri, īntre ele apar suprafete aparente de separatie. Īn mod formal, tipurile de interfata fluid-fluid sunt: lichid - gaz si lichid - lichid. O interfata lichid - gaz particulara este cea dintre un lichid monocomponent si vaporii proprii.

Conditia generala pentru existenta unei interfete stabile īntre diferite faze este ca energia libera de formare a interfetei sa fie pozitiva, cu alte cuvinte, formarea interfetei presupune un consum de energie. Īn cazul īn care aceasta energie este nula sau negativa, orice perturbatie exterioara, concretizata printr-un aport de energie, va conduce la cresterea continua a regiunii de interfata, pāna la dispersia completa a unei faze īn cealalta. Această 727p155h ; comportare este specifica fluidelor miscibile si a celor nemiscibile care formeaza emulsii īn mod spontan.

Suprafata aparenta de separatie macroscopica dintre faze are un corespondent la scara microscopica, anume o faza de interfata. Faza de interfata este alcatuita din molecule sau ioni apartinānd ambelor faze volumice īn contact.

Grosimea fazei de interfata este variabila, īn functie de natura fazelor volumice si de concentrarea unor tipuri de molecule īn regiunea interfetei. La lichidele simple, faza de interfata cuprinde circa doua rānduri de molecule. La fluidele mai complexe, grosimea si consistenta fazei de interfata sunt mai mari.

Omogeneitatea fazelor volumice poate fi precizata de faptul ca marimile termodinamice sunt constante īn cuprinsul lor. Spre deosebire de fazele volumice, faza de interfata este neomogena, desi poate cuprinde o regiune omogena īn zona mediana. Īn figura 11.1 sunt prezentate cele doua situatii extreme: o inter- fata de grosime mare (fig. 11.1,a) si o interfata de grosime mica (fig. 11.1,b).

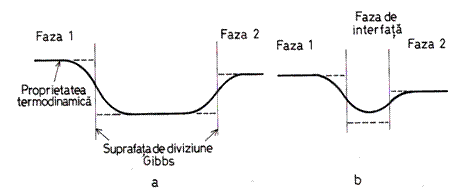
Fig.11.1 Ilustrarea fazelor de interfata [119].

Figura 11.1,a reprezinta o schematizare a profilului unei proprietati ter-modinamice (potential chimic, energie interna, entalpie etc.) cānd grosimea fazei de interfata este atāt de mica īncāt regiunile neomogene adiacente fazelor volumice se īntrepatrund.

Figura 11.1,b reprezinta aceeasi schematizare pentru cazul īn care se constituie o faza omogena, delimitata de cele doua zone neomogene adiacente fazelor volumice. Se poate observa ca zona omogena din faza de interfata este diferita de cele doua zone neomogene cāt si de fazele volumice prin proprietatile ei, derivate din compozitia diferita, dar si din interactiunea cu fazele volumice. De altfel, gradientul de compozitie din faza de interfata duce la existenta gradientilor tuturor proprietatilor termodinamice ale fazei de interfata.

Ţinānd seama de faza de interfata, orice sistem termodinamic format din doua faze volumice nemiscibile sau partial miscibile aflate īn contact se poate īnlocui cu un sistem echivalent format din doua faze volumice omogene si o faza de interfata.

Dupa Gibbs, care este un pionier īn acest domeniu, faza de interfata este o suprafata de diviziune geometrica, unica si fictiva, numita suprafata de separatie. Faza de interfata ca suprafata de separatie este un model idealizat, greu de comparat cu un sistem real (dupa Guggenheim, este mai usor sa folosesti teoria lui Gibbs decāt sa o īntelegi). Datorita simplitatii, modelul de suprafata a capatat o larga raspāndire, inclusiv īn ingineria de zacamānt. Un punct foarte slab al modelului este incapacitatea descrierii adsorbtiei unor substante la nivelul fazei de interfata. Nu se poate echivala adsorbtia unui component cu continutul real al componentului din unitatea de suprafata.

Īn cadrul studiului termodinamic al fazei de interfata ca faza de echilibru, ipoteza fundamentala de lucru este urmatoarea: faza de interfata este o faza neautonoma, īn sensul ca functiile termodinamice care caracterizeaza aceasta faza nu depind numai de functiile termodinamice proprii, ci si de functiile termodinamice ale fazelor volumice din care se formeaza.

Dezvoltarea teoriei lui Gibbs pe baza unor observatii experimentale a scos īn evidenta deosebiri apreciabile īntre marimi specifice suprafetei de separatie, masurate īn regim de echilibru si aceleasi marimi masurate īn regim dinamic, cānd fazele de interfata se afla īn regim de neechilibru [79]. Daca se are īn vedere ca īntr-o fractie de ordinul a 99% din volumul zacamāntului vitezele de miscare a fazelor sunt extrem de mici (ordinul de marime al vitezelor este cm/zi), a considera ca sistemul alcatuit din faze volumice separate de interfete este la echilibru reprezinta o ipoteza de lucru perfect valabila.

Un interes special īl prezinta cāmpul de forte din faza de interfata. Īntre moleculele, atomii si/sau ionii substantelor prezente īn cele doua faze volumice si, evident, īn faza de interfata se manifesta o serie īntreaga de forte cu raza mica de actiune, de ordinul a cāteva unitati Ängstrom (de legatura chimica) sau cu raza mare de actiune (electrostatice, de inductie, de dispersie si de rezonanta). Aceste forte sunt fie de atractie, fie de repulsie. Ele variaza invers proportional cu puterea a doua, pāna la puterea a saptea a razei (v. anexa 2).

Mai usor de intuit este situatia unui lichid īn echilibru cu vaporii proprii. Moleculele stratului superficial fiind mai putin atrase de moleculele de gaz decāt moleculele din lichid, din cauza pozitiei lor speciale, manifesta o tendinta de apropiere īntre ele mai mare decāt celelalte molecule. Ca urmare, energia potentiala a moleculelor din stratul superficial este mai mare decāt cea a moleculelor din interiorul lichidului. Aceeasi situatie se regaseste si īn cazul a doua faze oarecare.

11.2. Tensiunea interfaciala

Sa consideram un lichid monocomponent īn contact cu vaporii proprii, la echilibru. O crestere a ariei stratului superficial presupune transferul de molecule (atomi, ioni) din interiorul lichidului īntr-o zona cu energie potentiala superioara. Acest transfer necesita un consum de energie. Prin definitie, suplimentul de energie necesar pentru a creste aria suprafetei cu o unitate este tensiunea superficiala. Aceasta se se noteaza cu s si masoara īn J/m² sau, echivalent, īn N/m.

O alta modalitate de a privi marirea ariei stratului superficial este urmatoarea: apropierea excesiva a moleculelor duce la cresterea fortelor de repulsie, pe cānd departarea lor, īn anumite limite, duce la cresterea fortelor de atractie. Astfel, pentru a separa moleculele din stratul superficial pe un anumit contur trebuie aplicata o forta exterioara care sa īnvinga aceste forte de atractie dintre molecule. Din acest motiv, cresterea ariei suprafetei se poate face prin exercitarea unei forte īn planul suprafetei care va duce la departarea moleculelor si crearea spatiului necesar migrarii moleculelor din interior īn stratul superficial. Aceasta forta, uniform distribuita, raportata la perimetrul pe care ea se exercita are aceeasi valoare cu energia consumata raportata la aria creata. Este, deci, tensiunea superficiala. Īn consecinta, se poate scrie:

(11.1.)

si

(11.2)

īn care W, F, A, L sunt, respectiv, energia (lucrul mecanic), forta, aria si perimetrul.

Daca suprafata este curba, forta se exercita īn planul tangent la suprafata īn fiecare punct de pe perimetrul pe care actioneaza.

Īn legatura cu forma geometrica a suprafetei de separatie, din practica curenta se stie ca uneori este plana, alteori este curba. Se stie ca starea de echilibru a unui sistem este asociata cu o energie minima. Īn cazul de fata, energia de suprafata minima se traduce printr-o arie minima. Cum orice sistem tinde catre echilibru lichidul va avea tendinta de a avea o suprafata de arie minima īn raport cu volumul lui. Forma sferica asigura raportul minim arie/volum. Pe de alta parte, datorita fortei gravitationale, conditia de energie potentiala minima se traduce printr-o pozitie cāt mai coborāta a centrului de greutate. Forma suprafetei, īn absenta altor forte exterioare, va fi determinata de echilibrul dintre cele doua tendinte: arie minima si cota minima a centrului de greutate. Pentru a īntelege mai bine, sa imaginam urmatorul experiment: īntr-un vas de dimensiuni mari asezam o picatura foarte mica de mercur. Aceasta va fi aproape sferica. Datorita masei mici, energia potentiala este mica, mult mai mica decāt energia superficiala. Daca, īn continuare, alimentam aceasta picatura marindu-i dimensiunile, vom constata abateri din ce īn ce mai mari de la forma sferica. Atunci cānd volumul de mercur va fi comparabil cu volumul vasului, acesta va forma o suprafata plana, ca orice lichid aflat īn spatii largi, īn cantitati apreciabile.

Tensiunile superficiale ale unor lichide date, īn conditii date, reprezinta niste constante, fiind caracteristici moleculare, spre deosebire de tensiunile mecanice care cresc proportional cu deformarea (legea lui Hooke). Īn regim dinamic, apar variatii ale tensiunii superficiale, datorita histerezei de rearanjare a moleculelor din interfata īn pozitia de echilibru. Cu alte cuvinte, la modificarea ariei sau formei interfetei, are loc o rearanjare a moleculelor pāna la atingerea echilibrului de forte īn regiunea de suprafata. Īn acest interval de timp, de ordinul milisecundelor, tensiunea superficiala scade cu o anumita valoare.

Consideratiile de mai sus se pot generaliza īn īntregul lor si pentru interfata unui lichid cu un gaz oarecare sau pentru interfata dintre doua lichide. Astfel, tensiunea superficiala poate fi tratata ca un caz particular de tensiune interfaciala. Diferenta este data numai de nivelul fortelor intermoleculare care genereaza un cāmp de forte specific fiecarei perechi de fluide.

Fortele intermoleculare care determina energia libera de suprafata, adica tensiunea interfaciala, sunt aceleasi care determina caldura latenta si fierberea. Asa cum este de asteptat, solidele, īn special metalele, care au o temperatura de fierbere mare, au si o energie libera de suprafata mare (s > 1000 mJ/m²). Din contra, cu cāt temperatura de fierbere este mai mica, energia libera de suprafata (tensiunea superficiala) este mai mica. Cāteva exemple: mercurul T_f = 357 ⁰C si s = 485 mJ/m²; apa T_f = 100 ⁰C si s 73 mJ/m²; argonul T_f = −186 ⁰C si s 13,2 mJ/m²; hidrogenul T_f = −253 ⁰C si s = 2,3 mJ/m².

Īn tabela 11.1 sunt date cāteva valori pentru tensiunile superficiale ale unor hidrocarburi si tensiunile interfaciale dintre aceste hidrocarburi si apa la presiune atmosferica si temperatura de 23 ⁰C.

Tabela 11.1. Tensiunile superficiale ale alcanilor si tensiunile interfaciale īntre alcani si apa.

Pentru normal-alcani, la temperatura de 20⁰ C, Wiener (citat īn [88]), a stabilit urmatoarea formula empirica de evaluare a tensiunii superficiale:

(11.3.)

īn care n este numarul de atomi de carbon din molecula, iar s rezulta īn mN∙m.

Tensiunea interficiala titei - gaze, condensat - gaze si apa - gaze īn conditii de zacamānt este specifica fiecareia dintre cele trei sisteme si depinde de compozitia fazelor, si de temperatura. Dependenta de presiune este mai mult implicita, īn sensul ca presiunea influenteaza procesul de schimb de masa īntre lichid si gaze si, īn consecinta, compozitia fazelor. Īn volumul I al acestei lucrari [44, p.190,230], sunt prezentate tensiunile interfaiciale titei - gaze si condensat - gaze. O mentiune speciala este aceea ca īn apropierea punctului critic compozitia fazelor devine foarte apropiata si, īn consecinta, tensiunea interfaciala devine foarte scazuta, ca īn punctul critic sa se anuleze. Īn cazul titeiurilor, pe parcursul exploatarii zacamāntului, tensiunea interfaciala titei-gaze creste, īn general, cu un ordin zecimal de marime fata de cea corespunzatoare presiunii de saturatie [113]

Date referitoare la tensiunea superficiala a apei īn conditii de zacamānt sunt putine. La presiunea atmosferica aceasta variaza de la 74,75 mN/m la 5⁰C la 62,3 mN/m la 80⁰C. Tensiunea superficiala a solutiilor de NaCl la 20⁰C variaza īntre 72,53 mN/m pentru apa distilata la 81 mN/m la concentratia de 90 g/l.

Tensiunea interfaciala apa-titei depinde de compozitia chimica a titeiului, de prezenta tensidelor, de ratia de gaze īn solutie, de pH-ul apei, de presiune si de temperatura. Valorile sale sunt de ordinul a 5 - 35 mN/m, īn conditii de zacamānt.

Influenta temperaturii asupra tensiunii interfaciale apa-titei pentru trei titeiuri este prezentata īn figura 11.2.

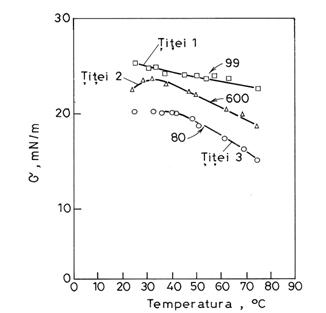
Fig.11.2. Influenta temperaturii asupra tensiunii interfaciale apa-titei

(cifrele de pe curbe reprezinta vāscozitatea titeiului īn mPa∙s).

O influenta majora asupra tensiunii interfaciale apa - titei o are prezenta tensidelor (denumite si agenti activi de suprafata, substante tensioactive, surfactanti, detergenti). Aceste substante micsoreaza tensiunea interfaciala apa - titei cu pāna la cāteva ordine zecimale de marime. Pentru a explica acest lucru, trebuie amintit ca substantele tensioactive au o molecula de un tip special, īn sensul ca au o parte polara si una de forma unei catene hidrocarbonice. Partea polara a moleculei este solubila īn apa si tinde sa transfere molecula īn aceasta faza. Din contra, cealalta parte este solubila īn titei si tinde sa transfere īntreaga molecula īn titei. Īn functie de echilibrul celor doua tendinte, molecula se dizolva īntr-una din cele doua faze. Spre exemplu, un sulfonat (fig. 11.3.) cu un lant care contine mai putin de 12 atomi de carbon, este solubil īn apa, pe cānd un sulfonat cu un lant care contine mai mult de 14 atomi de carbon este solubil īn titei.

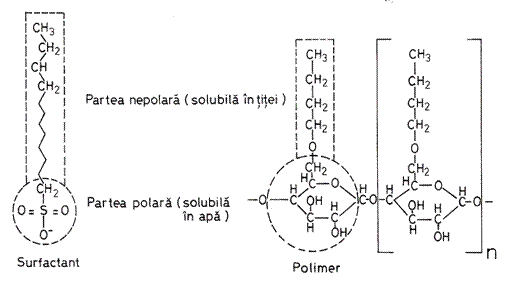
Fig. 11.3. Structura moleculelor de surfactanti.

Indiferent de solubilitatea īn cele doua faze, datorita faptului ca se afla la limita de solubilitate, moleculele acestor substante se concentreaza la suprafata de separatie, mai precis īn faza de interfata īn apropierea fazei de interfata, ceea ce duce la diminuarea gradientului de compozitie si, implicit, la scaderea contrastului dintre fortele intermoleculare din fazele volumice.

Solubilitatea tensidelor mai este influentata de compozitia titeiului, de concentratia lor (scade cu cresterea concentratiei) si de mineralizatia apei (o concentratie mare īn ioni scade solubilitatea tensidelor īn apa), dar si de natura ionilor prezenti īn apa.

Īn figura 11.4. este aratata influenta concentratiei īn tenside asupra tensiunii interfaciale si mecanismul molecular care determina o astfel de influenta. Se poate constata ca exista o concentratie optima, care determina o tensiune interfaciala minima. Concentratia optima corespunde unei concentratii maxime īn faza de interfata.

Comportarea tensidelor depinde mult de structura lor, ca si de compozitia titeiului. Problema este mult prea complexa pentru a fi prezentata aici. Exista o literatura foarte bogata pe aceasta tema datorita aplicabilitatii practice īn domeniul cresterii factorului de extractie a titeiului din zacaminte. Una din sintezele cele mai importante este cea a lui Donaldson [88]. Determinarea tensiunii interfaciale se face printr-un numar mare de metode. Descrierea cea mai detaliata a acestor metode este facuta de Adamson [90]. Dintre acestea amintim: metoda picaturii suspendate (stalagmometria), metoda ascensiunii capilare, metoda balantei Wilhelmy, metoda picaturii rotitoare.

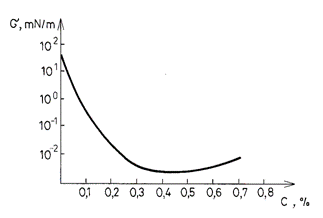
Fig. 11.4. Influenta concentratiei īn tenside

asupra tensiunii interfaciale apa-titei [88].

Metoda folosita depinde si de valoarea tensiunii interfaciale. Spre exemplu, pentru tensiunile interfaciale ultrascazute (īn prezenta tensidelor) se recomanda metoda stalagmometrica si metoda picaturii rotitoare.

La determinarea tensiunii interfaciale trebuie atins echilibrul dintre faze.

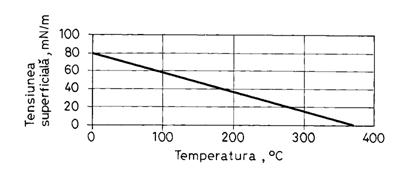
Se dau valorile tensiunii superficiale a apei īn functie de temperatura la presiunea de vapori īn tabelul de mai jos. Sa se estimeze temperatura critica a apei si entropia superficiala.

Raspuns.

Daca se reprezinta grafic perechile de valori tensiune superficiala - temperatura la presiunea de vapori (vezi figura) se constata ca aceasta scade aproximativ liniar.

Ținānd seama de faptul ca la punctul critic tensiunea superficiala se anuleaza, prin extrapolarea dreptei din grafic se obtine 370 ⁰C. Valoarea reala este de 374,12 ⁰C. Diferenta nu este foarte mare.

Entropia superficiala este definita prin relatia: ∂T, ceea ce reprezinta panta dreptei din figura. Calculānd, rezulta =0,23 J/m²∙K.

Aplicatia 2.

Sa se determine cantitatea de energie care se elibereaza prin contopirea moleculelor mici de apa cu raza r₁ = 2 m īntr-o picatura cu raza de 200 m la temperature de 20⁰C.

Raspuns.

Energia eliberata se datoreaza scaderii ariei suprafetei libere a apei: īn care W este energia eliberata, A variatia suprafetei libere iar temsiunea superficiala a apei la 20⁰C (72,75 mN/m),

Numarul de picaturi intrate īn coalescenta este:

Scaderea ariei va fi:

Rezulta:

Īn ipoteza lipsei schimbului de caldura cu exteriorul, cresterea de temperatura a apei va fi de cca 40⁰C.

Aplicatia 3.

sin sin Se neglijeaza efectul cāmpului gravitational.

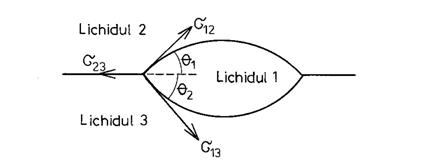
Raspuns.

La echilibru, presiunea īn sistem este aceeasi (legea lui Pascal). Asta īnsemneaza ca presiunea pe cele doua interfete este constante si, deci, curbura este aceeasi. Conform legii lui Laplace, daca interfetele superioara si inferioara au razele de curbura R₁ si, respective R₂, este valabila relatia:

Daca se obtine imediat rezultatul cautat: componentele verticale ale tensiunii interfaciale sunt egale, dupa cum era de asteptat.

11.3. Diferenta capilara de presiune

Consecinta cea mai importanta a existentei tensiunii interfaciale este diferenta capilara de presiune. Īn principiu, aceasta indica faptul ca de o parte si de alta a unei interfete curbe presiunea este diferita. Interfetele fiind īntegral curbe īn spatii īnguste, denumite capilare, acestei diferente de presiune i se adauga atributul de capilara. Pentru a demonstra ca exista o diferenta de presiune īntre doua faze volumice separate de o faza de interfata curba, sa consideram un element infinit mic din interfata, privita ca suprafata de diviziune (modelul lui Gibbs), de dimensiuni ds₁ si ds₂ (fig. 11.5.).

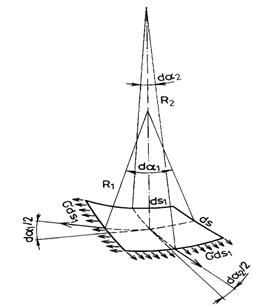
Fig. 11.5. Elementele gometrice ale unei interfete curbe.

Razele principale de curbura sunt R₁ si R₂, iar unghiurile la centru dintre normala la interfata īn centrul de curbura si cele doua raze sunt d /2 si, respectiv, d

Curbura suprafetei, c, se defineste prin relatia:

(11.4.)

Proiectia tensiunii interfaciale, ca forta uniform distribuita pe contur, pe planul tangent īn centrul de curbura este nula. Proiectia pe normala la interfata, dF_n, este urmatoarea:

(11.5.)

Daca se īmparte aceasta forta la aria interfetei (ds₁∙ds₁) se obtine diferenta de presiune dintre fazele volumice despartite de interfata, denumita diferenta capilara de presiune^*). Expresia este urmatoarea:

Unii autori folosesc termenul de presiune capilara īn locul celei de diferenta capilara de presiune. Pentru acuratetea exprimari este preferabil termenul de diferenta capilara de presiune.

(11.6.)

Aceasta se numeste legea lui Laplace.

Cānd interfata este simetrica, avānd forma unei calote sferice, ca īn cazul īn care interfata se afla īntr-un canal cilindric, cele doua raze principale de curbura sunt egale cu raza sferei, R.

Daca se noteaza cu complementul unghiului la centru (denumit si unghi de contact) si cu r, raza cilindrului (fig. 11.6.), expresia legii lui Laplace, este:

(11.7.)

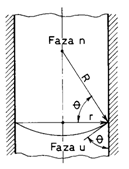
Fig. 11.6. Elementele geometrice ale interfetei īntr-un cilindru.

Din cele doua expresii ale legii lui Laplace, se observa ca diferenta capilara de presiune este cu atāt mai mare cu cāt curbura interfetei este mai mare, adica cu cāt dimensiunea capilarului este mai mica. Cānd dimensiunea spatiului se ma- reste, diferenta capilara de presiune scade devenind, la un moment dat, negli- jabila. Aceasta este limita de la care un spatiu nu mai este considerat capilar.

O aplicatie importanta a diferentei capilare de presiune este ascensiunea si depresiunea capilara (fig. 11.7,a, respectiv b). Pentru simplificare, vom consi-dera interfata dintre un lichid si aer. Diferenta de densitate foarte mare, permite neglijarea, īntr-o prima aproximatie, a densitatii aerului īn raport cu cea a lichidului.

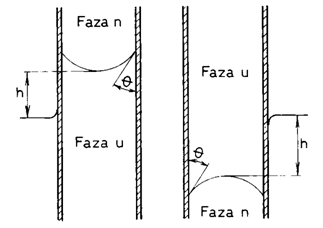
a.   b.

Fig. 11.7. Ascensiunea si depresiunea capilara.

Daca interfata ar avea acelasi nivel īn capilar si īn afara lui, ca īn cazul vaselor comunicante, ar īnsemna ca presiunea lichidului de sub interfata este egala cu presiunea atmosferica. Aceasta ar contrazice legea lui Laplace. Prin ridicarea nivelului interfetei īn capilar, presiunea lichidului de sub interfata scade cu presiunea hidrostatica a coloanei de lichid, ρgh, pāna cānd este egalata diferenta capilara de presiune. Atunci ridicarea interfetei īnceteaza, stabilindu-se echilibrul dintre cele doua presiuni. Daca se renunta la simplificarea acceptata mai sus, aceea a neglijarii densitatii aerului īn locul densitatii, , se introduce diferenta de densitate,

Īnaltimea de ridicare a interfetei, h, este data de relatia (legea lui Jurin):

(11.8.)

Rationamentul este identic si pentru depresiunea capilara. Atingerea echilibrului de presiune presupune marirea presiunii lichidului cu o valoare egala cu diferenta capilara de presiune, ceea ce se īntāmpla daca punctul de masurare a presiunii coboara sub nivelul lichidului din afara capilarului.

O alta modalitate de a explica ascensiunea capilara (ca si depresiunea capilara) este echilibrul dintre forta de interfata si forta de greutate. Referindu-ne la figura 11.7,a., proiectia fortei de interfata pe axul capilarului este data de expresia:

(11.9.)

Greutatea coloanei de lichid, G, este data de expresia:

(11.10.)

Egalānd cele doua expresii, obtinem relatia (11.8.), care se mai poare scrie:

(11.8'.)

Produsul r h = a² se numeste constanta capilara. Denumirea vine de la faptul ca toate marimile din membrul drept al relatiei (11.8'.) sunt constante pentru o pereche de fluide aflate īn capilare din acelasi material.

Relatiile de mai sus, referitoare la echilibrul de forte sau de presiuni contin o aproximatie: nu a fost luata īn considerare greutatea aparenta a fluidului de sub menisc (mai corect forta de plutire a meniscului). La valori mici ale īnaltimii si valori mari ale razei, eroarea poate fi semnificativa. Pentru corectie, se poate folosi relatia lui Rayleigh [90]:

(11.11.)

Diferenta capilara de presiune joaca un rol major īn procesele de exploatare a zacamintelor de hidrocarburi, asa cum se va vedea īn capitolele urmatoare.

Aplicatia 4.

Dintr-un titei aflat la presiunea de 100 bar ies din solutie gaze care formeaza bule cu diametrul d = 2 m. Sa se calculeze presiunea din interiorul bulelor. Se cunoaste tensiunea superficiala a titeiului 40 mN/m.

Raspuns.

Diferenta capilara de presiune la interfeta titei-gaze este data de relatia (11.6.). Curbura sferei este c = 4/d. Rezulta: _cp = 4∙40∙10^-3/2∙10^-6 = 8∙10⁴ N/m² = 0,8 bar. Cum diferenta de presiune capilara se manifesta spre concavitata interfetei, presiunea din bule va fi: p = 100,8 bar. Prin faptul ca presiunea din interiorul bulelor de gaz este mai mare decāt cea din titei, iesirea gazelor din solutie īn pori se produce cu o oarecare īntārziere fata de datele experimentale din instalatiile pVT.

Aplicatia 5.

Pentru determinarea tensiunii interfaciale a benzenului prin metoda ascensiunii capilare īntr-un canal cilindric cu raza r=0,55 mm s-a obtinut o īnaltime de ridicare a meniscului de 12,01 mm (masurata pāna la tangenta orizontala la menisc). Cunoscānd densitatea benzenului la 20⁰C, _b 878,5 kg/m³ si cea a aerului, _aer 1,205 kg/m³ si considerānd unghiul de contact 0, sa se calculeze tensiunea interfaciala.

Raspuns.

Se foloseste relatia (11.8'.) pentru constanta capilara. Rezulta: a²=5,6055∙10^-6m² si =28,424 mN/m. Corectia de īnaltime se face cu relatia (11.11.). Constanta capilara corectata va fi: a²=6,7045 m² iar tensiunea superficiala 28,854 mN/m. Eroare este acceptabila:

Aplicatia 6.

Sa se determine diferenta capilara de presiune la suprafata unui inel de apa dispus īn jurul punctului de contact a doua sfere cu raza R = 0,1 mm, īn ipoteza ca interfata apa-aer este tangenta la suprafata solida.

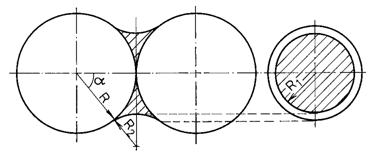
Raspuns.

Īn figura [98] este reprezentata pozitia inelului fata de sfere. Se observa ca cele doua raze de curbura ale interfetei au sensuri diferite (centrele de curbura se afla de o parte si de cealalta a interfetei, fata de cazul din figura 11.5. Astfel, R₁ va fi pozitiv iar R₂ va fi negativ). Cele doua raze de curbura depind de pozitia, respectiv de volumul inelului. Daca notam cu unghiul dintre linia centrelor si raza la punctul de contact dintre inel si sfera, se poate:

.

Diferenta capilara de presiune va fi:

.

Considerānd 72 mN/m, pentru 300 si = 100 obtinem urmatoarele valori:

_cp = 2,94 mN/m si, respectiv, _cp = 42,26 mN/m, adica presiuni īn interiorul inelului de apa de 300 mmcolH₂O, respectiv, 4,32 mcolH₂O.

De remarcat cresterea substantiala a diferentei capilere de presiune la micsorarea volumului inelului de apa.

Aplicatia 7.

Tensiunea superficiala a unui lichid este masurata prin ascensiune capilara diferentiala (ascensiunea īn doua tuburi cilindrice paralele de raze diferite). Se masoara diferenta de nivel dintre cele doua meniscuri, h.

Se cunosc: r₁ = 1 cm; r₂ = 1 mm; _L = 800 kg/m³ (la 20⁰C).

Se cere sa se calculeze:

1. Tensiunea superficiala a lichidului;

2. Eroarea introdusa de neglijarea densitatii aerului īn raport cu cea a lichidului;
3. Eroarea introdusa prin neglijarea greutatii meniscurilor.

Raspuns.

Solutia 1. Se calculeaza constanta capilara: a² = r h = r₁ h₁ = r₂ h₂.

Din ultima egalitate rezulta: r₁/r₂ = h₁/h₂ = (h₂+ Δh)/h.

Rezulta: h₂ = Δh/(r₁/r₂ - 1); h_i = h₂ r₂/r₁.

Din aplicatia numerica rezulta: h₁ = 18,889 mm, h₂ = 1,889 mm si a² = 18,889 mm².

Egalānd diferenta capilara de presiune cu presiunea hidrostatica, rezulta:

σ = a² Δ ρ g/2.

Cunoscānd ρ_aer = la 1,205 kg/m³ 20⁰C, rezulta: σ = 74,12 mN/m.

Solutia 2. Se considera un capilar cu raza echivalenta, r (īn care īnaltimea de ridicare este h iar constanta capilara este a² = r h ): r = 1/r₁ - 1/r₂.

Īnlocuind valorile numerice, obtinem: r = 1,111 mm si a² = 18,889 mm², adica aceeasi va-loare ca la solutia precedenta. Evident, tensiunea superficiala calculata va fi aceeasi.

b) Neglijarea densitatii aerului īnsemneaza īnlocuirea lui cu īn relatia de calcul a tensiunii interfaciale. Prin aceasta neglijare, rezulta 74 mN/m.

Eroarea relativa este de 0,162%.

c) Corectia pentru greutatea meniscurilor consta īn recalcularea īnaltimilor de ascensiune īn fiecare capilar, īn sensul adaugarii la īnaltimea conventionala (masurata pāna la partea de jos a meniscului) a unei unor diferente corespunzatoare volumelor meniscurilor. Corectia se face cu relatia lui Rayleigh:

a² = r(h + r/3 + 0,1288 r²/h + 0,1312 r³/h² + .)

Pentru capilarul cu r = 1 mm, rezulta a₁² = 19,22 mm².

Pentru capilarul cu r = 1 cm, avānd īn vedere apropierea valorilor r si h, relatia lui Rayleigh nu mai este valabila. Īn acest caz, constanta capilara se calculeaza cu relatia: a² = b h, unde b este o marime echivalenta cu raza capilarului si poate fi luata sub forma raportului r/b dintr-unul din tabelele de mai jos.

r/a

Valorile raportului r/b īn functie de raportul r/a, pentru r/a >

Calculul este iterativ, cu urmatorii pasi:

Rezulta: h₂ = 3,734 mm; Δh = 15,486 mm; a² = 17205 mm² si σ = 67,42 mN/m.

Prin neglijarea greutatii meniscurilor eroarea este de 9,93%, inacceptabila la o determinare experimentala. De aceea se impune corectia prezentata mai sus.

Aplicatia 8.

Īn figura sunt reprezentate sase capilare de sticla cu aceeasi raza. Doua dintre ele au zone cu sectiune marita, iar unul are o zona īn care sticla este īnlocuita cu parafina. Īn capilarul "a" e ste aratata pozitia de echilibru a interfetei, rezultata din eglitatea fortei de interfata cu cea de plutire. Sa se explice pozitia interfetei īn capilarul "e" si existenta a doua interfete īn celelalte capilare.

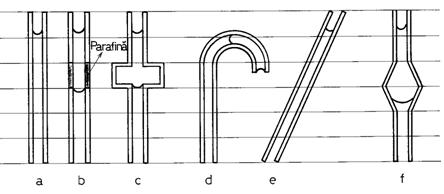
Indicatie: Se va avea īn vedere "istoria" ascensiunii capilare, īn sensul ca initial acestea sunt pline cu aer si sunt aduse īn aceasta pozitie de sus īn jos sau, din contra, sunt pline cu apa si se ridica pāna la pozitia din figura.

Īntrebari si probleme

Prin ce se deosebeste tensiunea interfaciala de energia de suprafata?

Tensiunea interfaciala este un vector sau un scalar?

Care este diferenta īntre tensiunea superficiala si tensiunea interfaciala?

Cum influenteaza contrastul de compozitie tensiunea interfaciala?

Care este mecanismul de actiune al tensidelor asupra tensiunii interfaciale?

Cum actioneaza solutia de hidroxid de sodiu asupra tensiunii interfaciale apa-titei si care este conditia unui efect maxim?

Definiti conceptul de faza de interfata.

Care este ordinul de marime al tensiunii interfaciale apa-titei?

Cum se defineste diferenta capilara de presiune?

De ce se recomanda "diferenta capilara de presiune" si nu "presiune capilara"?

Care este valoarea diferentei capilare de presiune pentru o interfata plana?

Care este diferenta īntre legea lui Laplace si cea a lui Jurin?

Presiunea mai mare īn partea concava sau īn cea convexa a unei interfete curbe?

Daca interfata este sub forma de sa (cānd sunt doua centre de curbura, de o parte si cealalta a interfetei) unde este presiunea mai mare?

Cum se defineste constanta capilara?

De ce uneori interfata urca īntr-un capilar, iar alteori coboara.

Sa se calculeze presiunea din interiorul unei picaturi de titei cu raza de 0,01 mm aflata īntr-un vas cu apa la adāncimea de 10 cm. De da tensiunea interfaciala apa-titei, .

Se considera un capilar sub forma de cu raza de 0,1 mm care se introduce īntr-un vas cu titei () cu ambele brate deodata. Sa se calculeze īnaltimea de ascensiune capilara.

Indicatie: se va tine seama de contrapresiunea aerului captiv din capilar.

Se considera doua tuburi capilare cilindrice introduse īntr-un vas cu apa. Īntr-unul din tuburi se adauga pe la partea superioara o cantitate infima de substanta tensioactiva care va duce la scaderea la jumatate a tensiunii interfaciale. Sa se precizeze īn ce sens si cu cāt se va deplasa interfata din acest capilar īn comparatie cu celalalt.