RĪGAS TEHNISKĀ UNIVERSITĀTE

ELEKTRONIKAS UN TELEKOMUNIKĀCIJU FAKULTĀTE

ELEKTRONIKAS PAMATU KATEDRA

Laboratorijas darbs Nr. 2.b)

Iepazīsanās ar periodisku signālu izvērsi trigonometrisku funkciju Furjē rindā.

Sergejs Tjukovs

II kurss, REBJO1

031REB224

Rīga - 2005.

Mājas darbs.

1. variants.

Signāls:

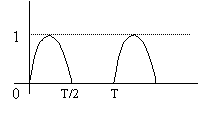
To var aprakstīt kā: s(t)=sin(2*pi*t/T), kad 0 t T/2

s(t)=0, kad T/2 t T

Signāla izvērse Furjē rindā.

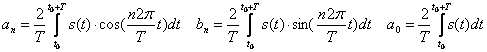(1)

;

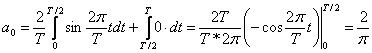
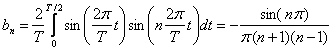Iegūtie rezūltāti tika pārbaudīti, izmantojot Matlab programmu:

syms t T n;

a0=(int(sin(2*pi*t/T),t,0,T/2))/T;% seit a0=a0/2

an=2*(int(sin(2*pi*t/T)*cos(2*n*pi*t/T),t,0,T/2))/T;

bn=2*(int(sin(2*pi*t/T)*sin(2*n*pi*t/T),t,0,T/2))/T;

2

a₀=----

pi

cos(n pi) + 1

a_n=- ----- ----- ---------

pi (1 + n) (-1 + n)

sin(n pi)

b_n=- ----- ----- ---------

pi (1 + n) (-1 + n)

Apskatot a_n un b_n, var secināt, ka pie n=1 tos nevar aprēķināt, tāpēc a₁ un b₁ atrasanai izmantosu formulas (1) pieņemot ka n=1:

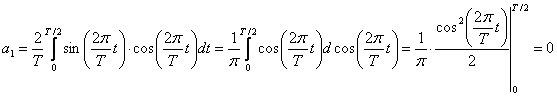
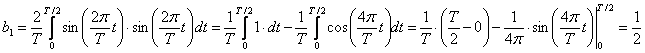
Furjē rinda:

System View blokshēma kas nodrosina dotā signāla realizāciju:

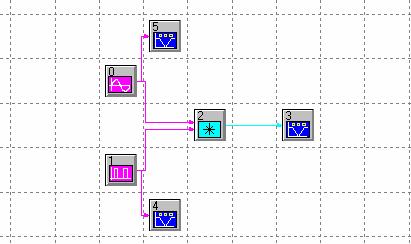
Avotu parametri:

0 avots: Amplitude(V)=1, Frequency(Hz)=1.

1 avots: Amplitude(V)=1, Frequency(Hz)=1, Bias(V)=0, Pulse Width(sec)=500e-3.

System View blokshēma kas nodrosina atrasto harmoniku summas realizāciju:

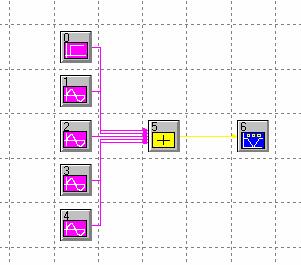
Avotu parametri:

0 avots: Amplitude(V)=318,3e-3; Start Time(sec)=0; Bias(V)=0.

1 avots: Amplitude(V)=500e-3; Frequency(Hz)=1; Phase(deg)=0.

1 avots: Amplitude(V)=-212,2e-3; Frequency(Hz)=2; Phase(deg)=90.

1 avots: Amplitude(V)=-42,4e-3; Frequency(Hz)=4; Phase(deg)=90.

1 avots: Amplitude(V)=-18,2e-3; Frequency(Hz)=6; Phase(deg)=90.

System Time parametri: Sample Rate=64Hz; No. of Samples=256.

Darbs laboratorijā.

Signāls.

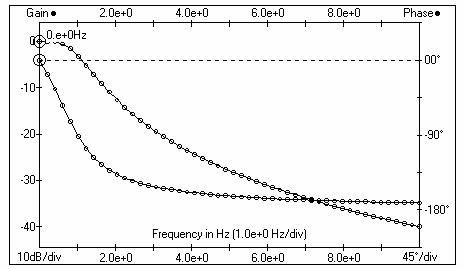
Filtra frekvenču raksturlīkne( f=1Hz)

Filtra ieejā un izejā

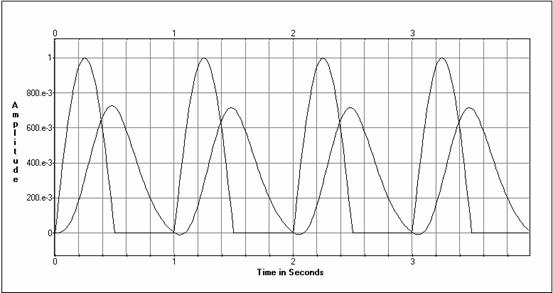
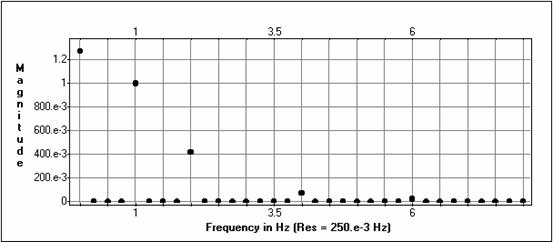
Ieejas amplitūdu spektri

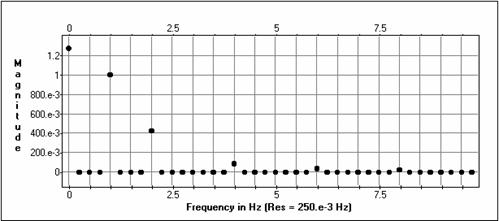
Izejas amplitūdu spektri

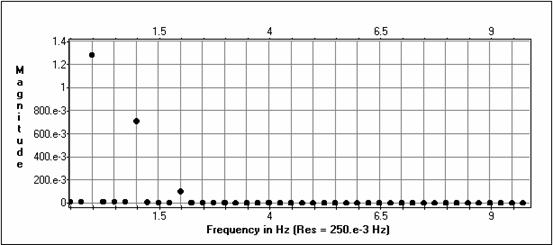
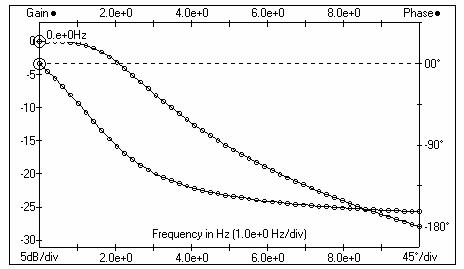
Filtra frekvenču raksturlīkne( f=2Hz)

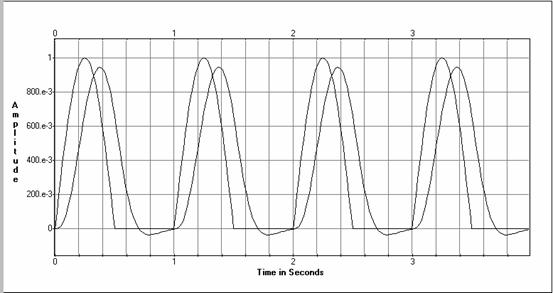
Filtra ieejā un izejā

Izejas amplitūdu spektri

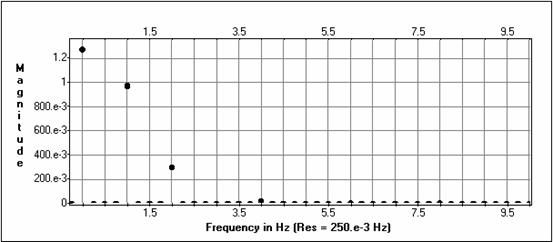
Filtra frekvenču raksturlīkne( f=5Hz)

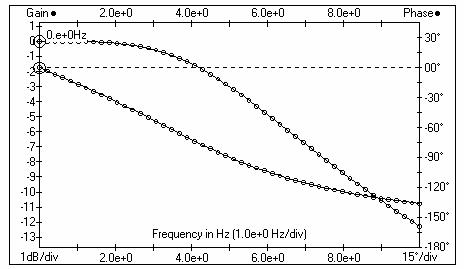
Filtra ieejā un izejā

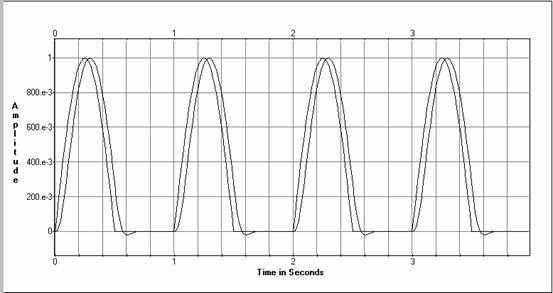
Izejas amplitūdu spektri

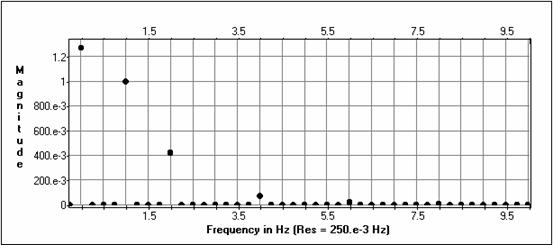
Harmoniku summas realizācija.

Filtra nogriesanas frekvence ir 1Hz.

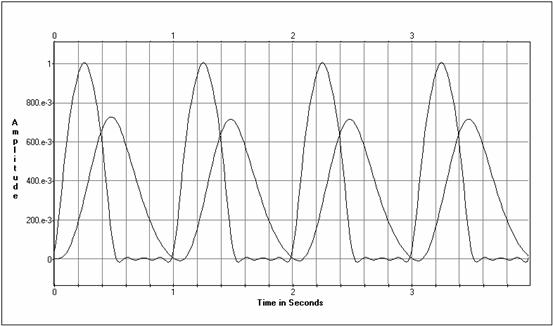
Ieejas un izejas laika diagrammas

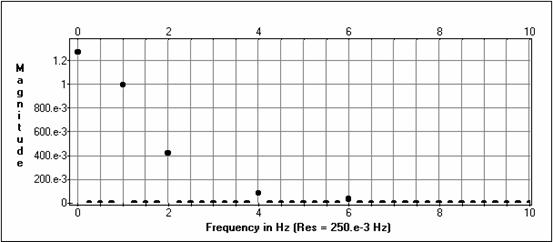
Ieejas amplitūdu spektri

Izejas amplitūdu spektri

Filtra nogriesanas frekvence ir 2Hz.

Ieejas un izejas laika diagrammas

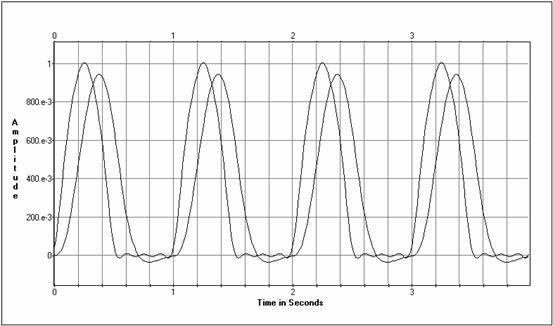
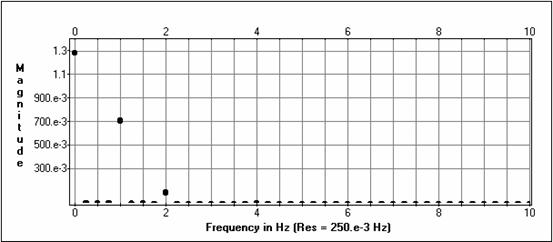
Izejas amplitūdu spektri

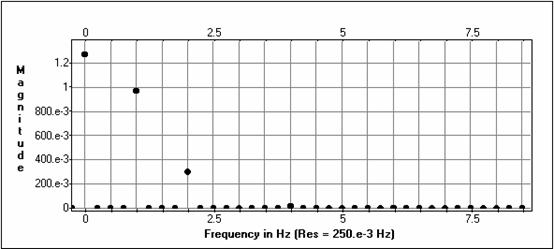
Filtra nogriesanas frekvence ir 5Hz.

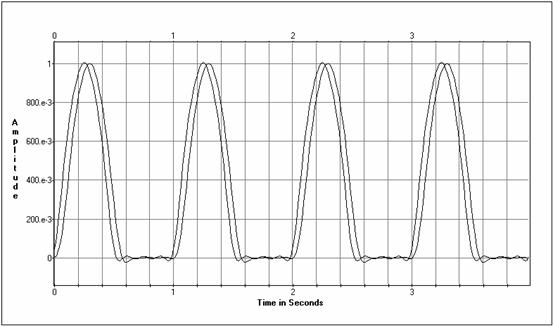
Ieejas un izejas laika diagrammas

Izejas amplitūdu spektri

Secinājumi.

Izpildot so laboratorijas darbu, es iemācījos izvērst doto periodisko signālu trigonometrisku funkciju Furjē rindā. Tika noteikta signāla līdzkomponente un pirmās četras harmonikas. Ar System View izveidoju blokshēmas ar kuru palīdzību pārliecinājos, ka dotais signāls un harmoniku summa gandrīz sakrīt. So starpību var samazināt paņemot ļoti lielu harmoniku skaitu.

Ar System View tika iegūti dazādi ieejas un izejas signālu amplitūdas spektri. Analizējot tos, izrādījas ka System View rēķinā signāla spektrālo blīvumu: 0.5*Ċ_nT (mūsu gadījumā T=1s), bet tā kā tika ņemti signāla četri periodi tad jāreizina ar 4T, sādā gadījumā mēs iegūstam sakarību starp aprēķinātas Furjē rindas harmoniku amplitūdām un to ko rāda System View: 0.5*Ċ_n4T.

Laboratorijas darba laikā es arī pārliecinājos, ka Furjē rindu ir ļoti ērti izmantot, analizējot periodisku signālu pārvadi lineārās sistēmās. Būtiski ir tas, ka lineāras sistēmas (RLC ķēdes) periodisku signālu "redz" kā sastāvosu no harmonikām. Sī iemesla dēļ, zinot signāla amplitūdu un fāzu spektru diagrammas, kā arī lineāras sistēmas amplitūdas frekvenču raksturlīknes, ir iespējams noteikt izejas signālu. Laboratorijas darba laikā, mēs pētījām dotā signāla, kā arī harmoniku summas pārvadi zemo frekvenču Batervorta filtrā ar diviem poliem, mainot tā parametrus. Seit es sīkāk apskatīsu situāciju, kad filtra nogriesanas frekvence ir 1Hz:

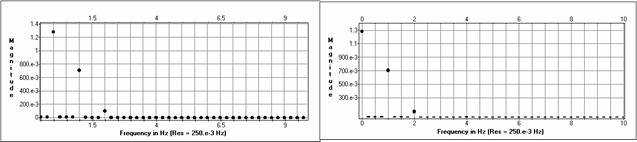
Harmoniku summas spektrs

Filtra ieejā

Līdzīga situācija ir arī tad, kad filtra nogriesanas frekvences ir 2Hz un 5Hz. Tikai tad pieaug to harmoniku skaits, kuru amplitūdas netiek vājinātas.

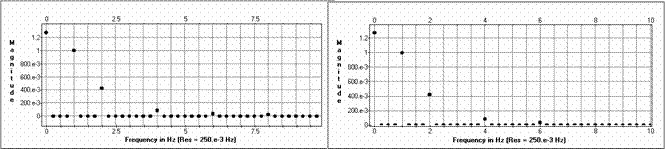
No filtra amplitūdas frekvenču raksturlīknes ir redzams, ka signāli ar frekvenci lielāku par 1Hz tiek būtiski vājināti, tāpēc harmoniku ar frekvenci lielāku par 2.5 Hz amplitūdas ir tik niecīgas, ka tās var neņemt vērā. Tādejādi, neskatoties uz to, ka filtra ieejā dotais signāls un harmoniku summa atsķirās, izejā tie būs praktiski vienādi, jo to spektri arī būs gandrīz identiski. Izejas spektri

Dota signāla spektrs

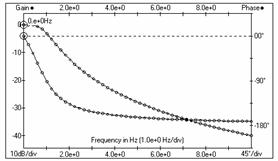
Filtra amplitūdas frekfenču raksturlīkne