Одноетапні задачі стохастичного пр&# 151j92b 1086;грамування

Розглянемо лінійну одноетапну задачу стохастичного пр&# 151j92b 1086;грамування в такій постановці: визначити план Х, для якого

— нормально розподілена випадкова величина з математичним сподіванням і дисперсією і — нормально розподілені випадкові величини з математичними сподіваннями відповідно та і дисперсіями

та вектор є нормально розподіленими випадковими величинами, то їх різниці також є випадковими величинами з нормальним розподілом, математичним сподіванням і дисперсією

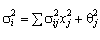
еквівалентні нері нормально розподілена випадкова величина, використаємо функцію нормального закону розподілу, внаслідок чого наведену нерівність можна записати так:

і

Таку задачу можна розв’язати одним з відомих методів розв’язування задач нелінійного пр&# 151j92b 1086;грамування, наприклад, методом множників Лагранжа.

Розглянемо одноетапну задачу стохастичного пр&# 151j92b 1086;грамування, що задана Р-моделлю. Отже, маємо задачу виду:

У даній задачі необхідно мінімізувати величину k, що обмежує витрати на виготовлення продукції

— нормально розподілена з математичним сподіванням і кореляційною мат­рицею буде випадковою величиною, що також нормально розподілена з математичним сподіванням та дисперсією

величина є угнутою функцією за змінними . Отже, за зроблених допущень задачі стохастичного пр&# 151j92b 1086;грамування

Остання задача являє собою задачу опуклого пр&# 151j92b 1086;грамування. Для її розв’язування можна застосувати теорему Куна—Таккера, або один з інших методів розв’язування задач нелінійного пр&# 151j92b 1086;грамування.

для кожної і-ої поживної речовини

— відповідно обсяги ячменю, кукурудзи і гороху, які необхідно закупити.

— відповідно потреби кормових одиниць, перетравного пр&# 151j92b 1086;теїну, лізину та кальцію (випадкові, рівномірно розподілені величини).

— відповідно значення випадкових величин, що задовольняють умови:

і

і

З теорії ймовірностей відомо, що:

Звідси: або тому