TEORIA DECIZIEI SI APLICATII DE MARKETING

TEORIA DECIZIEI SI APLICATII DE MARKETING

DECIZII IN CONDIŢII DE INCERTITUDINE

In comparatie cu deciziile probabiliste, deciziile īn conditii de incertitudine sunt inferior structurate, īn sensul ca lipsesc informatiile necesare stabilirii probabilitatilor producerii starilor naturii īn contextul carora au loc procesele economice.

Pentru a rezolva situatiile de incertitudine, trebuie structurata o matrice A, īn care elemente a_ij reprezinta platile (profit sau costuri) aferente situatiei date.

Literatura de specialitate prezinta cinci criterii specifice de decizie, care pot fi aplicate īn conditii de incertitudine.

Criteriul pesimist sau regula lui Wald conform caruia se alege ca optima, varianta care asigura plata minima cea mai mare (maximin) sau atunci cānd exista plati negative - paguba cea mai mica, folosind relatia (7.10):

īn care a_ij reprezinta platile jocului, īn ipoteza ca jucatorul rational (managerul, proiectantul, antreprenorul) aplica varianta V_j (iar natura se manifesta cu starea S_j)

V' - varianta optima.

Concluzie:

Se observa ca acest criteriu foloseste numai o singura valoare de la fiecare varianta, o mare cantitate de informatii ramānānd neutilizata.

Atunci cānd platile din matricea jocului A reprezinta eforturi ca investitii, cheltuieli de productie, consumuri specifice, īn locul relatiei (7.10) se va folosi o relatie reciproca, adica (7.11):

Criteriul optimist este opus celui perimist. Se prefera varianta care conduce la plata cea mai mare din matricea A, indiferent de urmarile negative ce ar putea sa aiba loc. Relatia cu ajutorul careia se identifica varianta optima īn acest caz preconizeaza specificarea valorii maxime pe fiecare linie a matricii A, dupa care se va opta pentru linia care asigura conditia (7.12).

Acest criteriu asigura alegerea variantei cu cel mai mare potential de cāstig, dar prezinta - de obicei - si riscuri considerabile.

Criteriul optimistului ponderat sau regula lui Hurwicz balanseaza consecintele celor doua criterii anterioare,. Astfel, pentru fiecare varianta de actiune V_I se calculeaza o valoare ponderata, folosind relatia (7.13).

unde α reprezinta coeficientul de optimism al decidentului, marime normata īn limitele α ε [0, 1]. Relatia pe baza careia se ia decizia īn acest caz este (7.14).

Se observa ca varianta optima rezultata īn cazul criteriului 3 are cel mai mic risc.

Criteriul regretelor minimax sau regula lui Savage implica stabilirea īn prealabil a unei matrici a regretelor R

construita cu elemente r_ij definite drept pierderi de oportunitate care se produc īn caz ca nu este selactata varianta optima, la producerea fiecarei stari S_j a naturii. Formula de calcul a regretelor este (7.15).

L. Savage a argumentat ca īn cazul folosirii acestui criteriu, decidentul tinde sa adopte varianta V_i care va minimiza cel mai mare regret anticipat, conform relatiei (7.16).

Criteriul lui Laplace sau criteriul echiprobabilitatilor se bazeaza pe un postulat a lui Bernoulli, care afirma ca, daca este data o multime de evenimente si nu se poate spune despre nici unul ca are o probabilitate mai mare de a se manifesta decāt celelalte, atunci toate evenimentele sunt echiprobabile. In consecinta, criteriul lui Laplace determina pentru fiecare varianta speranta matematica a platilor aferente E_i calculate cu relatiei (7.17).

urmānd a se considera ca optima, acea varianta care īndeplineste conditia (7.18).

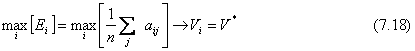
Pentru fiecare criteriu, asteriscul marcheaz[ solutia optima

2.2. JOCURI STRATEGICE

Domeniu cel mai propice pentru folosirea modelelor de joc īn vederea adoptarii deciziilor este cel al relatiilor competitionale dintre indivizi independenti, compartimente sau grupuri de indivizi, organizatii sau grupuri de organizatii

O mare parte din jocurile īntre parteneri rationali si anume cele analitice, sunt asociate unor probleme relativ bine structurate cu caracter repetitiv (exemplu: concurenta dintre ofertantii de produse similare pe o piata libera, sau competitile dintre compartimentele unei firme pentru adjudecarea unui cuantum cāt mai mare din fondul de investitii alocat).

JOCURI STRATEGICE CU SUMĂ NULĂ

Jocul strategic de doua persoane cu suma zero poarta aceasta denumire deoarece cāstigul unuia din jucatori este egal cu pierderea celuilalt jucator, astfel ca din suma acestora se obtine valoarea zero.

Īn regulile unui joc intervin urmatoarele elemente:

cel putin doi jucatori, maximizantul J₁ si minimizantul J₂,

strategiile de joc a fiecarui jucator sunt cunoscute (S_I si s_j),

matricea de plati (matricea consecintelor jocului) A = ║ a_ij║.

Jocurile de doua persoane cu suma nula definite de elementele enumerate se considera jocuri cu informatie completa. Fiecare jucator are strategia sa, unul maximizeaza (aplica criteriul MAXIMIN)

celalalt minimizeaza (aplica criteriul MINIMAX)

iar jocul se echilibreaza īntr-un punct, care indica valoarea jocului. Din rezolvarea jocurilor strategice astfel definite se cunosc doua tipuri de strategii:: (a) strategii pure, (b) strategii mixte.

Strategiile pure apar atunci cānd dupa ce jucatorii īsi aplica propriile criterii de decizie, se verifica relatia:

rezultānd pentru fiecare jucator o singura strategie optima (cu conditia v = 0). Valoarea care satisface conditia (7.19) este valoarea jocului (v), pentru care exista doua situatii:

daca v > 0 cāstiga maximizantul,

daca v < 0 cāstiga minimizantul.

In cazul strategiilor mixte (strategii combinate) nu se īndeplineste conditia (7.19). Aceste strategii implica un proces de urmarire a adversarului si cumulare de la o varianta la alta, astfel īncercānd atingerea propriului obiectiv. Rezolvarea unei asemenea probleme solicita determinarea proportiilor fiecarui jucator sa contracareze cu strategia sa, astfel ca sa rezulte o valoare optima.

JOCURI STRATEGICE CU SUMĂ CONSTANTĂ sI COOPERĂRI

Īn aceste jocuri se ofera o "miza" de joc care este adjudecata de catre parteneri proportional cu calitatea strategiilor utilizate. Aceste jocuri folosesc matrici de plati diferite, astfel maximizantul foloseste matricea A = ║ a_ij║., iar minimizantul are matricea B = ║ b_ij║. De aceea, aceste jocuri se mai numesc si "bimatriciale", si pot avea unul sau doua puncte de echilibru.

Partenerii trebuie sa stabileasca seturi optime de strategii, prin īntelegere (exemple: pot sa īsi exercite independent politicile lor de promovare, preturi, conditii de piata, dar pot sa coopereze īn ceea ce priveste serviciile post-comerciale acordate clientilor). Aceste conventii apar datorita economiilor ce se pot obtine pe baza efectelor de scara a volumului de activitati ce se pot realiza īn comun. Cooperarile de acest tip maresc cāstigurile firmelor, chiar daca īn restul politicilor lor se comporta concurential.

2.3. DECIZII IN CONDIŢII DE RISC

Riscul este ceea ce "se pune la bataie", decidentul angaajāndu-se pe o cale īn conditiile īn care s-ar putea sa fie altul decāt cel scontat. Oamenii au capacitati de risc diferite īn functie de caracteristicile lor biologice si de puterea lor economica.

Omul nu poate elimina complet riscul īn cazul cānd au loc fenomene aleatoare. Īnsa, sta īn puterea lui sa reduca riscul, pāna la un nivel minim care sa-I faca acceptabil. Pentru aceasta se procedeaza la o analiza probabilistica de evaluare si de selectie decizionala.

Metodele cantitative cele mai des īntrebuintate īn acest sens sunt speranta matematica a rezultatelor si arborii de decizie.

2.4. APLICAŢII

Enunt:

Īn vederea lansarii pe piata a unui nou calculator (PC), o firma de specialitate trebuie sa opteze pentru cea mai buna varianta de asimilare din trei posibilitati (V₁, V₂, V₃), caracterizate sumar, īn conditii de incertitudine, conform datelor din tabelul 7.2.

Deoarece o serie de date importante legate de productie, testare, comercializare si exploatarea produsului la beneficiari nu sunt disponibile, se recomanda alegerea solutiei optime pe baza de utilitati.

Tabelul 7.2 -Informatii pentru alegerea variantei de asimilar,

pentru un computer (PC)

Rezolvare:

Pentru a aplica relatia (7.9), trebuie construita matricea A. Ponderile _j se determina cu algoritmul STEM - relatia (2.2). Astfel, matricea A este de forma:

C₁ C₂ C₃

Coeficientii a_ij au fost stabiliti astfel:

1, daca C_j este la fel de important ca C_i

a_ij= 2. Daca C_j este mai important ca C_i

0, īn rest

Ponderile _j au urmatoarele valori:

Utilitatile la criteriul C₁:

u(V₁)₁=1, u(V₂)₁=0, iar pentru u(V₃)₁=3/5, pentru ca se aplica relatia (7.5).

Utilitatile pentru C₂ sunt:

u(V₁)₂=0, u(V₂)₂=1, iar pentru u(V₃)₂=3/5

Utilitatile pentru C₃ au valorile:

u(V₁)₃=1, u(V₂)₃=0, iar pentru u(V₃)₃=2/5

Utilitatile globale calculate au urmatoarele valori:

U₁= (3/9).1+(8/9).0+(1/9).1= 4/9

U₂= (3/9).0+(8/9).1+(1/9).(2/5)= 3/5

U₃= (3/9).1+(8/9).(3/5)+(1/9).0= 8/15

Pentru a le putea compara, aceste utilitati se aduc la acelasi numitor:

U₁=20/45, U₂= 27/45, U₃=24/45

CONCLUZIE: V₂ P V₃ P V₁.

Enunt:

Un investitor doreste sa-si valorifice banii disponibili. Pentru acest scop, solicita consultanta de la o organizatie specializata īn consultanta financiara si-i solicita un studiu de oportunitate. Īn tabelul 7.3 prezentam matricea de plati, ca rezultat al investigatiilor facute pentru patru variante de solutionare a problemei. Platile reprezinta ratele anuale de recuperare a capitalului pentru variantele respective.

Consultantul nu a reusit sa stabileasca probabilitatile starilor naturii. Capitalul este de 100.000 UM. Dar firma de consultanta se obliga sa indice varianta optima, garantānd solutia recomandata clientului.

Tabelul 7.3 - Ratele recuperarii capitalului,

pe variantele de rezolvare a unei probleme de investitie

Rezolvare:

Conform criteriilor de selectie, se obtin solutiile urmatoare:

Crirteriul pesimist conduce la:

max [-2, -10, -6, -4] = -2 V₁ = V^*

Criteriul pesimist foloseste cāte o singura valoare de la fiecare varianta, astfel ca 75% din cantitatea de informatii ramān nevalorificate - pentru problema studiata.

Criteriul optimist ofera solutia:

max [15, 20, 12, 10] = 20 V₂ = V^*

Criteriul optimistului ponderat, decizia este:

max = max [ 6,5; 5; 3; 3] = 6,5 V₁ = V^*

Criteriul regretelor conduce la solutia:

max
; 15; 21; 10] = 10 V₄ = V^*

Criteriul lui Laplace

max [6; 3,5; 1,5; 6,25] = 6,25 V₄ = V^*

Rezultatele aplicarii celor cinci criterii sunt concentrate īb tabelul 7.4.

Tabelul 7.4 - Solutiile problemei de decizie īn conditii de incertitudine,

pentru problema studiata

CONCLUZIE: Situatiile ambigue pot rezulta prin aplicarea īn procesul xclusive a mai multor criterii. De aceea este necesar sa se introduca xclus suplimentare pentru decizie.

Enunt:

Sa se stabileasca valoarea jocului (punctul de echilibru) īntre doi jucatori, J₁ si J₂ - doua firme producatoare de autovehicule (Dacia si Rodae) - pentru care matricea platilor este cea prezentata īn tabelul 7.5.

Tabelul 7.5 - Matricea platilor pentru jocul de marketing studiat

Rezolvare:

Aplicānd relatia (7.19) obtinem:

CONCLUZIE: Valoarea jocului este v = -1, deci cāstiga jucatorul minizant J₂, jocul fiind cu strategii pure. Jucatorul J₁ va trebui sa aplice strategia S₂, iar minimizantul J₂ va raspunde cu strategis s₂.