CAPITOLUL I. CARACTERISTICI PSIHO-PEDAGOGICE ALE COPIILOR DE VÂRSTĂ sCOLARĂ MICĂ , CU IMPLICAŢII ÎN ÎNVĂŢAREA MATEMATICII.......... ..... ...... .......... ..... ...... .......... ..... ...... ...8

CAPITOLUL II NOŢIUNI FUNDAMENTALE ÎN ARITMETICĂ .............54

CAPITOLUL III PREDAREA-ÎNVĂŢAREA OPERAŢIILOR ARITMETICE ÎN ÎNVĂŢĂMÂNTUL PRIMAR -APLICAŢII PRACTICE.......... ..... ...... 71

CAPITOLUL IV CERCETAREA PEDAGOGICĂ.......... ..... ...... .......126

CONCLUZII.......... ..... ...... .......... ..... ...... .......... ..... ...... .....154

BIBLIOGRAFIE.......... ..... ...... .......... ..... ...... .............................157

PROIECT DIDACTIC .......... ..... ...... .......... ..... ...... ....................159

FIsA DE LUCRU.......... ..... ...... .......... ..... ...... ............................163

INTRODUCERE

În contextul actualei reforme curriculare a învatamântului românesc , este firesc ca în centrul preocuparilor actuale ale scolii românesti sa se situeze cultivarea accentuata a gândirii logice a micilor scolari . si cum am putea mai bine rezolva problema decât prin evidentierea relatiilor matematice prin fundamentarea stiintifica a conceptelor , prin introducerea progresiva a limbajului matematic modern. De aceea se impune ca scoala sa ofere elevului mijloacele necesare progresului sau continuu în cunoastere si adaptare . Acest progres trebuie sa se axeze pe însusirea capacitatilor esentiale , pe cultivarea unei gândiri suple , dialectice , sa-i asigure însusirea de sisteme logice , de metode si instrumente de învatare prin activitate proprie. Obiectivele învatamântului matematic , în etapa actuala , deriva din sarcinile generale ale scolii ca subsisteme social unic , precum si din locul matematicii ca disciplina tehnico-stiintifica . Însa , fiecare lectie în parte , considerata o unealta din ansamblul întregului sistem de cunostinte matematice prevazute de programa , necesita o evaluare continua a randamentului scolar , privita îndeosebi sub aspectul nivelului real de cunostinte si deprinderi operationele ale elevului .

Preocuparea pentru constituirea treptat[ a unui câmp motivational adecvat oricarei forme de munca pe care o desfasoara elevul constituie o cerinta pedagogica a organizarii muncii în scoala . Orice cercetare pedagogica este întreprinsa pentru dezvoltarea si perfectionarea continua a procesului de învatamânt , ea poate sa urmareasca generalizarea experientei pozitive sau crearea unei experiente noi . Cercetarea de creare a experientei noi corespunde mai mult cu tendintele actuale de dezvoltarea stiintei, cu cresterea în general a gradului de participare constienta a omului la progresele în toate domeniile . Matematica este disciplina al carui studiu contribuie în mod esential la formarea gândirii logice , a unei judecati riguroase si a ordinii în viata si în munca .

Capacitatea omului de a se adapta este foarte mare si greutatea pe care o întâmpina uneori este o greutate de moment caracteristica fiecarei persoane în parte.

Învatarea matematicii exerseaza gândirea , antreneaza capacitatea de organizare logica a ideilor , întareste atentia si mareste puterea de concentrare în intensitate si durata , antreneaza memoria logica , dezvolta un ascutit simt critic constructiv si gustul pentru obiectivitate si precizie .

Importanta si actualitatea temei

Modernizarea învatamântului matematic înseamna în primul rând includerea în continutul acestei discipline a cuceririlor acumulate si tratarea ei ca stiinta a structurilor precum si asimilarea lor într-o maniera moderna .

Învatamântul din clasele I-IV are bogate valente formative . Acum se pun bazele sistemului de notiuni care se dezvolta si se aprofundeaza pe tot parcursul scolaritatii , acum se formeaza deprinderile elementare de munca intelectuala.

Înoirea învatamântului matematic înseamna aducerea la zi a continutului acestui

învatamânt , a metodologiei lui , a relatiilor si structurilor , în jos pâna la gradinita . La clasele I-IV când se formeaza notiunea de operatie nu se face un studiu teoretic al problemei. Învatatorul trebuie sa cunoasca cu claritate definitia ficarei operatii cu numere naturale si proprietatile acestora . Aceste cunostinte vor facilita formarea notiunii de operatie adunare-scadere , înmultire-împartire , la nivelul de întelegere al elevulilor .Astfel învatatorul va urmari constientizarea de catre elevi a procesului de cunoastere a semnificatie operasiilor , cât si a principiilor ce stau la baza aplicarii lor în calcul .

Pe treapta învatamântul primar , respectiv clasele I-IV , copiii trebuie sa vina în contact cu numeroase situatii problematice , care sa-i stimuleze la o gândire matematica .

Primul contact al copilului cu matematica consta în actiunea de a numara obiactele din jurul sau . Intrat în scoala , notiunea fundamentala ce se însusesete este notiunea de numar natural si operatiile cu acestea. Aceste notiuni vor sta la baza însusirii notiunilor matematice în ciclul gimnazial . Putem afirma fara a gresi ca cerintele majore ale învatarii matematicii la ciclul primar o reprezinta si asigurarea continuitatii cu instruirea din învatamântul gimnazial .

Motivarea alegerii temei.

Pornind de la ideea ca matematica a devenit în zilele noastre un instrument esential de lucru pentru totalitatea stiintelor si domeniilor tehnice , este firesc ca în centru preocuparilor actuale ale scolii românesti sa se situeze cultivare accentuata a gândirii micilor scolari , prin evidenta relatiilor matematice , prin fundamentarea stiintifica a conceptelor , prin introducerea progresiva , gradata a limbajului matematic modern .

Alegerea acestei teme este motivata de importanta deosebita a întelegerii notiuni de operatie aritmetica bazata pe conceptul de numar natural .

Activitatea la clasa mi-a oferit posibilitatea sa constat ca uneori elevii din ciclul primar întâmpina greutati în însusirea notiunilor despre operatiile aritmetice . Am constatat ca pentru a oferi posibilitatea de însusire de catre toti elevi a unui minim de cunostinte si tehnici utile de lucru este necesar sa se tina seama de urmatoarele aspecte:

în toate formele de predare sa se respecte etapele dezvoltarii psihopedagogice ale copilului ;

trezirea interesului pentru aplicarea în practica a cunostintelor dobândite .

Pentru a-i învata pe elevi sa învet 858c27i e, pentru realizarea unui învatamânt activ formativ al matematicii , stilul de lucru, metodele si procedeele au o importanta deosebita .

Scopul activitatii matematice este de a-i exersa copilului intelectul , procesele de cunoastere , de a-l face apt sa descopere relatii abstracte pe baza situatiilor întâlnite în activitatea obisnuita .

Alegerea temei a fost determinata si de întrebarea : Ce metode putem folosi pentru a usura întelegerea notiunilor privind predarea-învatarea operatiilor aritmetice în învatamântul primar . Am constatat ca jocul didactic este o forma eficienta de lucru cu elevii din clasele I-IV .

În cadrul obiectului matematica , jocul didactic aduce varietate în exercitiul matematic , învioreaza lectia si ca urmare drumul spre deprinderi este mai sigur si mai placut .

Ipoteza de lucru si obiectivele cercetarii .

,,Cercetarea psihopedagogica este diferita de mai multe functii : explicatia praxiologica , predicativa , sistematizarea , referentiala , informationala etc .

Cercetarea poate lua forme variate , de la simpla observare dirijata la experimantarea de tip formativ si orice cercetare pedagogica este întreprinsa pentru dezvoltarea si perfectionarea continua a procesului de învatamânt . În initierea cercetarii am pornit de la convingerea ca exista o discrepanta uneori între eforturile ce se fac pentru realizarea unei calitati superioare de învatamânt si rezultatele care se obtin .

Întreaga activitate de documentare , convorbirile , dezbaterile si clarificarile rezultate contribuie la definitivarea problematicii cercetarii , adica a perspectivei teoretice pe care cercetatorul se decide sa o adopte pentru tratarea si aprofundarea problemei abordate . Astfel pe baza informarii bibliografice , a schemelor , modelelor explicative , a paradigmelor furnizate de lucrarile de referinta , cercetatorul adopta un cadru teoretic ce corespunde temei respective si expliciteaza propria problematica , redefineste cât mai bine obiectul cercetarii sale, perspectiva de abordare .

Practica pedagogica ofera nenumarate posibilitati de cercetare , deoarece ea presupune confruntarea cu o gama larga de probleme la care trebuie gasite sugestii , solutii pentru a fi rezolvate .

Porcesul formarii conceptului de numar natural se bazeaza pe notiunea de multime si introducerea operatiilor cu numere naturale si are la baza operasiile cu multimi de obiecte . Acestea constituie baza intuitiv-corecta pentru întelegerea de catre elevi a operatiilor cu numere naturale , cât si pentru sesizarea principiilor de baza dupa care se efectueaza calculul si proprietatile operatiilor .

În cercetarea efectuata s-a elaborat ipoteza ca jocul didactic , prin utilizarea si intregarea adecvata în lectiile de matematica , poate duce la cresterea eficientei învatarii notiunilor matematice si prin aceasta la un progres scolar al elevilor din ciclul primar .

În vederea demonstrarii acestei ipoteze mi-am propus declansarea unei cercetari psihopedagogice în care am folosit o serie de metode de cercetare : experimentul , observarea , testarea cunostintelor .

În cadrul cercetarii s-au urmarit urmatoarele obiective :

Cunoasterea trasaturilor psihice ale copiilor si stabilirea acestora ;

Integrarea optima a proceselor evaluative în activitatile matematice prin folosirea metodelor specifice ;

Analiza comparativa a datelor initiale si finale ;

Folosirea metodelor si descriptorilor drept criterii unice de masurare obiectiva a rezultatelor scolare la matematica ;

Evaluarea initiala a cunostintelor privind operatiile de adunare si scadere a numerelor naturale ;

Evaluarea finala a cunostintelor despre adunarea si scaderea numerelor naturale ;

Desprinderea unor concluzii.

CAPITOLUL I

CARACTERISTICI PSIHO-PEDAGOGICE ALE COPIILOR DE VÂRSTĂ sCOLARĂ MICĂ , CU IMPLICAŢII ÎN ÎNVĂŢAREA MATEMATICII

I.1. Particularitati psihologice ale copilului de vârsta scolara mica : semnificatia psihologica a contactului cu matematica .

Pavelcu V. sublinia : ,, Fiecare om , în acelasi timp seamana cu toti , seamana cu unii si nu seamana cu nimeni ."

Doi copii pot fi asemanatori, chiar tipici în ceea ce priveste caracteristicile generale de vârsta , dar extrem de diferiti în manifestarea concreta a acestora.

Deci, pe fondul general al particularitatilor de vârsta, îsi spun cuvântul particularitatile psiho-individuale . Dezvoltarea psihica nu are numai un caracter studial, ci un caracter individual, specific fiecarui individ .

De la nastere si pâna la maturitate , omul strabate un drum lung de dezvoltare . În decursul anilor , în viata copilului se produc transformari fizice si psihice însemnate . Acestea nu constau doar în adaosul de înaltime si greutate sau în simpla sporire a cunostintelor si deprinderilor copilului . Dezvoltarea copilului nu poate fi privita doar ca un proces de schimbari cantitative . Faptele arata ca în dezvoltarea psihica se produc si schimbari calitative importante .

Asadar prin dezvoltare trebuie sa întelegem în primul rând transformarile calitative, de natura fizica si psihica ce se produc în viata copilului . Dezvoltarea psihica a copilului consta , în primul rând, complcarea si adâncirea activitatii sale de cunoastere . Ea se caracterizeaza prin modificarea relatiilor sale cu cei din jur , prin schimbarea atitudinii sale fata de mediul înconjurator .

În stânsa legatura cu relatiile pe care le are copilul cu cei din jur , se dezvolta treptat viata sa afectiva, cu dezvoltare sentimentelor si atitudinilor fata de obiectele si fenomenele realitatii . Pornindu-se de la aceasta baza , se contureaza treptat trasaturile de caracter ale copilului, perfectionându-se si activitatea acestuia . La început, miscarile sale sunt raspunsuri simple , directe la stimulari externe si interne . Aceste acte se complica treptat , câstigând în precizie si coordonare .Putem spune ca directiile principale ale dezvoltarii psihice a copilului sunt : complcarea si adâncirea activitatii sale de cunoastere, transformarea vietii sale afective, a relatiilor sale fata de mediul înconjurator si perfectionarea activitatii în sensul dezvoltarii conduitei voluntare .

Copilul se dezvolta sub influenta educatiei si a conditiilor de viata . Actiunea mediului social si a educatiei, nu se desfasoara însa pe ,,teren '' gol . El se naste cu anumite dispozitii naturale, care reprezinta premizele dezvoltarii sale psihice . Aceste dispozitii mostenite nu contin însusiri psihice si aptitudini gata formate . Ele se formeaza si se dezvolta, pe baza dispozitiilor înnascute, în procesul activitatii, educatiei si instruirii .

Intrarea în scoala constituie un moment important în educatia si dezvoltarea copilului . El intra într-un cerc de relatii noi : cu învatatorul, cu elevii din clasa si sporadic cu colectivul scolii . Apar cerinte noi, copilul învata sistematic , cu sentimentul tot mai clar ca desfasoara o activitate serioasa , de importanta sociala . Modul cum îsi îndeplineste obligatiile de elev, defineste pozitia sa în scoala , în colectivul de clasa si în familie .

Cunoasterea profilului psihologic al scolarilor mici este de o mare importanta în abordarea strategiilor didactico-educative, în stilul de munca al cadrului didactic si în relatiile cu copiii.

Fiecare disciplina care se studiaza în scoala are menirea de a ,, construi'' si ,,reconstrui '' logic si progresiv în structurile mentale ale elevului un sistem de cunostinte stiintifice care sa se aproprie de logica stiinte respective .

Matematice este stiinta conceptelor celor mai abstracte, de o extrema generalitate . Ca ,,abstractiuni ale abstractiunilor'' ele se construiesc la diferite ,,etaje'' prin inductie , deductie , transductie .

Specificul gândirii copilului de vârsta scolara mica (mai ales în primele clase) se manifesta printr-o proprietate esentiala, anume aceea de a fi concret intuitiv . Asa cum arata J. Piaget, ne gasim în stadiul operatiilor concrete . Copilul gândeste mai mult operând cu multimi concrete .

În acest cadru teoretic se înscrie si cerinta ca proiectarea ofertei de cunostinte matematice la clasele mici sa ia în considerare formele si operatiile specifice gândirii copilului .

Gândirea este dominata de concret fiind specifica vârstelor între 6/7- 10/11 ani. Perceptia lucrurilor ramâne înca globala ,, vazul lor se opreste asupra întregului înca nedescompus ", lipseste dubla miscare rapida de disociere recompunere (H . Wallon) comparatia reuseste pe contraste mari , nu sunt sesizate starile intermediare . Domina operatiile concrete, legate de actiuni obiectuale, apare ideea de invariatie , de conservare (a cantitatii, volumului , masei etc.) . Se poate vorbi de puterea de deductie imediata ; copiii pot efectua anumite rationamente de tipul ,,daca ....., atunci , cu sprijin pe obiecte concrete sau exemple . De asemenea se remarca prezenta rationamentului progresiv, de la cauza la efect, de la conditii la consecinta .

Spre clasa a IV a (vârsta 10/11 ani ) putem întâlni , evident diferentiat si individualizat, ,,manifestari ale stadiului preformal, simultan cu mentinerea unor manifestari intelectuale situate la nivelul operatiilor concrete .(Aron I.1)

Caracteristicile acestui stadiu genereaza si unele optiuni metodologice bazate pe strategii destinate formarii si învatarii conceptelor matematice .

În acest sens , prioritate va avea nu atât stadiul strict delimitat în care se gasesc elevii din punct de vedere al vârstei, cât, mai ales , zona proximei dezvoltari a capacitatilor intelectuale ale acestora . Aceasta nu înseamna, cum afirma specialistii (Dottrens R. , Miliaret G. , D.P. Asubel 13) o situare exacta în stadiu si nici a ,,sari " în predare-învatare cu mult peste posibilitatile copiilor .

Esential este ca legalitatile constructiei psiho-genetice sa fie cunoscute, iar formarea notiuni si operatii mintale sa porneasca de la modele concrete .Lectura perceptiva este o realitate pentru construirea conceptelor si pentru formarea operativitatii matematicii, asa cum nevoia de exteriorizare sub forma unor actiuni sateriale sau materializate, fie cu obiecte, fie cu substitute ale acestora (modele, scheme grafice, bile, jetoane etc) reprezinta baza reala a materializarii actului mintal .

Toate acestea ne conduc la ideea ca gândirea logica la clasele mici nu se poate dispensa de intuitie, de operatiile concrete cu multimi de obiecte.

Înainte de a se aplica propozitiile, enunturile verbale, logica nitionala se organizeaza în planul actiunilor obiectuale, ale operatiilor concrete. De aceea, procesul de predare-învatare a matematicii în clasele I-IV trebuie sa însemne mai întâi efectuarea unor actiuni concrete, adica operatii cu obiecte, care se structureaza si se interiorizeza, devenind progresiv, operatii logice abstracte .

Formarea notiunilor matematice se realizeaza prin ridicarea treptata catre general si abstract, unde relatia între concret si logic se modifica în directia esentializarii realitatii .În acest proces trebuie valorificate diverse surse intuitive : experienta empirica a copiilor, matematizarea realitatii înconjuratoare, operatiuni cu multimi concrete de obiecte, limbaj grafic . Astfel, se pot ilustra notiunile de multime, apartenenta, incluziune, intersectie, reuniune s.a. cu obiecte reale (banci, caiete, carti ) si cu obiecte cunoscute de catre copii, (pasari, copaci ,flori e.t.c.). Însusirea caracteristica a obiectelor ce apartin multimii respective este intuita de copii, sesizata prin experienta lor spontana si nu determinata în mod precis. Au loc însa operatii de clasificare a obiectelor care au însusirea ce caracterizeza multimea respectiva si apartin acesteia.

În compararea multimilor prin procedeul formari perechilor (unu la unu) se poate face apel la carti, caiete , scaune (banci), elevi; pentru multimile cu,, tot atâtea elemente" se pot compara multimi ca : elevi-paltoane, ghiozdane-elevi s.a..Putem efectua cu elevii clasificari de genul : baieti-fetite = copii ,câine -pisica= animale domestice, vrabiute-rândunele =pasarele s.a.

Notiunile de relatii între multimi pot fi cunoscute de copii si în cadrul diferitelor ilustratii (tablouri, ilustratii de carte) prin care ei sunt condusi sa sesizeze notiunea sau relati respectiva în imaginile care reprezinta aspecte din viata (copii care se joaca cu masinute, cu mingi, cu iepurasi, catelusi).Referitor la aceasta problema J.Piaget afirma ca nu obiectele în sine poarta principiile matematice , operatiile cu multimi concrete .

Operatiile logice trebuie, de aceea cunoscute mai întâi în actiunile concrete cu obiectele si apoi interiorizate ca structuri operatorii ale gândirii .Elevul este pus sa efectueze operatii logice cu multimi de obiecte care poarta în ele legitati matematice (betisoare ,bile, riglete s.a.). Acest lucru se poate face la nivelul claselor I-IV, fara a recurge la terminologia utilizata în studiul structurilor matematice .Introducerea mai târziu a notiunilor de teoria multimilor (care se face începând cu clasa a V a)nu împiedica exersarea la clasele I-IV a structurilor logice necesare în conformitate cu intentia dezvoltarii lor ulterioare .

Materialul didactic cel mai potrivit pentru a demonstra cu multa exactitate si precizie multimile, relatiile dintre multimi ca baza a formari notiunii de numa natural si operatiile cu multimi, ca baza a operatiilor cu numere naturale, este constituit din truse. Datorita faptului ca atributul (caracteristica) dupa care se constituie multimile ca figuri geometrice sau piesele trusei ,,Logi II"este precis determinat (forma, culoare, marime, grosime), structurile logice se pot demonstra cu acesta în mod riguros matematic .De aceea, putem aprecia ca aceasta reprezinta materialul didactic concret cu cea mai bogata încarcatura logica, cu valentele cele mai mari în a-i ajuta pe copii sa înteleaga cu precizie si siguranta, relatiile dintre multimi, operatiile cu multimi. În operarea cu piesele jocurilor logice, copii se gasesc foarte aproape de operarea cu structuri logice .De aceea ,,comenzile " (instructiunile) învatatorului trebuie sa lase mai mult loc pentru independenta, initiativa si inventivitatea copilului (de exemplu, formati o multime din piese de aceeasi culoare, sau de aceeasi forma, sau de aceeasi forma si aceeasi culoare etc.) .

Reprezentarile grafice si limbajul grafic sunt foarte aproape de notiuni . Ele fac legatura între concret si logic, între reprezentare si concept care este o reflectare a proprietatilor relatiilor esentiale ale unei categorii de obiecte sau fenomene, între cele doua niveluri, interactiune este logica si continua .Ea este mijlocita de formatiuni mixte de tipul conceptelor figurative, al imaginilor esentializate sau schematizate care beneficiaza, prin generalitatea semnificatiilor purtate de apartenenta lor la reteaua conceptuala si prin impregnarea lor senzoriala, de aportul inepuizabil al concretului .

Imaginile mintale, ca modele partial generalizate si retinute în gândire într-o forma figurativa, de simbol sau abstracta, îl aproprie pe copil de logica operatiei intelectuale cu obiectele, procesele si evenimentele realitatii, devenind astfel sursa principala a activitatii gândirii si imaginatiei . Generate în mod continuu de interactiunea noastra cu lumea înconjuratoare, imaginile mintale se interpun între noile stimulari (cunostinte, operatii) si raspunsurile elevilor, mediind, în sensul cel mai larg al cuvântului, cunoasterea realitatii matematice .

Operatia de generalizare la care trebuie sa ajungem are loc atunci când elevul este capabil sa exprime prin semne grafice simple (puncte, linii, cerculete, figuri geometrice) ideea generala care se desprinde în urma operatiilor efectuate cu multimi concrete de obiecte . Semnul grafic evoca obiectele pe care le reprezinta ca element al multimii .Criteriul de apartenenta la o multime sau alta (culoare , forma , marime) a ramas doar în mintea elevului ca o structura logica .El exprima grafic fenomenul matematic pe baza întelegerii lui, a sesizarii esentialului, ceea ce înseamna de fapt pe baza definitiei lui .

Nivelurile de constructie prezentate mai sus nu se succed linear în formarea conceptelor matematice .Lafiecare nivel, pe masura ce ne apropiem de concept, exista o înbinare complexa între concretul ,, cel mai concret" si imagine, între senzorial si logic . De aceeea nu este vorba de o parcurgere rigida si strict liniara a acestor etape ci de organizare si dirijare rationala, metodica a relatiei intuitiv-logic adecvate conceptului respectiv, în strânsa conexiune cu cionditiile concrete în care se desfasoara activitatea didactica . Important este ca activitatea elevilor sa fie dirijata pe linia atingerii progresive a esentei conceptului respectiv. Reiese astfel mai clare conceptele :formarea multimilor , pe linia însusirii proprietatii caracteristice pe care trebuie s-o aiba elementele respective pentru apartine unei multimi, formarea notiunii de numar , pe linia clasei de echivalenta a multimilor echivalente, operatia de adunare, pe linia reuniunii multimilor disjuncte, care trebuie nu numai constatata pe un desen din manual, ci operata prin manevrarea obiectelor la niveluri diferite de concretul logic etc.

Multimile ne apar deci ca fiind produsul unor operatii mintale, în timp ce obiectele (elementele) din care sunt formate ele sunt obiecte fizice . De aceea, pe întreg parcursul formarii conceptelor de numar natural, de operatii cu numere naturale pe baza multimilor trebuie sa se realizeze îmbinarea între concret si logic, cu negarea dialectica, treptata, a concretului si asimilarea (interiorizarea) modelului (abstractiunii) respectiv .

I.2. Relatia de continuitate între gradinita si învatamântul primar.

Formare limbajului matematic.

Învatamântul prescolar, prima veriga a sistemului nostru de învatamânt, are menirea de a asigura pregatirea copiilor pentru activitatea scolara .Având un rol preponderent formativ, învatamântul prescolar dezvolta gândirea, inteligenta, spiritul de observatie ale copiilor, exersând operatiile de analiza, sinteza, comparatie, abstractizare si generalizare în cadrul jocurilor logico-matematice .

În gradinita copilul învata, asa cum se precizeza si în programa, sa formeze colectii-multimi de obiecte ; descopera proprietatile lor caracteristice, stabileste relatii între ele, efectueaza operatii cu ele . În cadrul jocurilor logico-matematice, copii sunt familiarizati cu unele notiuni elementare despre multimi si relatii .Facând exercitii de gândire logica pe multimi concrete ei dobândesc pregatirea necesara pentru întelegerea numarului natural si a aoperatiilor cu numere naturale pe baza multimilor (conjunctia, disjunctia, negatia , implicatia, echivalenta, ca fundamentând intersectia, reuniunea, complementara, incluziunea si egalitatea multimilor). În principal, acestea constau în exercitii de clasificare , comparare si ordonare a multimilor de obiecte .

Exercitiile de formare a multimilor dupa o însusire, apoi treptat, dupa doua sau mai multe însusiri (culoare, forma , marime, grosime) reprezinta adevarate exercitii de clasificare a obiectelor dupa un criteriu dat .

Compararea multimilor de obiecte îi ajuta pe elevi sa stabileasca , fara a utiliza numere, relatiile dintre multimi, care pot avea mai multe elemente decât multimea cu care se compara, mai putine sau tot atâtea elemente .

Exercitiile de ordonare e elementelor unei multimi , mai întâi dupa un model dat (grupa mica ), apoi dupa criteriile stabilite (forma, marime, culoare-grupa mijlocie) si , în final , dupa mai multe criterii (grupa mare), conduc la pregatirea copiilor pentru compararea numerelor si pentru întelegerea sirului numerelor naturale .

Prin activitatile cu continut matematic (grupare, ordonare, comparare, punere în corespondenta), copiii sunt antrenati în actiuni operatorii cu diferite materiale (obiecte, imagini schematice ale acestora si simboluri, cerc, linie, punct etc.).Acestea constituie o baza reala prin care se realizeaza dezvoltarea intelectuala a copiilor de natura sa optimizeze integrarea în clasa I, sa asigure pregatirea lor pentru învatarea matematicii.

Învatarea unei stiinte începe de fapt cu asimilarea limbajului ei notional .Studiul matematicii în maniera moderna, înca de la clasa I, urmareste sa ofere elevilor, la nivelul lor de întelegere, posibilitatea explicarii stiintifice a conceptului de numar natural si a operatiilor cu numere naturale. Daca întelegerea acestor notiuni se realizeza la nivelul rigorii stiintifice a matematicii, atunci si limbajul în care se exprima acest sistem de notiuni trebuie sa întruneasca rigoarea stiintifica .

Exista o strânsa legatura între continutul si forma (denumirea) notiunilor care trebuierespectata cu precadere în formarea notiunilor matematice. Orice termen (denumire) trebuie sa aiba acoperire în ceea ce priveste întelegerea continitului notional ; astfel, asemenea termeni apar cu totul straini de limbajul actic al copilului si , fie ca-i pronunta incorect, fie ca sub aspect sonor îi pronunta corect, dar îi lipsec din minte reprezentarile corespunzatoare, realizându-se astfel o învatare formala .

Toate stiintele opereaza cu un aparat notional care se învata o data cu "descifrarea" notiunilor respective . Limbajul matematic, fiind limbajul conceptelor celor mai abstracte si mai generale, se introduce la început cu unele dificultati . De aceea , trebuie asigurata mai întâi întelegerea notiunii respective, sesizarea esentei, de multe ori într-un limbaj cunoscut de copii, accesibil lor, facând unele concesii din partea limbajului matematic . Pe masura ce se asigura întelegerea notiunilor respective, trebuie reprezentata si denumirea lor stiintifica .

Deci, pe masura ce elevul avanseaza în interpretatrea corecta a notiunilor matematice se introduce si limbajul riguros stiintific .

Atentia care se impune este deci ca în introducerea unei notiuni sa se dea numai acele elemente pentru care exista posibilitatea reala a întelegerii de catre elevi . Esentiala este alegerea metodelor celor mai potrivite pentru atingerea acestui scop .La nivelul claselor I-IV descrierea bazata pe unele exemple si operatii concrete , urmata de o atenta abstractizare pâna la nivelul accesibil sunt cele mai indicate . Important este ca tot ceea ce se face sa fie în limitele care permit dezvoltarea ulterioara corecta a notiunilor si operatiilor matematice .

Logica didactica a matematicii se construieste tinând seama de particualritatile psihice ale celor care învata matematica .

În evolutia mentala a scolarului de calsa I, o contributie esentiala la statornicia planului simbolic abstract o are contactul cu unele notiuni matematice, cu conditia ca prin programul de instruire sa se întretina învatarea mecanica .

Pe fondul unor structuri de baza, pot fi proiectate o infinitate de constructii operationale particulare :

miscarea în ordine crescatoare si descrescatoare a sirului de numere naturale;

tehnica primelor doua operatii fundamentale în concentrul 0-10 si apoi în limitele concentre pâna la 100;

înbogatire nomenclatorului notional .

Astfel , afla ca unele numere sunt termeni, fac cunostinta cu proprietatile : asociativitatea si comutativitatea .

Exercitii de tipul : a-3=4, 7-a=2 cultiva flexibilitatea, ajuta la automatizarea si cresterea vitezei de lucru si stimuleaza descoperirea, întelegerea, judecata, rationamentul matematic .

Pentru evitarea învatarii mecanice, cunostintele matematice trebuie introduse ca acte asociate, fondate una pe alta si ilustrate una din alta, cu realizarea unei legaturi interne de continuitate între actiunea practica si cea teoretica .

Daca la clasa I modelul de învatare este cu precadere intuitiv, empiric, la clasa a II a se reduce intuitiv pâna la eliminare . Învatarea contine nu numai informatie mai multa, ci si multa metoda . Preocuparea pentru metoda, ca factor principal al crearii accesului elevului la gândirea matematica, este doar un început, pentru ca ponderea mare revine tot exercitiului, aplicatiei, ceea ce duce la un efect de consolidare a deprinderii de calcul , înaintea judecatii matematice .

Unul din momentele esentiale ale învatarii matematicii în clasa a III aîl constituie familiarizarea elevilor cu ordinele si clasele numerelor . Operatiile matematice fundamentale, însusite în clasa a II a , sunt solicitate sa fie lucrate în conditiile compartimentarii ordinale a numerelor . Acum sunt introdusi termeni fizici de baza : întinderea ,volumul , greutatea, durata, iar notiunile de geometrie întregesc setul sarcinilor care compun matematica la clasa a III a .

În clasa a IV a temele care îi introduc pe elevi în învatarea notiunilor de fractie, ca mod de redare a relatiei parte-întreg , ca si problemele tipice ofera bune ocazii de educare a gândirii matematice. Creste competenta cognitiva a elevului pentru sarcini din ce în ce mai complexe .Una din notele specifice ale învatarii o poate constitui calauzirea elevului spre reflexivitatea matematica bazata pe implementarea noului în unitate, cu reconsiderarea "stiutului" .

Învatarea matematicii este o activitate anevoioasa si uneori ,am întâlnit cazuri când elevul avea reactii negative, de respingere fata de acest obiect.

Motivatia învatarii în studierea aceste discipline de învatamânt am sustinut-o prin stimularea si mentinerea într-o stare activa a curiozitatii cognitive ale copiilor .

Am fructificat aceasta "dechidere" a personalitatii scolarilor mici spre nevoia de a afla, de a cunoaste, pentru a cultiva atasamentul tata de scoala si de învatatura si interesul pentru matematica .

I.3. Elemente de curriculum.

Termenul de curriculum este folosit din abundenta în literatura pedagogica, în textele de politica a educatiei, în mass-media, în limbajul comun. Semnificatiile induse întretin însa opinii aflate uneori în contradictie cu esenta curriculumului.

Fundamentele istorice ale curriculumului sustin clarificarea conceptului din perspectiva evolutiilor sale pedagogice si sociale, realizate în trei etape semnificative : premoderna, moderna, postmoderna.

În etapa premoderna (secolul XVII sfârsitul secolului XIX), curriculumul este înteles în sens traditional , doar ca document oficial care programeaza continutul studiilor în cadrul sistemului de învatamânt .

În etapa moderna, curriculumul, în acceptia de continut, este raportat la experienta de învatare a elevului . Astfel poate fi depasita pedagogia traditionala în cadrul careia manualul si profesorul se întrec sa prezinte copilului obiectul de studiu asa cum apare acesta specialistului .

În etapa postmoderna sunt afirmate principiile de baza ale curriculumului, exprimate prin întrebari-problema cu valoare metodologica superioara :

Ce scopuri si obiective trebuie sa realizeze institutia scolara ;

Ce experiente de educatie/instruire pot fi oferite pentru atingerea acestor scopuri si obiective ;

Cum pot fi organizate aceste experiente pentru atingerea scopurilor si a obiectivelor propuse ;

Cum poate fi determinat nivelul de realizare a scopurilor si a obiectivelor propuse.

Aceste principii vor marca evolutia curriculumului ca model rational de proiectare (obiective-experiente de învatare/continuturi si metodologie-evaluare /cu functie de reglare -autoreglare continua a activitatii de educatie/instruire).

Dupa 1970, curriculumul , notiune pedagogica de mare generalitate , are o extindere " valabila într-un sens cât mai larg posibil", la toate nivelurile sistemului si ale procesului de învatamânt . El reprezinta "un proiect educativ care defineste .a) telurile , scopurile si obiectivele unei actiuni educative ; b) caile, mijloacele si activitatile folosite pentru a atinge aceste scopuri; c)metodele si instrumentele pentru a evolua în ce masura actiunea a dat roade " Cretu Carmen (8).

Conceptul de curriculum cunoaste definitii care acopera o realitate pedagogica extrem de extinsa sau de restrânsa în raport de sistemul de referinta si de evolutia stiintelor educatiei într-un timp si un spatiu determinat din punct de vedere istoric.

Depasirea limitelor care apar în definirea curriculumului, presupune regândirea acestui concept pedagogic fundamental, aplicabil la scara întregului sistem si proces de învatamânt. Ccurriculumul este ansamblul complex si evolutiv de reguli de desfasurare pedagogica a unei actiuni de educatie sau de formare realizata la diferite niveluri de operationalizare .Acest ansamblu este definit , în mod esential prin :

- finalitati, obiectivele generale ale actiunii si / sau efectele asteptate pe terenul traversat de acesta;

- continuturile-materii, obiectivele, capacitatile si / sau competentele de dezvoltat la cei care învata ,

- metodele pedagogice ;

- modurile de gestiune aprocesului , inclusiv modul de relationare între actorii educatiei/instruirii,

- articularea cu contextul organizational sau al mediului înconjurator ,

- modalitati de evaluare a performantelor celor care învata ."

Literatura pedagogica de ultima generatie vorbeste despre o stiinta a curriculumului, cu o viziune globala care trebuie construita special pentru realizarea deplina a obiectivelor la nivelul clasei de elevi" .

"Noua stiinta" confirma principiile de baza ale curriculumului lansate la jumatatea secolului XX, la nivelul modelului rational . Dintre principiile dezvoltate de "noua stiinta a curriculumului " putem enumera :

a) explicarea clara a scopurilor cu valoare motivationala (teoretica si practica) pentru toti elevii ;

b) construirea clara si simpla a curricumului (accent pe structura cunoasterii, pe identificarea elementelor esentiale) în raport cu scopurile propuse;

c) prezentarea cunoasterii stiintifice dintr-o perspectiva istorica si actuala, teoretica si practica (prin studii de caz relevante pedagogic si social );

d) integrarea tehnologiilor si a aplicatiilor în structura stiintei;

e) întelegerea stiintei prin rezolvarea de probleme si situatii problema bazate pe aplicarea cunostintelor solide (conceptelor fundamentale cu valoare metodologica superioara );

f) stimularea profesorului (si implicit a elevului în directia promovarii unei game variate de metode si tehnici de instruire (respectiv de învatare);

g) promovarea strategiilor , metodelor si tehnicilor (procedeelor) de evaluare care asigura concentrarea profesorului asupra aptitudinilor elevilor .

În ultima instanta , esentiala este cunoasterea si valorificarea deplina a capacitatii/aptitudinii elevului de învatare a stiintei la nivel profund, în termeni de explicare si de întelegere, de fixare normativa si de interpretare metodologica de dezbatare convergenta si divergenta (de abordare a controverselor, solutiilor discutabile, inovatiilor posibile etc.) .

Cele sapte principii identificate sunt raportabile la structura modelului rational bazat pe definirea finalitatilor si selectarea optima , în consecinta , a componentelor care vizeaza continuturile-metodologia-evaluarea . Ceea ce pare distinct tine de "punctul de vedere constructivist" care trebuie adoptat (si adaptat ) într-un (la un) context global .

Dechiderea curricumului fata de valorile culturii globale si locale , universale si nationale, fata de traditiile si inovatiile pedagogice, genereaza chiar " o stiinta radicala a curricumului " care vizeaza în mod explicit .

a) transmiterea culturii stiintifice , la nivelul unor ( sau prin intermediul unor) circuite de comunicare pedagogica , construite (perfectionate) permanent prin diferite mijloace de retroactiune (conexiune inversa) externa si interna;

b) dezvoltarea la elevi a capacitatii cognitive necesare pentru întelegerea , aplicarea, analiza-sinteza, evaluarea critica a informatiilor în contexte situationale deschise ,

c) formarea-dezvoltarea la elevi a capacitatilor de evaluare si de auto-evaluare obiectiva pe criterii de maxima rigurozitate ,

d) formarea-dezvoltarea aptitudinilor elevilor de participare la (re) constructia sociala prin valorizarea cunostintelor stiintifice si a tehnologiilor dobândite , în perspectiva modelului cultural al societatii postmoderne informationale .

(Re)constructia curriculumului va avea în vedere personalitatea elevului în ansamblul sau : "un entuziasm pentru studiul stiintei si încrederea în folosirea acesteia" . Este miza unei pedagogii a succesului , propriei paradigme curriculumului, în orice varianta dezvoltata mai veche sau mai noua .

Programa scolara de matematica stabileste continutul obiectului . Continuturile sunt mijloace prin care se urmareste atingerea obiectivelor cadru si a obiectivelor de referinta propuse . Unitatile de continut sunt organizate fie tematic, fie în conformitate cu domeniile constituitive ale diverselor obiecte de studiu .

Realizarea programei este obligatorie pentru învatatori . În parcurgerea ei trebuie pastrat un ritm reflectat de planul calendaristic ,pentru fiecare clasa si disciplina .

Rolul învatatorului care preda nemijlocit la clasa este foarte, deoarece succesiunea unei teme date dupa planificarea proprie sau în catedra , procedeele didactice cele mai rodnice, mai stimulative se creaza si se verifica în procesul predarii.

Manualele scolare vor fi construite curricular în masura în care programa scolara este construita curricular . Manualele alternative de matematica sunt utile în masura în care au o baza stabila a obiectivelor si a continuturilor fundamentale . Aceasta va permite alegerea unor cai diferite de organizare a învatarii, evaluare alternativa, autoînvatare .

Manualul scolar reprezinta mijlocul de baza folosit în procesul de învatamânt activ cât si în afara acestuia, fiind principalul material bibliografic al elevului . El reprezinta detaliat continutul programelor scolare .Functia principala a manualului este aceea de informare a elevului, este mijloc de baza al studiului sau, care îi da posibilitatea de a învata în continuare . De aceea autorii de manuale trebuie sa tina seama ca acestea ar trebui nu numai sa-l ajute pe elev sa tnvete matematica, dar sa-l obisnuiasca în acelasi timp cu munca individuala cu cartea de matematica .

Unele teme sunt organizate a se preda în "spirala" care consta în reântoarcerea la acelasi continut, de fiecare data pe o treapta superioara . Acest mod de prezentare corespunde sistemului concentric propri-zis sau concentric calitativ si sistemului concentric cantitativ sau concentric liniar .

Sistemul concentric cantitatic "desemneaza modul de organizare a cunostintelor în programe de învatamânt, manuale si lectii astfel încât notiunile se însusesc în etape prin reluari, restructurari si reinterpretari pâna la formarea lor completa si corecta . În acest mod sunt planificate notiunile despre arii si volume care se predau si învata în clasele primare cât si în gimnaziu si liceu .

Sistemul concentric cantitativ este modul de organizare a cunostintelor în programe scolare, manuale si lectii care constau în reluarea adaugita si detaliata a materiei parcurse anterior, reluare reclamata nu atât de dificultatea întelegerii notiunilor, ci mai ales de nevoia largirii cunostintelor an succesiunea claselor si treptelor scolare ".Programele scolare trec printr-un proces complex de elaborare si revizuire an viziunea curriculara, care presupune o proiectare în interactiunea lor a obiectivelor, activitatilor de învatare si a principiilor si metodelor de învatare . Noile planuri cadru de învatamânt stimuleaza de astfel prin existenta curricumului le decizia scolii, inovatia curriculara locala la nivelul fiecarui cadru didactic si la nivelul fiecarei catedre .

Noul curriculum scolar , prin conceperea lui ca echilibru între curriculum nucleu si curriculumul la decizia scolii, contribuie în mod specific la descentralizarea si flexibilizarea deciziilor curriculare la nivelul unitatilor scolare .Programele scolare favorizeaza o noua viziune dideactica în elaborarea manualelor scolare, care prin rolul lor de instrument curricular si didactic orienteaza într-o mare masura demersul de predare-învatare la clasa, inclusiv evaluarea elevilor si stimularea unei motivatii sustinute pentru învatare .

Actualele programe scolare subliniaza importanta rolului reglator al obiectivelor pe cele doua niveluri de generalitate : obiective cadru si obiective de referinta.

Proiectarea Curricumuluio de matematica a fost ordonata de principiile :

asigurarea continuitatii la nivelul claselor si ciclurilor ;

actualitatea informatiilor predate si adaptarea lor la nivelul de vârsta al elevilor ;

diferentierea si individualizarea predarii-învatarii ;

centrarea pe aspectul formativ ;

corelatia transdisciplinara si interdisciplinara ;

delimitarea unui nivel obligatoriu de pregatire matematica a tuturor elevilor si profilarea posibilitatilor de avensare în învatare si de obtinerea de noi performante .

Pentru realizarea scopului studierii matematicii în scoala , curricumul contine "Oobiective generale ale predarii-învatarii matematicii" .Ele deriva din obiectele pe arie curriculara "Matematica si stiintele" , servesc drept finalitati ale învataturii la sfârsitul ciclului scolar si au un grad foarte înalt de generalitate si de complexitate . Obiectivele generale sunt clasificate în categorii de cunostinte, capacitati si atitudini care se structureaza prin disciplina scolara Matematica . Aceste obiective servesc drept surse de elaborare a obiectivelor cadru , a obiectivelor de referinta . Totodata ele orienteaza educatorul în elaborarea obiectivelor operationale si a celor de evaluare .

Scopul studierii matematicii în scoala este întelegerea mai aprofundata a conceptelor , a procedurilor de calcul, a terminologiei . În cadrul studierii matematicii vor fi dezvoltate capacitatile de explorare-investigare, interesul si motivatia pentru studiul si aplicarea matematicii în contexte variate . Învatarea matematicii în scoala urmareste constientizarea naturii matematicii, pe de o parte, ca o activitatede rezolvare a problemelor, bazata pe un sistem de capacitati , cunostinte ,procedee, iar pe de alta parte, ca disciplina dinamica , strâns legata de viata cotidiana, de rolul ei în stiintele naturii, în tehnologii si în stiintele sociale .

Cadrul conceptual al curricumului este determinat de modelul de învatare structural cognitiv ce propune o noua paradigma pentru învatarea matematicii .Ea vizeaza formarea de structuri ale gândirii specifice matematicii. Aceasta prevede predarea de concepte , adica entitati structurate care cuprind definitii, teoreme , reguli , dar mai ales un mod de gândire propriu .Operatiile mentale si informationale de studiu sunt proiectate în obiectivele cadrul si cele de referinta. O astfel de aplicare se realizeaza pe nivele de abstractizare , adica se organizeaza activitati în plan obiectual (cu obiecte), în plan simbolic (cu simboluri neconventionale), apoi cu simboluri conventionale , în plan verbal si în plan mental interiorizat . Se fac permanent treceri de la o treapta de abstractizare la alta .

Studiul matematicii în învatamântul primar are ca scop sa contribuie la formarea si dezvoltarea capacitatilor de a reflecte asupra lumii, de a formula si rezolva probleme pe bazarelationarii cunostintelor din diferite domenii, precum si la înzestrarea cu un set de competente , valori si aptitudini menite sa asigure o cultura generala optima .

Trecerea sistematica de la învatamântul instructiv la cel de modelare a capacitatilor intelectului, ca si noua viziune asupra didacticii discipline Matematica, au impus necesitatea elaborarii unui curriculum de matematica pentru învatamântul primar ca o continuare a curriculumului pentru învatamântul prescolar si ca o baza aînvatamântului gimnazial .Învatamântul matematic va scoate an relief valorificarea potentialului creativ al elevului .

Proictarea Curricumului de matematica a fost ordonata de principiile :

asigurarea continuitatii la nivelul claselor si ciclurilor ;

actualitatea informatiilor predate si adaptarea lor la nivelul de vârsta al elevilor ;

diferentierea si individualizarea predarii-învatarii ;

centrare pe aspectul formativ ;

corelatia transdisciplinara-interdisciplinara (esalonarea optima a continuturilor matematice corelate cu disciplinele reale pe arii curriculare asigurându-se coerenta pe verticala si orizontala) .

În ciclul primar, matematica a ramas si va ramâne una din disciplinelle de baza . Elevii îsi însusesc notiuni elementare cu care opereaza pe tot parcursul vietii . scolarilor li se formeaza unele aptitudini si abilitati ale gândirii, pe lânga deprinderile de calcul si de rezolvare a preblemelor .

În planul de învatamânt, la clasele I-IVV, studiului matematicii îi sunt afectate 4 ore saptamânal pentru fiecare clasa avându-se în vedere ca, în ciclul primar se formeaza notiunile matematice elementare cu care copilul va opera pe tot parcursul vietii si pe care se cladeste antregul sistem al învatamântului matematic, ca acum se formeaza " instrumentele" mentale si abilitati ale gândirii.

Studiul matematicii în scoala primara îsi propune sa asigure pentru toti elevii formarea competentelor de baza vizând :calculul aritmetic, notiuni intuitive de geometrie, masurare si masuri .

În ansamblul sau, conceptia în care a fost construita noua programa de matematica vizeaza urmatoarele:

schimbari în abordarea continuturilor ;

● trecerea de la o aritmetica teoretica la o varietate de contexte problematice care genereaza aritmetica ;

- schimbari în ceea ce se asteapta de la elev ;

● trecerea de la aplicarea unor algoritmi la folosirea de strategii în rezolvarea de probleme ;

- schimbari de învatare ;

● trecerea de la memorizare si repetare la exploatare-investigare ;

- schimbari de predare ,

● trecarea de la ipostaza de transmitator de informatii a învatatorului la cea de organizator al unor activitati variate de învatare pentru toti copiii, în functie de nivelul si ritmu propriu de dezvoltare al fiecaruia ,

- schimbari de evaluare ;

● trecerea de la subiectivismul si rigiditatea notei la transformarea evaluarii într-un mijloc de autoapreciere si stimulare a copilului ;

Acestea impun ca învatatorul sa-si schimbe în mod fundamental orientarea în activitatea la clasa. (Lupu Costica 21)

Capata mai putina importanta :

● memorarea de reguli si socotitul ,

● problemele / exercitiile cu solutii sau raspunsuri unice ;

● matematica facuta cu "creionul si hârtia", respectiv "creta si tabla ";

● activitatea profesorului si învatatorului ca transmitator de cunostinte adresate unui elev care recepteaza pasiv si lucreaza singur ;

● evaluarea cu scopul catalogarii copilului .

Devine mult mai importanta :

● activitatea de rezolvare de probleme prin tatonari, încercari, implicarea activa în situatii practice, cautarea de solutii dincolo de cadrul strict al celor învatate ;

● formularea de întrebari , analiza pasilor de rezolvare a unei probleme, argumentarea deciziilor luate în rezolvare ;

● utilizarea unei varietati de obiecte care trebuie manipulate în procesul învatarii ;

● activitatea profesorului si a învatatorului în calitate de persoana care faciliteaza învatarea si îi stimuleaza pe copii sa lucreze în echipa ;

● evaluarea ca parte integranta a instructiei, cu rol stimulator-dinamizator în activitatea didactica .

Programa de matematica pentru învatamântul primar îsi propune sa transforme toate aceste idei în realitati ale practicii scolare prin intermediul componentelor sale : obiective cadru, obiective de referinta, activitati de învatare cu continuturi si standarde de performanta .

Obiectivele cadru au un grad ridicat de generalitate si complexitate si marcheaza evolutia copilului de-a lungul întregului ciclu primar asa cum reiese din actuala programa scolara :

Cunoasterea si utilizarea conceptelor specifice matematicii ;

Dezvoltarea capacitatilor de explorare/investigare si rezolvare de probleme ;

Formarea si dezvoltarea capacitatii de a comunica utilizând limbajul matematic ;

Dezvoltarea interesului si a motivatiei pentru studiul si aplicarea matematicii în contexte variate .

Obiectivele cadru exprima faptul ca scopul perdarii/învatarii matematicii în scoala primara nu se mai limiteaza la însusirea notiunilor specifice si la cunoasterea procedurilor de calcul .Se urmareste în egala masura stimularea capacitatii copilului de a explora notiuni si concepte necunoscute , de a experimenta , de a-si dezvolta posibilitatile de comunicare, se urmareste formarea unor atitudini si calitati personale în raport cu acest domeniu de studiu .

Obiectivele de referinta masoara progresia în cahizitia de cunostinte si capacitati . Ele au un nivel de generalitatecare permite perceptia sinetica a întregului demers didactic aferent unui an de studiu.

Aceste obiective cadru si de referinta se regasesc în programele scolare ale fiecarei clase . Astfel , la clasa I elevii vor învata sa scrie, sa citeasca, sa compare si sa ordoneze numerele naturale de la 0 la 100, vor efectua operatii de adunare si de scadere în concentrul 0-30 fara trecere peste ordin învatând totodata sa rezolve probleme care presupun o singura operatie din cele învatate, sa formuleze oral exercitii si probleme cu numere de la 0 la 30 . În clasa a II a se vor relua cunostintele despre numerele naturale si operatii cu acestea largindu-se concentrul de lucru cu numere naturale pâna la 1000. În aceasta clasa elevii se vor familiariza cu notiuni : termen, suma, "cu atât mai mult", "cu atât mai putin" , cu unele dintre proprietatile adunarii (comutativitatea, asociativitatea, element neutru ) fara terminologie . Deasemeni elevii îsi vor însusi notiunile despre aflarea unui numar necunoscut în cadrul unei relatii de tipul ? + a = b ; ? - a = b sau a + ? = b; a - ? = b .

În clasa a III a adunarea si scaderea numerelor naturale se va realiza în intervalul de la 0 la 10 000 . Elevii vor opera cu termeni : descazut, scazator , suma, termen " cu atât mai mult", "cu atât mai putin", vor evidentia unele proprietati ale adunarii (comutativitatea, asociativitatea, element neutru ) cu ajutorul obiectelor si al reprezentarilor, faar a folosi terminologia . Ca o noutate în clasa a III a se introduc alte doua operatii cu numere naturale mai mici ca 100 : înmultirea si împartirea .

În cadrul acestui capitol se propu urmatoarele teme :

● Înmultirea numerelor naturale folosind adunarea repetata de termeni egali ;

● Înmultirea numerelor scrise cu o singura cifra ;

● Terminologia specifica : factor, produs , "de atâtea ori maimult", dublu , triplu ;

● Tabla înmultirii ;

● Evidentierea unor proprietati ale înmultirii (comutativitatea, asociativitatea, element neutru, distribuitivitatea fata de adunare sau scadere) cu ajutorul obiectelor si al reprezentarilor, fara a folosi terminologia ;

● Ordinea efectuarii operatiilor ;

● Împartirea numerelor neturale folosind scaderea repetata si relatia cu înmultirea ;

● Terminologia specifica : deâmpartit, împartitor, "de atâta ori mai putin", jumatate, treime, sfert ;

● Tabla împartirii dedusa din tabla înmultirii ;

● Diviziunea ale unui întreg : jumatate, sfert, a treia parte, a zecea parte, reprezentari prin desene ;

● Aflarea unui numar necunoscut în cadrul unei relatii de tipul : ? x c = d , ? : c = d , unde c ≠ 0 , d este multiplu al lui c , cuprins în intervalul numerelor naturale 0-100 ;

● Ordinea efectuarii operatiilor si folosirea parantezelor rotunde .

Dupa ce elevii îsi însusesc înmultirea în cocentrul 0-100 aceasta se va extinde si în intervalul 0-1000 . În cadrul acestui capitol se propun urmatoarele teme .

● Înmultirea cu o suma sau diferenta ;

● Înmultirea cu 10 sau 100 ;

● Înmultirea unui numar natural de doua cifre si de trei cifre cu un numar de o cifra, folosind adunarea repetata, grupari de termeni, reprezentari ;

● Împartirea unei sume sau diferente la un numar de o cifra ;

● Împartirea la 10 sau 100 ;

● Împartirea unui numar natural mai mic decât 100 sau 1000 la un numar de o cifra, folosind scaderea repetata, grupari de termeni, reprezentari .

În clasa a IV a se reiau cunostintele despre numerele naturale si despre operatiile cu acestea ( adunare, scadere, înmultire, împartire) .Ca elemente noi sunt introduse : înmultirea cu mai multi factori, împartirea cu rest; relatia dintre deîmpartit, împartitor ,cât, conditia restului; împartirea la un numar de doua cifre diferut de zero; ordinea efectuarii operatiilor si folosirea parantezei .

Tot în clasa a IV a elevii se familiarizeaza cu notiunea de fractie . În cadrul acestui capitol elevii sunt familiarizati cu notiunile de : fractii, fractii egale, reprezentari prin desene, fractii echiunitare, subunitare, supraunitare, compararea fractiilor, adunarea si scaderea fractiilor cu acelasi numitor, aflarea unei fractii dintr-un întreg .

Pe lânga toate aceste cunostinte referitoare la operatiile aritmetice, elevii sunt "învatati" sa opereze cu aceste cunostinte, sa le foloseasca în rezolvarea problemelor de diverse tipuri . În acelasi timp cunostintele referitoare la operatiile aritmetice sunt folosite si în predarea cunostintelor de geometrie sau despre unitatile de masura (unitati de masurat lungimea : metrul, multipli, submultipli, transformari ; unitati de masurat capacitatea : litrul, multipli, submultipli, transformari ; unitati de masurat masa :kilogramul, multipli, submultipli, transformari ; unitati de masura pentru timp : minutul, ora, ziua, saptamâna, luna, anul, deceniul, secolul, mileniul ; monede si bancnote .

Standardele curriculare de performanta ofera criterii generale de evaluare, din perspectiva programei, la finalul scolii primare.

Întrucât activitatile de învatare sunt numai orientative si tin într-o masura mai mare de metoda didactica folosita, ele lasa libertatea creativitatii cadrului didactic .

Clasele I si a II a fac parte din ciclul achizitiilor fundamentale . Acesta acopera grupa pregatitoare a gradinitei urmata de clasele I si a II a, având ca obiective majore acomodarea copilului la cerintele sistemului scolar si alfabetizarea initiala . Acest ciclu curricular vizeaza :

● asimilarea elementelor de baza ale principalelor limbaje conventionale (scris, citit, calcul aritmetic) ;

● stimularea copilului în vederea perceperii , cunoasterii si stapânirii mediului apropiat ;

● stimularea potentialului creativ al copilului , a intuitiei si a imaginatiei ;

● formarea motivarii pentru învatare, înteleasa ca o activitate sociala .

Clasele a III a si a IV a fac parte din ciclul curricular de dezvoltare . Aceasta acopera clasele a III a-IV a si are ca obiectiv major formarea capacitatilor de baza necesare pentru continuarea studiilor . Ciclul de dezvoltare vizeaza :

● dezvoltarea achizitiilor lingvistice si încurajarea folosirii limbi române, a limbii materne si a limbilor straine pentru exprimarea în situatii variate de comunicare;

● dezvoltarea unei gândiri structurate si a competentei de a aplica în practica rezolvarea de probleme ;

● familiarizarea cu o abordare pluridisciplinara a domeniilor cunoasterii ;

● constuirea unui set de valori consonante cu o societate democratica si pluralista ;

● încurajarea talentului, a experientei si a expresiei în diferite forme de arta,

● formarea responsabilitatilor pentru propria dezvoltare si sanatate ;

● formarea unei atitudini responsabile fata de mediu .

Aceste obiective se transforma în recomandari si pot modela activitatea învatatorului la clasa, inclusiv prin prisma programei de matematica .

Spre deosebire de etapa anterioara , centrata pe explorare, intuire, verificarea calculelor cu ajutorul obiectelor, în ciclul curricular de dezvoltare se urmareste ca învatatorul sa-i ajute pe elevi sa înteleaga procedura de calcul si mecanismul din spatele ie, mergând pâna la a-i permite elevului sa foloseasca propiile metode de calcul ce conduc la obtinerea rezultatului corect . Pe masura ce copilul exerseaza , ajunge sa interiorizeze procedeul de calcul optim, care este cel algoritmizat , permitând copilului sa mearga în ritmul sau propiu si sa renunte la utilizarea obiectelor sau a reprezentarilor nu mai devreme decât în momentul când el însusi le considera un balast greoi si nefolositor, se câstiga enorm pentru elev în plan formativ, iar acesta va deveni capabil de salturi spectaculoase în achizitia de cunostinte si capacitati .

Începând din anul scolar 1998 în România , Curriculumul National cuprinde :

●Curriculumul National pentru învatamântul obligatoriu .Cadrul de referinta

(document reglator care asigura coerenta componentelor sistemului curricular, în termeni de procese si de produse );

● Planurile cadru de învatamânt pentru clasele I-XII , document care stabileste: ariile curriculare, obiectele de studiu si resursele de timp necesare abordarii acestora;

● Programele scolare, care stabilesc obiectivele cadru, obiectivele de referinta, exemple de activitati de învatare, continuturile învatarii, precum si standardele de performanta prevazute pentru fiecare disciplina existente în planurile cadru de învatamânt ;

● Ghidurile, normele metodologice si materiale suport care descriu conditiile de aplicare si de monitorizare ale procesului curricular ;

● Manuale alternative .

În elaborarea Planului-cadru de învatamânt au fost avute în vedere urmatoarele principii didactice :

Principiul selectiei si al ierarhizarii culturale în vederea stabilirii disciplinelor scolare, precum si gruparea si ierarhizarea acestora pe arii curriculare pentru întregul învatamânt preuniversitar ;

Principiul functionalitatii care, coroborat cu o serie de strategii de organizare interna a curriculumului a condus la structurarea procesului de învatamânt în ciclurile primare ;

Principiul coerentei care vizeaza caracterul omogen al parcursului scolar . Acest principiu are în vedere gradul de integrare orizontala si verticala a ariilor curriculare în interiorul sistemului iar în cadrul acestora, a obiectelor de studiu . Principiul coerentei vizeaza în esenta raporturile procentuale atât pe orizontala cât si pe verticala între ariile curriculare, iar în cadrul ariilor pe discilpine ;

Principiul egalitatii sanselor are în vedere asigurarea unui sistem care da dreptul fiecarui elev în parte de a-si valorifica la maximum potentialul de care dispune . Aplicarea acestui principiu impune : obligativitatea învatamântului general si existenta trunchiului comun, în masura sa asiguure elevilor accesul la "nucleul" fiecarei componente a parcursulsui scolar . Respectarea principiului egalitatii sanselor impune garantarea pentru fiecare elev, un numar de ore ale trunchiului comun, a unui nivel optim acceptabil de cunostinte si capacitati ;

Principiul descentralizarii si al flexibilitatii vizeaza trecerea de la învatamântul pentru toti la învatamântul pentru fiecare . Acest lucru poate fi realizat prin descentralizare curriculara . Numarul total de ore alocat prin planurile-cadru vizeaza între un minim si un maxim . Planurile-cadru prevade de asemenea pentru majoritatea obiectelor de studiu o plaja orara ce presupune un numar de ore minim si unul maxim ;

Principiu racordarii la social având drept consecinta asigurarea unei legaturi optime între scoala si comunitate, între scoala si cerintele sociale ;

Principiul descongestionarii programului scolar al elevilor, da posibilitatea de a concepe programele scolare în raport cu numarul minim de ore pe discipline (trunchiul comun ).

Curriculum National cuprinde doua segmente :

○ Curriculum nucleu cuprinde numarul minim de ore la fiecare disciplina obligatorie prevazuta în planul-cadru . El este general obligatoriu pentru toti elevii , asigurând totodata egalitatea sanselor pentru toti elevii den tara . Reprezinta unicul sistem de referinta pentru diferitele tipuri de evaluari nationale .

○ Curriculum la decizia scolii (C.D.S.) acopera diferenta de ore dintre curriculum nucleu si numarul maxim de ore pe saptamâna pe discilpine si ani de studiu .

Standardele curriculare asigura conexiunea dintre curriculum si evaluare. Pe baza lor se vor elabora nivelurile de performanta ale elevilor, precum si testele de evaluare. Standardele constituie o categorie curriculara de baza, situându-se alaturi de finalitatile pe sistem si pe ciclurile de scolaritate, dar si alaturi de curriculumul de baza.

Pe parcursul scolii primare , planul-cadru prevede la matematica un trunchi comun de 3 ore pe saptamâna .Acesta poate fi extins prin consensul agentilor educationali implcati . învatatori, parinti, elevi, conducerea scolii, la 4 ore pe saptamâna.

Repartizarea materiei in cadrul trunchiului comun are în vedere asigurarea pentru toti elevii a unui nivel optim acceptabil de competente si capacitati. În cele 3 ore ale trunchiului comun se poate opta, în functie de particularitatile clasei de elevi, fie pentru curriculum nucleu (ce include partea obligatorie a programei) , fie pentru curriculum extins (ce include, alaturi de partea obligatorie secvente facultative, marcate cu litere cursive în programa). De asemenea, în cazul alegerii a 4 ore pe saptamâna , se poate opta pentru curriculum nucleu sau pentru curriculum extins.

În acest context, învatatorul are un grad mai mare de libertate de decizie, dar în acelasi timp si de raspundere, în alcatuirea schemei orare, în functie de resursele umane si materiale de care dispune.

I.4. Strategia didactica si dimensiunea formativa a predarii-învatarii matematicii.

Orientarea proiectarii didacticii pe evidentierea strategiilor de predare-învatare este binevenita mai ales în contextul actual al modificarilor de ordin cantitativ si calitativ din programele scolare prevazute de Noul Curriculum National la toate nivelurile de scolaritate . Acesta pune accent pe formarea modurilor de a gândi, pe elaborarea strategiilor proprii de învatare si rezolvare de probleme, pe dezvoltarea capacitatilor intelectuale la elevi . De aceea cadrului didactic trebuie sa-i fie foarte clar ce strategie optima de predare trebuie sa adopte pentru a sprijini elevul în realizarea obiectivelor si pentru a capate în timp deprinderi intelectuale superioare organizate (strategii cognitive).

Esential în instruirea elevului este crearea situatiilor de învatare directionate de un obiectiv, în cadrul carora elevul îsi elaboreaza strategiile de abordare a problemelor.

Termenul de strategie a aparut initial în teoria si practica militara, unde se întâlnea sub denumirea de plan strategic; din punct de vedere tehnic notiunea se asociaza proceselor care prezinta un anumit grad de nedeterminare, situatiilor de natura competitiva sau conflictuala în cadrul carora apar factori ce se opun realizarii scopurilor intentionate . Ulterior termenul a capatat o semnificatie mai larga ce nu implca în mod necesar "opnentul", ci producerea eficienta a obiectului .

Dupa Neacsu Ioan (23), notiunea vizeaza "un sistem de operatii cu o finalitate bine determinata însotit de specificarea conditiilor de desfasurare si actiune . Ea reprezinta în esenta o actiune decompozabila într-o suita de decizii-operatii , fiecare decizie asigurând trecerea la secventa urmatoare pe baza verificari informatiilor dobândite în etapa anterioara " .În alta acceptiune semantica, în sens general, strategia se poate defini ca un ansamblu de procese si operatii sau procedee si metode orientate spre producerea unuia sau mai multor obiecte determinate . Actiunile implcate trebuie sa satisfaca anumite conditii de coerenta interna, compatibilitate si complementaritate a efectelor.

La nivelul macro (pedagogia sistemelor) actioneaza strategia pedagogica formata din ansamblul deciziilor privind desfasurarea cercetarii pedagogice, a politicii învatamântului si a procesului de învatamânt . Strategia procesului de învatamânt vizeaza operatia de proiectare-învatare prin parcurgerea careia elevul asimileaza continutul ideatic sistematizat în obiectele de studiu , îsi formeaza sistemul de abilitati prevazute de programele scolare.

Diversi specialisti români s-au ocupat de acest concept de strategie educationala ,aducând contributii la definirea sa . Astfel la Cerghit Ioan (4) alegerea strategiei didactice se face sub triplul înteles al cuvântului .

a) ca adaptare a unui mod de abordare a învatarii (prin problematizare, conversatie euristica, algoritmizare etc.);

b) ca optiune pentru un anumit mod de combinare a metodelor, procedeelor, mijloacelor de învatamânt, formelor de organizare a elevilor ;

c) ca mod de programare (selectare , ordonare si ierarhizare) într-o succesiune optima a fazelor si etapelor (evenimentelor) proprii procesului de desfasurare a lectiei, cu specificatia timpului si respectarea unor "principii didactice" .

Cerghit coreleaza strategia cu definirea experientei optime de învatare si demonstreaza implicatiile ei asupra structurii lectiei .

Ţinând seama de capacitatea strategiei de a structura si a modela o situatie de învatare, aceasta se constituie într-o forma specifica si superioara a normativitatii pedagogice .

Din punct de vedere normativ, strategia este mai puternica decât o simpla regulp a unei secvente de învatare ,deci implica un sistem de reguli, pe de alta parte se diferentiaza de rigiditatea unor reguli, algoritm prin flexibilitatea proprie interna .

Actiunile de predare-învatare în cadrul disciplinei matematice la clasele I-IV au determinari concrete, în sensul ca se desfasoara într-un câmp pedagogic definit de o multitudine de variabile a caror interdependenta este logica . Nu se poate vorbi de metode universale, eficiente sau ineficiente, bune sau rele .Fiecare situatie de predare-învasare accepta una sau mai multe variante metodice.

Învatatorul ,cunoscând varietatea metodelor disponibile în câmpul didacticii moderne, cunoscând particularitatile elevilor cu care lucreaza, valentele continutului pe care trebuie sa le atinga prin predare-învatare, trebuie sa actioneze pentru a-si valorifica pe deplin personalitatea, el însusi devenind un autentic subiect în materie de articulare a strategiilor, metodelor si procedeelor didactice.

Continutul matematicii scolare si obiectivele predarii ei centreaza tehnologia didactica pe metoda, componenta cu rol predominant în triada : metoda, mijloace, tehnici .

Prin metoda se întelege acea " cale urmata de învatator împreuna cu elevul, în procesul de învatamânt, în scopul însusirii informatiei de catre elev si a formarii priceperilor si deprinderilor", precizandu-se ca metoda este în principiu proiectata si controlata de învatator .

METODE DE PREDARE- ÎNVĂŢARE

A.De transmitere a cunostintelor

*expozitive: povestirea, descrierea, explicatia, instructajul ;

○ orale

*conversatia :conversatia, discutia colectiva, problematizarea;

*dupa text: lectura, instruirea programata, fisa ,planul de idei, studiul dupa manual ;

○ scrise

*dupa scheme sau alte forme de prezentare .

B.De explorare a realitatii.

○ directe : observatia dirijata, semidirijata si independenta , studiul de caz, experimentul, de descoperire, rezolvare de probleme, exercitiul, jocul explorativ etc.

○ indirecte : descoperirea explorativa, demonstratia experimentala sau substituite, jocurile cu constructia, modelarea .

C.De actiune (mentala sau materiala).

○ reale : exercitiul, algoritmizarea, lucrarea pracica, metode si tehnici creative;

○ simultane : jocul didactic, proiectul didactic, învatarea dramatizata, exercitiul simulat etc.

Specifice predarii-învatarii matematicii la clasele I-IV sunt strategia inductiva si strategia analogica . Ca tip special de abordare a realitatii matematice , în maniera inductiva învatatorul si elevii întreprind experimente asupra situatiei date sau în cadrul ei, efectuând actiuni reale cu obiecte fizice sau cu obiecte create de gândire (concepte). Pe baza observatiilor facute , elevii sunt condusi progresiv la conceptualizari (de exemplu în rezolvari de probleme, prin metoda sinectica, pornind de la datele si relatiile problemei catre întrebarea, elevul gândeste inductiv, dar prin metoda analitica se produce o gândire deductiva, pornindu-se de la întrebarea finala catre datele si relatiile unei probleme ).

Strategia analogica are ca temei o prima si esentiala caracteristica a gândirii matematicii, anume relevanta ei logic-analitica . Vom întâlni analogii între notiuni, între idei, între teoreme, între demonstratii, între domenii . Punctul de plecare îl constituie însusi faptul ca analogia reprezinta forma principala sub care se manifesta procesele de abstractie . Ideea pedagogului canadian Z.P.Dienes care a propus trusa lui devenita celebra în învatamântul matematic, formata din 48 de piese de carton, variabile ca marime (unele mari, altele mici) ca forma (cerc, patrat, dreptunghi, triunghi), ca dimensiune (groase sau subtiri) si culoare (rosu, galben , albastru), reprezinta un model de gândire analogica aritmetico-combinatorie, rezultat al punerii laolalta a obiectelor cu anumite proprietati .

Analiza sintetica a procesului de învatamânt scoate în evidenta legatura logica ce exista între componentele sale : obiective, continut, metode , mijloace, forme de organizare a activitatii, relatii educator-educat, toate vazute în lumina conexiunilor necesare, proiectate si evaluate la parametrii de eficienta ridicata . Orice modificari propuse întruna din aceste componente afecteaza în mod firesc, direct sau indirect, functionalitatea însasi a tuturor celorlalte componente .

În predarea-învatarea matematicii se folosesc urmatoarele metode :

A.1. Metode didactice în care predomina actiunea de comunicare orala expozitiva .

Expunerea asigura prezentarea orala , directa si rapida a cunostintelornoi, într-o organizare logica, fluenta, clara .

Expunerea este înteleasa ca "activitatea învatatorului de a comunica elevilor cunostinte noi, sistematic ,în forma unei prezentari orale închegata si sustinuta", are o pondere relativ redusa în predarea matematicii . Expunerea sub forma de povestire apare când se prezinta unele fapte si date din istoria matematicii fiee ca este vorba de istoria unei probleme a unei descoperiri, fie ca se prezinta viata si opera unui mare matematician . Asemenea povestiri trebuie sa fie scurte, sa faca referiri nimai la aspecte matematice cunoscute elevilor, sa fie metaforice sa induca elevilor o stare emotionala placuta si instructiva .

Explicatia este folosita pentru formarea notiunilor, lamurirea si clasificarea lor, dar si a unor principii, de legi, apelând la diverse procedee : inductie, deductie, comparatie, analogie, analiza cauzala etc.

Explicatiile survin când se introduc termeni matematici noi, când se prezinta o actiune, când se elaboreaza si fixeaza o schema generala de rezolvare a unei probleme .

A.2. Metode didactice în care predomina actiunea de comunicare orala interogativa .

Conversatia se bazeaza pe întrebari si raspunsuri pe verticala, între învatator si elevi, si pe orizontala între elevi . Prepozitia interogativa se afla la granita dintre cunoastere si necunoastere, dintre certitudine si incertitudine . De aceea ,aceasta functioneaza activ în orice situasie de învatare, îmbracând, din acest punct de vedere mai multe forme : conversatia introductiva, folosita ca mijloc de pregatire a elevilor pentru începerea unei activitati didactice, conversatia folosita ca mijloc de aprofundare a cunostintelor, toate acestea având caracteristicile conversatiei catehice .

Conversatia catehica (examinatoare) vizeaza simpla reproducere a cunostintelor asimilate în etapele anterioare, rolul ei de baza fiind cel de examinare a elevilor . Întrebarile si raspunsurile nu se mai constituie în lanturi de serii, ci fiecare întrebare constituie un întreg de sine statator, care poate avea sau nu legatura cu întrebarea care urmeaza .Conversatia examinatoare nu se limiteaza doar la " constatarea nivelului la care se afla cunostintele elevului la un moment dat" . Întrebari specifice conversatiei catehice apar si în reactualizarea continuturilor (Cum se numesc numerele care se aduna ? Dar rezultatul adunarii ?), în etapa discutiilor pregatitoare, pe parcursul transmiterii noilor continuturi, în momentul ce vizeaza intensificarea retentiei si transferului (Ce înseamna faptul ca adunarea este asociativa ?) , pentru fixare, consolidare si aplicare (Ce proprietati are adunarea? ) .

Pentru redescoperirea unor cunostinte se foloseste conversatia euristica , care sporeste caracterul formativ al învatarii , dezvoltând spiritul de observare , capacitatea de analiza si de sinteza, interesul cognitiv si motivatia intrinseca, mobilizând energiile creatoare pentru rezolvarea de probleme si situatii problematice . E vorba despre un sir de întrebari care orienteaza, în mod unidirectional, spre un raspuns pe care învatatorul îl presupune si îl asteapta în toate detaliile lui . Întrebarile acestuia dirijeaza în permanenta gândirea elevilor prin felul si ordinea în care sunt formulate, astfel ca "din aproape în aproape" sa ajunga la finalitatea preconizata . Seria de întrebari este compacta, fiecare noua întrebare depinzândde raspunsul obtinut la întrebare precedenta .

În matematica scolara, aplicarea teoriei în rpactica, trecerea de la general la particular au o importanta mult mai mare decât la alte obiecte de învatamânt .

Conversatia euristica (socratica) consta într-o înlantuire de întrebari si raspunsuri prin intermediul caruia elevii sunt dirijati sa valorifice experienta cognitiva de care dispun si sa faca asociatii care sa faciliteze dezvaluirea de aspecte noi . Printr-un demers inductiv, elevii sunt orientati/dirijati catre relatii cauzale , formularea unor concluzii, desprinderea unor reguli, elaborarea unei definitii etc.

Este folosita mai ales în analiza sau în explicarea metodei de lucru în rezolvarea unei probleme matematice. De exemplu, la tema "Adunarea si scaderea numerelor naturale în concentrul 0-30", analza problemei : "Într-un autobuz erau 29 calatori. La prima statie au coborât 7 .La a doua statie au urcat 14. Câti calatori sunt acum în autobuz ?" se realizeaza astfel :

Î₁ : Câti calatori erau la început în autobuz ?

R₁ : ....29 calatori .

Î₂ : ce sa întîmplat la prima statie ?

R₂ . ....au coborât 7 calatori .

Î₃: Asta înseamna ca în autobuz vor ramâne mai multi sau mai putini calatori ?

R_3
:....mai putini .

Î ₄ . Prin ce operatie vom afla câti calatori ramân în autobuz dupa ce au coborât 7 ?

R ₄ : prin scadere .

Î _5
:Cun ?

R ₅ : Din numarul calatorilor care erau la început scadem numarul calatorilor care au coborât : 29 - 7 = 22.

Î ₆ : Ce sa întâmplat la a doua statie ?

R ₆ : ... au urcat 14 calatori .

Î ₇ : Asta înseamna ca în autobuz vor fi mai multi sau mai putini calatori ?

R ₇: ...mai multi .

Î ₈ Prin ce operatie vom afla câti calatori sunt dupa ce au urca 14 ?

R ₈: ... prin adunare : numarul calatorilor care erau în autobuz îl adunam cu numarul calatorilor care s-au urcat , 22 + 14 = 36 .

Conversatia poate fi folosita în predarea noilor cunostinte, în verificarea cunostintelor asimilate, în pregatire lectiei noi, în sistematizarea lectiei si fixarea cunostintelor predate, în activitatea de rezolvare a problemelore. Aceasta poate avea caracter individual , îndeosebi când se foloseste în verificare , sau frontal, atunci când se antreneaza toata clasa la elaborarea raspunsurilor .

Instrumentul de lucru al metodei-întrebare trebuie stapânit si perfectionat continuu de fiecare învatator . Întrebarile adresate memoriei, daca nu pot fi evitate , trebuie completate de întrebari care solicita gândirea si care pot lamuri calitatea raspunsului respectiv .La matematica trebuie sa predomine întrebarile care încep prin "de ce ? "cu rol de incitare la gândirea productiva .

Întrebarile trebuie sa fie exprimate concis, simplu si clar .

Conversatia consta din " valorificarea didactica a întrebarilor si raspunsurilor" prin care se stimuleaza si dirijeaza activitatea de învatare a elevilor .

În literatura de specialitate sunt prezentate mai multe tipuri de conversatie :

● conversatia de fixare si consolidare , utilizata pe parcursul transmiterii noilor continuturi, în etapa ce vizeaza intensificarea retentiei si transferului de cunostinte ; (Daca un numar este de 4 ori mai mare decât 5 , prin ce operatie îl vom afla ? Dar daca este cu 4 mai mare decât 5 , cum îl vom calcula?) ;

● conversatia de reactualizare si sistemizare , folosita în special îl lectiile de recapitulare si sistematizare sau în momentele de reactualizare a cunostintelor-ancora pentru a-i pregati pe elevi în asimilarea noilor informatii ( Ce proprietati are operatia de înmultire ?);

● conversatia de verificare (convergenta-divergenta), utilizata pe parcursul transmiterii noilor informatii , în momentele de verificare a gradului de întelegere a cunostintelor de catre elevi (De ce spunem ca înmultirea este comutativa ) ;

● conversatia introductiva, folosita în etapa discutiilor pregatitoare pentru a capta atentia si amplifica interesul si motivatia elevilor (Ce este un patrulater ?Ce patrulatere cunoasteti ? ) ;

● conversatia finala , la sfârsitul unei secvente de învatare cu scopul realizarii feedback-ului sau verificarii nivelului de însusire a continuturilor (Într-un exercitiu cu adunari, scaderi, înmultiri si împartiri în ce ordine rezolvam operatiile ? ) ;

● conversatia de comunicare, utila în partea de încheiere a unei experiente de rezolvare a unei probleme sau în pararel cu aceasta, în comentarea exemplelor concrete ori complementarea materialului didactic, pentru dirijarea observatiei elevilor si sublinirea aspectelor esentiale etc.

Eficienta utilizarii oricarei forme de conversatie didactica este conditionata de alegerea momentului de utilizare a metodei în lectie, de ponderea folosirii sale, dar si de calitatile întrebarilor, pe de o parte , si a raspunsurilor pe de alta parte .

Metoda conversatiei are o mare valoare formativa si datorita introducerii si exersarii limbajului specializat al matematicii , contribuie la dezvoltarea personalitatii elevilor .

Brainstormingul (metoda asaltului de idei) presupune o organizare specifica a timpului, desfasurat pe doua etape distincte : etapa producerii individuale a ideilor, pe baza problemei lansate de cadrul didactic si de etapa aprecierii finale a ideilor , sustinuta critic de cadrul didactic aflat în ipostaza de conducator al activitatii . Are loc asadar, o "evaluare amânata" strategic, pentru activizarea tuturor elevilor, emiterea si consemnarea a cât mai multor idei .

Problematizarea urmareste realizarea activitatii de predare-învatare-evaluare prin lansarea si rezolvarea unei situatii-problema , care " desemneaza o situatie contradictorie, conflictuala, ce rezulta din trairea simultana a doua realitati ( de ordin cognitiv si motivational ) incompatibile între ele pe de o parte experienta trecuta, iar pe de alta parte elementul de noutate si de surpriza , necunoscutul, cu care este confruntat " elevul .

Metoda problematizarii se mai numeste si predarea prin rezolvarea productiva de probleme . Problematizarea se mai defineste si ca o metoda didactica ce consta în punerea în fata elevului a unor dificultati create în mod obiectiv, prin depasirea carora, prin efort propriu, elevul învata ceva nou . Dificultatile vizate de metoda pot fi într-o gama variata , dar esenta lor consta în "crearea unor situatii conflictuale în mintea elevului " numite si situatii problematice .

Specificul metodei este dat de notiunea de situatie-problema care reprezinta o stare "vaga" conflictuala care se recreaza în mintea elevului din trairea simultana a doua realitati : experienta anterioara (cognitiva-emotionala) si elementul de noutate si de surpriza cu care se confrunta subiectul .

Principalele situatii-problema pot fi :

1. când exista un dezacord între vechile cunostinte ale elevului si cerintele impuse de rezolvarea unei probleme ;

2. când elevul trebuie sa aleaga dintr-un lant sau sistem de cunostinte, chiar incomplete, numai pe cele necesare în rezolvarea situatiei date ;

3. cînd elevul este pus în fata unei contradictii între modul de rezolvare posibil din punct teoretic si imposibilitatea aplicarii lui în practica ;

4. când elevul este solicitat sa sesizeze dinamica miscarii chiar într-o schema aparent statica ;

5. cînd elevului i se cere sa aplice în conditii noi cunostintele asimilate anterior .

Aplicarea acestei metode presupune o serie de conditii care nu pot fi ignorate :

● toti elevii sa fie obisnuiti a fi activi la lectiile de matematica ;

● elevii sa fie obisnuiti a lucra individual în timpul orei sau în colaborare în grupe mici ;

● sa fie folosita metoda descoperiri de mai multe ori ;

● majoritatea elevilor sa fie buni rezolvatori de probleme , sa manifeste si sa fie lasati sa-si manifeste creativitatea ;

● elevii sa fie obisnuiti cu atitudinea de colaborator apropiat pe care învatatorul trebuie sa o aiba în folosirea aceste metode ;

● sa existe în colectivul de elevi un spirit de întrecere si cei talentati sa fie apreciati corespunzator de colegi ;

● sa fie obisnuiti a gândi nota ca reconpensa pe plan secund, satisfactia principala fiind întelegerea, descoperirea, creatia .

În cazul problematizarii, cunostintele nu mai sunt prezentate în forma lor initiala . Ele sunt interpretate, reasezate , chiar rasturnate epistemic, pentru a putea genera o noua solutie. Propunerea problematizarii ca si cale de învatare în cadrul didacticii matematicii presupune respectarea a doua conditii .

1. exersarea si stapânirea deplina a cunostintelor pentru ca astfel rasturnarea lor poate genera esec scolar ;

2. stimularea creativitatii superioare, nu orice creativitate .

Neacsu Ioan (24) ordoneaza situatiile problematice pe cinci categorii :

1. când exista un dezacord între vechile cunostinte ale elevului si cerintele impuse de rezolvarea unei probleme ;

2. când elevul trebuie sa aleaga dintr-un lant sau sistem de cunostinte, chiar incomplete, numai pe cele necesare în rezolvarea situatiei date ;

3. cînd elevul este pus în fata unei contradictii între modul de rezolvare posibil din punct teoretic si imposibilitatea aplicarii lui în practica ;

4. când elevul este solicitat sa sesizeze dinamica miscarii chiar într-o schema aparent statica ;

5. cînd elevului i se cere sa aplice în conditii noi cunostintele asimilate anterior .

Un exemplu de situatie-problema îl putem întâlni în predarea ordinii operatiilor .Anterior acestei lectii elevii au rezolvat exercitii în care apar doar operatii de ordinul I, adunari si scaderi . Putem crea urmatoarea situatie-problema :

Care este rezultatul corect ?

2 + 3 x 5 - 7 = 18 sau 10

Pe baza experientei si a cunostintelor pe care le au , elevii vor rezolva operatiile în mod incorect, în ordinea în care apar :

2 + 3 x 5 - 7 = 25 - 7 = 18

Pentru a iesi din aceasta dilema propunem elevilor spre rezolvare urmatoarea problema : Ionut are 2 caramele , primeste de la fiecare din cie 3 prieteni ai sai câte 5 caramele si-i da fratelui sau 7. Câte caramele are acum Ionut ?

Scrierea rezolvarii acestei probleme sub forma de exercitiu îi conduce catre rezultatul corect .Se observa din planul de rezolvare al problemei ca operatia de înmultire se efectueaza înaintea adunarii . Se generalizeaza acest lucru si se extrage regula ordinii efectuarii operatiilor .

În problemele în care întâlnim distributivitatea înmultirii fata de adunare, obtinem doua rezolvari .

Exemplu : Într-o livada sunt 6 rânduri a câte 10 meri si 3 rânduri a câte 10 pruni . Câti pomi sunt în livada ?

Astfel putem calcula pe rând numarul merilor si numarul prunilor, iar în final adunam produsele obtinute ; sau calculam câte rânduri de pomi sunt în livada si suma o înmultim cu 10 .

Se constata ca : 6 x 10 + 3 x 10 = ( 6 + 3) x 10

Antrenând toate componentele personalitatii (intelectuale, afective, volitive) problematitarea contribuie la stimularea interesului, curiozitatii, spiritului de exploatare al elevilor .Elevii îsi formeaza treptat un stil individual de munca, îsi dezvolta independenta în gândire, autonomia, curajul în argumentarea si sustinerea solutiilor proprii de rezolvare .

Descoperirea poate fi definita "ca o tehnica de lucru, la care elevul este antrenat si se angajeaza în activitatea didactica, cu scopul aflarii acevarului ". Prin aceasta metoda elevii, redescopera relatii, formule, algoritmi de calcul.

Aceasta atitudine a elevului nu poate subzista decât pe o pregatire anterioara solida, o exersare ce a creat deprinderi corespunzatoare. Mai mult, întreaga activitate de (re)descoperire este dirijata de profesor, astfel ca problema centrala ridicata de metoda este unde si cât sa-l ajute învatatorul pe elev .

Eficienta metodei depinde esential de raspunsul corect la aceasta întrebare . Aceasta cere învatatorului tact pedagogic si o cunoastere a problemei în toate articulatiile ei, inclusiv în locul în care elevii pot întâmpina greutati . Tactica folosita de învatator este aceea de a plasa sugestii "usoare" în momentele de dezorientare ale elevilor, momente ce pot fi citite pe fetele lor .

În descoperirea de tip deductiv elevii pot obtine rezultate noi (pentru ei) aplicând ratioanmente asupra cunostintelor anterioare, combinându-le între ele sau cu noi informatii. Acest tip de descoperire apare frecvent la : de exemplu cunoscând aria patratului descoperim aria triunghiului, apoi aria paralelogramului, a triunghiului, a rombului ,a trapezului.

Formulele de calcul prescurtat pot fi descoperite cu mare usurinta în acest mod . Algoritmii de calcul mintal prin aplicarea proprietatilor operatiilor cu numere naturale pot fi descoperiti deductiv .

Descoperirea prin analogie consta în transpunerea unor relatii, algoritmi etc., la contexte diferite, dar analoage într-un sens bine precizat . Algoritmii de rezolvare a problemelor de un anumit tip pot fi un exemplu de descoperire prin analogie . Analogiile în matematica pot fi de continut sau de rationament . Ele pot fi de anvergura mai mare sau cu efect local .Analogii mari folosite în matematica sunt cele din aritmetica si algebra , geometrie plana si geometrie în spatiu .

Analogia de rationament poate fi folosita în rezolvarea problemelor, în predarea multiplilor si submultiplilor unitatilor de masura , în demonstrarea formulelor pentr perimetru sau arii .

A.3.Metode didactice în care predomina actiunea de comunicare scrisa , valorifica lectura în acceptia acesteia de "tehnica fundamentala de munca intelectuala ".

Activitatea cu manualul si alte carti (culegeri de matematica) constituie o forma a lucrului independent . Aceasta metoda se aplica atât în timpul orelor de matematica, cât si acasa, pentru rezolvarea temelor. Descifrarea sensului matematic este primordial pentru rezolvarea cerintelor, care pot fi mai putin explicite si atunci elevul trebuie sa complteze detaliile lipsa .

Aceasta metoda este strâns împletita cu metoda descoperirii si a problematizarii încât deseori ne apare ca un procedeu . Manualele , culegerile de probleme si alte carti noi , cunostinte, sa le sistematizeze si fixeze sa-si formeze priceperi si deprinderi si de aceea în matematica ea se poate impune ca o metoda .

Elevii trebuie sa învete cum sa foloseasca manualele si alte carti pentru a sti cum sa le utilizeze ulterior pentru perfectionarea continua . Manualul trebuie folosit atât pentru exercitii cât si pentru aplicatii, pentru documentare, pentru evaluare, pentru munca independenta .

Lucrând cu manualul, elevul este activ, obtinând cunostintele printr-un efort propriu astfel încât aceasta metoda devine "o cale de instruire prin decoperire ".

Nu este bine sa facem abuz de aceasta metoda si nici sa o folosim limitându-ne la indicatia "cititi lectia din carte" fara a finaliza ofixare a cunostintelor si o verificare a modului de însusire a lor.

În folosirea metodei aspectul formativ cel mai important este formarea deprinderilor de a studia dupa manual, mai general dupa carti . Acest aspect trebuie urmarit si prin mijloace directe .Astfel învatatorul va explica elevului cum se citeste un text de matematica .Etapele obisnuite în descrierea unui text matematic sunt :

● citirea lui în întregime pentru asesiza ideea sau ideile generale si împartire lui în unitati logice ;

● analiza textului începând cu definitiile si continuând cu enunturile exercitiilor si problemelor .

O sistematizare a temei se poate face prin .

● studiul rezolvarilor unor exercitii si probleme;

● efectuarea de exercitii apicative cu rol de fixare precum si aprofundare a unor aspecte ;

● consemnarea schemei sintetizatoare în caietu elevilor lânga exercitiile efectuate .

Este foarte important de amintit elevilor ca studiul unui text se face cu creionul în mâna si ca rezolvarile si demonstratiile se refac în toate detaliile .

B.1.Metode didactice în care predomina actiunea de cercetare directa a realitatii .

Observatia este o activitate perceptiva, intentionata, orientata spre un scop, reglata prin cunostinte, organizata si condusa sistematic, constient si voluntar . Aceasta metoda asigura baza intuitiva a cunoasterii, permite o perceptie polimodala , asigura formarea de reprezentari clare despre obiecte devenite material didactic si însusirilecaracteristice ale acestora, asigura investigarea directa a unor relatii , corelatii . Ca metoda , observatia este însotita de explicatie-elementul de dirijare a observatiei . Trebuie permanent avut în vedere utilizarea unui limbaj care însoteste observatia . Perfectionarea metodei vizeaza asigurarea saltului de la observatia sistematica dirijata, la observatia sistematica realizata independent de elev .

B.2.Metode didactice în care domina actiunea de cercetare indirecta a realitatii .

Demonstratia presupune prezentarea unor obiecte , procese, fenomene reale sau substituite, cotact prin care se obtine reflectarea obiectului învatarii la nivelul perceptiei si reprezentarii . La baza demonstratiei se afla întotdeauna un mijloc de învatamânt, de aici si tendinta definirii acestei metode drept "metoda intuitiva" .

Este utilizata în mai multe forme :demonstratie observationala numita si "demonstratie vie" bazata pe prezentarea unor obiecte reale, în stare naturala (folosirea "metrului de tâmplarie" pentru a demonstra ca 1m = 100 cm etc.) ; demonstratia cu actiuni (demonstrarea la tabla a modului de utilizare a instrumentelor pentru a trasa 2 drepte paralele ) ; demonstratia figurativa , cu ajutorul materialului confectionat (compunarea de probleme la clasa I) ;demonstratia grafica, pe baza de tabele, scheme grafice (rezolvarea problemelor prin metoda grafica ) ; demonstratia logica de stabilire a adevarurilor prin rationament (distributivitatea înmultirii fata de adunare ) ; demonstratia prin exemple, rezolvând exercitii si probleme asemanatoare, prin acelasi procedeu ; demonstratia cu ajutorul modelelor ideale (formule, scheme grafice ) .

Metoda demonstratie intuitive este intens folosita în clasele învatamântului primar, iar la clasele mai mari, demonstratia matematica se bazeaza pe modele, structuri, scheme matematice. Se pot aminti urmatoarele conditii necesare pentru eficientizarea demonstratiei :

● constientizarea scopului urmarit ;

● reactualizarea cunostintelor esentiale ;

● prezentarea sarcinii într-o forma dinamica cu sprijinul mijloacelor de învatamânt ;

● asigurarea unui ritm corespunzator al demonstratiei pentru a da posibilitatea elevilor sa realizeze însusirea corecta a structurilor propuse ;

● activizarea întregii clase în timpul demonstratiei si ulterior acesteia în etapa prelucrarii datelor obtinute pe aceasta cale .

Metoda prezentarii materialului didactic este expresia demonstratiei intuitive si a respectarii principiului intuitiei în procesul de predare-învatare a matematicii . Aceasta metoda se foloseste cu preponderenta la prescolarii si scolarii din ciclul primar, când intuitia predomina .

Demonstratia ca metoda intuitiva, este dominata în activitatile de dobândire de noi cunostinte .Metoda , fara a fi folosita exagerat, are efect favorabil asupra întelegerii si retinerii cunostintelor si dezvolta capacitatea de a observa ordonat, sistematic si de a exprima coerent datele problemei .

Modelare este o "constructie substantiala sau mintala a unor modele materiale sa mintale analogice ale realitatii, folosite ca instrumente în organizarea învatarii" . Modelul "este un rezultat al acestei constructii artificiale bazate pe rationamente de analogie , pe un efort de gândire deductiva ".

Matematica valorifica modelarea si modelul în sensul simplificarii, schematizarii, esentializarii, aproximarii realitatii . De aceea trebuie cunoscute oferte de diferite tipuri de modele si modelare :

● modelare prin similitudini :

● modelare prin analogie ;

● modelare simbolica (tipic matematica) ; acest model este o "abstractie " care pune în evidenta fenomenul sau procesul sub o forma pura ; exprima un raport, o legitate, printr-o simpla formula : P = (L -l) ; A = L x l etc. Cu posibilitatea de aplicare în calcule , în practica, în rezolvarea de probleme .

Modelarea reprezinta forma cea mai riguroasa analogiei prin transcriere simbolica matematica a unui mod de desfasurare a unei structuri, alcatuirea unui sistem .

C.1. Metode în care predomina actiunea didactica practica operationala reala .

Exercitiul este o metoda ce are la baza actiuni motrice si intelectuale, efectuate în mod constient si repetat, în scopul formarii de priceperi si deprinderi, automatizarii si interiorizarii unor modalitati sau tehnici de lucru, de natura motrica sau mintala . Ansamblul deprinderilor si priceperilor dobandite si exersate prin exercitii în cadrul orelor de matematica conduc la automatizarea si interiorizarea lor, transformându-se treptat în abilitati . Fiecare abilitate se dobândeste prin conceperea , organizarea, rezolvarea unui sistem de exercitii .

În cadrul orelor de matematica se pot rezolva mai multe tipuri de exercitii :

● dupa functia îndeplinita : introductive, de baza, operatorii ;

● dupa modul de rezolvare: de calcul oral, de calcul mintal, scrise, de calcul în scris ;

● dupa gradul de interventie al învatatorului : dirijate. semidirijate, libere;

● dupa subiectii care le rezolva : individuale (rezolvate prin munca independenta), în echipa, frontale ;

● dupa obiectivul urmarit : de calcul, de completare, de ordonare ,de comparare, de comunicare, de rezolvare a problemelor, de formare a deprinderilor intelectuale , de creativitate, de autocontrol etc.

Exercitiul face parte din categoria metodelor algoritmice deoarece presupune respectarea riguroasa a unor prescriptii si conduce spre o finalitate stabilita .Nu orice actiune pe care o executa elevii constituie un exercitiu , ci numai aceea care se repeta relativ identic si se încheie cu formarea unor componente automatizate ale activitatii .

Exercitiile constituie un instrument extrem de util în fixarea si retinerea cunostintelor, de aceea, metoda exercitiului se combina cu metode active de predare . Dupa introducerea unor notiuni noi, a unor procedee noi, primele exercitii ce se propun sunt exercitii descrise de învatator, fie (re)descoperite de ei cu ajutorul învatatorului .

De exemplu : când dorim sa efectuam proba împartirii cu rest se explica regula a = bx c + r , se repeta cu elevii regula prin exemple concrete.

Dupa întelegerea regulii, a operatiilor, elevii o repeta de câteva ori pentru formarea deprinderii de a o folosi . Aceste exercitii se numesc exercitii de baza .

Dupa introducerea unei noi notiuni si derularea exercitiilor de antrenament si a celor de baza sunt necesare exercitii în care sa se urmareasca si întarirea deprinderilor anterioare odata cu deprinderile noi, integrarea acestor doua categorii de deprinderi . Asemenea exercitii se numesc exercitii paralele sau analoage .

Cantitatea si durata exercitiilor trebuie sa asigure formarea de priceperi si deprinderi ferme . Pentru predarea notiunii de fractie se trece de la exercitii practice de antrenament, la exercitii de baza de scriere si recunoastere a fractiei si prin exercitii paralele de comparare a fractiilor si de recunoastere a apartenentei într-o clasa echivalenta .

Rolul învatatorului este de a propune exercitiile, de a urmari corectitudinea rezolvarii, de a analiza cu elevii eventualele greseli si cauzele lor, de a interpreta rezultatele exercitiilor si de a aprecia calitatea deprinderilor de rezolvare ale elevilor .

Metoda exercitiului, este necesara în diirjarea cel putin în faza de început , dar si pe parcurs, când sunt necesare corectari, restructurari . De altfel, exercitiul este o metoda necesara ori de câte ori avem ca obiectiv formare, dezvoltarea unei deprinderi a matematicii (intelectuale, psihomotorii) . În acelasi timp , exercitiul în diferite forme, variate, trebuie sa fie un procedeu subordonat metodei demonstratiei, descoperirii, modelarii sau problematizarii . El este un punct de sprijin intuitiv si formativ, dar si o solutie alternativa aplicata atunci când metoda da roade . Exercitiul preconizat ca procedeu pe o anumita perioada de timp a lectiei devine metoda , cale de învatare, valabila pe tot parcursul lectiei .

Literatura de specialitate propune diverse clasificari ale exercitiilor, în functie de criteriile adoptate .

Dupa forma lor exercitiile pot fi :

● orale ( numarati din 3 în 3 începând cu 0 ; citeste numerele: 724321, 543076, 890098; care sunt vecinii numerelor );

● scrise ( calculati, apoi faceti proba prin operatia inversa : 344+543; 765-654; descompuneti numerele în sute, zeci si unitati : 543, 657 , 666 ; efectuati calculele si compltati tabelul ....; aflati termenul necunoscut : x+543 = , = 876 ,y-240=375);

●practice ( masurati lungimea bancii cu palma ; câte pahare pot umple cu apa din acest bidon ? ; construieste patrate, dreptunghiuri si triunghiuri din betisoare, creioane sau bete de chibrit ...) .

Dupa functia îndeplinita ,exercitiile se clasifica în :

● exercitii introductive (exercitii de calcul mintal de la începutul orei de matematica; exercitii de adunare repetata care pregatesc întelegerea operatiei de înmultire ) ;

● exercitii de baza ( de însusire a modelului dat );

Exemple : 1) Scaderea cu trecere peste ordin ( efectuati prin calcul scris) :

2) Împartirea cu rest ( calculati câtul si restul 26 : 4 = , 38 : 5 =)

3) Ordinea efectuarii operatiilor (calculati 2 x 7 x 3 - 8 : 2 - 10 = )

● exercitii paralele de legare acunostintelor si deprinderilor mai vechi cu cele mai noi ;

Exemple : 1) Împartirea numerelor naturale de trei cifre la un numar scris cu o cifra ( calculati apoi faceti proba : 324 :3 = , 728 : 4 = ) ;

2) Ordinea efectuarii operatiilor si folosirea parantezei ( efectuati : 30 - = ; aflati valoarea lui X : 2 x = ) ;

● exercitii de creatie ( euristice)

Exemple : 1) compune exercitii de adunare si de scadere cu trecere peste ordin, folosind numere mai mici de 50 ;

2) compune câte o problema care sa se rezolve prin : doua adunari , o adunare si o scadere, o înmultire si o adunare ;

Dupa continutul lor , pot fi doua categorii :

● exercitii motrice , care conduc spre formarea de deprinderi în care predominanta este componenta motrica ( exemplu : scrieti 3 rânduri cu cifra 8)

● exercitii operationale care contribuie la formare operatiilor intelectuale, principale lor trasaturi fiind reversibilitatea si asociativitatea .

Exemple : 1) Perimetru patratului ( calculeaza perimetrul unui patrat cu latura de 5 cm ; calculeaza latura unui patrat cu perimetrul de 20 cm ) ;

2) Perimetrul dreptunghiului (calculeaza perimetrul unui dreptunghi cu lungimea de 6 cm si latimea de 7 cm ) .

Dupa numarul de participanti pot fi :

● exercitii individuale ;

● exercitii de echipa ;

● exercitii colective ;

● exercitii mixte.

Dupa gradul de complexitatea se diferentiaza :

● exercitii simple 3 + 5 =

● exercitii complexe X : 3 = 7 rest 4

● exercitii super-complexe (tip olimpiada ) 257 : = 8 rest 1

Algoritmizarea angajeaza un lant de exercitii, operatii dirijate, executate într-o anumita ordine, aproximativ constanta, integrate la nivelul unei scheme de actiune didactica standardizata ajungându-se în acestfel la o înlantuire logica de continuturi, în vederea îndeplinirii sarcinilor de instruire .

Activitatea de învatare este efiencietizata prin calitatea corespunzatoare a algoritmilor alesi de a interveni ca modele operationale . Metoda ofera elevului un instrument simplu si operativ, scutindu-l de cautari . Prin structura precisa a algoritmilor, prin mânuirea lor repetata, elevul reuseste sa-si "disciplineze propria gândire ".

Algoritmizarea este cunoscuta ca "metoda de predare-învatare constând din utilizarea si valorificarea algoritmilor" .

Algoritmii se prezinta sub diferite forme : reguli de calcul, scheme de rezolvare a unei probleme, scheme operationale etc. Algoritmizarea reprezinta o metoda care tine de dimensiunea "mecanica" a învatarii, asa cum precizeaza C. Cucos (11) , eficienta ei constând în faptul ca ofera elevului un instrument de lucru operativ, economicos, scutindu-l de cautari, iar prin mânuirea repetata a algoritmilor, elevul reuseste sa-si "disciplineze" propria gândire .

Jocul didactic, cametoda , cunoaste o larga aplicabilitate regasindu-se în cadrul tuturor orelor de matematica . Metoda jocului didactic reprezinta o actiune care "valorifica nivelul instructiei , finalitatile adaptive de tip recreativ proprii activitatii umane, în general, în anumite momente ale evolutiei sale ontogenice, în mod special" .

Restabilind un echilibru în activitatea scolarului, jocul fortifica energiile intelectuale si fizice ale acestuia, generând o motivatie secundara, dar stimulatoare, constituind o prezenta indispensabila în ritmul accentuat al muncii scolare .

Prin intermediul motivatiilor ludice care sunt subordonate scopului activitatii de predare-învatare-evaluare învatatorul dinamizeaza actiunea didactica într-o perspectiva pronuntat formativa . Astfel , prin utilizarea jocului ca metoda , se accentueaza rolul formativ al activitatilor matematice:

● exersarea operatiilor gândirii (analiza, sinteza, comparatia, generalizarea, abstractizarea ) ;

● dezvoltarea spiritului de observatie ;

● dezvoltarea imaginatiei si creativitatii elevilor ;

● dezvoltarea spiritului de initiativa, de independenta dar si de echipa ;

● formarea unor deprinderi de lucru corect si rapid, deprinderi de munca independenta ;

● însusirea constienta într-o forma accesibila, temeinica,placuta si rapida a cunostintelor matematice ;

● activizarea copiilor din punct de vedere cognitiv, actional si afectiv, sporind gradul de întelegere si participare activa a copilului în actul de învatare;

● ofrmarea autocontrolului eficient al conduitei si achizitiilor.

În cadrul orelor de matematica se pot folosi ( dupa Ioan Cerghit si Ioan Necsu (5) ):

● dupa forma de exprimare : jocurile simbolice, jocurile conceptuale, jocurile ghicitori ;

● dupa resursele folosite : jocurile materiale, jocurile orale , jocurile pe baza de întrebari, jocurile pe baza de fise individuale, jocuri pe calculator ;

● dupa regulile instituite : jocuri cu reguli transmise prin traditie, jocuri cu reguli inventate, jocuri spontane ;

● dupa competentele psihologice stimulate : jocuri de observatie, jocuri de atentie, jocuri de memorie, jocuri de gândire, jocuri de imaginatie .

În general, un exercitiu sau o problema matematica poate deveni joc didactic daca îndelpineste urmatoarele conditii :

● realizeaza un obiectiv sau o sarcina din punct de vedere matematic ;

● foloseste elemente de joc-întrecere individuala sau pe grupe de elevi, cooperarea între participanti, reconpensarea rezultatelor bune sau penalizarea greselilor comise, aplauze, surpriza, asteptarea, cuvântul stimulator etc. În vederea sarcinilor propuse ;

● foloseste un continut matematic accesibil, atractiv si recreativ prin forma de desfasurare, prin materialul didactic ilustrativ utilizat, prin volumul de cunostinte la care se apeleaza ;

● foloseste reguli de joc cunoscute anticipat de elevi, respectate de acestia , în vederea realizarii sarcinii propuse si a stabilirii rezultatelor .

D. Metode didactice în care predomina actiunea de programare speciala a instruirii .

Metoda instruirii programate

Metoda instruirii programate organizeaza actiunea didactica, aplicând principiile ciberneticii la nivelul activitatii de predare-învatare-evaluare, conceputa ca "un sistem dinamic, complex, constituit dintr-un ansamblu de elemente si de interrelatii".

Dupa modul în care se asigura algoritmul de instruire se delimiteaza mai multe tipuri de programare :

Programarea liniara - are urmatoarea structura de proiectare a secventelor de instruire : informarea elevului, prezentarea sarcinii didactice (întrebare, exercitiu, problema) ,rexolvarea spatiului si a timpului necesar pentru îndeplinirea sarcinii si oferirea variantei corecte de raspuns .

Programarea ramificata - solicita un efort intelectual mai mare din partea elevului pentru recunoasterea raspunsului corect din mai multe raspunsuri date (trei, patru). Daca nu reuseste de la prima încercare, primeste o informatie suplimentara, dupa care trebuie din nuo sa aleaga raspunsul corect, astfel încât sa poata trece la pasul urmator . Structura de organizare a instruirii ramificate se prezinta astfel : informarea elevului, prezentarea sarcinii didactice, rezervarea spatiului si a timpului pentru alegerea raspunsului, întarirea pozitiva în cazul raspunsului corect si trecerea la secventa urmatoare sau întarirea negativa în cazul unui raspuns incorect, care orienteaza elevul spre a informa, care orienteaza elevul spre a informatii suplimentare, obligatorie pentru corectarea raspunsului . Greseala este folosita în acest caz ca mijloc de stimulare a elevului în vederea autocorectarii.

Programarea combinata - realizeaza îmbinarea celor doua tipuri principale , folosind concomitent atât secvente cu raspunsuri construite , cât si secvente cu raspunsuri la alegere .

Programarea elaborata se pune la dispozitia fiecarui elev, utilizând : manuale programate sau fise programate (cu un continut mai redus, al lectiei sau al unui moment al lectiei) si masini de instruire, cu ajutorul carora se administreaza programul elaborat . Calculatorul asigura realizarea instruirii programate în conditii optime . Aceasta metoda poate fi folosita în cadrul orelor de matematica cu mai multa usurinta decât în altele, ca urmare a organizarii logice stricte a continutului . Atfel , programul creat trebuie sa prevada toate punctele în acre elevul ar putea sa gaseasca si apoi sa prevada continuari, care sa-l ajute sa elimine eroarea, în acest fel elevul îsi autoregleaza constient procesul de asimilare .

Îmbinarea instruirii programate cu alte metode si mijloace curente si forme de organizare constituie o modalitate eficienta de însusire si consolidare a cunostintelor. Învatatorul, cunoscând varietatea metodelor disponibile în câmpul didacticii moderne, cunoscând particularitatile elevilor cu care lucreaza, valentele continutului pe care trebui sa le atinga prin predare-învatare, sa actioneze pentru a valorifica pe deplin personalitatea, el însusi devenind un autentic subiect creator în materie de articulare a strategiilor, metodelor si procedeelor didactice .

Instruirea programata numita si " învatamânt prin stimulare", reprezinta "o tehnica moderna de instruire, care propune o solutie noua la problema învatarii". Prin aceasta metoda instruirea se dirijeaza printr-un program pregatit dinainte pe care elevul îl parcurge independent . Programul creat este astfel alcatuit încât elevul sa-si autoregleze constient procesul de asimilare . Asadar, o prima conditie ce trebuie sa o satisfaca un program bun este de a prevedea toate punctele în acre elevul ar putea sa gaseasca si apoi sa prevada continuari care sa-l ajute pe elev as elemine eroarea.

Aceasta conditie este mai lesne de îndeplinit la matematica datorita organizarii logice stricte a continutului .Ea poate fi de asemenea satisfacuta de programele construite din " pasi mici", unitati logice mici usor de asimilat, atât de mici încât elimina posibilile erori . Aceste modele de alcatuire a programului de instruire propus , asigura conditii de succes pentru elev, succes care-l mobilizeaza sa continuie parcurgerea programei . Metoda instruirii programate este o metoda activa pentru ca programa îi cere sa rezolve diferit sarcinile didactice . Din punct de vedere al metodologiei, instruirea programata ridica probleme legate de mijloacele instruirii programate si de organizarea lectiilor .Programele pot fi liniare, ramificate sau combinate . Îmbinarea instruirii programate cu alte metode si mijloace didactice curente si forme de organizare contituie o modalitateeficienta de însusire si consolidare a cunostintelor .

Baza psihologica a utilizarii mijloacelor de învatamânt . Corelatia dintre intuitiv si logic .

Continutul stiintific al conceptelor matematice moderne nu exclude ci dimpotriva, presupune utilizarea unor metode si procedee bazate pe intuitie .

Copilul de vârsta scolara mica are o gândire care opereaza la nivelul operatiilor concrete . Numai în masura în care elevul va fi pus de catre învatator în situatia de a gândi va putea patrunde în întelesul real al conceptalor matematice, îsi va însusi logica acestora. Manifestând initiativa în crearea si folosirea unor metode didactice care sa sprijine întelegerea notiunilor matematice, învatatorul va tine seama de câteva cerinte pentru a oferi posibilitatea elevilor de a învata matematica gândind mai întâi la nivelul concret si pentru a se ridica treptat la întelegerea si operarea cu abstractiunile matematice .

În primul rând, se impune drept cerinta analiza si utilizarea materialelor didactice în functie de gradul lor de intuitivitate, tinând seama de faptul ca interactiunea dintre analogie si inductie, pe de o parte, si temeiul lor intuitiv pe de alta, asigura progresiv evolutia spre abstract .

Materialul didactic principal îl constituie multimile de obiecte cu putere de simbolizare a relatiilor matematice, ale caror elemente dispun de însusiri precise de constituire a multimilor cum sunt : piesele jocurilor logico-matematice , riglete si alte truse din aceasta categorie . Aceste materiale ofera posibilitatea efectuarii unor operatii concrete în care se evidentiaza proprietatea, principiul, relatie ce constituie esenta matematica a conceptelor pe care le învata elevii . Esentializarea se accentueaza cu ajutorul reprezentarilor grafice .

Suportul intuitiv al notiunilor matematice se asigura si prin imagine ale obiectelor constituite în multimi . Acestea însa nu ofera posibilitatea operarii cu ele , de unde si caracterul lor static, constatativ. Folosirea cu precadere si în mod abuziv a unor asemenea mijloace intuitive ascunde esenta matematica, aspectele concrete nedozate îngreunând procesul de esentializare .

Se impune selectionarea atenta a materialelor intuitive în raport de obiectivele urmarite în lectie, în functie de etapa de formare a notiunilor respective, de experienta de care dispun elevii, de masura în care materialul respectiv serveste la întelegerea principiului, a relatiei, a proprietatii etc. Ce urmeaza a fi asimilate , aplicate si apoi transferate .

Se impune dozarea judicioasa a intuitiei , ca suport materia, pâna la nivelul necesar producerii saltului în abstrac, cu retinerea pe plan logic "interiorizare" a adevarului matematic respectiv în limbaj matematic (notiuni) .

Moduri de organizare a activitatilor de matematica .

Organizarea îmvatamântului pe clase si lectii experienta traditionala în vigoare , a instituit un mod apreciat si astazi ca fiind pertinent si eficient în multe situatii, anume modul frontal de lucru cu elevii .

Practica educationala a cunoscut si cunoaste si alte moduri de organizare a procesului instructiv-educativ privit din punctul de vedere al agentilor educationali.

Se are în vedere activitatea de grup (grupuri omogene, grupuri eterogene, grupuri competitive, grupuri cooperante etc. ) precum si forma de organizare individuala, care capata în unele situatii, o semnificatie aparte în logica desfasurarii învatamântului matematic .

În conditiile unui învatamânt modern , optimul organizatoric nu poate fi dictat printr-o norma didactica, ci el este rezultatul deciziei învatatorului pentru fiecare situatie didactica în parte. Nivelul cel mai înalt de activitate matematica îl reprezinta activitatile în care se lasa elevilor independenta deplina în compunerea si rezolvarea pe cai diferite a exercitiilor si problemelor .

La toate aceste niveluri, activitatea matematica a elevilor trebuie stimulata si sustinuta de catre învatator , prin repartizarea unor fise cu sarcini diferentiate, prin control si evaluare sistematica a rezultatelor .Deci putem spune ca ,în realizarea unui învatamânt activ, formativ al matematicii un rol important îl are munca independenta a elevilor. Construirea unui sistem de exercitii si probleme judicios gradate sub aspectul efortului mintal pe care îl solicita elevi si rational programate atât în suita de lectii ,cât si în cadrul secventelor fiecarei lectii, conduce la formarea si consolidarea deprinderilor de calcul si de rezolvare de probleme, concomitent cu dezvoltarea psihica a elevilor.

Îmbinarea formelor de activitate-frontala, pe microgrupuri si individuala, creeaza posibilitati largi pentru mobilizari multiple si variate ale elevilor în procesul învatarii matematicii.

Nu se poate vorbi de activizarea elevilor, fara a se avea în vedere individualizarea procesului de predare-învatare si evaluare .Este vorba de o activizare diferentiata pe fondul unei individualizari corect practicate. Individualizarea si tratarea diferentiata a elevilor constituie doua dintre strategiile principale de ameliorare a randamentului scolar si de înlaturarea esecurilor .

Individualizarea si abordarea diferentiata a procesului de instruire la matematica presupune , pe de o parte, cunoasterea elevilor, investigarea lor permanenta si urmarirea evolutiei lor ( mai ales pe plan intelectual) , pentru a le pute adresa în orice moment sarcini corespunzatoare nivelului lor real de dezvoltare . Pe de alta parte, individualizarea si tratareadiferentiata presupune o buna cunoastere a continutului de predat si respectarea cerintelor unitare pe care le exprima programele scolare .

Strategia individualizarii si diferentierii învatamântului matematic conduce la o gama foarte variata de forme de lucru si modalitati de organizare a activitatii de învatare . Se impune ca învatatorul sa gândeasca asupra modalitatilor de îmbinare a celor trei forme de activitate (frontala, în grup si individuala ), iar în cadrul fiecareia dintre acestea asupra unor sarcini unitare, gradate însa prin continut si mod de realizare .În raport de capacitatile fiecarui elev, de cerintele unice ale programei scolare se pot formula implicit niveluri de efort diferite (recunoastere, reproducere, integrare ,transfer, creativitate) .Important este ca în toate formele de activitate matematica pe care le desfasoara elevii ( la tabla, pe caiete, pe fise individuale), învatatorul sa urmareasca aplicarea întregului sistem diferentiat al variabilelor acestor activitati : obiective , continuturi, moduri de realizare a sarcinilor, forme de evaluare etc.

Instruirea si educarea matematica, activitate cu obiective precis determinate, necesita organizarea si coordonarea componentelor care concura la atingerea obiectivelor .

Forma principala de organizare a procesului instructiv-educativ la matematica este lectia "în cadrul careia elevii desfasoara o activitate comuna de învatare sub conducerea educatorului, într-o anumita unitate de timp-ora scolara

Lectia trebuie privita ca activitate , ca proces, care îmbina didactic metoda, mijloace si tehnici de învatamânt cu respectarea principiilor didactice .

Tipul lectiei corespunde scopului lectiei .Variantele lectiilor de matematica se realizeaza dupa obiectivele operationale .Ioan Nicola (28) prezinta urmatoarele tipuri de lectie :

A. Tipul lectiei mixte sau operationale;

B. Tipul lectiei de comunicare (cu urmatoarele variante .descoperirea pe cale inductiva, descoperirea pe cale deductiva, introductive, prelegere, seminar, problematizate, dezbatere, de asimilare a noilor cunostinte, bazate pe instruirea programata ) ;

C. Tipul lectiei de formare a priceperilor si deprinderilor ;

D. Tipul lectiei de recapitulare si sistematizare (de fixarea sau consolidare ).

Lectia de predare-învatare-evaluare, varianta de comunicare prin dobândire de cunostinte.

Aceasta lectie are sarcina didactica principala , însusirea unor cunostinte noi si fixarea lor.

Captarea atentiei este deseori neglijata sau formal rezolvata, considerându-se ca prin anuntarea obiectivelor lectiei sau prin restabilirea linistii, atentia elevilor a fost captata . Ea ve putea fi realizata prin întrebuintarea unei forme care sa stârneasca interesul sau chiar sa-i socheze pe elvii clasei respective. Datorita caracterului abstract al matematicii nu se pot gasi la orice lectie legaturi cu o preocupare familiara lor, dar trebuie gasita o fraza , o întâmplare , o povestire, un exercitiu, un joc prin care sa se stârneasca interesul asupra activitatii care se va realiza în lectie .

Enuntarea obiectivelor urmarite trebuie prevazute si ea ca etapa, pentru ca elevii sa fie constienti despre ce se urmareste în lectia respectiva .

Reactualizarea celor învatate anterior are rolul de a împrospata acele cunostinte anterior studiate necesare întelegerii noilor continuturi . Se pot rezolva diverse problem care sa faca elevul sa intuiasca existenta faptului matematic nou, care reprezinta noile cunostinte .

Prezentarea noului continut si dirijarea învatarii sunt etape care se produc concomitent si ocupa cea mai mare parte a lectiei .

Asigurarea feedback-lui arata elevului nivelul la care a ajuns si se poate realiza fie prin reproducerea celor învatate fie printr-o fisa de lucru . Pentru învatator este o etapa de mare importanta, caci permita analiza rezultatelor lectiei prin prisma atingerii obiectivelor stabilite.

Intensificarea retentiei, asigurarii transferului se realizeaza prin probleme variate sau prin descoperirea cunostintelor studiate, aplicate.

Lectia prin instruire programata are cu totul alta forma . În acest sens toate sarcinile sunt preluate de un program ,noile cunostinte sunt transmise cu ajutorul acestuia, având dificultati descompuse în asa fel încât sa poata fi întelese de catre toti elevii . Exercitiile din program si secventele de recapitulare asigura retentia si transferul, iar unele exercitii date fara raspuns si fara puncte de sprijin .

Învatarea prin descoperire utilizata pentru însusirea unor cunostinte determina si ea o varianta a acestei lectii. Frecventa acestor lecttii de predare-învatare-evaluare, varianta a formarii priceperilor si deprinderilor , în predarea matematicii este foatre mare si de numarul si atentia acordata lor de propunator depinde în mare masura succesul muncii la catedra , al educatorului . Aceste lectii urmaresc retinerea materialului însusit si aplicarea lui în exercitii si probleme cât mai variate .

Învatamântul matematic si dezvoltarea rationamentului nu se poate realiza

fara cunostinte sistematice si bine consolidate. Recapitularea materiei se face cu scopul retinerii materialului studiat, asigurarii transferului si a eliminarii lipsurilor. Se impune deci recapitularii sa respecte anumite conditii :

● Sa nu se repete materia în acelasi fel în care sa predat, ci sa se faca o sinteza a temelor principale si daca se poate sa se stabileasca noi legaturi între acestea. Elementul de noutate este de mare importanta pentru trezire interesului , caci o reluare în aceeasi ordine nu ar putea fi decât plictisitoare.

● Lectiile de recapitulare trebuie anuntate din timp si antrenati toti elevii într-o munca de recapitulare. Pentru a nu inhiba cu nimic activitatea elevilor este preferabil sa nu fie notati . Planul de recapitulare poate fi dat elevilor fie cu o ora înainte , pentru a putea revedea independent materia pe baza lui, fie sa se elaboreze la începutul lectiei. Exercitiul are pentru elevi un caracter de creatie si prin aceasta produce o mai mare satisfactie .

● Varianta lectiei de evaluare care urmeaza în mod firesc lectiei de recapitulare si care ca sarcina dominanta verificarea si aprecierea cunostintelor elevilor prin prisma obiectivelor operationale anterior fixate .Ea vizeaza atât îndeplinirea obiectivelor informative, adica a cuantumului de cunostinte teoretice, cât si a celor formative, adica a modului în care elevul poate opera cu aceste cunostinte teoretice prin rezolvarea de probleme complexe.

● Lectia de verificare se realizeaza în doua moduri .

1) lectia de verificare orala;

2) lectia de verificare scrisa, care are doua etape: efectuarea lucrarii si analiza ei .

Lectia de verificare orala se aseamana ca structura cu lectia de recapitulare . Deosebirea consta în faptul ca daca în lectia de recapitulare atentia este focalizata spre sistematizarea materiei, în lectia de verificare ne intereseaza modul în care elevii si-au însusit materia, limbajul matematic, precum si aplicarea acestor cunostinte în rezolvarea problemelor. În lectia de verificare orala este bine sa se stabileasca înainte ce se va asculta si materia care va face obiectul interogarii fiecarui elev în parte .

Lectia de verificare scrisa are urmatoarea srtuctura : organizarea clasei pentru desfasurarea lucrarii scrise ; anuntarea temei; desfasurarea lucrarii scrise .

Organizarea clasei trebuie facuta în asa fel încât sa se asigure posibilitatea fiecarui elev de a lucra independent pentru a se putea aprecia cunostintelor reale ale fiecaruia. Este bine ca itemii sa se dea diferentiat pe numere. Subiectele trebuie astfel alese încât sa cuprinda partile mai importante ale materiei parcurse .Gradul de dificultate sa fie potrivit dar, sa permita verificarea obiectivelor propuse atât în ceea ce priveste dezvoltarea rationamentului matematic cât si gradul de formare a deprinderilor de calcul.

A doua etapa a acestei lectii o constituie analiza lucrarilor scrise, analiza ce trebuie sa asigure ca pe viitor elevii sa poata efectua corect o tema asemanatoare cu cea propusa. Structura unei astfel de lectii este . aprecierea generala a lucrarilor, stabilirea greselilor si explicarea cauzelor care le-au determinat, analiza câtorva lucrari mai reprezentative, distribuirea lucrarilor si corectarea individuala .

CAPITOLUL II

Notiuni fundamentale în aritmetica

II.1. Elemente de logica matematica.

Propozitii adevarate sau false.

Un text matematic este alcatuit din propozitii redactate în cuvinte sau cu ajutorul simbolurilor matematice .

Definitie : Se numeste propozitie un enunt despre care putem spune ca este adevarat sau fals însa nu amândoua simultan .

Propozitiile simple se noteaza , de obicei cu p, q , r, ... sau indexate .

Negatia unei propozitii p este o alta propozitie "non p " care este adevarata când p este falsa si falsa când p este adevarata .

Implicatia logica

Se numeste ca "propozitia p implica propozitia q (sau ca din p rezulta q) si se scrie "p =>q", daca ori de câte ori este adevarata propozitia p, este adevarata si propozitia q .

Semnul "=>"se citeste "implica" sau "rezulta".

Echivalenta logica

Se spune ca "propozitia p este echivelenta cu propozitia q " si se scrie "p q", daca p=>q si q=>p, adica daca propozitiile p si q sunt simultan adevarate (sau false).

Semnul se citeste "echivalent" sau "daca si numai daca" .

Disjunctia

Legînd doua propozitii date p, q prin "sau" obtinem o noua propozitie "p sau q", numita disjunctia lor .

"p sau q" este adevarata atunci când cel putin una din cele doua propozitii este adevarata (neexcluzându-se cazul când ambele propozitii sunt adevarate ).

Conjunctia

Legând doua propozitii date p, q prin "si" obtinem o noua propozitie "p si q " numita conjunctia lor.

"p si q " este adevarata , atunci ambele propozitii sunt adevarate .

II.2.Multimi. Operatii cu multimi.

În limbajul matematic , notiunea de multime se refera la o colectie de obiecte distincte si precis specificate. Dupa matematicianul german Georg Cantor, parintele teoriei multimilor, "o multime este o ansamblare de anumite obiecte , distincte, ale intuitiei sau gândirii noastre într-un singur tot".

Multimile se noteaza în general cu litere mari din alfabetul latin : A.M.X. etc, iar obiectele componente ale acestora se numesc elemente ale multimii si se noteaza cu litere mici: a , m , x etc.

O multime poate fi data în doua moduri :

a) Prin specificarea unei proprietati pe care o au toate elementele multimii respective si pe care nu o au alte obiecte (elemente)-analitic :

A = multimea elevilor din clasa;

B = multimea muncitorilor din România ;

C = multimea literelor din alfabetul latin s.a.m.d.

b) Prin enumerarea elementelor componente (simbolurile lor fiind scrise într-o acolada) -sintetic:

D =, multimea cifrelor arabe;

E = , multimea formata din numarul natural 5 e.t.c.

Multimea care nu contine nici un element se numeste multime vida si se noteaza cu "ø".

Daca elementul a apartine multimii A, acesta se scrie "a A".

Daca elementul a nu apartine multimii a, acesta se scrie : "a A ".

Dintre multimile de numere fac parte :

►Multime numerelor naturale :

N =

►Multimea numerelor naturale fara 0 :

N * =

►Multimea numerelor naturale pare :

N2k =

►Multimea numerelor impare :

N2k+1 =

►Multimea numerelor întregi :

Z =

►Multimea numerelor rationale:

Q =

►Multimea numerelor irationale (I) un numar irational (pozitiv sau negativ) este un numar care poate fi reprezentat cu ajutorul unui numar zecimal cu un numar infinit de zecimale, care se succed periodic ;

►Multimea numerelor reale (R) un numar real este un numar care apartine fie multimii numerelor rationale ,fie multimii numerelor irationale .

Despre doua multimi A si B se poate spune ca sunt egale, daca orice element a lui A apartine lui B si orice element a lui B apartine lui A.

Trebuie facuta distinctia între multimi egale (care au acelasi element) si multimi cu acelasi numar de elemente, care se numesc echipotente .

Relatia de egalitate a multimilor are urmatoarele proprietati :

a) este reflexiva , adica A=A, pentru orice multimeA;

b) este simetrica : daca A=B, atunci B = A;

c) este tranzitiva : daca A = B si B = C, atunci A = C .

Spunem ca o multime A este inclusa într.o alta multime B, daca orice element al multimii A apartine multimii B. În acest caz scriem A B, iar multimea A se mai numeste si submultime a multimii B.

Dintre submultimile unei multimi A, multimea A si multime vida se numesc submultimi improprii ale multimii A, iar celelalte se numesc submultimi proprii ale multimii A.

Multimea tuturor submultimilor unei multimi date A se numeste multimea partilor lui A si se noteaza P (A).

Relatia de incluziune are urmatoarele proprietati :

a) este reflexiva ,adica A A, pentru orice multime A ;

b) este asimetrica , adica AÌB si BÌA atunci A = B;

c) este tranzitiva,adica A B si B C =>A C.

Uneori este nevoie sa se foloseasca o multime notata E si numita multime de referinta sau multime totala . În anumite cazuri , se da explicit , în altele se subântelege (în multimea A =,multimea de referinta este multimea numerelor naturale ).

Operatii cu multimi :

a) Reuniunea a doua multimi A si B este multimea tuturor elementelor care apartin cel putin uneia din multimile A sau B . Se noteaza A U B si se citeste "A reunite cu B" .

Folosind scrierii cu simboluri , avem : .

b)Intersectia a doua multimi A si B nu au elemente comune, daci A ∩ B si se citeste "A intersectat cu B".

Scriind cu simboluri , avem :.

Daca doua multimi A si B nu au elemente commune, deci A ∩ B = ø ,aceste multimi se numesc disjuncte .

c)Fiind data o multime E si o submultime a sa A, numim complementara lui A în raport cu E ( si notam C A) multimea elementelor din E care nu apartin lui A. În limbaj formalizat scriem : C A=.

d) Diferenta multimilor A si B este multimea elementelor care apartin multimii A, dar nu apartin multimii B . Deci A/B =

e) Produsul cartezian al multimilor A si B (notata A/B sau A-B) este multimea ale caror elemente sunt toate perechile ordonate (a,b), în care a A si b B si se noteaza AxB.Deci AxB=

Operatiile cu multimi au urmatoarele proprietati :

" A E A U f = A " A E A ∩ E = A

f ) legile lui Morgan : daca A si B sunt submultimi ale unei multimi E, atunci : C (A U B ) = C A C B C ( A B ) = C A U C B

g) distributivitatea produsului cartezian fata de reuniune si intersectie:

A x ( B U C ) = ( A x B ) U ( A x C )

A x ( B C ) = ( A x B ) ( A x C )

În ceea ce priveste multimile echipotente, multimile A si B sunt echipotente daca exista o aplicatie bijectiva între A si B. Se scrie A ~B si se citeste "A este echipotent cu B".

Proprietatile echipotentie multimilor :

a) este reflexiva, multimea A este echipotenta cu ea însasi , deoarece avem aplicatia identica f:A→A, care este bijectiva "a A, f(a) = a, A ~A;

b) este simetrica daca f:A→B este bijectiva, atunci exista aplicatia inversa f^-1:B→A ; deci A ~B, B ~A

este tranzitiva daca f: f:A→B si g : B→C A ~B si B~C si A C

Având aceste proprietati, relatia de echipotenta este o relatie de echivalenta si împarte multimile în clase .

O clasa de echivalenta , definita de relatia de echipotenta, se noteaza printr-un symbol, care se numeste numar cardinal sau "puterea" fiecarei multimi din clasa respectiva .

Daca multimile A si B sunt echipotente, ele au aceeasi putere si li se asociaza acelasi numar cardinal. Notam cardinalul multimii A cu A .

II.2. Relatii. Functii .Proprietati.

A.Relatii.

Fiind date doua multimi A si B se numeste relatie binara între elementele multimii A si elementele multimii B , o propritate R a perechii ordonate (x,y=), unde x A si y B.

Daca perechea (x, z), x A si y B are proprietatea R , atunci se spune ca x este in relatie R cu y si se scrie x R y (elementul x A îi corespunde elementului y B).

Multimea tuturor cuplurilor care au proprietatea R determina o parte a produsului cartezian AxB, numit graphic (cu graf) al relatiei R.

O relatie se poate pune în evidenta printr-o diagrama.

Daca doua multimi A si B sunt egale (A=B) atunci R este o multime binara între elementele multimii A sau relatiei binare pe A.

O relatie binara R între elementele unei multimi A se numeste relatie reflexiva, daca propozitia xRx este adevarata pentru orice x Î A.

O relatie binara R între elementele unei multimi A se numeste relatie simetrica , daca fiind adevarata propozitia xRy, este adevarata si propozitia yRx, pentru x,yÎA, scriem xRy yRx, unde x,yÎA.

O relatie binara R între elementele unei multimi A se numeste relatie tranzitiva, daca ori de cate ori sunt adevarate xRy si yRx, este adevarata si relatia xRz.

O relatie care este reflexiva, simetrica si tranzitiva se numeste relatie de echivalenta.

Multimea tuturor elementelor y A care satisfac proprietatea xRy poarta numele de clasa a elementului x.

O relatie binara R între elementele unei multimi A se numeste relatie de ordine, daca este reflexiva, asimetrica (adica xRy si yRx x=y) si tranzitiva.

B. Functii.

Fiind date doua multimi A si B si un procedeu prin care se asociaza oricarui element x A si un element y B, numai unul singur, spunem ca am definit o functie pe A cu valori in B. Scriem f:A B.

Multimea A se numeste domeniu de definitie al functiei, iar B multimea in care functia ia valori sau codomeniu.

Daca elementul x A îi asociem elementul y B, spunem ca y este imaginea lui x prin functia f si scriem y=f(x).

Relatia binara y=f(x) între elementele multimii A si elementele multimii B se mai numeste lege de corespondenta.

Deci, o lege este definita de trei elemente:

►domeniu de definitie

►codomeniul

►lege de corespondenta.

Legea de corespondenta poate fi data în doua moduri:

►sintetic (tablou, diagrama)

►analitic (una sau mai multe expresii).

Daca multimile A si B sunt multimi de numere reale, atunci functiile definite pe A cu valori în B se numesc functii numerice.

Pentru aceste functii graficul format din acea parte a produsului cartezian care contine perechile (x, f(x)), se poate reprezenta geometric în plan.

O functie f:A B este injectiva, daca pentru orice x₁, x₂ ÎA cu x₁ x₂ avem f(x₁) f(x₂).

O functie f:A B este surjectiva daca pentru orice y B exista cel putin un x A astfel încât y=f(x). Cu alte cuvinte, orice element din B reprezinta o valoare a functiei , o imagine a unui element din A , deci B=f(A).

Functiile care sunt injective si surjective se numesc bijective.

Fie f:A B si f:B C. Functia h:A C pentru care h(x)=g(f(x)), oricare ar fi x A, se numeste functie compusa a functiilor g si f si se noteaza f=g0f.

Compunerea functiilor nu este comutativa (g0f≠f0g).

Functia 1_A:A A data prin 1_A:(A)=x oricare ar fi x A , se numeste functie identica. Aceasta functie are proprietatile 1_A0f=f si f01_A=f pentru orice functie f.

O functie f:A B se numeste ireversibila daca exista o functie notata f^-1, astfel încât f^-1 :B A, f^-10f=1_A si f0f^-1 =1_B.

O functie este ireversibila daca si numai daca este bijectiva.

II.3. Numere naturale. Operatii cu numere naturale. Proprietati.

A.Numar cardinal.

O clasa de echivalenta , definita de relatia de echipotenta, se noteaza printr-un simbol care se numeste numar cardinal.

Daca multimile A si B sunt echipotente , ele au aceeasi putere si li se asociaza acelasi numar cardinal. Notam cardinalul multimii A cu A.

Adunarea numerelor cardinale

Oricare ar fi multimile A si B disjuncte , prin definitie card (A B)=A+B.

Proprietatile adunarii cardinale:

a). Este comutativa A B=B A A+B=B+A(a+b=b+a);

b). Este asociativa considerând multimile A,B,C disjuncte doua câte doua, avem (A B) C=A (B C) (A B) CA (B C) (A+B)+C=A+(B+C) ((a+b)+c=a+(b+c))

c). Are element neutru: cardinalul 0(al multimii vide)

A A=A A A 0+A=A+0=A (o+a=a+0=a)

Înmultirea numerelor cardinale

Oricare ar fi multimile A si B avem prin definitie : card (AxB=A●B)

Proprietatile înmultirii cardinalilor :

a).este comutativa AxB ~ BxA AxB =BxA A●B=B●A (a●b=b●a);

b)este asociativa (AxB)xC~Ax(BxC) (AxB)xC=Ax(BxC) (A●B) ●C=A●(B●C) ((a●b) ●c=a●(b●c));

c) cardinalul 1 este elemental neutru fie N=.

AxN ~ NxA ~A AxN=NxA=A Ax1=1xA=A

d)înmultirea oricarui cardinal cu 0 da rezultatul 0 Ax Ø= ØxA Ax Ø ~ Ø Ax Ø = Ø Ax0=0

e) este distributiva fata de adunare Ax(B C)= (AxB) (AxC) Ax(B C) ~ (AxB) (AxC) Ax(B+C) =AxB+AxC

B.Numar natural.

Cardinalul a este finit daca a ≠ a+1 . Daca un cardinal nu este finit sau transfinite.

Multimea simbolurilor care reprezinta cardinalele finite se numeste multimea numerelor naturale si se noteaza cu N.

N = , N^*=.

Teorema : daca a+1=b+1, atunci a=b.

Fie multimea M , care are cardinalul a+1=b+1.

Exista multimile A si B , care îndeplinesc conditia M=A =B

Putem contrui aplicatia bijectiva f:A B , în care avem f(u)=v. Facem o restricte a aplicatiei f excluzând din domeniul de definitie pe u si din codomeniu pe v .

Ramâne functia bijectiva f:A B. Deci A~B si A=B . Atunci card (AU )=a+1 A=a a=b; card (BU)=b+1 B=b.

Teorema : daca numarul natural a este finit, atunci si a+1 este finit .

Presupunem ca a+1 nu este finit. Atunci avem : a+1=(a+1)+1, iar din teorema anterioara rezulta ca a =a+1, adica a nu ar fi finit , ceea ce contrazice ipoteza.

Schematic, inductia matematica se prezinta astfel : P(a) este adevarata .

Ipoteza :P(n) se presupune adevarata .

Concluzia P(n+1) sedemonstreaza ca este adevarata .

Folosind inductia, se demonstreaza ca numerele naturale sunt si regulate fata de adunare (adica , daca a+n=b+n , atunci a =b) si numerele multimii N* sunt regulate fata de înmultire (adica, daca axn=bxn, atunci a=b).

Adunarea si înmultirea numerelor naturale verifica aceleasi proprietati ca si adunarea si înmultirea cardinalilor .

B.1. Relatia de ordine totala

Spunem ca a este cel mult egal cu b si sciem a ≤b , daca exista un numar natural c astfel încât sa avem b=a+c .

Proprietati :

b) a ≤ b, deoarece b = a+e; b ≤ c , deoarece c =b + d .

Adunând ultimele doua egalitati , avem b+c=a+b+d+e c=a+(d+e) c=a+f a≤ c.

Adunând ultimele doua egalitati , avem a+b=a+b+c+d c d.

Numerele c si d fiind naturale , ultima egalitate este valabila numai daca c=d=0.Deci , a=b (antisimetria).

adunarea a doua numere naturale este tot un numar natural ( se spune ca în N adunarea este parte stabila) , deci " a, bÎN Þ a+b ÎN

" a, bÎN , a + b) b + a ;

" a ,b , c Î N avem (a + b ) +c = a +( b + c) ;

" aÎN , avem a + 0 = 0 + a = a.

Asociativitatea poate fi folosita cu succes în calculele mintale .

Exemplu : 1+2+3+.+ 97+98+99+100 = 100+(1+99)+(2+98)+(3+97) +.=(100x99) : 2+100= (100 x 101) : 2.

B.2.2.Scaderea

A scadea doua numere a si b , primul numit descazut, al doilea scazator, înseamna a gasi un numar , numit rest sau diferenta, care adunat cu scazatorul sa ne dea descazutul. Operatia se noteaza cu semnul "-" . În felul acesta , se mai spune ca

scaderea este operatia inversa adunarii. Avem deci a - b = x , daca b + x = a . În multimea numerelor naturale operatia de scadere este posibila numai daca a ≥ b .

Proprietati si reguli de calcul .

" a,b Î N , avem a +b - b = a ;

b) Pentru a scadea un numar dintr-o suma este suficient sa-l scadem dintr-un termen al sumei : a + b+ c + d - m = a+ b+ (c - m) + d ,c > m

c) Daca marim si descazutul si scazatorul cu acelasi numar , diferenta nu se schimba : (a + c) - (b + c)= a - b ;

d) Daca micsoram si descazutul si scazatorul cu acelasi numar , diferenta nu se schimba : (a - c) - (b - c) = a - b ;

e) Daca scazatorul creste sau scade cu un numar , atunci si diferenta creste sau scade cu acelasi numar : a - (b + c ) = a-b-c ; a - (b -c ) = a - b +c ;

f) Daca descazutul creste sau scade cu un numar , atunci si diferenta creste sau scade cu acelasi numar : (a + c) - b = (a - b) + c ; (a - c) - b = (a - b ) -c ;

B .2.3. Înmultirea

A înmulti doua numere a si b , primul numit deînmultit, al doilea înmultitor, înseamna a afla suma a "b" termenilor egali cu a : a x b = a +a + a + .+ a , b termini

Tot prin definitie a x1 = a si a x 0= 0

Numerele care se înmultesc se numesc factori , iar rezultatul se numeste produs .

Proprietati :

" a,b ÎN ;

" a,b,c ÎN ;

" a,b,c ÎN ; numarul 1 este element neutru ax 1 = 1 x a , " a, ÎN ;

Reguli de calcul

a) într-un produs de mai multi factori putem schimba oricum ordinea lor , fara ca produsul sa se schimbe ;

b) într-un produs de mai multi factori putem înlocui doi sau mai multi factori prin produsul lor;

înmultirea este distributiva fata de scadere : a x(b - c ) = a x b - a x c ," a,b,c ÎN ; ( b>c) ;

e) daca un factor al produsului se înmulteste de n ori , produsul se mareste tot de n ori .

B.2.4. Împartirea

A împarti doua numere a si b , primul numit deîmpartit , al doile numit împartitor , înseamna a gasi un numar numit cât , care împartit cu împartitorul sa rezulte deîmpartitul .

Împartirea lui a la b se scrie a:b sau a /b .

Împartirea este operatia inversa înmultirii . Ea nu este întotdeauna posibila . Când împartirea este posibila câtul este unic . Împartirea la 0 nu este posibila .

Aceasta operatie poate fi vazuta ca si o scadere repetata . Cu ajutorul multimilor, ea se pune în evidenta astfel : fiind data o multime A cu elemente , formam submultimi disjuncte , fiecare având acelasi numar de elemente .

Se pun în evidenta doua procedee de împartire :

►împartirea prin cuprindere este procedeul prin care, cunoscând numarul de elemente al submultimii B , trebuie sa aflam numarul de submultimi ;

► împartirea în parti egale este procedeul prin care , cunoscând numarul de elemente al multimii A si numarul de submultimi B , trebuie sa aflam numarul de elemnte dintr-o submutime .

Teorema împartirii cu rest :

" a,b ÎN , ( b ≠ 0), exista doua numere naturale q si r numit respectiv cât si rest , astfel încât :a = b x q + r , r < b ( D = Î x Q +R ) . Numerele q si r determinate de aceste conditii sunt unice .

Când restul este 0 , spunem ca avem o împartire exacta .

Proprietati si reguli de calcul

e) pentru a împarti un numar la un produs, împartim pe rând la fiecare factor al produsului ;

f) pentru a împarti un numar la alt produs , se efectueaza mai întâi simplificarile ;

g) pentru a împarti o suma sau o diferenta la un numar , putem împarti fiecare termen la acel numar : ( a + b -c ) : m = a: m + b : m - c : m ;

Termenul de fractie se gaseste în manualele europene medievale ca o traducere din araba , unde înseamna rupere .

Cele mai importante operatii cu fractii din manualele medievale si ale Renasterii sunt înmultirea, împartirea si adunarea la acelasi numitor. De-abia în secolul al-XVI lea apare aceasta tehnica pe care o impunem elevilor astazi.

Întorcandu-ne în timp constatam ca teoria fractiilor a dat nastere la multe dificultati de întelegere, deoarece unele din operatiile lor nu se aseamana cu analoagele din multimea numerelor naturale, fara a mai vorbi de operatiile cu numere rationale negative.

Daca adunarea si înmultirea nu dau loc la probleme de existenta a rezultatelor, care sunt totdeauna tot numere naturaele, scaderea si împartirea pun astfel de probleme, care au necesitat eforturi de întelegere.

Scaderea a adus la introducera numerelor negative si a lui 0, întâi ca simbol si apoi ca numar, îmbogatind prin aceste extinderi multimea numerelor naturale , prin aceste noi numere, ca sa devina multimea numerelor întregi pozitive, negative si completata cu 0 ca numar.

Împartirea este cunocuta ca o operatie nascuta din practica împartirii unei pâini în parti egale sau a unui teren între mai multi mostenitori. În primul rând împartirea în mai multe parti egale necesita întelegerea notiunii de parte: o jumatate, un sfert, o treime, dintr-un întreg si un numar fractionar, ca numere care exprima împartirea a doua numere cand acestea nu se fac exact.

Desi relatia dintre înmultire si împartire era cunoscta înca din antichitate, ca prima este inversa celei de-a doua, împartirea cu o fractie se explica independent , folosindu-se ca justificare , analogia.

Fractii ordinare

La multimea numerelor rationale se poate ajunge pe doua cai care pot fi reprezentate schematic prin :

1). Numere naturale , fractii pozitive, fractii negative , numere rationale (N, Q₊,Q_-,Q) :

2). Numere naturale,numere întregi, numere rationale (N, Z, Q).

În scoala se porneste de la notiunea de unitate fractionara.

Definitia 1 : numim unitate fractionara o parte dintr-un întreg împartit în parti egale (ceia ce se noteaza

Definitia 2 : (A fractiei ordinare). Un numar natural m de unitati fractionare din întregul u se numeste fractia din u.

Numarul m de unitati se numeste numaratorul fractiei.

Numarul n ce ne arata în câte parti egale a fost împartit întregul se numeste numitorul fractiei.

Multimea tuturor fractiilor definite anterior poarta denumirea de nultimea numerelor rationale pozitive.

Definitia 3 : fiind date doua numere intregi a si b , b≠0 , ele determina un numar x care satisface conditia bx=0. Numarul x se noteaza prin simbolul si se numeste numar rational .

Definitia egalitatii : fiind date doua numere întregi a si b≠0 exista un numar x definit prin simbolul ,astfel încât bx=a.

Definitia 4 : doua fractii sunt egale atunci si numai atunci când ele provin din amplificarea aceleiasi fractii ireductibile.

Operatii : adunarea: fie x₁ si y₁ solutii unice ale ecuatiilor b x₁=a si d y₁ =c. Prin înmultirea cu d si respectiv b a celor doua ecuatii, avem bdx₁=ad, bdy₁=bc iar prin adunare obtinem bd(x₁+y₁)=ad+bc, de unde x₁+y₁=

Scaderea: se defineste ca operatie inversa adunarii.

Ecuatia are solutia x =

Înmultirea dintre

Împartirea se defineste ca operatie inversa inmultirii.

Reprezentarea pe axa a numerelor rationale pozitive

Pentru a reprezenta un numar rational pe axa procedam astfel : împartim segmental 0-1 în parti egale. Consideram punctul A pe axa astfel încat segmentul [ 0A ] sa cuprinda a segmente egale (cu a n-a parte din o-1), punctual A fiind de aceeasi parte cu 1.

Numarul se reprezinta prin simetricul punctului A fata de O . Fiecarui numar rational îi corespunde pe axa un punct bine determinat si totodata un vector care uneste punctual O cu acest punct.

La doua fractii rationale egale între ele , corespunde acelasi punct pe axa. Fie numerele pozitive

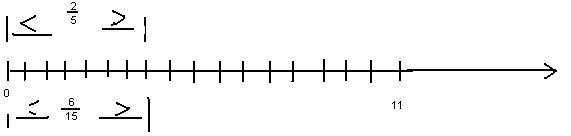
Compararea numerelor rationale pozitive

a) Compararea numerelor rationale cu unitatea

Daca >1 a>b,fractia este supraunitara.

Daca a=b , fractia este echiunitara .

Daca <1 a<b, fracti este subunitara .

b) Compararea numerelor rationale pozitive

-Dintre doua fractii diferite care au acelasi numitor este mai mare aceea care are numaratorul mai mare (>> daca a >b);

-Dintre doua fractii diferite care au acelasi numarator, este mai mare aceea care are numitorul mai mic (> daca a <);

-Dintre doua fractii care au numaratori si numitori diferiti se pot compara dupa metoda proportiilr si anume : daca produsul mezilor este mai mare decât produsul extremilor , atunci prima fractie este mai mare decât a doua si invers:

Daca ad >bc atunci >

Amplificarea si simplificarea numerelor naturale

Operatia prin care se maresc ambii termini ai fractiei de acelasi numar de ori se numeste amplificare iar operatia prin care se micsoreaza ambii termini de acelasi numar de ori se numeste simplificare .

Observatii : Prin operatiile de amplficare si simplificare se obtin fractii echivalente. (a,b=1) , se numesc fractii ireductibile .În operatii se lucreaza pe cât posibil cu fractii ireductibile . De asemenea , rezultatele operatiilor se duc la forma ireductibila.

Operatii pe multimea numerelor rationale

Pe multimea Q sunt definite urmatoarele operatii :

a)Adunarea .Pentru a aduna doua numere rationale, ele trebuie sa prezinte unitati fractionare de acelasi fel, deci sa aiba acelasi numitor. Deci pentru a aduna doua sau mai multe numere rationale , întâi se aduc la acelasi numitor se aduna numitorii, numitorul sumei fiind numitor comun .

Numitorul comun a doua sau mai multe fractii este c.m.m.m.c. al numitorilor. Rezulta ca aducerea fractiilor la acelasi numitor propune urmatoarele operatii :

descompunerea numitorilor în factori primi ;

stabilirea c.m.m.m.c. al numitorilor;

amplificarea fiecarei fractii cu câtul dintre numitorul comun si numitorul fractiei respective .

b)Scaderea numerelor rationale . Oricarui cuplu de numere rationale , , i se poate asocia numarul rational -= numit diferenta celor doua numere rationale .Întrucât numarul - este opusul numarului rational se poate spune ca difereata a doua numere rationale este egala cu suma dintre descazut si opusul scazatorului , adica -= + (-)=.

c) Înmultirea . Oricarui cuplu de numere rationale , i se asociaza numarul rational .=, numit produsul celor doua numere . Prin urmare , înmultire a doua numere rationale se face înmultind numaratorii între ei si numitorii întrer ei .

Observatie .Ori de câte ori este posibil , în efectuarea produsului a doua sau mai multe fractii , întâi se opereaza toate simplificarile posibile si numai dupa aceea se trece la înmultirea între ei a numitorilor, apoi a numitorilor . Multimea numerelor rationale împreuna cu înmultirea determina un grup comutativ. Înmultirea numerelor rationale este distributiva fata de adunare . Toate acestea arata ca multimea numerelor rationale determina fata de adunare si înmultire un corp comutativ .

c) Împartirea numerelor rationale se defineste analog cu împartirea numerelor întregi si anume ca operatie inversa înmultirii. Dar în multimea numerelor rationale fiecarui element îi corespunde elementul invers .În cazul particular b = 1, inversul elementului este elementul . Ţinând cont de aceste proprietati consideram ca orice numar întreg se poate scrie sub forma numarului rational cu numitorul 1, împartirea a doua numere întregi a,b se poate scrie a : b = a . .

d) Prin urmare , câtul a doua numere întregi egale cu produsul dintre deîmpartit si inversul împartitorului . Existând aceasta regula asupra numerelor rationale avem : :=.= .=.

CAPITOLUL III

PREDAREA-ÎNVĂŢAREA OPERAŢIILOR ARITMETICE ÎN ÎNVĂŢĂMÂNTUL PRIMAR -APLICAŢII PRACTICE

La clasele I-IV nu se face studiu teoretic al problemei , în sensul definirii operatiilor . Învatatorul va urmari constientizarea de catre elevi a procesului de cunoastere a semnificatiei operatiilor , cât si a principiilor ce sta la baza aplicarii lor an calcul . Pentru aputea îndruma elevii care au înclinatii spre matematica , învatatorul trebuie sa cunoasca cu claritate definitia fiecarei operatii cu numere naturale si proprietasile acestora. Aceste cunostinte teoretice vor facilita formarea notiunii de operatie adunare-scadere, înmultirea si împartirea , la nivelul posibilitatilor de întelegere a elevilor .

III.1.Probleme specifice predarii-învatarii adunarii si scaderii numerelor naturale din cocentrul 0-20

Studiul organizat al operatiilor de adunare si scadere în cocentrul 0-10 se face dupa ce elevii si-au însusit conceptul de numar natural , numeratia si relatia de ordine definita pe multimea numerelor naturale . Se începe cu aceste doua operatii (adunarea si scaderea ) pentru ca ele sunt mai accesibile elevului de vârsta scolara mica, cu un caracter intuitiv pronuntat si corespunde particularitatilor lui de vârsta .

Introducerea operatiilor de adunare si scadere se poate face fie folosind reuniunea a doua multimi disjuncte si diferenta a doua multimi, fie folosind rigletele . Activitatile pe care le desfasoara elevii cu multimi de obiecte si cu riglete (înca de la gradinita )îi pregatesc pentru întelegerea esentei acestor doua operatii . Gândirea copilului va opera prin abstractizare , prin generalizare si prin analogie .

Elevii trebuie sa înteleaga , folosind exemple variate de multimi, ca rezultatul adunarii a doua multimi este cardinalul reuniunii a doua multimi disjuncte finite, iar pe planul operatiilor cu numere (reprezentantii multimilor ce se reunesc) avem o adunare .

Pentru formarea si însusirea notiunii de adunare se porneste de la operatii cu multimi de obiecte concrete uzuale -etapa perceptiva, dupa care se trece la efectuarea de operatii cu reprezentari ce au tendinta de a se generaliza- etapa repezentarilor si în final , se face saltul la conceptul matematic de adunar.

Prima faza-faza concreta este actuinea concreta si nemijlocita cu obiectul cunoasterii .

De exemplu : elevii formeaza o multime cu flori rosii cu trei elemente si o multime cu flori galbene cu 4 elemente. Reunindu-se cele doua multimi cu flori se formeaza o multime care are 7 flori rosii si galbene . Asemanator , reunindu-se o multime formata din 3 mingi (jetoane) cu o multime formata din 4 mingi (jetoane) se formeaza o multime care are 7 mingi (jetoane). Se continua procedeul pâna ce se constientizeaza , la fiecare elev , faptul ca reunind o multime formata din 3 obiecte cu o alta multime formata din 4 obiecte de acelasi fel se obtine o multime formata din 7 obiecte . Se poate continua cu multimi de creioane , flori, braduleti e.t.c.

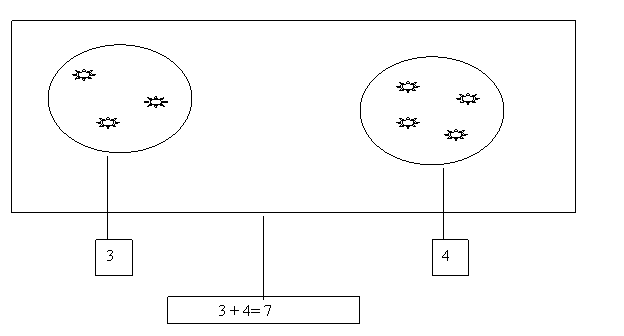
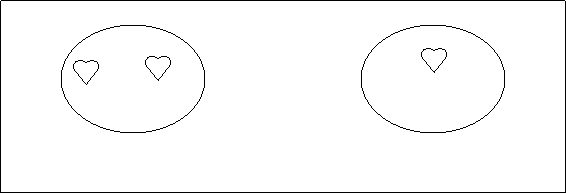
Faza a II-a-semiabstracta , a formarii reprezentarilor imaginativ-concrete

Este etapa reprezentarilor prin simboluri practice , abstractizat-intuitive. Elevii deseneaza pe caietele lor multimi cu simboluri practice.

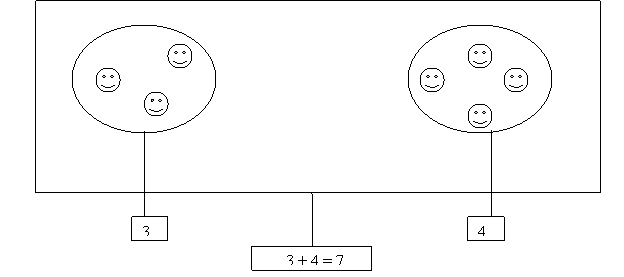
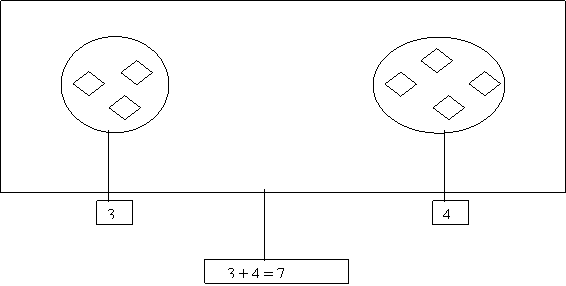
Pe lînga multimile cu simboluri , elevii pot folosi si riglete , ( materiale foarte utile pentru constientizarea simbolurilor numerice). Aceasta etapa este foarte importanta în procesul cunoasterii si are mari valente în întelegerea proprietatilor de comutativitatea a adunarii si de simetrie a relatiei de egalitate .

Se va explica elevilor ca pentru a arata faptul ca am reunit doua multimi ,una cu 3 elemente si alta cu 4 elemente se foloseste semnul (simbolul) "+" , numit plus si care se scrie între numerele ce reprezinta numorul de elemente ale fiecareia dintre cele doua multimi care se reunesc (3+4 si 4+3). Acesta este semnul grafic prin care exprimam în scris operatia de adunare, Deoarece simbolurile grafice 3 +4 si 7 arata , scris sub forma diferita, numarul de elemente ale aceleasi multimi se foloseste între ele simbolul "=" , numit egal si se scrie :3+4=7 , analog si 4+3=7.

În felul acesta elevii îmvata ca 3+4 si 4+3 sunt doua forme de scriere a numarului 7 . Se definesc cele doua numere care se aduna ca fiind termenii operatiei de adunare (primul si respectiv al doilea termen ) si ca rezultatul adunarii îl numim suma .

Deoarece 3+4 si 4+3 reprezinta acelasi numar, deci sumele dintre 3 si 4 si respectiv 4 si 3 sunt egale , spunem ca operatia de adunare are proprietatea de comutativitate . (daca adunam primul termen cu al doilea sau al doilea cu primul rezultatul este acelasi).

Este necesar sa se faca în continuare o serie de exercitii, plecând de la operatii efective cu multimi, trecând prin cele trei etape de actiune, pentru a deduce proprietatea de simetrie a unei egalitati (3+4=7 si 4+3=7 sau 4+3=7 si 7=4+3) , ceea ce exprima faptul ca un numar se poate descompune în suma a doua numere .

Aceasta proprietate se va folosi mult mai târziu în transcrierea simbolica sau exprimarea în scris sau oral a diverselor tehnici de calcul cu numere .

Pentru a motiva elevilor neceistatea efectuarii operatiei de adunare este necesar sa se foloseasca "compunerea" si "rezolvarea" de probleme simple , cu obiecte concrete, uzuale . Exemple:

Ioana are 3 culori galbene si 4 culori rosii . Câte culori are Ioana ?

Dan are 4 mere iar sora lu are 3 mere. Câte mere au cei doi frati?

Costel a cumparat 2 carti . Pe o carte a dat 3 lei iar pe cealalta 4 lei . Câti lei a dat Costel pe cele 2 carti ?

Procedând astfel nu se vor pune probleme de întelegere a operatiei de adunare când introducem în locul unui termen un simbol literal ( a+3=7 ; 3+a=7) deoarece fiecare elev are în planul constiintei un micro-model algoritmic bine fixat prin cele 3 etape succesive (actional -concreta; imaginativ-concreta si simbolica ).

Experienta didactica a demonstrat ca, desi poate micromodulul nu este fixat algoritmic, elevul rezolva cerinta exercitiului prin încercare- eroare sau pe cale probabilistica pâna ajunge la solutie . Aceasta este posibila deoarece actiunea mintala , metoda este formata .

Este necesar sa se îmbogateasca continuu si treptat si limbajul matematic legat de operatia de adunare prin traducere simbolica cu ajutorul adunarii unor operatii concrete exprimate verbal prin "maresc" , "cu" , "adaug", "strâng la un loc", "împreuna cu", "cât trebuie pentru ca", "cât si cu cât" e.t.c.Operatii care se exprima tot prin reuniunea de multimi disjuncte .

Consolidându-se operatia de adunare în concentrul 0-10 a douâ numere ,elevii vor reusi sa adune în acelasi concentru si trei numere . Cu acest prilej se poate introduce si propietatea de asociativitate a adunarii. Acest lucru se realizeaza tot pe baza multimilor. Se va insista asupra faptului ca indiferent în ce ordine se vor aduna trei numere suma lor este aceeasi.

Scaderea numerelor naturale în concentrul 0-10

Se introduce în stransa legatura cu operatia de diferenta dintre o multime si o submultime a sa. Putem spune ca la baza operatiei de scadere sta conceptul de multimi complementare.

Dintr-o multime de obiecte ce au un atribut comun se izoleaza (se îndeparteaza) o submultime de obiecte, ramânând o multime de obiecte cu un numar mai mic decat cel al multimii initiale. si în predarea-scaderii are o foarte mare importanta respectarea celor trei etape: etapa actionala, etapa semiabstracta, etapa formarii conceptelor matematice.

Exemplu:

Se formeaza o multime compusa din 7 figuri geometrice (un dreptunghi, doua patrate si patru triunghiuri).

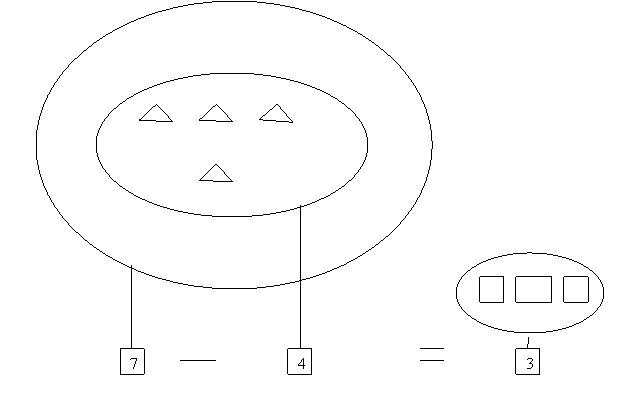
Se grupeaza într-o submultime cele 4 triunghiuri si se îndeparteaza din multimea initial formata. Ramâne astfel o multime nou formata din trei piese
(un dreptunghi si doua patrate).

Se procedeaza la fel cu multimile formate din alte obiecte, flori rosii si galbene, creioane ascutite si neascutite etc.

Se trece apoi la etapa imaginativ-concreta. Daca dintr-o multime formata din 7 obiecte se îndeparteaza o submultime a sa formata din patru obiecte ramâne o multime formata din 3 obiecte. Pentru constientizarea acestei operatii intuitiv-simbolice se poate continua si desena multimi cu diferite simboluri.

Trecându-se la etapa reprezentarilor simbolice, se precizeaza ca simbolul operatiei de scadere este semnul grafic "-" si se citeste minus, ca numarul din care se face scaderea se numeste "descazut" si numarul care se scade este "scazator" si ca rezultatul scaderii se numeste "rest" sau "diferenta" si se scrie 7-4=3.

Prin exemple e scoate în evidenta faptul ca descazutul trebuie sa fie mai mare sau cel putin egal cu scazatorul pentru a se putea efectua scaderea.

Ca si la adunare se pot (chiar este necesar) "compune" si "rezolva" probleme simple atât pentru motivarea introducerii operatiei de scadere, cât si pentru consolidarea acestuia.

În acelasi timp este necesar sa-i obisnuim pe copii sa-si insuseasca formulari de genul "mai putin cu", "dam la o parte", "mai tânar cu", "mai usor cu", "scoatem atât", care se traduc simbolic cu operatia de scadere si cu proba scaderii daca unitatile care au fost luate le reducem la unitatile ramase, reconstituind numarul initial. Adica, adunând restul cu scazatorul obtinem descazutul. Se realizeaza în acest fel si legatura dintre operatiile de scadere si de adunare. Deci : 7-4=3 fiinca 3+4=7.

Predarea si învatarea operatiilor de adunare si de scadere în concentrul 0-20 se realizeaza pe baza cunostintelor însusite si a deprinderilor dobândite anterior de catre elevi, folosind materiale didactice intuitiv-concrete în temeiul unor particularitati specifice numerelor si operatiilor cu aceste numere din concentrul 0-20.

Pentru adunarea uni numar format dintr-o zece si din unitati cu un numar format din unitati si aduna unitatile între ele, apoi rezultatul se aduna cu zecea primului numar.

Având de efectuat adunarea 12+5 procedam astfel: 12 este format dintr-o zece si doua unitati, adica 12=10+2. deci 12+5=10+2+5=10+(2+5)=10+7=17.

Pentru 15+4

Daca din adunarea unitatilor se obtine o zece se explica trecerea peste zece.

De exemplu: 14+6=10+4+6=10+(4+6)-10+10=20 în care zecea obtinuta prin adunarea unitatilor se aduna la prima zece.

Asupra exercitiilor de acest tip trebuie insistat mai mult deoarece adunarea cu trecere peste ordin este o tehnica ce se însuseste destul de greu de catre multi elevi.

Pentru adunarea 7+5 se poate proceda (pâna la însusirea algoritmului prin care se poate spune direct rezultatul 7+5=12) prin completarea primului numar pâna se obsine zece, scop în care se descompune corespunzator al doilea termen al sumei în doua numere care adunate sa dea acest al doilea termen.

Deci pentru adunarea 7+5 se poate proceda astfel: 7+5=7+(3+2)=(7+3)+2=10+2=12. se foloseste în acest fel modalitatea de adunare dintre un numar format dintr-o zece si un numar format numai din unitati.

Pentru adunarea 7+8 se procedeaza la fel (dscompunând de data aceasta primul termen în doua numere a caror suma sa fie 7, în asa fel în cât unul dintre ele adunat cu 8 sa dea o zece) 7+8=(5+2)+8=5+(2+8)=5+10=15

Descompunerea unui termen în suma a doua numere se aplica de obicei numarul mai mic. Este bine ca aceasta descompunere sa se faca pe rând, pentru diferite adunari, atât pentru primul termen cât si pentru al doilea si sa se accentueze de fiecare data ca se foloseste proprietatea de asociativitate a adunarii.

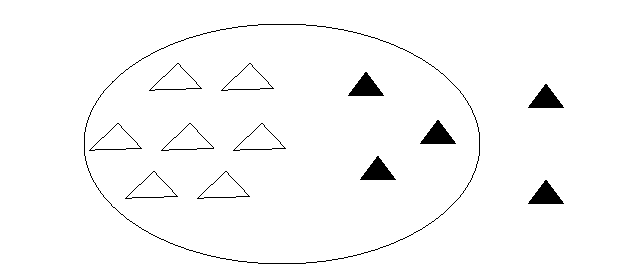
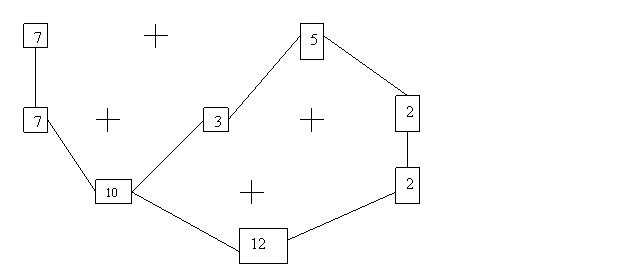
Explicarea adunarii numerelor de tipul 14+7 se poate face si cu ajutorul axei numerelor:

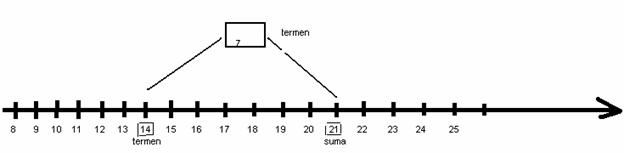
Pentru a consolida aceste cunostinte se pot efectua cu elevii exercitii de tipul:

1 " Scrie opeatiile de adunare corespunzatoare fiecarui desen, apoi rezolva:"

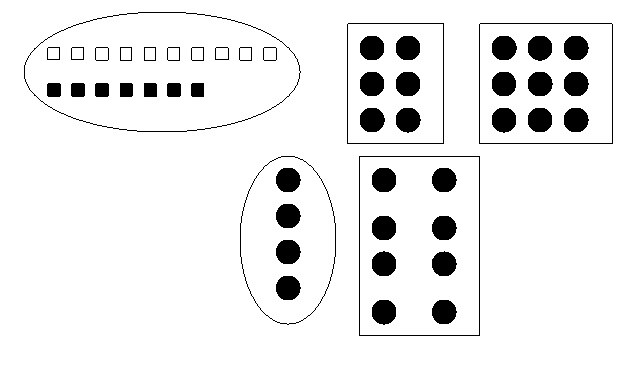
2.Cmpleteaza tabelul :

Termen
termen
suma

Dintre materialele didactice folosite cu succes în predarea adunarii si scaderii numerelor naturale (cu sau fara trecere peste ordin) se pot folosi pe lânga materialul didactic intuitiv si trusa cu tabla si piese magnetice .

Tabla magnetica trebuie sa aiba dimensiuni convenabile pentru a fi vazuta de catre toti elevii clasei . Formele geometrice folosite trebuie sa fie colorate diferit care, prin conventie , sa simbolizeze unitati de un anumit ordin (ex.cercuri negre care sa simbolizeze unitatile, triunghiuri albastre care sa simbolizeze zecile, patrate rosii care sa simbolizeze sutele).

Aceasta trusa cu piese magnetice se poate utiliza: la demonstrarea modului în care se compune si descompune un numar , precum si în operatiile de adunare si de scadere. Ea poate fi folosita sub îndrumare învatatorului, în consolidarea cunostintelor sau atunci când se constata ca nu s-a înteles algoritmul de adunare respectiv scadere .

În predarea-învatarea operatiei de adunare sau scadere este recomandata mai mult scrierea numerelor unul sub altul pentru ca este mai usor înteleasa de catre elevi si usureaza calculele . Învatatorul trebuie sa explice elevilor modul de scriere a termenilor unul sub altul în ordinea: unitati sub unitati , zeci sub zeci, sute sub sute .

Trebuie folosita însa si scrierea în linie sau srierea pe orizontala. Obisnuind elevii cu calcul si folosind ambele modalitati de scriere s-ar putea înlatura dificultatile ce pot sa apara ca urmare a felului în care dunt asezate numerele care se aduna (pe orizontala sau pe verticala).

Pentru predarea-învatarea operatiilor de adunare si de scadere mai ales în cls. I (dar si în clasele urmatoare) se poate folosi cu rezultate foarte bune TRUSA CU RIGLETE (dupa modelul elaborat de V. Stefanescu si V. Popa în 1980).

Trusa este confectionata din carton, din piese de aceeasi culoare pe care se deseneaza un disc, un triunghi sau un patrar. Rigletele pot fi confectionate din carton colorat de catre elevi sub supravegherea învatatorului. O astfel de trusa, de dimensiuni mai mici, poate fi folosita de fiecare elev, iar de învatator pentru demonstratii frontale, se realizeaza o trusa de dimensiuni ,mai mari (atât riglete cât si panoul cu liniatura).

Astfel unitatile vor fi reprezentate prin discuri, zecile prin triunghiuri si sutele prin patrate. Panoul pe care vor fi puse rigletele va avea urmatoarea liniatura:

Clasa miilor			Clasa unitatilor
Sute de mii	Zeci de mii	Unitati de mii	Sute	Zeci	Unitati

Pentru clasa I, cartonul suport cu liniatura poate fi marcat numai cu clasa unitatilor, la clasa a II-a cu clasele unitatilor si a miilor, iar la celelalte clase III-IV cu clasele milioanelor si miliardelor.

Folosirea acestei truse este foarte eficienta. Cu ajutorul ei se poate forma orice numar natural. De ex. Pentru numarul 57 panoul va arata în felul urmator

Clasa miilor			Clasa unitatilor
Sute de mii	Zeci de mii	Unitati de mii	Sute	Zeci	Unitati

Pentru adunarea numerelor naturale, ex. 14+23, se formeaza pe cartonul suport cele doua numere, pentru 14 se aseaza rigleta cu 14 discuri pe coloana unitatilor si rigleta cu un triunghi pe coloana zecilor. Lor li se adauga pe coloana unitatilor o rigleta cu trei discuri , iar pe coloana zecilor o rigleta cu doua triunghiuri (de la numarul 23). Numarul obtinut, adica rezultatul adunarii lui 14 cu 23 este 37.

Pentru întelegerea si însusirea scaderii numerelor mai mici decât 20trebuie sa se consolideze cunostintele anterioare ale elevilor cu privire la:

-numerele naturale de la 0 la 20 (formare, numarare, citire, scriere, relatie de ordine)

-adunarea si scaderea numerelor naturale în concentrul 0-10

-compunerea si descompunerea numerelor naturale mai mici decât 10 în doua sau mai multe numere naturale

-zecea ca noua unitati de numarare

-adunarea a doua sau mai multe numere naturale fara si cu trecere peste ordin

-reamintirea si utilizarea expresiilor "marind cu", "micsorând cu", "mai mult cu", "mai putin cu".

La scaderea dintr-un numar format din zeci si unitati, a unui numar format numai din unitati se deosebesc doua cazuri:

-unitatile scazatorului sunt mai putine decât unitatile descazutului - scadere care nu prezinta dificultati nici în predare, nici în întelegerea si însusirea de catre elevi. Se poate începe cu adaugarea si scaderea dintr-un numar de doua cifre a unei unitati, a doua unitati etc.

La scaderea de tipul 15-3 si 16-4, se arata ca întrucât numarul unitatilor descazutului este mai mare cel al unitatilor scazatorului se scad unitatile scazatorului din cele ale descazutului.

Se foloseste descompunerea unui numar într-o zece si numarul unitatilor si proprietatea de asociere.

-unitatile scazatorului sunt mai multe decât cele ale descazutului. De ex. :12-4, 15-7, 14-8 etc.

Avînd în vedere dificultatile pe care le prezinta întelegerea acestui caz în predare, trebuie sa se procedeze cu foarte mare grija, mai ales ca de constientizarea modului în care se rationeaza în aceasta situatie depinde întelegerea cazurilor de trecere peste ordin cu numere mai mari în clasele a II+a si a III-a. Acest caz de scadere se poate explica prin mai multe procedee. De ex. La scaderea 12-5 se poate proceda în felul urmator:

a). Numaram descrescator începând de la 12, cinci numere

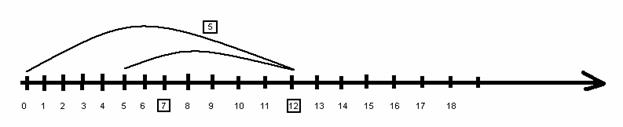
b). Calculam observând desenul

c). Descompunem descazutul sau scazatorul:

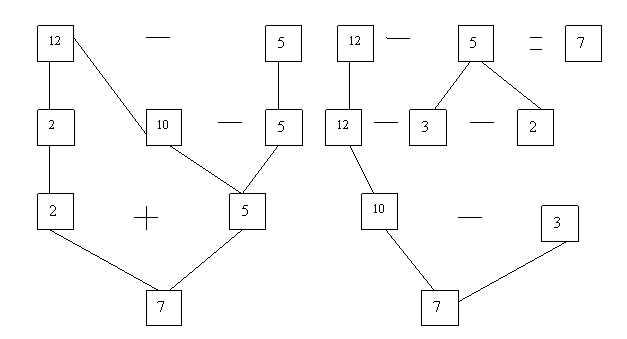
d). Asezarea numerelor unele sub altele:

Z U

Este foarte important ca operatia de scadere sa se însuseasca folosindu-se cunostintele despre adunare. Deasemeni este important sa se utilizeze terminologia specifica (termen, suma, descazut, scazator, rest sau diferenta) si utilizarea legaturii dintre adunare si scadere. Pentru aceasta este foarte important ca elevii sa fie obisnuiti sa verifice, sa faca proba unei adunari sau scaderi prin adunare sau scadere.

III.1.2. Probleme specifice predarii-învatarii adunarii si scaderii numerelor naturale pâna la 100 cu si fara trece peste ordin

Predarea adunarii si scaderii numerelor formate dintr-un numar întreg de zeci se realizeaza insistând asupra faptului ca zecea este o unitate de numarare si ca operatiile de adunare si scadere se realizeaza dupa modelul efectuarilor cu unutati.

De la 1+1=2 se trece la 10+10=20; de la 2+3=5 se trece la 20+30=50; de la 4-2=20la 40-20=20; de la 5-3=2 la 50-20=30.

Realizarea operatiilor se face prin demonstratii frontale si cu ajutorul materialului didactic . Materialul didactic care se foloseste în acest caz poate fi :

betisoare legate în manunchiuri de câte zece;

riglete de câte zece unitati ;

tabla cu piese magnetice pe care se va opera cu simbolul zeci ; triunghiul , iar pentru 10 zeci (o suta ) se va folosi simbolul sutei un patrat ;

trusa cu riglete ;

Cunoasterea primei sute - formarea, citirea si scrierea numerelor , relatia de ordine pe aceasta multime de numere a operatiilor de adunare , scadere ca si de înmultire si de împartire, - constituie baza pentru învatarea întregului curs al aritmeticii si de aceea trebuie ca învatatorul si elevii sa-i acorde o atentie deosebita.

Pentru a se preda adunarea numerelor formate din zeci se pot folosi diverse procedee .

De exemplu operatia 20+10 se poate rezolva în mai multe moduri ● folosirea tablei magnetice :

● folosirea trusei cu riglete:

Clasa unitatilor

SUTE

ZECI

UNITĂŢI

●asezarea unele sub altele a celor doua numere :

Y U

Predare-învatarea adunarii numerelor naturale mai mici decât 100, fara trecere peste ordin, se realizeaza în mai multe etape:

adunarea unui numar format din 4 zeci si unitaticu un numar format numai din unitati ;

adunarea unui numar format din zeci si unitati cu un numar format numai din zeci ;

adunarea a doua numere formate din zeci si unitati

Pentru adunarea unui numar format din zeci si unitati cu un numar format numai din unitati , fara trecere peste ordin , se foloseste descompunerea numarului în zeci si unitati si proprietatile de comutativitate si asociativitate a adunarii.

Pentru a aduna un numar format din zeci si unitati cu unul format numai din zeci se procedeaza astfel :

Exemplu 46+30

Pentru a se aduna doua numere naturale formate din zeci si unitati se poate proceda astfel :

se descompun fiecare din cele doua numere în zeci si unitati ;

folosind proprietatile de comutativitate si de asociativitate ale adunarii, se grupeaza numerele formate numai din zeci si se aduna asemanator si cele formate numai din unitati ;

se aduna sumele partiale :

exemplu 35+42=(30+5)+(40+2)

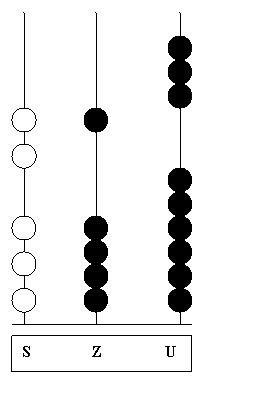
Adunarea numerelor naturale cu trecere peste ordin se învata trecând prin mai multe etape. Toate procedeele se bazeaza pe formarea si scrierea zecimala a numerelor naturale si faptul ca zece unitati de ordinul I formeaza o unitate de ordinul II, zece unitati de ordin II formeaza o unitate de ordin III s.a.m.d. pentru numerele mai mari decât 1000.

Este foarte important ca la aceste exercitii paralel cu calculul oral sa se efectueze si calculul în scris.

Exemplu :

a). Adunarea cu trecere peste ordinul unitatilor

S	Z	U

S Z U

b) adunarea cu trecere peste ordinul zecilor;

S	Z	U

scaderea cu trecere peste ordin a numerelor naturale de la 0 la 1000.

S	Z	U



Transformam o zece în zece unitati

5 sute - 1 suta =4sute

3 zeci si 2 zeci = 1 zeci

Verificam!

În functie de nivelele de pregatire ale elevilor , de posibilitatile intelectuale si de experienta lor si a învatatorului se pot aplica aceste procedee sau altele.

O situatie aparte o reprezinta scaderile în care cifrele de un anumit ordin fie ale descazutului, fie ale scazatorului, sunt 0 .Întelegerea si însusirea de catre elevi a acestui tip de scadere se va face prin multe exercitii si cu exemple cât mai variate .

La scaderile în care la descazut atât la cifra unitatilor cât si la cea a zecilor sunt 0 , elevii sesizeaza mai greu câ se ia o suta de la sutele descazutului si se transforma în 10 zeci si ca din acestea se ia o zece si se transforma în unitati .

La început la calculul înscris pe verticala este bine sa se evidentieze si sa consemneze aceste lucruri .

III.1.4. Probleme specifice predarii-învatarii adunarii si scaderii numerelor naturale mai mari decât 1000.

Operatiile de adunare si de scadere a numerelor naturale mai mari decât 1000 se efectueaza oral si în scris în etape similare si prin peocede asemanatoare cu cele învatate la adunarea si scaderea numerelor naturale mai mici decat 1000.

Pentru adunarea cât si pentru scaderea numerelor naturale mai mari decât 1000 este necesar sa fie cunoscute temeinic de catre elevi clasele si ordinele în scrierea zecimala a acestor numere, ordinea claselor si ordinea ordinilor în fiecare clasa, scrierea si citirea corecta a numerelor de orice marime, operatii de adunare si de scadere însusite anterior. Prin exercitii repetate, trecându-se prin etape similare cu cele prin care s-a trecut la efectuarea acestor operatii cu numere mai mici, comparativ se va ajunge la concluzia ca tehnica de calcul este aceeasi.

Exemple :

M S Z U

Verificarea rezultatului

1243+2135=3378 proba 2135+

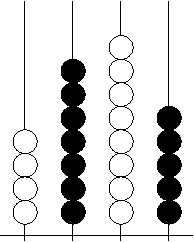
M S Z U

Se descompun numerele: (4000+700+80+5)- 4785

Verificarea rezulttului:

-prin scadere -prin adunare

Se aplica regula învatata: transferam 10 unitati de un anumit ordin într-o unitate de ordin superior.

Verificari

-prin scadere -prin adunare

III.2. Modalitati de preare -învatare a operatiilor de înmultire si împartire a numerelor naturale.

III.2.1. Înmultirea si împartirea numerelor naturale de la 1 la 10

Operatiile de înmultire si împartire se introduc la clasa a III-a, dupa ce elevii au dobândit cunostinte si au format priceperi si deprinderi de calcul privitoare la operatiile de adunare si scadere a numerelor naturale.

Conform programei scolare în vigoare, aceste operatii se predau separat. În predarea înmultirii este esentiala evidentierea legaturii cu adunarea (repetata), iar în predarea împartirii este importamta evidentierea scaderii repetate.

Dupa ce a fost introdusa operatia de împartire (în parti egale si prin cuprindere). În stabilirea tablei împartirii este bine sa se foloseasca tabla înmultirii, legatura ce exista între împartire si înmultire.

Îm predarea si învatarea operatiei de înmultire, intuitia nu mai are un rol predominant, (ca la adunare) deoarece elevii au dobândit cunostinte si si-au format priceperi si deprinderi în legatura cu operatia de adunare.

La început, se vor reactualiza cunostiintele despre adunare, insistându-se pe adunarea repetata, (adunarea mai multor termeni egali), proprietatile de comutativitate si asociativitate ale adunarii, modul de formare, scriere si citirea numerelor naturale.

Exemplu :

De 4 ori câte doua baloane se pot scrie :

x2=2+2+2+2=8

4 este numarul care arata de câte ori se repeta 2

2 este numarul care se repeta

X este semnul operatiei de înmiltire

4x2=8 se citeste

4 înmultit cu 2 este egal cu 8 sau

4 ori 2 este egal cu 8

4 x 2 = 8

Se spune copiilor ca pentru adunarile repetate se mai foloseste si o alta scriere.

Desi rolul mijloacelor intuitive în introducerea înmultirii nu mai este preponderent, pentru ca elevii sa înteleaga înmultirea ca adunare repetata, învatatorul nu trebuie sa renunte complet la ele.

De 3 ori câte 4

3 x 4 =4+4+4=12

Mai pune câte unul în fiecare farfurie si mai ramân 6-3=3

Mai pune câte unul în fiecare farfurie si mai ramân 3-3=0

Se concluzioneaza ca 12 împartit în mod egal la 3 sau 12 împartit la 3 este egal cu 4.

Acest lucru se scrie 12 : 3 = 4. simbolul operatiei de împartire este " : " si se citeste împartit. Numarul care se împarte se numeste deîmpartit, iar cel la care se împarte se numeste împartitor.

La început este bine ca învatatorul sa foloseasca material didactic variat si apropiat experientelor de viata (creioane, bile, betisoare, nuci, mere, caiete, e.t.c.).

Analizând modul în care se face împartirea, vedem ca se efectueaza scaderea partilor egale, prin scaderi repetate din numarul initial, apoi din primul rest, în continuare din al II.lea rest s.a.m.d. . De exemplu pentru a împarti 12 la 3 efectuam 4 scaderi: 12-3=9, 9-3=6, 6-3=3, 3-3=0. numarul de scaderi efectuate este câtul împartirii

Scaderea repetata se foloseste numai la început când se introduce operatia de împartire , când se pune în evidenta , cu ajutorul materialului intuitive, semnificatia acestei operatii .Pe masura ce se formeaza notiunea de împartire ca scadere repetata, se va folosi legatura ei cu înmultirea , scotându-se în evidenta faptul ca rezultatele ei se gasesc repede folosind tabla înmultirii.

De exemplu : 12 x 3 = 4 deoarece 4 x 3 = 12 sau 15:3=5 deoarece 3 x 5 = 15

Împartirea prin cuprindere se bazeaza pe separarea unei multimi în submultimi disjuncte doua câte doua, cu acelasi numar de elmente (echivalente). Cunoscându-se câte elemente are fiecare submultime , prin operatia de înpartire se afla câte submultimi se formeaza .Acest mod de împartire reprezinta un grad mai mare de dificultate , întrucât nu se poate ilustra în mod concret si atât de usor ca la împartirea în parti egale .

La problemele la care se impune folosirea procedeului de împartire prin cuprindere se stabileste numarul de obiecte ce trebuie împartit. De exemplu: 12 creioane , câte 3 la fiecare elev, câti elevi primesc creioane? Se scad 3 creioane , apoi altele 3 pâna nu mai ramâne nici un creion .Se numara câte scaderi sau efectuat : 12 - 3 = 9, 9 - 3 = 6, 6 - 3 = 3, 3- 3 = 0. Numarul scaderilor efectuate este câtul împartirii la 12 . Deci 12 : 3 = 4, adica 4 elevi primesc creioane .

Atât la împartirea în parti egale cât si la înpartirea prin cuprindere, pentru a efectua împartiri se fac scaderi repetate .

Pentru cunoasterea , fixarea si aplicarea tablelor înmultirii si împartirii trebuie efectuat un numar mare de exercitii si probleme, a caror rezolvare se face aplicând aceste table în diferite situatii.În felul acesta elevii vor reusi sa recunoasca situatiile matematice si practice în care se impune efectuarea înmultirilor si împartirilor .

Pentru cunoasterea , fixarea si aplicarea tablelor înmultirii si împartirii trebuie efectuat un numar mare de exercitii si probleme, a caror rezolvare se face aplicând aceste table în diferite situatii. În acest fel elevii vor reusi sa recunoasca situatiile matematice si practice în care se impune efectuarea înmultirii si împartirii.

Prin exercitii si rezolvari de problemese vor scoate în evidenta si se vor însusi procedeele de realizare a probei împartirilor, prin înmultirea câtului cu împartitorul se vor obtine deîmpartitul sau prin împartirea deîmpartitului la cât pentru a se obtine împartitorul .

Predarea-învatarea înmultirii si a împartirii cu numere formate din mai multe cifre

Înmultirea si împartirea dintre numerele formate din mai multe cifre se bazeaza pe proprietatile de scriere în baza zece a numerelor naturale, pe proprietatile operatiilor de adunare si înmultire a numerelor naturale (asociativitate, comutativitate, distributivitatea înmultirii fata de adunare si scadere), simetria relatiei de egalitate, pe procedeele de calcul învatate, pe folosirea probelor operatiilor .

III.2.Înmultirea numerelor formate din mai multe cifre

Dupa ce prin exercitii si rezolvari de probleme se introduc si se însusesc de catre elevi proprietati de asociativitate, comutativitate ale operatiei de înmultire si distributivitatea înmultirii fata de adunare, se trece la predarea înmultirii cu 10 si cu 100 a numerelor panala 10 , apoi la înmultirea cu 10 a numerelor formate din zeci si unitati . Aceste reguli de calcul se vor utiliza si mai târziu la înmultirea numerelor de mai multe cifre.

Exercitiile din aceasta actegorie se grupeaza dupa gradul de dificultate:

a)Înmultirea unui numar natural de doua cifre cu un numar natural de o cifra,

calculul se bazeaza atât pe descompunerea numarului format din doua cifre în zeci si unitati cât si pe aplicarea proprietatii de distributivitate a înmultirii fata de adunare .

Exemplu :2 x 34 = 2 x (30 +4) = 2 x 30 + 2 x 4 = 60 + 8 = 68

Deducerea regulii de calcul scris se bazeaza pe faptul ca înmultirea este o adunare repetata si pe posibilitatea de înlocuire a adunarii repetate prin înmultire .

34 + 34 x

Se înmulteste cifra untatilor cu 2:2x4=8

Se înmulteste cifra zecilor cu 2 : 2 x 3 =6

Înmultirea cu trecere peste ordin se bazeaza pe procedeele (regulile) învatate anterior si aplicarea reguli ca zece unitati de un anumit ordin , formeaza, o unitate de ordin imediat urmator.

Exemplu :

3 x 29 = ?

3 x 29 = 3 x ( 20 + 9 ) = 3 x 20 + 3 x 9 = 60 + 27 = 87

29 x

Se înmulteste cu 3 cifra unitatilor si se obtine 3 x 9 = 27 de unitati sau 2 zeci si 7 unitati .Se scrie 7 pe locul unitatilor, iar zecile se vor aduna cu produsul obtinut de înmultirea zecilor.

Se înmulteste 3 cu cifra zecilor 3 x 2 = 6 ; 6 + 2 = 8

Înmultirea cu trecere peste ordinul unitatilor si al zecilor .

254 x 3 = (200+50+4) x 3

= 200x3 +50x3 + 4 x3

254 x

Se înmulteste 3 cu cifra unitatilor 3 x 4 = 12 Sa o zece si doua unitati , zecea se va aduna cu produsul obtinut dupa înmultirea zecilor.

Se înmulteste 3 cu cifra zecilor 3 x 5 = 15 15 + 1 = 16 , 16 zeci o suta sase zeci. Suta se va aduna cu produsul obtinut dupa înmultirea sutelor.

b) Înmultirea cu numere formate din doua , trei sau mai multe cifre

printre elementele de tehnica a acestor înmultiri se numara si acela de asezare a factorilor, în mod special a celor care se termina în zerouri.

Aceste zerouri nu se înmultesc, dar se adauga la produsul total. Fiecare unitate a numarului cu care înmultim se înmulteste succesiv, cu toate unitatile de orice ordin a numarului pe care îl înmultim. Din înmultirea fiecarei unitati de ordin se obtine un produs partial. Scrierea produselor partiale este esentiala , ea începând de la dreapte la stânga si cu ordinul pe care se înmulteste, înmultirea începe cu cifra unitatilor , numarul cu care înmultim. Prin adunare produselor partiale se obtine produsul celor doua numere pe care le înmultim .

Exemple : 1) 24 x 20 = ?

24 x 20 = 24 x(2 x 10)

=(24 x 2) x 10

= 48 x 10

24 x

Nu se înmulteste cu 0 pentru ca se obtine produsul, dar se coboara la 0 la produs.

24 x 35 = 24 x ( 30 + 5 )

=42 x 30 + 24 x 5

24 x

120 primul produs partial Se înmulteste cifra unitatilor

72 de la al II-lea factor cu primul factor.

Grupeaza câte 5 flori .

A obtinut trei grupe si au ramas doua flori .

a). Deîmpartitul este scris cu doua cifre. Ca punct de plecare se poate folosi urmatoarea problema:

La un magazin s-au adus 64 kg de zahar si 56 kg de faina. Pentru a le pune în vânzare se ambaleaza în pungi de 2 kg. Câte pungi cu zahar s-au ambalat? Dar cu faina?

6 se împarte cifra zecilor

= se împarte cifra unitatilor

4 se împarte cifra zecilor 5:2

16 câtul 2 restul 1, 5=2x2+1

== se împart unitatile ramase o zece=10 unitati

b). Deîmpartitul este scris cu trei cifre

Pentru serbare s-au cumparat 369 de baloane. Pentru câti copii ajung baloanele daca fiecare a primit câte 3 baloane?

se împart sutele

se împart zecile

9 se împart unitatile

c). Alte cazuri de împartire: 406:2=?

Pentru simplificarea calculului se scrie : 406:2=203

Observam ca numarul sutelor este mai micdecât împartitorul: 3:6 da câtul 0 si restul 6. se considera primele doua cifre si se efectueaza împartirea, respectând regulile învatate.

Cum calculam?

30 6 se cuprinde în 35 de 5 ori

54 5 x 6 =30

54 zecile ramase se transforma în unitati 6 se cuprinde în 54 de 9 ori 9x6=54

Elevii vor întelege ca sutele se transforma în zeci si se aduna cu zecile apoi se efectueaza împartirea.

IV. Aspecte metodice privind predarea-învatarea numerelor rationale si a operatiilor aritmetice cu ele.

Programa de matematica privind clasa a III-a prevede însusirea notiunilor de jumatate si sfert, paralel cu învatarea împartirii prin 2 si respectiv 4.

În prima lectie elevii învata împartirea prin 2 si înteleg semnificatia acestei operatii (de micsorare de 2 ori) iar în a II-a lectie îsi însusesc notiunea de jumatate (fara a folosi obligatoriu termenul de doime si fara a introduce , scrie si citi fractia . Este important sa înselegem si sa stim cum va proceda învatatorul an clasa :

-Învatatorul si elevii vor avea asupra lor materialul didactic intuitivconcret necesar, cum ar fi : betisoare riglete figuri geometrice decupate (dreptunghi, cerc), creioane colorate s.a.m.d. Folosind strategii didactice de genul explicatiei, demonstratiei, conversatiei euristice, descoperirii, problematizarii si lucrând frontal sau independent, lectia(în secvente esentiale) decurge astfel:

- Se taie de câtre învatator un mar în jumatate . (Ce am facut? Câte parti am obtinut? Cum sunt ele? Daca înlaturam cele doua parti ce obtinem ? Ca sa obtinem o jumatate de mar ce putem face ? Voi ati putea realiza?Cine încearca?)

- Se continua cu împartirea (prin îndoire si taiere) în doua parti egale a imaginii unui cerc, decupate din hârtie. Se pot folosi întrebari constatative, de demonstrare si descoperire analoage cu cele de mai înainte. Din aceste secvente, elevii vor începe sa înteleaga ca pentru a obtine o jumatate dintr-un întreg (obiect) trebuie sa-l împartim în doua parti egale .

- Învatatorul poate continua : Daca avem un cerc desenat cum putem obtine o jumatate din el ? (se va face apel la experienta de îndoire). Se va trasa pe imaginea cercului o linie care sa-l împarta în doua parti egale si se va hasura (coloana) una dintre ele pentru a se scoate în evidenta jumatatea. Activitate similara vor efectua apoi si elevii. Se va accentua înca o data ca pentru a obtine o jumatate dintr-un cerc se împarte cercul în doua parti egale. Asemanator se va proceda cu un dreptunghi.

. În continuare elevii vor fi solicitati sa desparta multimea de betisoare pe care o au (formata din 6-8 betisoare în doua submutimi care sa aiba fiecare acelasi numar de betisoare); analog cu multimile de jetoane. Se va scoate în evidenta ca pentru a obtine dintr-o multime o submultimecare sa aiba jumatate din numarul de elemente date se împarte numarul de elemente ale multimii date la 2.

. se poate continua cu rezolvarea unei probleme simple (Ionel are 10 garoafe. Jumatate din numarul lor le ofera doamnei învatatoare, iar restul le va da mamei sale. Câte garoafe va oferi Ionel mamei sale?). se vor compune si rezolva înca 1-2 probleme asemanatoare.

Explicându-se si reamintindu-se ca ceea ce s-a obtinut prin taierea sau sectionarea unui numar sau cerc în doua parti egale, prin formarea din elementele unei submultimi a doua submutimi cu atâtea elemente fiecare cât se obtin prin împartirea numarului elementelor cu jumatate din numarul elementelor unei multimi date, învatatorul generalizeaza: pentru a obtine jumatatea unui mar se împarte acest numar la 2.

Pentru însusirea sfertului sau a patrimii, dupa însusirea împartirii cu 4 , se poate proceda asemanator.

În clasa a IV-a studiul numerelor rationale va începe cu repetarea notiunilor de jumatate-doime si sfert-patrime.

Programa scolara prevede introducerea notiunilor de unitate fractionara, de doime si de patrime si simbolurile grafice corespunzatoare. Se va continua apoi cu introducerea unitatii fractionare treimea, sesimea, optimea. si simbolurile grafice respective etc.

Se va scoate în evidenta de fiecare data ca:

a) o unitate fractionara este o parte din numarul de parti egale în care s-a împartit un obiect, un numar;

b) o unitate fractionara este egala sau nu cu o alta unitate fractionara daca numarul de parti egale în care am împartit întregul este acelasi sau nu. Se vor face aplicatii constând în exercitii de compunere a întregilor din mai multe unitati fractionare, se vor rezolva si compune probleme cu acestea.

si în clasa a IV-a la predarea -îvatarea unitatii fractionare se va folosi un bogat si sugestiv material intuitive, se vor utilize metode si procedee didactice de naturasa-I incite pe elevi, sa activizeze conduita intelectuala a acestora. Totodata, se vor folosi procedee de evaluare care sa surprinda progresele facute în planul operationalitatii specifice gândirii matematice.

Concomitant cu introducerea unitatii fractionare si a simbolului sau graphic format din doua numere suprapuse despartite printr-o linie, se va explica si defini elevilor ca: numarul de sub linie poarta denumirea de numitor si arata în câte parti egale am împartit întregul, linia dintre numere se numeste linie de fractie si ca numarul de deasupra liniei de fractie se numeste numarator si arata ca din numarul de parti egale în care am împartit întregul s-a luat doar o singura parte.

Dupa însusirea corecta a notiunii de unitate fractionara, trecând prin aceleasi etape, se introduce numerele rationale. Cum vom proceda? Taind un mar în patru parti egale se obtin 4 sferturi sau 4 patrimi de mar. Daca alaturam doua din ele obtinem 2 patrimi de mar si exprimam acest lucru în scris prin simbolul 2/4. urmeaza un set de întrebari: daca mai alaturam înca un sfert de mar cate sferturi de mar vom avea? Prin ce fractie vom exprima 3 patrimi? Cât este numitorul acestei fractii s ice reprezinta el? Cât este numaratorul s ice semnifica? Cum putem sa citim pe ¾ (3 pe 4, 3 supra 4, 3 patrimi din 4 parti egale, 3 sferturi, 3 patrimi)/

Daca alaturam 2 sferturi la alte 2 sferturi ce obtinem? La trei sferturi câte sferturi putem adauga ca sa obtinem întregul? O jumatate din câte sferturi este formata? Dar 2 jumatati? Raspunsurile se pot da oral, fie printr-o aplicatie practica, fie prin desen sau prin toate procedeele la un loc.

În continuare se vor face exercitii de citire si scriere de unitati fractionare si de fractii, se va realiza reprezentare lor pe desen folosind creioane colorate. Intuitive, prin sectionare de obiecte sau figurative, spre exemplu cu ajutorul segmentelor (fig.1), se poate preda-învata compararea fractiilor fata de un întreg sau între ele si se va defini egalitatea dintre fractii. Prin defintie spunem ca doua sau mai multe fractii sunt egale daca fiecare reprezinta aceeasi parte dintr-un întreg.

În desenul urmator (fig.2) se observa ca din segment reprezinta cât din acelasi segment sau cât din el. Deci

din cerc), sau 2 sferturi ( din cerc) reprezinta fiecare aceeasi parte din cerc, deci toate sunt fractii egale. Prin aplicatii practice, prin observatii si comparatii se poate descoperii si însasi ca si alte fractii sunt echivalente:

Avantajul care îl prezinta acest mod intuitive de introducere a egalitatilor ditre fractii se datoreaza faptului ca el deriva dintr-0 identitate de marimi fizice.

Daca elevii îsi însusesc bine notiunea de egalitate a fractiilor, li poate sugera modalitatea de a obtine dintr-o fractie data prin înmultirea atât a numitorului, cât si a numaratorului (amplificarea fractiei), sau împartirea celor 2 factori (simplificarea fractiilor) cu acelasi numar (în cazul în care se poate face), un numar diferit de 0.

IV.1. Compararea fractiilor

Aceasta se realizeaza în doua sensuri:

compararea unei fractii cu un întreg;

compararea a doua sau mai multe fractii (daca au acelasi numitor sau acelasi numarator) între ele.

Se revine asupra faptului ca un întreg poate fi exprimat printr-o fractie în care numaratorul si numitorul sunt numere egale.

Se definesc fractia echiunitara -ca fiind orice fractie care este egala cu un întreg- si fractia subunitara-ca fiind o fractie în care numarul partilor luate , numaratorul este mai mic decât numarul partilor în care am împartit, numitorul. Se demonstreaza prin aplicatii practice existenta fractiilor în care numaratorul este un numar mai mare decât cel de la numitor (fractii supraunitare). Acest lucru se poate realize prin împartirea a doi sau mai multi întregi- fiecare în acelasi numar de parti egale- si luarea unui numar mai mare de parti decât a fost împartit fiecare întreg (în fig.3 s-au colorat 5/4).

Se poate apela la experienta de viata a copiilor . Spre exemplu, daca elevul se duce la magazin si solicita o pâine si jumatate , vânzatoarea îi da o pâine (2 jumatati) si înca o jumatate din alta paine. Deci, în total, trei jumatati.

(vezi fig. 4). Se poate concluziona ca doimea este cea mai mare unitate fractionara, ca urmeaza treimea, ca între doua unitati fractionare mai mare este aceea care are numitorul mai mic: fiindca 5>8 sau 8>5.

Fig. 6

Se trece în acelasi mod de reprezentare sau concret la compararea fractiilor care au acelasi numitor. Daca împartim un singur cerc în 8 parti de aceeasi marime si coloram 5 dintre ele se poate observa: partea din cerc colorata (5/8 din suprafata cercului) este mai mare decât partea din cerc necolorata (3/8 din suprafata cercului) si vom scrie

Se generalizeaza: dintre doua fractii care au acelasi numitor,mai mare este fractia care are numaratorul maim arte. De exemplu: fiindca 5>1.

În sfârsit, folosind acelasi procedeu figurative se trece la compararea fractiilor care au acelasi numarator, dar numitori diferiti.

Prin observatie, comparatie si analiza se poate generalize: fractia fiindca prima fractie reprezinta mai mult dintr-un întreg decât cea de-a doua fractie. Dupa mai multe exercitii se generalizeaza: dintre doua fractii care au acelasi numarator este mai mare fractia care are numitorul mai mic.

IV.2. Operatii cu fractii care au acelasi numitor

În clasa a IV-a programa scolara prevede numai efectuarea operatiilor de adunare si scadere a numerelor fractionare care au acelasi numitor.

Dificultatîle în însusirea acestor operatii vor fi relative mici, daca elevii au constientizat notiunile de unitate fractionara si de numar rational.

Introducerea operatiei de adunare se poate face prin mai multe modalitati, fiecare având însa un suport intuitive. Elevii trebuie sa înteleaga ca pentru adunarea fractiilor care au acelasi numitor se procedeaza ca si la adunarea numerelor concrete (2 mere + 4 mere = 6 mere), ca se aduna un numar de unitati fractionare cu acelasi numitor , sau 2 septimi adunate cu 3 septimi dau rezultatul a 6 septimi.

Daca se împarte un cerc (prin ducerea a 4 diametre) în 8 parti de aceeasi marime (fig. 7) si se coloreaza cu albastru 2 din cele 8 parti si cu roz alte 4 parti se observa, împreuna cu elevii, ca partea colorata din figura este formata din 6 parti din cele 8 în care am împartit cercul. Deci vom scrie:

Vom spune ca numarul fractionar este suma dintre numerele fractionare si . Se va accentua idea ca numaratorul 6 al sumei este obtinut prin adunarea numaratorilor fractiilor care se aduna. Sau, folosind un desen asemanator (fig. 8), daca din 6 parti colortate scadem 2 parti colorate obtinem 4 parti colorate. Cu ajutorul simbolurilor vom scrie:

În cazul în care învatatorul considera ca nivelul clasei nu permite sa se introduca aceste operatii pe baza de imagini se poate apela la un material concret-intuitiv: împartirea în parti egale a unui mar, portocala etc.. si operarea sub forma de adunare sau scadere cu o parte dintre ele. Tot pe astfel de material, prin observatie si analiza, pot fi orientati elevii sa intuiasca proprietatile adunarii: asociativitatea, comutativitatea, dupa care se trece la generalizarea lor în cazul numerelor rationale.

Asemanator cu adunarea în multimea numerelor naturale, fara trecere si cu trecere peste ordin, trebuie sa se înceapa cu adunarea a doua sau mai multe numere rationale cu acelasi numitor al carui rezultat sa aiba numaratorul mai mic decât numitorul (se va obtine o fractie subunitara); si dupa un numar necesar de exercitii si dupa însusirea corecta si deplina a algoritmului de adunare a acestor numere, se va trece la adunari de numere rationale cu acelasi numitor, ale caror rezultate sa fie fractii echiunitare sau supraunitare.

Deci rezultatul în acest caz este o fractie supraunitara:

Se pot folosi în acest caz materiale intuitive concrete: daca se adauga la 3 sferturi de mar înca 2 sferturi de mar, rezultatul va fi mult mai mult decât un mar întreg, va fi un mar întreg si înca un sfert de mar.

Se va insist ape faptul ca în adunarea sau scaderea fractiilor cu acelasi numitor, numitorii fractiilor nu intervin în calcul, adica ramân neschimbati, adunarea sau scaderea facându-se între numaratori.

Atât adunarea cât si scaderea fractiilor cu acelasi numitor se pot introduce si prin utilizarea unor probleme-actiuni simple si semnificative din viata practica a elevilor.

Dupa cunoasterea modului de efectuare a operatiilor de adunare si scadere, se fac si exercitii în care sa apara si ambele operatii:

Învatatorul trebuie sa insiste asupra procesului de formare a deprinderii de scriere corecta a fractiilor în succesiunea lor în cadrul exercitiilor: scrierea semnului operatiei (+ sau -) în dreptul liniei de fractie a primului termen, iar dupa semn, pe aceeasi linie se va trasa mai întâi linia de fractie a urmatorului termen si apoi se va scrie numitorul si numaratorul sau.

Totodata, în functie de nivelul cunostintelor elevilor, de ritmul parcurgerii programei si în accord cu necesitatile de individualizare si diferentiere a activitatilor didactice, se realizeaza si sarcini de genul:

a) scrierea fractiilor supraunitare sub forma de fractii mixte;

b) transformarea unei fractii supraunitare în fractie mixta si invers;

c) efectuarea de adunari si scaderi între numerele rationale si întregi

d) ordonarea pe axa numerica a numerelor rationale; raportarea lor fata de numerele naturale;

e) rezolvarea unui numar însemnat de probleme în care datele si solutia sa fie numere rationale.

IV.3. Aflarea unei fractii dintr-un întreg

Unul dintre obiectivele urmarite prin predarea fractiilor în clasa a IV-a constituie aflarea unei fractii dintr-un numar.

Procesul de calculare al liniei de fractie dintr-un întreg parcurge 2 etape distincte:

a) calcularea unei singure unitati fractionare dintr-un întreg (un numar natural), adica aflarea unei parti dintr-un întreg;

b) calcularea unei fractii oarecare dintr-un întreg, adica aflarea mai multor parti la fel de mari dintr-un întreg.

Pentru prima categorie de exercitii se procedeaza intuitiv, folosind mai întâi figure geometrice decupate, figure geometrice desenate, apoi cantitati, lungimi, mase, volume, etc., ajungându-se la numere. De exemplu:

-sa se afle ¼ din aria unei suprafete dreptunghiulare;

-sa se afle 1/3 din 18 kg., 60 kg., 84 kg.;

-sa se afle ½ din 22L, 40L, 52L,..;

-sa se afle ¼ din numerele 8, 24, 32, 40,...;

Operatiile se vor scrie astfel:

-din 18kg. reprezinta 18:3=6;

-din 22L reprezinta 22:2=11;

-din 8 reprezinta 8:4=2.

Utilizand mai multe exemple asemanatoare si facand analiza lor, vom stabili atât operatia, cât si procedeul de aflare a unei singure unitati fractionare dintr-o marime sau numar.

Pentru a II-a categorie de exercitii sunt necesare 2 operatii:

-împartirea pentru aflarea unei singure unitati fractionare de felul celei pe care îl arata numitorul;

- înmultirea pentru aflarea numarului de unitati fractionare pe care îl arata numaratorul.

V. Jocul didactic si activitatile matematice

Jocul reprezinta un ansamblu de actiuni si operatii care, paralele cu destinderea, buna dispozitie si bucuria, urmareste obiective de pregatire intelectuala, tehnica, morala, fizica a copilului.

Încorporat în activitatea didactica, elemental de joc imprima acesteia un caracter mai viu si mai atragator, aduce varietate si o stare buna de dispozitie functionala, de veselie si de bucurie, de divertisment si de destindere, ceea ce previne aparitia monotoniei si a plictiselii, a oboselii. Restabilind un echilibru în activitatea scolarilor, jocul fortifica energiile intelectuale si fizice ale elevilor, generând o motivatie secundara, dar stimulatory, constituind o prezenta indispensabila în ritmul accentuat al muncii scolare.

Jocul didactic este un tip specific de activitate prin care învatatorul consolideaza, precizeaza si chiar verifica cunostiintele elevilor, le îmbogateste sfera lor de cunostiinte, pune în valoare si le antreneaza capacitatile creatoare ale acestora.

Asadar, atunci când jocul este utilizat în procesul de învatamânt, el dobandeste functii psihopedagogice semnificative, asigurând participarea activa a elevului la lectie, sporind interesul de cunoastere fata de continutul lectiei.

O data cu împlinirea vârstei de 6 ani, în viata copilului începe procesul de integrare în viata scolara, ca o necessitate obiectiva determinata de cerintele instruirii si dezvoltarii sale multilaterale. De la aceasta vârsta, o buna parte din timp este rezervata scolii si activitatii de învatare care devine o preocupare majora. În programul zilnic al elevului intervin schimbari impuse de ponderea pe care o are acum scoala, schimbari care nu diminueaza însa dorinta lui de joc, jocul ramânând o problema majora în timpul întregii copilarii.

În aceste conditii, se impune o exigenta sporita în ceea ce priveste dozarea ritmica a volumului de cunostiinte matematice ce trebuie assimilate de elev si în mod deosebitnecesitatea ca lectia de matematica sa fie completata sau intercalata cu jocuri didactice cu continut mathematic.

Un exercitiu sau o problema de matematica poate deveni joc didactic mathematic daca:

-realizeaza un scop si o sarcina didactica din punct de vedere matematic;

-foloseste elemente de joc în vederea realizarii sarcinii propuse;

-foloseste un continut matematic accesibil si atractiv;

-utilizeaza reguli de joc, cunoscute anticipat si respectate de elevi.

a) scopul didactic se formuleaza în legatura cu cerintele programei scolare pentru clasa respectiva, convertite în finalitati functionale de joc. Formularea trebuie sa fie clara si sa oglindeasca problemele specifice impuse de realizarea jocului respectiv. O formulare corespunzatoare a scopului determina o buna orientare, organizare si desfasurare a activitatii respective.

b) sarcina didactica

Sarcina jocului didactic matematic este legata de continutul acestuia, de structura lui, referindu-se la ceea ce trebuie sa faca în mod concret elevii în cursul jocului, pentru a se realiza scopul propus. Sarcina didactica reprezinta esenta activitatii respective, antrenand intens operatiile gândirii: analiza, sinteza, comparatia, dar si ale imaginatiei. Jocul didactic matematic cuprinde si rezolva cu success, de regula, o singura sarcina didactica, în concluzie, sarcina didactica constituie elementul de baza prin care se transpune , la nivelul elevilor, scopul urmarit în activitatea respectiva. Spre exemplu, în jocul didactic "Cauta vecinii" scopul didactic este consolidarea deprinderilor de comparare a unor numere, iar sarcina didactica sa gaseasca numarul mai mare sau mai mic cu o unitate decat numarul dat; în jocul "Cine urca scara mai repede" scopul este consolidarea deprinderilor de calcul cu cele 4 operatii, iar sarcina didactica este efectuarea unor exercitii de adunare ,scadere, înmultire si împartire.

c) elemente de joc

În jocurile didactice matematice se pot alege cele mai variate elemente de joc: întrecere (emulatie/competitie) individuala sau pe grupe de elevi, cooperarea între participanti, recompensarea rezultatelor bune sau penalizarea greselilor comise de catre cei antrenati în jocurile de rezolvare a exercitiilor sau a problemelor, bazate pe surpriza, asteptare, aplauze, cuvantul stimulator etc.. O parte din aceste elemente se utilizeaza în majoritatea jocurilor didactice , altele, în functie de continutul jocului. Important este ca elementele de joc sa se împleteasca strans cu sarcina didactica, sa mijloceasca realizarea ei în cele mai bune conditii.

d) continutul matematic al jocului didactic trebuie sa fie accesibil, recreativ si atractiv prin forma în care se desfasoara, pri mijloacele de învatamânt utilizate, prin volumul de cunostiinte la care se apeleaza.

e) materialul didactic:

reusita jocului didactic matematic depinde în mare masura de materialul didactic folosit, de alegera corespunzatoare si de calitatea acestuia.

Materialul didactic trebuie sa fie variat, cât mai adecvat continutului jocului , sa slujeasca cât mai bine scopul urmarit. Astfel se pot folosi: planse, folii, fise individuale, cartonase, jetoane, trusa cu figure geometrice.

f) regulile jocului.

Pentru realizarea sarcinii propuse si pentru stabilirea rezultatelor întrecerii se folosesc reguli de joc propuse de învatator sau cunoscute în general de elevi. Aceste reguli concretizeaza sarcina didactica si realizeaza, în acelasi timp, sudura între aceasta si actiunea jocului. Regulile de joc transforma defapt exercitiul sau problema de joc, activizând întregul colectiv de elevi la rezolvarea sarcinilor primate. Exista si jocuri în care elevii sunt antrenati pe rând la rezolvarea sarcinilor didactice. În aceste jocuri este recomandabil ca propunatorul sa introduca o completare la regula, în sensul de a cere grupei sa-l urmareasca pe cel întrebat si sa raspunda în locul lui, daca este cazul.

În cazul "Cine urca scara mai repede?" regula cere elevilor sa completeze pe planse\pe tabla, rezultatul , iesind castigatoare echipa care va reusi sa resolve correct si rapid exercitiile, adica cea care va ajunge mai repede în varf.

Asadar, jocurile didactice matematice cuprind unele reguli care precizeaza cine poate deveni câstigatorul jocului. În acelasi timp ele cuprind si unele restrictii: elevii care nu reusesc, vor fi scosi din joc sau vor fi penalizati, depunctati.

Prin folosirea jocurilor didactice în predarea matematicii la clasele mici se realizeaza importante sarcini formative ale procesului de învatamânt. Astfel jocurile didactice matematice :

antreneaza operatiile gandirii: analiza, sinteza, comparatia, clasificarea, ordonarea, abstractizarea, generalizarea, concretizarea.

Dezvolta spiritual de initiativa si independenta în munca, precum si spiritual de echipa;

Dezvolta spiritual imaginativ-creator si de observatie;

Dezvolta atentia , disciplina si spiritual de ordine în desfasurarea unei activitati;

Formeaza deprinderi de lucru correct si rapid;

- Asigura însusirea mai rapida , mai temeinica, mai accesibila si mai placuta a unor cunostiinte relative aride pentru acesta vârsta (numeratia, operatiile aritmetice etc.).

Reusita jocului didiactic este conditionata de proiectarea, oragnizarea si desfasurarea lui metodica, de modul în care învatatorul stie sa asigure o concordanta deplina întra toate elementelece-l definesc.

Pentru aceasta, învatatorul va avea în vedere urmatoarele cerinte de baza:

pregatirea jocului didactic;

organizarea judicioasa a acestuia;

respectarea momentelor jocului didactic;

ritmul si strategia conducerii lui;

stimularea elevilor în vederea participarii active la joc;

asigurarea unei atmosphere prielnice de joc;

varietatea elementelor de joc (complicarea jocului, introducerea altor variante);

pregatirea jocului didiactic presupune, în general, urmatoarele:

studierea atenta a continutului acestuia,a astructurii sale;

pregatirea materialului (confectionarea sau procurarea lui);

o alta problema organizatorica este cea a distribuirii materialului necesar desfasurarii jocului. În general, materialul se distribuie la începutul activitatii de joc si aceasta pentru urmatorul motiv: elevii, cunoscând în prealabil materialele didactice necesare jocului respective, vor întelege mai usor explicatia învatatorului referitoare la desfasurarea jocului.

Acest procedeu nu trebuie aplicat în mod mechanic. Exista jocuri didactice matematice în care materialul poate fi împartit elevilor dupa explicarea jocului.

Organizarea judicioasa a jocului didactic are influenta favorabila asupra ritmului de desfasurare a acestuia, asupra realizarii cu success a sopului propus.

Desfasurarea jocului didactic cuprinde, de regula, urmatoarele momente (faze):

. introducerea în joc (discutii pregatitoare);

. anuntarea titlului jocului si a scopului acestuia;

. prezentarea materialului;

. explicarea si demonstrarea regulilor jocului;

. fixarea regulilor;

. executarea jocului de catre elevi;

. complicarea jocului;

. închiderea jocului (evaluarea conduitei de grup sau individuala).

Introducerea în joc , ca etapa, îmbraca forme variate în functie de tema jocului.

Uneori, atunci cand este necesar sa familiarizam elevii cu continutul jocului, activitatea poate sa înceapa printr-o simpla discutie cu effect motivator. Alteori, introducerea în joc se poate face ptintr-o scurta expunere care sa stârneasca interesul si atentia elevilor. În alte jocuri, introducerea se poate face prin prezentarea materialului, mai ales atunci când de logica materialului este legata întreaga actiune a elevilor. Introducerea în jocul matematic nu este un moment totdeauna obligatoriu. Propunatorul poate începe jocul anuntând direct titlul acestuia.

Anuntarea jocului trebuie facuta sintetic, în termini precisi, fara cuvinte de prisos, spre a nu lungi inutil începutul acestei activitati. De exemplu: "Astazi vrem sa vedem care dintre voi stie sa calculeze fara sa greseasca; de aceea vom organizza împreuna jocul..".

Învatatorul poate folosi si formula clasica: "Copii, astazi vor organiza un joc nou. Jocul se numeste.. El consta în..".

Alteori, se poate începe anuntarea printr-o fraza interogativa: "stiti ce o sa ne jucam astazi? Vreti sa va spun?". Învatatorul poate gasi formulele cele mai variate de anuntare a jocului, astfel ca, de la o lectie la alta, ele sa fie cât mai adecvate continutului acestuia.

Un moment hotarâtor pentru succesul jocului didactic matematic este demonstrarea si explicarea acestuia.

Învatatorului îi revin urmatoarele sarcini:

sa faca pe elevi sa înteleaga sarcinile ce le revin;

sa precizeze regulile jocului, asigurând îsusirea lor rapida si corecta de catre elevi;

sa precizeze continutul jocului si principalele lui etape, în functie de regulile jocul;ui;

sa dea explicatii cu privire la modul de folosire a materialului didactic;

sa scoata în evidenta sarcinile conducatorului de joc si cerintele pentru a deveni câstigator.

Fixarea regulilor:

Uneori, în timpul explicatiei sau dupa explicatie, se obisnuieste sa se fixeze, regulile transmise.

Acest lucru se recomanda, de regula, atunci când jocul are o actiune mai complicata, impunându-se astfel, o subliniere speciala a acestor reguli. De multe ori fixarea regulilor nu se justifica, deoarece se împlineste formal, elevii reproducându-le în mod mechanic.

Executarea jocului:

Jocul începe la semnalul conducatorului de joc. La început acesta intervine mai des în joc, reamintind regulile, dând unele informatii organizatorice.

Pe masura ce se înainteaza în joc sau elevii capata experienta jocurilor matematice, propunatorul acorda independenta elevilor, îi lasa sa actioneze liber.

Se desprind, în general doua moduri de a conduce jocul elevilor:

conducerea directa (învatatorul conduce jocul);

conducerea indirecta (învatatorul ia perte la joc fara sa-l conduca);

pe durata unui joc didactic matematic învatatorul poate trece de la conducerea directa la cea indirecta sau le poate alterna.

Totusi, chiar daca învatatorul nu participa direct la joc, sarcinile ce revin sunt deosebite. Astfel, în ambele cazuri, învatatorul trebuie:

sa imprime un anumit ritm jocului (timpul este limitat);

sa mentina atmosfera de joc;

sa urmareasca evolutia jocului, evitând momentele de monotonie;

sa controleze modul în care elevii rezolva sarcina didactica, respectându-se regulile stabilite;

sa creeze conditii necesare pentru ca fiecare elev sa resolve sarcina didactica în mod independent sau în cooperare;

sa urmareasca comportarea elevilor, relatiile dintre ei;

mod independent), schimbarea materialului între elevi (pentru a le da posibilitatea sa resolve probleme cat mai diferite în cadrul aaceluiasi joc), complicarea sarcinilor jocului, introducerea unui element de joc nou, introducerea unui material nou.

Încheierea jocului

În îcheiere învatatorul formuleaza concluzii si aprecieri asupra felului în care s-a desfasurat jocul, asupra modului în care s-au respectat regulile de joc si s-au executat sarcinile primate, asupra comportarii elevilor, facând recomandari si evaluari cu caracter individual si general.

Jocul didactic matematic poate fi organizat cu success la orice tip de lectie si în orice clasa a ciclului primar.

Exemple de jocuri didactice

"Hai sa socotim"

Scopul - consolidarea deprinderilor de calcul oral.

Sarcina didactica - sa rezolve exercitii de adunare si scadere, în limitele 0-100.

Materialul didactic - trei saculete de panza unul galben, unul negru si unul alb;

- cartonase pe care vor fi scrise exercitii de adunare sau scadere în limita 0-100 si apoi introduce în saculetul galben;

- buline albe si negre din carton ce vor fi introduse în saculetele corespunzatoare.

Se stabilesc 2 echipe. Prima pereche, formata din câte un reprezentant al fiecarei echipe, vine în fata clasei si fiecare elev scoate cate un cartonas din saculetul galben. Se rezolva exercitiile, clasa apreciînd daca raspunsurile sunt corecte sau nu. Elevulcare a raspuns bine scoate o bulina din saculetul alb, iar cel care a dat un raspuns gresit scoate o bulina din saculetul negru. Identic se procedeaza si cu celelalte perechi. În final fiecare elev ridica bulina obtinuta, iar conducatorul de joc totalizeaza, pe echipe, numarul si culoarea bulinelor obtinute. Echipa care a obtinut cele mai multe buline albe va fi declarata câstigatoare.

"Cine stie , scrie"

Scopul - dezvoltarea deprinderii de calcul oral si scris.

Sarcina didactica - formularea si rezolvarea unor exercitii de compunere a numerelor naturale în limitele 1-10, citirea si scrierea lor.

Desfasurarea jocului - se înmparte clasa în doua echipe, apoi se formeaza grupe de câte 2 care vor veni la joc pe rând. Reprezentantii echipei A vor lucra în jumatatea stânga a tablei, iar cei din echipa B în jumatatea din dreapta. Prima pereche de elevi, formata din câte un reprezentant din fiecare echipla. Conducatorul jocului indica un numar si cere elevilor de la tabla sa formuleze în scris diferite exercitii de adunare si de scadere al caror rezultat sa fie egal cu numarul dat. Dupa scurgerea a 3-4 minute, se da semnalul de încetare si se face aprecierea rezultatelor. Pentru a mentine treaza atentia elevilor, aprecierea va fi facuta de elevii din banca a echipei adverse. Acesta va primi câte un punct pentru fiecare greseala descoperita. Însumându-se apoi punctele obtinute pentru rezultate bune si pentru depistarea greselilor se declara echipa câstigatoare.

Exemple: conducatorul jocului spune cifra 6.

Exercitii ce se pot scrie:

Acest joc se poate organiza si la celelalte clase, dar trebuie ca numarul indicat sa fie mai mare si sa se foloseasca cele 4 operatii.

Exemplul 1:

Daca se pastreaza un numar mai mic decât 10, dar se cere sa se foloseaca cele 4 operatii.

CERCETAREA PEDAGOGICÃ

Verbul " a cerceta" are mai multe întelesuri: a observa, a examina cu atentie, a întreba, a cauta etc.

Obiectul unei cercetari psihopedagogice îl constituie o problema "un fapt" pe care cercetatorul îl identifica si delimiteaza din ansamblul structural din care face perte, cu intentia de a-i da o explicatie plauzibila si de a obtine date certe privind functionalitatea sa.

Unul dintre faptele pedagogice ce pot constitui obiectul unei cercetari pedagogice poate fi:" Metodele de predare-învatare a operatiilor aritmetice în învatamântul primar".

Succesul în dobândirea cunostintelor privind operatiile aritmetice depinde în mod semnificativde învatator , de felul în care acesta reuseste sa conduca procesul precarii - învatarii si evaluarii, dupa modul cum sunt orientati copii sa poata constientiza descoperii si aplica prin transfer cunostiintele, priceperile si deprinderile.

În procesul de învatare la clasele I-IV trebuie sa se foloseasca metode care creeaza posibilitatea elevului de a transforma cunostiintele pasive în cunostiinte active si de a favoriza descoperirea unor noi cunostiinte cât si aplicarea lor în activitaea practica.

IV.1. Precizarea obiectivelor si formularea ipotezei

În cadrul cercetarii întreprinse am pornit de la urmatoarea ipoteza: jocul didactic prin utilizarea si integrarea adecvata în lectiile de matematica poate duce la cresterea eficientei învatarii notiunilor matematice si prin aceasta cresterea randamentului scolar al elevilor din ciclul primar.

Din ipoteza formulata se desprind 2 variabile a cercetarii:

- variabila independenta-utilizarea jocului didactic în cadrul lectiilor de matematica;

- variabila dependenta- cresterea eficientei însusirii operatiilor aritmetice si implicit a procesului scolar al elevilor.

În vederea demonstrarii acestei ipoteze mi-am propus declansarea unei cercetari psihopedagogice care are ca obiectiv dovedirea eficientei jocului didactic în orele de matematica.

IV.2 Metodica cercetarii

Cercetarea a fost organizata în anul scolar 2007-2008 pe esantioane de elevi de vârsta scolara mica (8-9 ani). Am avut în vedere doua clase a II-a respectiv a II-a de la scoala cu clasele I-IV Vâlcele, clasa experimentala (esantionul de progres) si clasa a II-a de la scoala I-IV Marvila- clasa martor (esantionul de control).

Deoarece mi-am propus sa declansez o actiune educationala rezultatele acesteia fiind înregistrate si prelucrate pentru a demonstra eficienta folosirii jocului didacti , prin metodologia adoptata se va ajunge la descoperirea unor relatii cauzale, am organizat o cercetare experimentala. Experimentarea presupune determinarea cantitativa prin masurare a fenomenelor investigate. Pe aceasta baza ea ofera posibilitatea evidentierii obiective a eficientei noii tehnologii didactice.

Experimentul a reprezentat principala metoda de investigatie. Experimentul pedagogic presupune crearea unor situatii noi , prin introducerea unor modificari în desfasurarea actiunii educationale cu scopul verificarii ipotezei care a declansat aceste inovatii.

Observatia a fost utilizata în perioada premergatoare si în timpul desfasurarii experimentarii. Ea s-a realizat cu scopul de a compara si surprinde comportamentul, reactiile elevilor si mai ales, conditiile psihopedagogice în care jocul didactic asigura învatamântului o deosebita valoare fornativa. Am urmarit , de asemenea, modul în care se adapteaza si este acceptata aceasta metoda de catre elevii cu grade diferite de pregatire.

Probele de evaluare au fost folosite pentru a masura cât mai exact volumul si cunostiintele înainte , în timpul si dupa efectuarea experimentarii.

Testul final a avut un caracter mixt de cunostiinte si aptitudini, verificând atât capacitatea de reproducere a unor cunostiinte cât si nivelul de dezvoltare a capacitatilor de analiza si sinteza de aplicare a cunostiintelor în noi situatii. Punctajul s-a acordat în functie de gradul de dificultate al întrebarii sau problemei si dupa calitatea sau numarul solutiilor gasite sau propuse.

În ceea ce priveste esantionarea am ales doua esantioane: esantion experimental (cls. A II-a de la scoala Vâlcele, 18 elevi) pe care-l voi nota cu Ee si esantionul de control (cls. A II-a scolala Marvila, 16 elevi) pe care-l voi nota cu Ec. Caracteristic pentru esantionul experimental este faptul ca asupra lui se actioneaza cu ajutorul factorului experimental (f.e.) în conformitate cu cele propuse în ipoteza în vederea producerii unor modificari în desfasurarea actiunii educationale. Cel de al II-lea esantion de control este folosit ca martor pentru ca la încheierea cercetarii sa se poata compara rezultatele obtinute pe ambele esantioane si sa se poata conchide pe aceasta baza, ca diferentele se datoreaza factorului experimental.

IV.3. Desfasurarea cercetarii si interpretarea datelor

Primele teste au fost cele de evaluare initiala , în consens cu remarca lui D. Ausubel: Daca as vrea sa reduc toata psihologia la un singur principiu, eu spun: ceea ce conteaza cel mai mult în învatare sunt consecintele pe care le poseda elevul la plecare. Asigurati-va de ceea ce stie si instruiti-l în consecinta.

Metoda de baza utilizata a fost experimentul psihopedagogic de tip experimental- ameliorativ.

Cercetarea a cuprins trei etape:

A. Etapa initiala care a avut un caracter constatativ.

B. Etapa interventiei ameliorative cu valoare formativa în stimularea proceselor psihice si a personalitatii elevilor.

C. Etapa evaluarii ce a avut un caracter comparativ , cu privire la rezultatele obtinute în urma demersului experimental formativ.

Etapa evaluarii a constat în aplicarea unui test de evaluare initiala. Scopul a fost acela de a stabili punctul de plecare în desfasurarea demersului experimental. Testul a fost conceput pentru capitolul "Operatii cu numere naturale în concentrul 0-100" în functie de programa scolara de la clasa a II-a si a obiectivelor operationale vizate în lectie.

Având un caracter constatativ, testul de evaluare initiala reflecta volumul si calitatea cunostiintelor, deprinderilor si priceperilor de calcul aritmetic al elevilor , constituind un punct de pornire în demersul formativ.

Testul a fost aplicat ambelor esantioane.

Unitate de învatare: Operatii cu numere naturale în concentrul 0-100

Continut: Adunarea si scaderea numerelor naturale de la 0 la 100 cu si fara trecere peste ordin.

OBIECTIVE URMARITE

ITEMII TESTULUI

O1 sa se efectueze corect toate adunarile si scaderile date

O2 sa completeze corect semnul de relatie pentru a obtine propozitii adevarate

O3 sa determine corect termenul necunoscut dintr-o expresie data

O4 sa transforme corect un enunt dat într-un exercitiu matematic

O5 sa rezolve corect o problema pe baza unui plan de rezolvare

O6 sa compuna o problema inedita dupa exrcitiul dat

1 Calculati

2. Scrieti unul din semnele "<". ">","="

pentru a obtine relatii adevarate

3. Aflati termenul necunoscut

a+12=30 17+23 -a = 6

4. Cu cât este mai mare suma numerelor 46 si 14 , fata de diferenta lor?

5. Marin are 45 timbre, iar Andrei cu 23 mai putin. Câte timbre au împreuna?

6. Compuneti , apoi rezolvati o problema dupa exrcitiul 40+(40-7)=

Descriptori de performanta

FOARTE BINE	BINE	SUFICIENT
1.Rezolva corect, cu usurinta toate exercitiile date	Rezolva corect majoritatea exercitiilor	Rezolva corect cel putin trei exercitii din cale date
2.Calculeaza corect si foloseste semnul de relatie corespunzator pentru toate exercitiile	utilizeaza corect semnul de relatie la cel putin doua exercitii calculate corect	utilizeaza corespunzator semnul de relatie în cel putin un exercitiu
3. Afla corect termenul necunoscut din toate exercitiile si verifica rezultatele obtinute	Afla corect termenii necunoscuti dar cu sprijin	Afla corect termenul necunoscut din cel putin o expresie data
4. Transforma enuntul în exercitiu si î-l rezolva corect	Transforma enuntul în exercitii pe care le rezolva separat	Transforma enuntul în exercitiu dar nu finalizeaza cerinta
5. Rezolva problema cu plan si rezolvare ; scrie exercitiul problemei	Rezolva problema cu plan si rezolvare	Rezolva partial problema
6. Compune corect problema dupa exercitiu si o rezolva	Compune corect problema dar nu o rezolva	Compune datele dar nu formuleaza întrebarea

Tabel analitic cu rezultatele obtinute în urma aplicarii testului initial la esantionul experimental

Nr. crt	Subiecti	I1	I 2	I3	I4	I5	I6	Calificativ final
	A.M.	F.B.	.B.	B.	B	B.	B.	bine
	B.A.	B.	.S.	I	I	I	I.	Insuficient
	B.I-C.	F.B.	S.	S	S.	S	S	Insuficient
	B.A-s.	F.B.	F.B.	FB.	F.B	F.B.	B	Forte bine
	C.M.	F.B.	F.B.	FB	F.B.	F.B.	B	Forte bine
	D.E.	FB.	B.	B	B	B	B	Bine
	D.A.	B.	B,	S	.B	B	B	Bine
	G.C.I.	S.	S.	I	I	S	I	Insuficient
	J.F.	I.	S	I	S	I	I	Insuficient
	J.M.	B.	S.	B	S	B	B	Bine
	L.S-C.	B.	B,	S	S	B	B	Bine
	P.G-P.	F.B.	B.	B	B	B	F.B.	Bine
	R.D-O.	S.	I.	I	I	I	I	Insuficient
	S.G-B.	B.	S	S	B	S	S	Suficient
	S.A-A.	F.B.	B.	F.B.	F.B.	F.B.	B	Forte bine
	S.I-C.	F.B.	F.B	F.B	F.B.	F.B	F.B.	Forte bine
	T.F.	B.	S	S	S	B	S	Suficient
	V.L.	B.	B	S	S	S	B	Bine
Procent realizat								78% BINE

Tabel analitic cu rezultatele testului initial pe esantionul reprezentativ experimental

Calificative obtinute	Numarul elevilor	Procentaj
Foarte bine
Bine
Suficient
Insufficient

Procentul de realizare a obiectivelor la testului initial pe esantionul reprezentativ experimental

Frecventa de rezultatelor testului initial pe esantionul experimental

Analizând rezultatele înregistrate în tabele s-a constatat ca 78% din elevi stapânesc operatiile de ordin I si terminologia matematica, iar 22% întâmpina greutati la realizarea sarcinilor de la itemii 3, 4 , 6. Un numar de 4 elevi ( cu rezultate foarte slabe) întâmpina dificultati la rezolvarea exercitiilor cu necunoscute ( I3-22% ) , iar alti 3 elevi nu reusesc sa transforme un enunt mathematic în exercitiu(I4-16%) . În ceea ce priveste rezolvarea si compunerea de probleme , elevii folosesc în general operatiile gândirii, doar 14 din ei ajungând la rezultatul corect.

Tabel analitic cu rezultatele obtinute în urma aplicarii testului initial pe esantionul de control.

Nr crt.

Subiecti

Calificativ final

A.L.

F.B.

Bine

A.M.

Suficient

B.A.

Suficient

C.D.

F.B.

Foarte bine

G.D.

Insufficient

H.C.

F.B.

Bine

I.C.

Suficient

M.E.

F.B.

Bine

O.I.

F.B.

Foarte bine

P.I.

F.B.

Bine

R.I.T.

Suficient

S.A.I.

Insuficient

T.D.

F.B.

Bine

Ţ.I-A

Suficient

U.L.

F.B.

Bine

V.L.

F.B.

Foarte bine

Procent realizatA.

Tabel analitic cu rezultatele testului initial pe esantionul de control.

Calificative obtinute	Numarul elevilor	Procentaj
Foarte bine
Bine
Sufficient
Insuficient

Procentajul de realizare a obiectivelor la testului initial pe esantionul de control .

Frecventa rezultatelor la testului initial pe esantionul de control.

Analizând rezultatele graficelor de mai sus s-a constatat ca81% din numarul elevilor stapânesc operatiile de ordinal I si limbajul mathematic, iar19% întâmpina dificultati la realizarea sarcinilor de la itemii 3,6 .Un numar de 3 elevi nu reusesc sa determine o necunoscuta dintr-un exercitiu (I3-81%). La rezolvarea si compunerea de probleme dupa exercitiul dat , doar 12 elevi au finalizat cerinta.

Comparând rezultatele celor doua esantioane la testul initial , situatia se prezinta astfel :

Esantionul experimental si esantionul de control dupa testul initial în procente.

Din alaliza comparativaa rezultatelor obtinute de cele doua esantioane la testul initial s-a constatat ca rezultatele pe clase sunt apropiate (78% esantionul experimental si 81 % esantionul de control). Din punct de vedere a rezultatelor pe calificetive ,s-a constatat ca esantionulexperimental a obtinut un procentaj mai mare la "Forte bine" (4 elevi), decât esantionul de control (3 elevi), la "Bine" esantioanele au obtinut la "Suficient" la esantionul experimental (7elevi) a obtinut un procentaj mai mic(3 elevi), iar la esantionul de control (5 elevi) s-a obtinut un procentaj mai mare .

Primul pas în reorganizarea instruirii l-a constituit aplicarea unor metode active, folosirea unor exercitii-joc si jocuri cu un grad mai mare de complexitate în comunicarea si reactualizarea notiunilor matematice, precum si efectuarea unui numar sporit de exercitii si probleme care sa asigure întelegerea de catre fiecare elev a sarcinilor cerute si posibilitatea rezolvarii cu usurinta a acestora.

B.Etapa interventiei ameliorative a avut un pronuntat caracter formativ , constând în aplicarea jocului didactic în orice tip/varianta de lectie. Am aplicat ambelor clase un test de ameliorare:

- la esantionul experimental (Ee) s-au utilizat atât metode clasice , cât mai ales metoda jocului didactic pentru atingerea obiectivelor propuse;

- la esantionul de control/martor (Ec) lectiile de matematica s-au desfasurat folosindu-se cu precadere de metodele traditionale.

Unitatea de învatare : "Operatii cu numere naturale în concentrul 0-100"

Continut . "Adunarea si scaderea numerelor naturale , cu si fara trecere peste ordin în concentru 0-100"

OBIECTIVE URMĂRITE	ITEMII TESTULUI
O1 sa se rezolve corect toate exercitiile de adunare si scadere date	1. Completeaza locul liber urmarind semnul operatie date :
O2 sa se afle corect termenul necunoscut dintr-un exercitiu dat, astfel încât sa obtina un enunt matematic complet	2. Urmarind semnul + sau - , aflati ce termen lipseste : 68 +a = 99 ; b - 46 = 43
O3 sa utilizeze corect terminologia specifica matematicii în efectuarea exercitiilor	3. La suma numerelor 19 si 28 adaugati diferenta numerelor 51 si15
O4 sa rezolve corect problema, punând-o apoi sub forma de exercitiu	4. la o florarie s-au adus 48 buchete de garoafe rosii si garoafe roz cu 34 mai multe . Câte buchete de garoafe s-au adus în total?
O5 sa compuna si sa rezolve corect o problema folosind exercitiu dat	5. Compune , apoi rezolva o problema dupa exercitiu dat :a + 65 = 98

Descriptori de performanta

FOARTE BINE	BINE	SUFICIENT
I1 rezolva corect toate exercitiile date	rezolva corect majoritatea exercitiile date	Calculeaza corect 2-3 exercitii date
I2 completeaza corect termenul necunoscut din toate exercitiile	completeaza corect toate exercitiile date	Completeaza termenul necunoscut în cel putin o situatie
I3 transforma enuntul într-un exercitiu si îl rezolva correct	transforma enuntul în exercii pe care le rezolva separat	transforma enuntul în exercii, dar nu finalizeaza
I4 alege corect toate numerele si scrie operatia corespunzatoare	alege corect numerele	alege numerele dar cu unele erori
I5 compune corect problema si o rezolva	compune corect problema dar nu finalizeaza rezolvarea	compune corect enuntul problemei, dar nu finalizeaza întrebarea

Tabel analitic cu rezultatele obtinute în urma aplicarii testului de ameliorare pe esantionul experimental

Nr.crt	Subiecti	I1	I 2	I3	I4	I5	Calificativ final
	A.M.	F.B.	F.B.	F.B.	B	F.B.	Forte bine
	B.A.	B.	F.B.	I	S	S	Suficient
	B.I-C.	F.B.	B.	B	F.B.	B	Bine
	B.A-s.	F.B.	F.B.	B.	F.B	F.B.	Forte bine
	C.M.	F.B.	F.B.	B	F.B.	F.B.	Forte bine
	D.E.	B.	B.	S	B	B	Bine
	D.A.	B.	B,	B	F.B	S	Bine
	G.C.I.	B.	B.	B	B	B	Bine
	J.F.	I.	I.	I	I	I	Insuficient
	J.M.	B.	B.	S	S	S	Suficient
	L.S-C.	B.	B,	B	S	S	Bine
	P.G-P.	F.B.	B.	B	B	B	Bine
	R.D-O.	S.	S.	I	I	I	Insuficient
	S.G-B.	B.	B	S	S	S	Suficient
	S.A-A.	F.B.	F.B.	F.B.	F.B.	F.B.	Forte bine
	S.I-C.	B.	B	B	F.B.	B	Bine
	T.F.	B.	S	S	S	B	Suficient
	V.L.	F.B.	B	B	B	B	Calificative obtinute	Numarul elevilor	Procentaj
Foarte bine
Bine
Sufficient
Insuficient

Procentul de realizare la testul de ameliorare pe esantionul experimental .

Frecventa rezultatelor la testul de ameliorare pe esantionul experimental

Din datele înregistrate mai sus , se costata o crestere atât a procentului de realizare a itemilor propusi , cât si a procentului pe clasa de la 78% latestul initial , la 88% la testul de ameliorare. A scazut numarul elevilor cu rezultate nesatisfacatoare (de la 4 la 2) si a crescut numarul elevilor cu rezultate satisfacatoare bune.

Aceasta înseamna nu numai un progress în cunostintele elevilor , ci si în capacitatile lor intelectuale, dat fiind si aportul jocurilor didactice aplicate.

Tabel analitic cu rezultatele obtinute în urma aplicarii testului initial pe esantionul de control.

Nr crt.

Subiecti

Calificativ final

A.L.

f.B.

Bine

A.M.

Bine

B.A.

Insuficient

C.D.

F.B.

Foarte bine

G.D.

Suficient

H.C.

F.B.

Bine

I.C.

Insuficient

M.E.

F.B.

FB.

F.B.

Foarte bine

O.I.

Bine

P.I.

Sufient

R.I.T.

F.B.

Bine

S.A.I.

Insuficient

T.D.

Bine

Ţ.I-A

F.B.

Suficient

U.L.

.B.

Bine

V.L.

F.B.

Foarte bine

Procentaj realizat

Calificativul clasei

Tabel analitic cu rezultatele testului de ameliorare pe esantionul de experimental

Calificative obtinute	Numarul elevilor	Procentaj
Foarte bine
Bine
Sufficient
Insuficient

Procentul de realizare a obiectivelor la testul de ameliorare pe esantionul de control .

Frecventa rezultatelor la testul initial pe esantionul de control

Din datele nregistrate mai sus se constata o stagnare a procentajului pe clasa (81%) a sarcinilor propuse spre rezolvare. A crescut totusi numarul elevilor care au obtinut calificativul "Bine" (de la testul initial, la 7) si a scazut numarul elevilor care au obtinut calificativul "Suficient" (de la 4 la testul initial la 3 ). În acest moment se pot compara rezultatele obtinute de cele doua esantioane la testul de ameliorare. Astfel , promovabilitatea esantionului experimental este de 88% iar al celui de control de 81%.

Pentru a putea interpreta mai bine datele obtinute la testul de control, voi prezenta grafic , în paralel rezultatele pe calificative a celor doua esantioane.

Esantionul experimental Esantionul de control

Esantionul experimental si esantionul de control dupa testul de amelioare

Observând graficele ce reprezinta comparative cele doua esantioane , dupa testul de ameliorare , se constata ca rezultatele obtinute de esantionul experimental sunt situate deasupra celor obtinute de esantionul de control cu 7%. Aceste constatari îmi întaresc convingerea ca masurile aplicate în etapa ameliorativa au fost eficiente, iar continuarea activitatii pe aceasta directie va avea rezultate îmbucuratoare.

Comparând si rezultatele obtinute de cele doua esantioane, la testul initial si la testul de control, situatia se prezinta astfel :

Rezultatele esantionulul experimental la testul initial si testul ameliorative

Rezultatele esantionulul de control la testul initial si testul ameliorativ

Esantionul experimental si-a îmbunatatit rezultatele cu 10 % "Bine"(45% fata de 30%), iar ce este încurajator este scaderea rezultatelor "nesatisfacatoare" cu jumatate din procentajul initial (10% fata de 22%).

Esantionul de control si-a modificat procentajul doar la calificativele "Bine" (45% fata de 30%),si "Suficient" (15% fata de 25%), ponderea numarului calificativelor "Insuficient"ramânând neschimbata.

C. Etapa evaluarii consta în aplicarea unor teste de evaluare finala în scopul compararii rezultatelor obtinute dupa proiectarea si desfasurarea lectiilor cu ajutorul metodei jocului didactic, cu rezultate de la testele initiale.

În lectiile pregatitoare testului final s-a acordat o atentie deosebita eliminarii lacunelor existente în pregatirea elevilor la matematica prin :

- esantionul experimental - continuarea utilizarii jocului didactic; crearea suportului afectiv si motivational necesar participarii active la lectii; aplicarea unui curriculum diferentiat; stimulari si aprecieri pozitive în caz de reusita; jocuri diverse , concursuri pe echipe cu sarcini antrenante;

- esantionul de control(martor)- repetarea cu elevii a notiunilor matematice pe care le retin mai greu, folosindu-se mai des în exercitii si probleme la clasa si acasa în conditii scolare obisnuite.

Testul de evaluare finala si-a propus sa îndeplineasca obiective asemanatoare testului initial, însa cuprinzând sarcini de mai mare dificultate.

Unitatea de învatare: Operatii cu numere naturale în cocentrul 0-100.

Continut :"Efectuarea operatiilor de adunare si de scadere cu trecere peste ordin si aflarea termenului necunoscut".

OBIECTIVE URMĂRITE	ITEMII TESTULUI
O1 sa stabileasca valuate de adevar într-un exercitiu în care apar operatii de adunare si de scadere	I1Adevarat sau fals?
O2 sa completeze corect termenul necunoscut într-un exercitiu dat respectând regulile de calcul	I2 Radu a vrut sa afle valuate literelor din urmatoarele exercitii.Ajutal sa calculeze corect! a +12=64 , m-15=48, 95-n=27
O3 sa utilizeze corect terminologia matematica în efectuarea exercitiilor	I3 Cu cât este mai mica suma numerelor 34 si 28 , decât diferenta numerelor 96 si 27?
O4 sa exprime corect rezolvarea problemei date, prin plan si rezolvare	I4 O carte are 96 de pagini :Ionela citit în prima zi 29 de pagini, iar a doua zi 35 de pagini. Câte pagini mai are de citit Ionel?
O5 sa compuna o problema asemanatoare modificând datele	I5 Schimba datele problemei de mai sus si compune o problema asemanatoare

Descriptori de performanta

FOARTE BINE	BINE	SUFICIENT
I1 rezolva corect toate exercitiile date	Rezolva corect un exercitiu si partial pe al doilea	Rezolva corect un exercitiu
I2 completeaza corect toti termenii necunoscuti	Completeaza termenii necunoscuti dar cu sprijin	Completeaza corect 1-2 termeni necunoscuti
I3 utilizeaza corect terminologia matematica în rezolvarea tuturor exercitiilor	Utilizeaza corect terminologia matematica în rezolvarea a doua exercitii	Utilizeaza corect terminologia matematica dar nu finalizeaza rezolvarea
I4 rezolva corect problema data, transformând planul într-un exercitiu	Rezolva corect problema data fara sa transforme planul într-un exercitiu	Rezolva partial problema data
I5 modifica corect datele problemei, respectând cerinta	Modifica datele si finalizeaza calculul	Modifica ,dar nu finalizeaza calculul

Tabel analitic cu rezultatele obtinute în urma aplicarii testului final pe esantionul experimental

Nr.crt	Subiecti	I1	I 2	I3	I4	I5	Calificativ final
	A.M.	F.B.	F.B.	F.B.	B	F.B.	Forte bine
	B.A.	B.	B.	S	B	B	Bine
	B.I-C.	B.	F.B.	FB	B.	F.B	Forte bine
	B.A-s.	.B.	F.B.	F.B.	B	F.B.	Forte bine
	C.M.	F.B.	F.B.	B	F.B.	F.B.	Bine
	D.E.	FB.	B.	B	FB	B	Bine
	D.A.	B.	S,	S	S	S	Suficient
	G.C.I.	FB.	B.	B	FB	B	Bine
	J.F.	S	S	I	S	S	Suficient
	J.M.	FB.	FB.	B	B	B	Bine
	L.S-C.	B.	F.B,	B	F.B.	F.B.	Foarte Bine
	P.G-P.	B.	FB.	FB	FB	FB	Foarte Bine
	R.D-O.	B.	B.	S	S	I	Suficient
	S.G-B.	FB.	FB	B	B	B	Bine
	S.A-A.	.B.	F.B.	F.B.	F.B.	F.B.	Forte bine
	S.I-C.	F.B.	F.B	F.B	.B.	F.B	Foarte Bine
	T.F.	B.	F.B.	B	B	B	Bine
	V.L.	B.	B	B	B	B	Calificative obtinute	Numarul elevilor	Procentaj
Foarte bine
Bine
Sufficient
Insuficient

Procentul de realizare a obiectivelor la testul final pe esantionul experimental

Frecventa rezultatelor la testul final pe esantionul experimental

Analizând rezultatele înregistrate de mai sus e usor de remarcat ca numarul elevilor care au obtinut rezultate bune(50%) si foarte bune(33,33%) a crescut semnificativ,(9,respective 6 elevi). De asemenea absenta rezultatelor nesatisfacatoare dovedesc ca elevii si-au însusit bine cunostintele de la acest capitol , calculeaza cu usurinta suma, diferenta, numerele naturale. Afla numarul necunoscut dintr-o expresie data, cunosc terminologia specifica matematicii si rezolva cu usurinta problemele cu mai multe operatii. Cei 9 elevi care au obtinut calificativul "Bine" (50%) dovedesc acelasi lucru, ei negresind la tehnica de lucru , ci la unele calcule effectuate în graba. Unele lacune le prezintacei 3 elevi care au obtinut calificativul "Suficient"(16,66%). Ei dovedesc nesiguranta la rezolvarea exercitiilor si nu stapânesc bine limbajul mathematic.

Tabel analitic cu rezultatele obtinute în urma aplicarii testului final pe esantionul de control.

Nr crt.	Subiecti	I1	I2	I3	I4	I5	Calificativ final
	A.L.	B.	FB.	B.	f.B.	B.	Bine
	A.M.	FB.	F.B.	FB.	FB.	FB.	Foarte bine
	B.A.	S.	B.	B.	S,	S.	Suficient
	C.D.	F.B.	FB.	B.	F.B.	F.B.	Foarte bine
	G.D.	S.	S.	I.	I.	I.	Insuficient
	H.C.	F.B.	B.	S.	FB.	B.	Bine
	I.C.	F.B.	B.	S.	S.	I.	Suficient
	M.E.	.B.	FB.	FB.	FB.	F.B.	Foarte bine
	O.I.	B.	B.	B.	B.	B.	Bine
	P.I.	I.	S.	I.	I.	I.	Insuficient
	R.I.T.	S.	B.	S.	S.	S.	Suficient
	S.A.I.	S.	S.	S.	S.	S.	Suficient
	T.D.	S.	B.	B.	B.	B.	Bine
	Ţ.I-A	F.B.	B.	B.	F.B..	B.	Bine
	U.L.	F.B.	FB.	FB.	B.	B.	Foarte bine
	V.L.	F.B.	F.B.	S.	.B.	S.	Bine
Procentaj realizat Calificativul clasei							Calificative obtinute	Numarul elevilor	Procentaj
Foarte bine
Bine
Suficient
Insuficient

Procentul de realizare a obiectivelor la testul final pe esantionul de control

Frecventa rezultatelor la testul final pe esantionul de control

Din rezultatele transpuse în graficele de mai sus s-a constatat ca 87% din numarul total al elevilor au obtinut calificativede trecere a testului (25%-F.B. 4 elevi, 44% B. 7 elevi, 18% S 13 elevi, iar restul de 12% 12 elevi întâmpina înca dificultati de calcul si de tehnica în rezolvarea exercitiilor si problemelor. Nu stapânesc limbajul mathematic si de aceea transpunerea în exercitiu a unui enunt este o greutate pentru ei. Astfel , promovabilitatea primului esantion este de 100% iar celui de-al doile de 87%.

Pentru a putea interpreta mai bine datele obtinute la testul final, voi reprezenta grafic, în parallel, rezultatele obtinute de cele doua esantioane.

Esantionul experimental

Esantionul de control

Esantionul experimental si esantionul de control dupa testul final

Observând graficele ce reprezinta comparative cele doua esantioane, dupa testul final, se constata ca rezultatele obtinute de primul esantion sunt deasupra celor obtinute de al doilea cu 12,5%. Calculul mathematic si transpunerea limbajului din exercitii si probleme au fost bine însusite acolo unde tehnica de învatare a fost sprijinita de folosirea jocului didactic.

Comparând si rezultatele obtinute de cele doua esantioane , la testul inisial si la testul final, situatia se prezinta astfel :

Rezultatele obtinute la testul initial si testul final de esantionul experimental

Esantionul experimental si-a îmbunatatit cota de rezultate "Bune" (de la 39% la 50%)si "Forte bune"(de la 22% la 32%), iar ceea ce este de remarcat este absenta calificativelor "Insuficient" la testarea finala.

Esantionul de control si-a îmbunatatit cu putin rezultatele , fara salturi majore la un anume calificativ. Rezultate "Foarte bune"(de la 18% la 25%), "Bune"(de la 39% la 44%) si "Insuficiente" (de la 18% la 13 %).

Comparând rezultatele obtinute la cele 3 teste aplicate , s-a constatat ca progresul este semnificativ la esantionul experimental.

CALIFICATIVE OBŢINUTE	TESTUL INIŢIAL	TESTUL DE AMELIORARE	TESTUL FINAL
FOARTE BINE	4 elevi	4 elevi	6 elevi
BINE	7 elevi	8 elevi	9 elevi
SUFICIENT	3 elevi	4 elevi	3 elevi
INSUFICIENT	4 elevi	2 elevi	0 elevi

Prezentarea comparativa a rezultatelor obtinute la cele trei teste evidentiaza evolutia elevilor. Se observa ca dincei 4 elevi care au obtinut calificativul "Insuficient" la testul initial, niciunul nu a ramas la acest calificativ la testul final,: 3 elevi au obtinut "Suficient" , iar unul "Bine". Cresterea numarului de elevi care au obtinut calificativul "Foarte bine" este iarasi semnificativ. Daca la primul test doar 4 elevi primisera acest calificativ, la ultimul test numarul acestora s-a ridicat la 6(o crestere de 10 %) . Procentajul calificativelor "Foarte bine" de la 22% la 33% indica faptul ca metoda jocului didactic aplicata în lectiile de învatare, de consolidare si de evaluare au avut o mare eficienta.

Prezentarea comparativa a rezultatelor obtinute de esantionul experimental la testul initial si testul final

Concluzii

Evaluarea a asigurat o modalitate distincta de analiza cantitativa si calitativa a rezultatelor învatarii pe parcursul întregii etape experrimentale .

Jocul a constituit pentru elevi o modalitate stimulativa, de antrenare la lucru, de motivare a învatarii.

În urma experimentului efectuat putea spune ca utilizarea jocului didactic satisface cerintele unui învatamânt formative, deoarece antreneaza majoritatea elevilor , sporeste gradul de motivatie a învataturii prin satisfactiile pe care elevii le obtin prin rezultatele pozitive ale muncii lor.

Progresul elevilor este evidentiat de cresterea gradului de realizare a obiectivelor instruirii, cresterii materializata în marimea valorii notelor pentru nivelul de cunostinte si deprinderii atins. În acest sens ilustrarea grafica este convingatoare.

La orele de matematica am realizat lectii la care elevii sa participle cu placere si sa-si însuseasca cunostintele în functie de posibilitatile lor intelectuale.

Prin multitudinea de jocuri didactice pe care le-am folosit am reusit sa realizez sarcina învatarii:

- însusirea de cunostinte matematice atât de necesare etapelor urmatoare ale învatarii matematicii.

Prin testele aplicate am cautat sa ilustrez importanta jocului didactic la orele de matematica, faptul ca elevii rezolva cu mai mult interes si placere jocurile care nu sunt altceva decât exercitii si probleme prezentate sub alta forma.

Lectiile organizate cu introducerea uni joc didactic matematic au asigurat participarea activa a elevilor la dobândirea cunostintelor, la formarea unui stil de munca intellectual, lectia devenind o modalitate de organizare a activitatii de învatare.

Cresterea nivelului de pregatire a elevilor prin folosirea jocurilor didactice demonstreaza utilitatea lor , atât la matematica cât si la alte discipline.

Combinând metodele clasice cu cele moderne , adoptând cele mai eficiente strategii didactice, se poate insufla elevilor dragostea pentru matematica , sa-si formeze deprinderi de rezolvare a problemelor de aritmetica, sa-si dezvolte gândirea , logica , imaginatia.

Din experienta didactica din experimental realizat si din bibliografia studiata , pot afirma ca predarea-îmvatarea operatiilor aritmetice are urmatoarele valente:

-dezvolta gândirea, antrenândoperatiile logice de analiza si sinteza, de comparatie, de abstractizare si generalizare;

-dezvolta vointa, perseverenta, spiritual de raspundere, încrederea în fortele proprii;

- stimuleaza initiativa, încrederea în sine, curajul;

- stimuleaza si formeaza priceperi si deprinderi practice.

În urma documentarii pe baza bibliografiei consultate , a experientei didactice si aprobelor de evaluare aplicate, s-a ajuns la urmatoarele concluzii:

- predarea-învatarea operatiilor aritmetice trebuie privita ca un fenomen complex, dar unitar, care angajeaza plenar întreaga personalitate umana;

- compunerea si rezolvarea de problem dezvolta creativitatea ca dimensiune psihologica ce este universal existenta, distribuindu-se în rândul tuturor copiilor dezvoltati normal.

În cadrul matematicii , predarea-învatarea operatiilor aritmetice cu numere naturale are bogate valente formative, fiind o modalitate princioala de a dezvolta gândirea independenta a copiilor.

În scopul stimularii potentialului creative al elevilor, învatatorul trebuie sa fie cel putin neutru fata de evolutia acestuia, în sensul de a nu-iînabusi manifestarile si dezvoltarea , sa intervina constient s iactiv pentru îndepartarea blocajelor obiective si subiective ale creativitatii elevilor, sa preia si sa dezvolte în mod organizat potentialul creativ al fiecarui copil.

E absolute necesar ca învatatorul sa cunoasca pe cât posibil situatia potentialului psihologic al fiecarui elev în parte, se impune astfel masurarea prin diferite probe si modalitati a potentialului creativ al copiilor, aceste probe sa aiba doua faze: initiala si finala-în intervalul de timp dintre ele lucrându-se intens cu elevii; rezultatele finale vor reda progresul obtinut de elevi în ceea ce priveste însusirea cunostintelor, dar si în ceea ce priveste dezvoltarea capacitatilor creatoare (astfel de probe se pot aplica la început si la sfârsit de capitol, semestru sau an scolar).

Rezultatele obtinute ofera informatii detaliate care pot fi luate în calcul la elaborarea masurilor ameliorative pentru elevi astfel: elevii cu capacitati reduse de întelegere si asimilare vor primi spre rezolvare sarcini de nivel reproductive si de cunoastere pentru a-i ajuta sa realizeze obiectivele programei ; iar celor cu potential creative, li se vor crea conditii propice , în care sa li se poata dezvolta nestânjenit capacitatile creative.

Prin aceste probleme de evaluare se realizeaza o eficienta conexiune inversa ; învatatorul cunoaste despre fiecare elev ce stie si ce nu stie din capitolul respectiv, iar elevii devin constienti de ceea ce au realizat.

Modul de prezentare al unor itemi în probele aplicate (alegerea raspunsului corect din mai multe posibilitati, stabilirea adevarului sau falsitatii unei propozitii matematice, completarea problemei cu date si întrebari noi, compunerea de probleme) au trezit interesulcopiilor si dorinta exprimata de a mai primi astfel de sarcini.

În însusirea cunostintelor de catre elevi un rol important îl are munca independenta, în ora de matematica elevii trebuie sa lucreze , sa faca efort nu numai aplicativ, cât mai ales mintal creator. În cadrul activitatii independente din clasa , trebuie sa realizam si învatarea în ritm propriu, deoarece într-o clasa de elevi exista mai multe nivele de gândire si ritmuri de lucru variate , specifice fiecarui copil.

Este necesar ca elevii sa fie obisnuiti ca singuri sa caute de lucru, sa creeze probleme si exercitii pe care sa le resolve si în felul acesta ora de matematica sa fie o ora densa , în care elevii sa lucreze mai mult, învatatorul lucrând cu clasa cât si cu fiecare elev în parte, astfel elevii înteleg ca matematica este o stiinta a realitatii înconjuratoare , indispensabila diverselor activitati umane practice, nu e doar o activitate abstracta pura.

Principiul participarii constiente si active a elevilor în procesul de învatamânt este unul din cele mai importante principii ale didacticii, exprimând esenta procesului învatarii în acceptie moderna si având cea mai mare participare la realizarea eficientei formative a învatamântului. Însusire constienta a cunostintelor asigura temeinicia lor, iar însusirea activa prin efort propriu , duce la dezvoltarea inteletuala în primul rând a gândirii, precum si la dezvoltarea spiritului de independenta, de investigatie, de creativitate. A-i învata pe elevi cum sa învete a devenit o problema majora a scolii. Iata de ce un loc important în formarea si dezvoltarea la elevi a capacitatilor de creatie îl ocupa învatarea prin descoperire si redescoperire.

Toate aceste achizitii ale elevilor sunt permise minime pentru orice act de creatie , baza a oricaror creatii viitoare si a comportamentului creativ.

Lucrarea de fata face simtita armonia interioara a matematicii, capabila sa trezeasca constiinta ca exista probleme matematice atragatoare , pentru întelegerea carora nu este nevoie de un talent special si nici o pregatire care sa depaseasca nivelul claselor elementare.

Consider ca scopul propus a fost confirmat si ca predarea-învatarea operatiilor aritmetice se datoreaza în mare parte atât capacitatilor intelectuale ale elevilor cât si însusirii corecte a metodelor diverse de predare a acestor cunostinte.

BIBLIOGRAFIE

1.Aron, Ioan- "Metodicxa predarii matematicii la clasele I-IV, manual pentru liceele pedagogice" , Editura Didactica si Pedagogica Bucuresti 1972.

2.Ausubel, D.P. ; Robinson , F.G. - "Învatarea scolara , o introducere în psihologia pedagogica", Editura Didactica si Pedagogica Bucuresti 1981.

3. Barbieru Nadia, Pituru Ecaterina, Carbunaru Viorica- "Matematica. Ghidul învatatorului, clasa I", Editura Teora, Bucuresti 2000.

4. Cerghit Ioan- "Metode de învatamânt", Editura Didactica si Pedagogica Bucuresti 1980, editia a II-a , revazuta si adaugita.

5.Cerghit Ioan " Perfectionarea lectiei în scoala moderna" Editura Didactica si Pedagogica Bucuresti 1983.

6. Cojocariu Venera- Mihaela- " Teoria si metodologia instruirii", Editura Didactica si Pedagogica Bucuresti 2004.

7. Cosmovici Andrei -"Psihologia generala" , Editura Polirom Iasi 1996

8. Cretu Carmen , "Curriculum diferentiat si personalizat" Metode didactice, Editura Polirom Iasi

9.Cristea Sorin " Dictionar de pedagogie" Editura Litera Educational , Chisinau 2002

10.Cristea Sorin "Pedagogie pentru pregatire examenelor de definitivare, grade didactice, reciclare" , Eduâitura Hardiscom 1997

11. Cucos Constantin (coord)-"Psihopedagogie pentru examenele de definitivare si grade didactice " Editura Polirom ,Iasi, 1998

12. Debesse M. " Etapele educatiei", traducerea de MAgdalena Chelsoi, Editura Didactica si Pedagogica Bucuresti 1981

13. Dottrens R, Miliaret G., Rast E., Rai M.,-" A educa si a instrui" , Editura Didactica 1970

14. Dragan I., Nicola I., "Cercetare psihopedagogica" Editura Tipomur , Târgu Mures 1993

15. Dumitriu Constanta , "Introducere în cercetarea psihopedagogica". Editura Didactica si Pedagogica Bucuresti 2004

16. Golu Pantelimon , Zlate Mielu, Verza Emil - " Psihologia Copilului " Manual pentru clasa XI-a , scoli normale , Editura Didactica si Pedagogica Bucuresti ,1993

17.Gugiuman A. si colaboratorii - "Introducere în cercetarea pedagogica", Editura Tehnica , Chisinau 1993

18. Herescu Gh., Dumitru A., Aron I., - "Matematica pentru învatatori", Editura Didactica si Pedagogica Bucuresti 1996

19. Joita Elena- "Didactica aplicata. Învatamântul primar.partea I", Editura Gheorghe Alexandrescu , Craiova 1994

20.Lupu Costica, Savulescu Dumitru- "Metodica predarii matematicii. Manual pentru clasa a IX-a licee pedagogice " , Editura Paralela 45 , Pitesti 1998

21. Lupu Costica , "Metodica predarii matematicii. Manual pentru clasa a XII-a licee pedagogice "Editura Paralela 45 , Pitesti 1998

22. Lupu Costica- " Didactica matematici" Editura Coba , Bucuresti 2006

23. Lupu Costica, Savulescu Dumitru, Lupu Ioan , "Aritmetica: teorie , probleme, metode de rezolvare" Editura Egal, Bacau 2002

24.Neacsu Ion -" Metode si tehnice de învatare eficienta" Editura militara Bucuresti 1990

25.Necsu Ion si colaboratorii- "Metodica predarii matematicii la clasele I-IV. Manual pentru liceele pedagogice clasele XI-XII" Editura Didactica si Pedagogica Bucuresti ,1998

26. Neveanu P.P., (coord), Zlate Mielu, Cretu Tinca- "Psihologie. Manual pentru clasa a XI-a , scoli normale si licee", Editura Didactica si Pedagogica Bucuresti ,1997

27.Neveanu P.P. -"Dictionar de psihologie", Editura Albatros Bucuresti 1978

28. Nicola Iona -"Tratat de Pedagogie scolara" Editura Didactica si Pedagogica Bucuresti ,1996

29. Radu I.T.- "Teorie si practica în evaluarea eficientei învatamântului",

Editura Didactica si Pedagogica Bucuresti ,1981

30.Radu Nicolaie, Singer Mihaela- "Matematica , clasaI.Ghid pentru anvatatori si parinti", Editura Sigma Bucuresti 2004

31.Singer Mihaela- "Matematica , manual pentru clasa I", Editura Sigma Bucuresti 2004

32. Singer Mihaela -"Învatarea matematici în scoala primara-perspectiva noilor programe", Revista de pedagogie , nr.4 1998

33.schiopu Ursula- "Psihologia Generala a Copilului" ,Editura Didactica si Pedagogica Bucuresti ,2001

34.Telinou P., "Culegere de exercitii si probleme de aritmetica", Editura Porto-Franco, Galati 1991

35. XXX Serviciul National de evaluare si examinare, Consiliul National pentru Curriculum-Descriptori de performanta pentru învatamântul primar", Editura pro-Gnosis, Bucuresti 2001.

PROIECT DIDACTIC

DATA: 14.XII.2007

CLASA a II-a

sCOALA CU CLASELE I-IV VÎLCELE

ÎNVĂŢĂTOR:

OBIECTUL:MATEMATICĂ

ARIA CURRICULARĂ:MATEMATICĂ sI sTIINŢE

CURRICULUM: NUCLEU

UNITATEA DE ÎNVĂŢARE:Adunarea si scaderea numerelor naturale de la 0 la 100 cu si fara trecere peste ordin.

SUBIECTUL:Adunarea cu trecere peste ordin a numerelor naturale de la 0 la 100

SCOPUL LECŢIEI:Formarea priceperilor si deprinderilor de a calcula corect folosind operatiile de adunare si scadere în cocentrul 0-100

TIPUL LECŢIEI:Consolidare

OBIECTIVE OPERAŢIONALE:

O1-sa efectueze calcule dupamodel

O2-sa rezolve exercitii de adunare, cu trecere peste ordin

O3-sa verbalizeze procedeul de calcul

O4-sa utilizeze terminologia specifica (termen, suma, diferenta, "cu atât mai mult", "cu atât mai putin")

O5-sa lucreze în echipa

O6-sa îsi dezvolte spiritul competitiv

STRATEGIA DIDACTICĂ:-algoritmica

METODE sI PROCEDEE:-algoritmizarea

-conversatia

-exercitiul

-explicatia

-munca independenta

-problematizarea

MIJLOACE DIDACTICE: -manualul

-caietul special

-culegeri

-fise de lucru

FORME DE ACTIVITATE: -frontala

-individuala

-în echipa

-jocul didactic

BIBLIOGRAFIE:-Programa scolara pentru învatamântul primar

-Neagu ,M.,Petrovici C.2001,Elemente de didactica matematicii în gradinita si învatamântulprimar, Editura AS"S Iasi

-Simionica E., Caraiman F.,1998, Matematica... prin joc, Editura Polirom Iasi

SECVENŢELE LECŢIEI

OB.

OP.

CONŢINUTUL INSTRUCTIV-EDUCATIV

METODE PROCEDEE

EVALUARE

I.Momentul organizatoric

II.Verificare temei

III.Anuntarea titluluii

IV.Reactualizarea elementelor de teorie învatate

V.Dezvoltare competentelor de calcul

VI.Consolidarea deprecierilor de calcul scris

VII.Aprecieri asupra desfasurarii activitatii didactice

Organizarea clasei pentru participarea activa la lectie

Mai multi elevi citesc enuntul si rezultatele exercitiilor, un elev citeste problema si rezolvarea

Astazi vom efectua exercitii de adunare a numerelor de la 0 la 100 cu trecere peste ordin. -explic obiectivele pe întelesul copiilor. Scriu data, titlul pe tabla, iar elevii pe caiete.

cum se numeste rezultatul adunarii? Dar numerele care se aduna?

Cum se numeste rezultatul scaderii? Dar numerele care se scad?

Exercitii de calcul oral:

(se începe cu exercitii usoare, schimbându-se progresiv gradul de dificultate)

- numara :

din2 în 2 , de la 18 la 36;

din 5 în 5 de la 30 la 55

- mareste pe :30 cu 20; 22 cu 11;...

- micsoreaza pe 10 cu 8, 27 cu 10, 44 cu 22, ...

-Într-un bradut sunt 10 globuri rosii, 5 albastre, 3 verzi si 2 galbene. Câte globuri sunt în bradut?

Exercitii de calcul scris

1.Adunati, respectând modelul:

2.Care este numarul cu 19 mai mare decât 65?

3.Aflati suma a+b+c=52 stiind ca a=11, b=15 iar c=a+b

c=a+b=11+15=26

a+b+c=11+15+26=26+26=52

Joc didactic

Concurs pe echipe

Elevii vor fi grupati câte patru în echipa(pe culori, rosu, galben, verde, albastru),apoi vor primi explicatiile necesare privind regulamentul jocului.

Ei vor trebui sa calculeze adunari si scaderiîn lant, acestea fiind scrise pe tabla pentru fiecare echipa.

Scopul jocului: de consolidare a deprinderilor de calcul;

-de formare a abilitatilor de lucru în echipa;

-de dezvoltare a spiritului competitiv.

Câstiga echipa care termina prima, efectuând corect sirul de calcule.

Echipa câstigatoare primeste aplauzele întregii clase se rechizite.

Exercitii de rezerva

1. Uneste operatia cu rezultatul corect:

2.Iulia are 23 de bomboane de ciocolata si 16 cu alune. Daca mai primeste 27 cu ciocolata si 14 cu alune , câte bomboane va avea de fiecare fel? Dar în total?

Se fac aprecieri generale privind activitatea elevilor la ora. Se evidentiaza cei cu o implicare mai mare.

Tema pentru acasa: Fisa de lucru.

conversatia

exercitiul

exercitiul

de calcul

exercitiul

activitatea în echipa

conversatia

explicatia

activitatea în echipa

evaluare frontala

aprecieri verbale

procedee

evaluare individuala

evaluare frontala

problematizarea

evaluare frontala si individuala

aprecieri verbale

premierea echipei câstigatoare

se acorda calificative

explicatia

demonstratia

FIsA DE LUCRU

1. Efecueaza operatiile de mai jos.

2. La suma numerelor 25 si 18 aduna pe 9.

3.Afla numerele cu 17 mai mari decât : 35, 46, 57, 68 si 79.

4. Eugen are 28 de cuburi , iar Florin cu 5 mai mult. Câte cuburi are Florin?

5.Compune o problema despre cartile din biblioteca, pe care sa o rezolvi prin adunare.

Document Info

Accesari: 103424
Apreciat:

Comenteaza documentul:

Nu esti inregistrat
Trebuie sa fii utilizator inregistrat pentru a putea comenta

Creaza cont nou

A fost util?

Daca documentul a fost util si crezi ca merita
sa adaugi un link catre el la tine in site

Copiaza codul:
in pagina web a site-ului tau.

eCoduri.com - coduri postale, contabile, CAEN sau bancare

Politica de confidentialitate | Termenii si conditii de utilizare