Curenti de magnetizare

1.Curenti de magnetizare

Consideram o bara cilindrica în care dipolii magnetici atomici , distribuiti uniform sunt orientati dupa o directie paralela cu axa cilindrului. Spunem ca bara este uniform magnetizata, vectorul de magnetizare fiind orientat paralel cu bara.

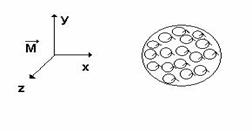
În interiorul barei curentii atomici vecini se anuleaza reciproc, având sensuri opuse. La suprafata ei însa acesti curenti nu se mai anihileaza, existând un curent net, ceea ce echivaleaza bara uniform magnetizata cu un solenoid lung parcurs de curent. Daca ne imaginam o folie transversala de material, 19119x2318t de grosime , fiecare bucla poseda un moment magnetic.

,

de unde extragem curentul : . Spunem ca acesti curenti se anihileaza în material, dar nu la suprafata, unde vom avea o densitate superficiala de curent :

În cazul în care vectorul de magnetizare nu este uniform,, vom arata ca apare în substanta un curent de magnetizare: .

Pentru aceasta sa împartim suprafata în mici blocuri presupuse având o magnetizare uniforma în interior, valoarea magnetizarii suferind mici salturi când treceam de la un bloc la altul. Apoi vom considera fiecare bloc echivalent cu o panglica de curent parcursa de intensitatea . Blocul vecin (pe directia ) e parcurs de un curent mai mare , astfel încât, la interfata celor doua blocuri va exista un curent net dat de diferenta:

,

Densitatea de curent corespunzatoare (pe directia ) se obtine raportând curentul la aria transversala pe care o strabate perpendicular. În cazul descris aceasta este nula. În realitate însa, variatia lui nu se face în salturi ( când ne deplasam pa directia ) ci continuu si atunci interfata dintre blocuri nu mai este un plan ci se extinde la un domeniu de arie :

O contributie la densitatea de curent mai exista si datorita variatiei componentei a magnetizatiei când ne deplasam pe directia : , blocurile fiind acum asezate unul peste celalalt. Combinând cele doua contributii obtinem:

Analog se obtin componentele , demonstrând relatia:

2. Ecuatiile lui Maxwell în substanta

Sa consideram legea lui Ampere completata de Maxwell :

Daca în acel mediu avem si un curent de conductie , si un curent de polarizare si un curent de magnetizare

, putem exprima densitatea de curent ca o numa :

Înlocuind în ecuatie, obtinem :

,

.

Amintindu-va ca - inductia câmpului electric si definind - intensitatea câmpului magnetic, legea lui Ampere completata de Maxwell se rescrie sub forma :

.

3. Câmpuri statice.

Vom considera câmpurile care nu depind de timp. Ecuatiile lui Maxwell:

,

,

,

,

devin :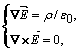 si 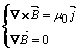, adica se produce o deplasare a vectorilor si daca densitatea volumica de sarcina si curentii nu depind de timp.

3.1 Electrostatica.

Când vectorul depinde numai de pozitie, ecuatiile lui Maxwell se scriu: si . Cea de-a doua ecuatie ne ofera posibilitatea introducerii functiei potential scalar () prin relatia. (Într-adevar, , pentru orice functie scalara .Înlocuind în prima ecuatie Maxwell, obtinem:

, ecuatia lui Poisson, sadisfacuta de catre potentialul scalar din care deriva câmpul.

În absenta sarcinilor electrice , ecuatia lui Poisson se transforma în ecuatia lui Laplace : , a carui solutie nu poate avea extreme (matematic, aceasta înseamna ca derivatele partiale de ordinul doi: sa aiba acelasi semn).

Cautam acum solutia ecuatiei Poisson.Pentru început vom considera o sarcina punctiforma si vom determina intensitatea câmpului produs la distanta de ea cu ajutorul teoremei lui Gauss. Vom considera o suprafata gaussiana de forma sferica, (din considerente de simetrie) , de raza , având în centru sursa, si vom calcula fluxul câmpului electric :

(legea lui Coulomb)

Potentialul scalar al câmpului produs de sarcina în punctul situat la distanta este dat de relatia :

.

În cazul în care avem un sistem de sarcini punctuale, principiul superpozitiei afirma ca potentialulcâmpului rezultat într-un punct în mod independent de catre fiecare sursa în parte.

Daca sarcinile nu sunt punctiforme ci au o distributie continua descrisa de densitatea volumica de sarcina , potentialul rzultat într-un punct din spatiu va fi :, unde este distanta de la elementul de volum la punctul în care calculam potentialul. Astfel pe o cale ocolita am aflat solutia ecuatiei Poisson : .

3.2.Magnetostatica

În cazul curentilor stationari ( nu depinde de timp ) ecuatiile lui Maxwell pentru câmpul magnetic sunt :

si .

Cea de-a doua ecuatie ne permte introducerea potentialului vector prin relatia : , deoarece , oricare ar fi functia vectoriala . Înlocuind în prima ecuatie obtinem :

,

si apicând relatia cunoscuta : , avem :

sau grad .

Impunem potensialului vector al câmpului conditia :

el nefiind univoc determinat. Acum va satisface ecuatia lui Poisson :

.

Deoarece ecuatile similare au solutii similare, vom gasi :

,

unde R este distanta de la elementul de volum la punctul în care calculam . Putem acum sa determinam inductia câmpului magnetic prin relatia:

,

Pentru a calcula aceasta expresie vom folosi identitatea :

, unde este o functie scalara si este o functie vectoriala. În cazul nostru, vom considera si : .

Expresia se anuleaza deoarece operatorul rotor contine derivatele partiale în raport cu coordonatele ale punctului de observatie în timp ce functia vectoriala depinde de coordonatele locului unde sunt curentii, surse de câmp.

Acum,

si expresia devine , Conducând la rezumatul :

,

Cunoscut sub numele de legea lui Biot-Savart. El permite aflarea câmpului magnetic produs de o distributie cunoscuta de curenti.

3.3. Curentul electric stationar

3.3.1. Tensiunea electromotoare

Miscarea ordonata a sarcinilor libere într-un mediu conductor se numeste curent de conductie. În majoritetea materialelor densitatea de curent este proportionala cu forta care actioneaza asupra unitatiide sarcina :

,

unde se numeste conductivitatea electrica materialului, iar este rezistivitatea electrica a acestuia (în cazul dielectricilor , pentru semiconductori si pentru metale ) .

Daca forta care transporta sarcinile este de natura electromagnetica (forta Lorentz), ea are expresia

,

iar pentru viteze mici termenul se neglijeaza si obtinem forma locala a legii lui Ohm.

În teoria electrica în care electronii de conductie au o miscare haotica , asemenea moleculelor unui gaz, expresia conductivitatii este data de , unde este parcursul mediu al undelor electrice în metal iar este impulsulelectronului aflat pe nivelul Fermi (nivelul energetic cel mai ridicat, ocupat de electroni la temperatura de zero absolut).

Pentru un fir de sectiune transversala si lungime o tensiune (diferenta de potential) aplicata la capetele sale produce (în metal) un câmp electric de intensitate .Aplicând legea lui Ohm în forma locala : , putem obtine intensitatea curentului: .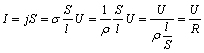

În aceasta expresie am notat cu , rezistenta electrica a firului metalic. Relatia se numeste legea lui Ohm pentru o portiune de circuit si arata proportionalitatea dintre intensitatea curentului si diferenta de potential.

Se poate arata ca un câmp de forte columbiene nu poate mentine un curent electric continuu într-un circuit. Aceasta se întâmpla deoarece fortele electrostatice conduc la redistribuirea sarcinilor electrice astfel încât câmpul electric în mediu conductor se anuleaza si potentialul ( sau ) devine acelasi peste tot.

Pentru a avea un curent continuu într-un circuit trebuie ca alaturi de fortele electrostatice sa actioneze asupra purtatorilor de sarcina liberi, forte de natura neelectrostatica numite forte exterioare .

Acestea sunt create de catre sursele de tensiune electromotoare (beterii electrice, acumulatoare, dinamuri,.) , care închid circuitul (recirculând sarcinile libere) si mentin constanta diferenta de potential dintre doua puncte oarecare ale circuitului.

Într-o sursa de tensiune electromotoare (t.e.m.) se consuma o energie de alta natura decât cea electrica (chimica, mecanica, termica, luminoasa,..)care transporta electronii de la borna minus la borna plus împotriva câmpului electric coulombian de la un potential mic la unul mai mare. Asupra electronilor actioneaza în interiorul sursei de t.e.m. forte exterioare iar în exteriorul sursei actioneaza forte electrice.

Asupra unui purtator de sarcina unitate actioneaza o forta:

unde este forta exteriora iar este forta coulombiana. Pentru o portiune de circuit de sectiune cuprinsa între punctele 1 si 2, lucrul mecanic efectuat pentru transportul unei sarcini unitate este :

,

unde :

,

: diferenta de potential în câmp electrostatic între punctele 1 si 2 , iar

este tensiunea electromotoare din portiunea de circuit cuprinsa între punctele 1si 2. T.e.m este gata cu lucrul efectuat de catre fortele exterioarapentru a transporta sarcina pozitiva unitate pe portiunea de circuit cuprinsa între punctele 1 si 2. Relatia anterioara devine :

.

4. Legi de conservare

4.1. Conservarea sarcini electrice

Din legea lui Gauss pentru câmpul electric : extragem :  si .

Din legea lui Ampere completata de Maxwell :   caruia îi aplicam operatorul , extragem :

( deoarece , produsul scalar a doi "vectori" perpendiculari fiind nul ) . Combinând cele doua relatii obtinem :

,

adica ecuatia de continuitate a sarcinii electrice.

4.2.Conservarea energiei în câmpul electromagnetic

Înmultim scalar cu si respectam cu ecuatiile :

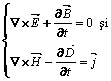
si le scadem membru cu membru :

.

Apoi aplicam identitatea : si obtinem :

În medie liniare avem cu si independente de timp , astfel încât . si .

Ecuatia anterioara capata forma :

Notam , vectorul Poynting si densitatea volumica de energie a câmpului electromagnetic, obtinând ecuatia de continuitate a energiei câmpului electromagnetic.

.

Integrând aceasta ecuatie pe n domeniu al spatiului tridimensional, semnificatia termenilor ei este urmatoarea : variatia de timp a energiei câmpului e.m. din acel domeniu se datoreaza fluxului de energie (vectorul Poznting) care strabate peretii domeniului ( al doilea termen ) si lucrului mecanic efectuat de catre câmpul electric asupra curentilor în unitatea de timp .

4.3. Conservarea impulsului în câmpul electromagnetic în vid

Forta exercitata de catre câmpul electromagnetic asupra sarcinilor si curentilor este :

.

Densitatea de forta si ) are expresia :

.

Vom elimina si din legea lui Gauss pentru câmpul electric si legea lui Ampere completata de Maxwell ( si )

Vom adauga ecuatiei termenul nul :

,

obtinând :

Notam , vectorul Poynting si , densitatea volumica de energie a câmpului electromagnetic, obtinând ecuatie de continuitate a energiei câmpului electromagnetic :

Integrând aceasta ecuatie pe un domeniu al spatiului tridimensional, semnificatia termenilor ei este urmatoarea: variatia în timpa energiei câmpului din acel domeniu se datoreaza fluxul de energie (vectorul Poynting) care strabate peretii domeniului (al doilea termen) si lucrul mecanic efectuat de catre câmpul electric asupra curentilor în unitatea de timp ().

4.3. Conservarea impulsului în câmpul electromagnetic in vid.

Forta exercitata de catre câmpul electromagnetic asupra sarcinilor si curentilor este :

.

Densitatea de forta () are expresia :

.

Vom elimina si din legea lui Gauss pentru câmpul electric si din legea lui Ampere completata de Maxwell ( si ) :

Vom adauga ecuatiei termenul nul :

,

obtinând :

Notam : , unde am considerat ca în vid si si .

Relatia precedenta devine : 

Vom trece la notatia tensoriala, aplicând regula de sumare a indicilor muti ai lui Einstein ca în exemplele urmatoare :

,

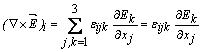, unde este tensorul Levi-Civita

1, când se ajunge la dupa un numar de permutari pornind

de la 123,0, când se repeta cal putin doi indici,

- 1,când se ajunge la dupa un numar impar de permutari

pornind de la 123.

Vom utiliza identitatile : si .

Sa calculam

În mod analog vom obtine :

Definim tensorul Maxwell al câmpului electromagnetic prin : si adica

:

tensiunea electromagnetica.

Cu aceste notatii, ecuatia de la care am pornit devine :

,

ecuatia de continuitate a impulsului.

este componenta a densitatii de impuls al câmpului electromagnetic. Variatia ei în timp se datoreaza fluxului de impuls prin peretii incintei si fortelor cu care câmpul actioneaza sarcinilor si curentilor.

Am vazut ca

În medii liniare si izolate unde si , cu si constante avem :

si .

4.4. Ecuatia de continuitate pentru momentul cinetic

Sa construim marimea tensoriala , este densitatea de impuls electromagnetic. Calculam densitatea la timp a acestei marimi: si luam în considerare ecuatia de continuitate a impulsului :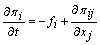

, unde am tinut seama de simetria 

a tensorului tensiune electromagnetica.

Relatia devine :

unde este densitatea de moment cinetic electromagnetic.

este componenta a densitatii de curent a momentului cinetic, relativ la transportul componentei a momentului cinetic, iar este densitatea de moment al fortei.

Ecuatia de continuitate a momentului cinetic capata forma :

.

5. Potentiale electromagnetice si transformari de etalon.

Ecuatia ofera posibilitatea construirii inductiei magnetice cu ajutorul potentialului vector :

,deoarece ,

Ecuatia : se transforma :

, unde este potentialul secundar, deoarece grad . Avem posibilitatea sa exprimam si câmpul electric cu ajutorul potentialelor vectoare :

Ecuatiile satisfacute de catre potentialele vectoare sunt :

.

si

.

Impunând potentialelor conditia de etalonare Lorentz : obtinem :

sau si

sau , unde este operatorul lui D Alembert .

Ecuatiile satisfacute de catre potentiale :

si ,

sunt ecuatiile de unda. Exista o infinitate de functii si

care conduc la aceleasi câmpuri .

Definitiile si nu fixeaza univoc potentialele si . De exemplu substituind , se obtine aceeasi valoare deoarece . Modificând potentialul scalar , obtinem aceeasi valoare a lui

. Cerând ca functiile si sa satisfaca etalonarea Lorentz :

, am obtinut ecuatia undelor, satisfacuta de functia .

Transformarile grad si lasa neschimbate câmpurile si si deci, ecuatiile lui Maxwell. Ele se numesc transformari de etalon.

5. Unde electromagnetice

5.1. Ecuatia undelor

Consideram un câmp electromagnetic în vid, în absenta sarcinilor electrice si a curentilor : , , si .

Scriem ecuatiile Maxwell :

si , pe componente, utilizând notatia tensoriala si regula de sumare a indicilor muti (indicii care se repeta) : si .

Derivam la timp cea dea doua ecuatie: si înlocuim derivata la timp din prima ecuatie :

,sau . Ne reamintim ca si obtinem:

Termeni 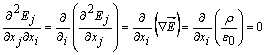se anuleaza deoarece .

Ecuatia, scrisa pentru componenta a câmpului devine :

sau , în forma vectoriala :

.

Vectorul satisface ecuatia undelor . Analog, derivând la timp prima ecuatie si tinând cont de derivata din cea de-a doua, obtinem ca si satisface ecuatia undelor :

Am vazut mai devreme ca si potentialele electromagnetice satisfac ecuatiei de acelasi tip : si .

O ecuatie de forma poarta numele de ecuatia undelor iar se numesc functia de unda . Solutia ecuatiei undelor este o expresie de forma: , unde este versorul directiei de propagare iar este viteza undei. Suprafata de-a lungul careia la un moment dat ia o anumita valoare, constanta, se numeste suprafata de unda la momentul . În cazul suprafetele de unda sunt plane cu normala comuna . Facem notatia astfel încât . Sa vedem în ce caz se obtine aceeasi valoare pentru , deci pentru :

distanta dintre suprafetele de unda la momentele si . Ultima expresie ne arata ca starile descrise de se propaga cu viteza în directia lui . Undele plane descrise de functia : .exp.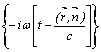

se numesc unde plane monocromatice. se numeste frecventa unghiulara , iar este vectorul de unda, fiind lungimea de unda iar amplitudinea undei. Cu aceste notatii, expresia undei plane monocromatice este : .

5.2. Proprietatile undelor electromagnetice

Notam , sau 1,2,3.

Potentialele si depind de timp si pozitie prin intermediul lui , deoarece satisface ecuatia undelor :

si .

a) Sa transcriem conditia Lorentz :

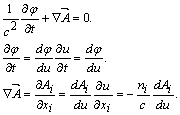
₍₁₎

b) Sa calculam , pe componenta :

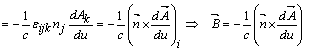(2)

c) Sa calculam pe componente :

, unde am tinut cont de relatia . De aici rezulta relatia vectoriala

(3)

unde am folosit identitatea

Din si obtinem :

(4)

Calculam , deoarece si din relatia , obtinem :

(5)

Comparând si rezulta ca într-o unda electromagnetica, vectorii si sunt reciproc perpendiculari.

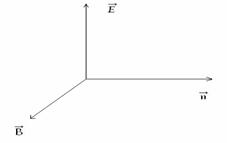
De asemenea , în marime si satisface relatia : .

d) În expresiile si ale câmpurilor si figureaza doar potentialul vectorul , nu si . Alergând , conditia Lorentz devine: . Relatiadevine:

Ţinând cont si de relatia : , calculam densitatea volumica de energie a câmpului electromagnetic :

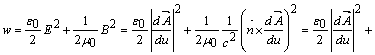
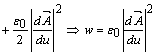. (6)

Vectorul lui Paynting se exprima :

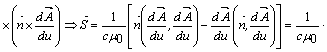
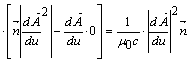
Deci , tinând seama de ecuatia , sau

. (7)

Densitatea de impuls capata forma :

. (8)

În cazul alegerii potentialului scalar nul , conditia Lorentz ne indica faptul ca variatia vectorului are loc planul perpendicular pe . Aceasta înseamna ca proiectia lui pe ramâne constanta si deoarece si se exprima doar în functie de variatia lui , vom face abstractie de aceasta componenta constanta, considerând vectorul complet situat în planul de unda (perpendicular pe ).