REGIMUL ELECTROSTATIC

Definire, caracterizare, legi si

teoreme specifice

Regimul electrostatic este regimul starilor electrice invariabile īn timp, neīnsotite de curenti electrici de conductie si de transformari energetice īn conductoare, fiind produs de sarcini electrice sau de distributii de sarcini electrice adevarate sau de polarizatie.

Caracteristice acestui regim sunt starile de electrizare si cele de polarizare electrica ale corpurilor izolatoare si existenta cāmpului electrostatic.

Se numeste stare de electrizare sau stare de īncarcare electrica adevarata a unui corp acea stare complet caracterizata de sarcina electrica libera, q, īn general multiplu al sarcinii elementare care este sarcina electronului.

Se numeste cāmp electrostatic cāmpul produs de o distributie de sarcini electrice aflate īn stare de repaus.

Din punct de vedere al actiunilor ponderomotoare (cupluri si forte) exercitate asupra unui mic corp de proba din material izolator (dielectric), polarizat, cāmpul electrostatic poate fi:

a. cāmp electrostatic omogen, īn care intensitatea sa, , nu depinde de pozitie, (r), si care actioneaza asupra corpului de proba numai prin cupluri;

b. cāmp electrostatic neomogen, care actioneaza asupra corpului de proba prin cupluri si forte.

Asa cum s-a aratat, īn cazul unui cāmp electrostatic omogen, vectorul cāmp electric nu depinde de distanta , fiind considerat constant īn toate punctele din cāmp, pe cānd īn cazul unui cāmp electrostatic neomogen, acesta depinde de (); practic un cāmp electric se poate considera omogen doar īntre armaturile foarte apropiate ale unui condensator electric.

Cum se poate evidentia starea de electrizare ?

Aceasta se poate pune īn evidenta introducānd īntr-un cāmp electric omogen un mic corp de proba electrizat, de exemplu, prin frecare sau prin contact.

Experienta arata ca asupra corpului se exercita o forta electrica independenta de pozitia corpului (r) si orientarea acestuia, avānd directia vectorului cāmp electric si fiind proportionala cu el:

Īn aceasta relatie factorul de proportionalitate q nu depinde de si nici de , aceasta definind starea de īncarcare electrica adevarata (starea de electrizare) a corpului de proba; q reprezinta sarcina electrica (adevarata) a corpului de proba si este, prin conventie, pozitiva sau negativa:

,

dupa cum si sunt omoparalele sau antiparalele.

Notiunea de stare de īncarcare electrica adevarata,doreste sa evidentieze faptul ca, īn afara de aceasta, mai exista o stare de electrizare si anume, electrizarea prin polarizare( a se vedea capitolul referitor la polarizare).

Starea de electrizare se poate obtine prin: frecare; contact; iradiere; introducerea corpului izolator īntr-un cāmp electric.

Īn afara marimii (primitive) q, sarcina electrica poate fi exprimata si cu ajutorul densitatilor de sarcina lineica, superficiala, volumetrica, , - marimi derivate.

Cāstigarea starii de electrizare poarta numele de īncarcare electrica, iar pierderea acesteia - descarcare electrica.

Din punct de vedere al modului de descarcare electrica se deosebesc:

a)           conductori electrici: metale, carbune, solutii de saruri organice, baze, acizi etc. - cu descarcare practic instantanee(relaxare electrostatica rapida);

b)          izolatori electrici(dielectrici): matase, mica, marmura, portelan, cauciuc, rasini sintetice, mase plastice, textolit, pertinax, aer uscat, uleiuri minerale, lemn, sticla, vid etc. - cu descarcare practic foarte lenta īn timp(relaxare īn timp īndelungat).

Astfel, conductoarele descarca prin contact corpurile electrizate, pe cānd izolantii nu-si schimba practic starea electrica īn contact cu corpurile de electrizate.

Pentru descarcarea unui corp electrizat , acesta se va pune īn contact cu un conductor, īn general de dimensiuni mai mari decāt acesta.

Conservarea sarcinii electrice

Sarcina totala a unui sistem de corpuri izolat este constanta:

Aceasta relatie este o consecinta ,pentru corpuri izolate electric, a legii conservarii sarcinii electrice ().

Conservarea sarcinii electrice poate fi evidentiata experimental īn doua situatii:

a) daca doua corpuri electrizate diferit vin īn contact, īncarcarea unuia se transmite partial si celuilalt, astfel īncāt sarcina totala ramāne constanta;

b) daca se freaca doua corpuri, dintre care unul se īncarca cu sarcina pozitiva iar celalat - negativa, valoarea absoluta a sarcinii totale ramāne constanta (frecarea nu aduce sarcini noi).

La frecarea a doua corpuri izolatoare, unul de celalalt, cel cu constanta dielectrica mai mare se īncarca pozitiv, iar celalalt negativ(regula lui Cohen).Densitatea sarcinii electrice superficiale este data de relatia:

(C/m²).

Interpretarea fizica a starii de electrizare

La nivel macroscopic starea de īncarcare electrica se defineste ca un exces sau un deficit de purtatori de sarcina electrica libera:

electroni, īn cazul metalelor;

electroni si goluri, īn cazul dielectricilor;

ioni pozitivi si negativi īn electroliti.

Īncarcarea sau descarcarea electrica a corpurilor este urmarea unui schimb de purtatori de sarcini electrice libere īntre acestea.

Unitati de masura. Rationalizarea

Unitatea de masura a sarcinii electrice este Coulombul(C). Un coulomb este sarcina unui mic corp conductor care exercita o forta de 9.10⁹N asupra unui alt corp conductor, īncarcat cu aceeasi cantitate de sarcina, situat īn vid la distanta de 1m si situat departe de alte corpuri (influente electrice).

Sistemul de unitati de masura utilizat este sistemul MKSA rationalizat, respecti 212h75c v sistemul international SI.

Rationalizarea a condus la disparitia factorului (sau ) din legile generale si ,ca urmare, la simplificarea acestora, cu pretul aparitiei acestui factor īn alte relatii mai putin generale (de exemplu īn teorema lui Coulomb).

Īn sistemul international se aleg:

- sistemul MKS ca sistem mecanic de baza;

- constanta k= 1(k= īn sisteme nerationalizate);

- amperul (A) ca unitate independenta, aceasta corespunzānd la alegerea lui ca marime fundamentala. Ca urmare, permitivitatea dielectrica a vidului ,, rezulta ca o marime derivata īn cadrul acestui sistem.

Exemplu - Definirea unitatii de sarcina electrica (Coulomb-ul) cu ajutorul teoremei lui Coulomb:

; k=1; ;

; ; rezulta: q=1 Coulomb.

Legi si teoreme specifice

Principalele legi si teoreme utilizate la studiul regimului electrostatic sunt:

- legea fluxului electric;

- legea polarizatiei electrice temporare;

- legea legaturii dintre ,si ;

- legea conservarii sarcinii electrice;

- legea echilibrului electrostatic (caz particular pentru regimul electrostatic al legii conductiei electrice);

- teorema lui Coulomb;

- teorema potentialului electrostatic;

- teorema conservarii componentelor tangentiale si respectiv normale ale cāmpului electric si ale inductiei electrice;

- teorema refractiei liniilor de cāmp electric la suprafata de separatie a doua medii;

- teorema energiei īn cāmpul electrostatic.

3.2. Cāmpul electric si potentialul electric coulombian

Un cāmp electric coulombian este acel cāmp electrostatic asociat unei repartitii de sarcina electrica, invariabila īn timp , ce se poate calcula cu ajutorul teoremei lui Coulomb. Īn continuare se studiaza cāmpurile coulombiene.

• Cāmpul electric produs de un mic corp de proba īn vid

Fie un mic corp de proba punctiform (un corp izolator, īnvelit īntr-o foita metalica) īncarcat cu sarcina electrica q.

Daca īn apropierea acestui corp se duce un mic corp de proba identic, īncarcat cu aceeasi cantitate de sarcina si de acelasi semn, īntre cele doua corpuri apar forte de interactiune prin cāmpul electric produs de acestea, care poate fi exprimat cu ajutorul formulei lui Coulomb, prezentata īn cap.2. :

.

Pe de alta parte, primul corp actioneaza asupra celui de al doilea, prin cāmpul sau, cu o forta data de relatia cunoscuta:

.

Din cele doua relatii, prin egalarea fortelor, rezulta expresia intensitatii cāmpului electric produs de un mic corp de proba īncarcat cu sarcina q īntr-un punct F , situat la distanta R de acesta, sub forma :

Daca se scrie , unde , relatia (3.2.1) se mai poate pune sub forma:

Pentru q>0 sensul cāmpului este īndreptat, prin conventie, dinspre corp spre exterior (fig. 3.2.1.a).

Pentru q<0 sensul cāmpului este īndreptat, prin conventie, dinspre exterior spre corpul de proba (fig. 3.2.1.b).

Se observa ca īn cazul corpului punctiform, distributia lui este radiala, cāmpul electric avānd aceleasi valori īn toate directiile, īn conditiile mediului īnconjurator omogen si izotrop.

Cum si sunt coliniare, pentru o directie intensitatea cāmpului electric devine o marime scalara:

Originea sistemului de coordonate carteziene care contine corpurile analizate poate sa nu fie īn punctul īn care se afla micul corp de proba īncarcat cu sarcina q (fig. 3.2.2).

Īntr-un punct oarecare , cāmpul electric se va calcula pornind de la componentele sale (E_x, E_y, E_z), tinānd cont de faptul ca:

; si , respectiv

.

Se obtin componentele:

Īn modul, intensitatea cāmpului electric este data de expresia:

Nota

La nivel microscopic, interactiile electrice se realizeaza prin intermediul fotonilor, care apar, ca particule de radiatie, īn jurul sarcinilor electrice. Acesti fotoni nu pot fi detectati, fiind numiti fotoni virtuali. Existenta lor a fost prevazuta, īnca din anul 1930, de Enrico Fermi, fiind pusi īn evidenta īn diagramele Feynman.

De studiul fenomenelor de interactiune a particulelor īn cāmpul electromagnetic se ocupa Electrodinamica Cuantica (QED).

Constanta care masoara intensitatea de cuplaj a doi electroni sau a doi protoni , respectiv energia lor electrostatica, acestia fiind situati la o distanta egala cu raza Bohr( m ) unul de celalalt, se numeste ''constanta de cuplaj electromagnetic'', , unde .

• Cāmpul electric produs de o sfera metalica īncarcata cu distributia superficiala de sarcina.

Se considera o sfera metalica de raza R si suprafata S, īncarcata cu distributia superficiala de sarcina fig.3.2.3).

Se pune problema determinarii intensitatii cāmpului electric īn punctele P₁ si P₂, aflate la distantele R_1, respectiv R₂ de centrul sferei, unde aceste distante au acelasi ordin de marime cu raza sferei.

Din motive de simetrie, liniile de cāmp sunt radiale. La calculul intensitatii cāmpului electric pentru corpuri cu simetrie sferica , cilindrica sau plana se poate utiliza teorema lui Gauss - un caz particular al legii fluxului electric:

Aceasta reprezinta expresia fluxului cāmpului electric printr-o suprafata īnchisa , ce contine o distributie superficiala de sarcina .

Īn cazul de fata si sunt omoparalele, suprafata fiind o suprafata sferica, concentrica cu sfera data si aflata la o distanta oarecare de centrul 0.

Ca urmare, se poate scrie:

Pe de alta parte, aplicānd teorema lui Gauss rezulta:

unde A reprezinta aria suprafetei sferei de raza r, īncarcata cu distributia de sarcina .

Din egalitatea celor doua relatii se obtine expresia intensitatii cāmpului electric , la o distanta oarecare de sfera data:

Particularizānd acum relatia pentru doua puncte, unul īn exterior si unul īn interior, se obtine:

Īn figura (3.2.4) se prezinta grafic variatia cu distanta r a cāmpului

S-a ales ca origine pentru reprezentarea grafica un punct pe suprafata sferei S.

Pe suprafata sferei cāmpul electric are valoarea constanta:

Se observa ca valoarea cāmpului electric īn interiorul unei sfere metalice (īn general īn interiorul unei suprafete metalice īnchise), este egala cu zero( indiferent daca sfera este plina sau goala).

Inductia electrostatica

Daca un baston de sticla īncarcat( prin frecare de o pānza de matase) cu sarcina electrica (pozitiva) este apropiat cu un capat de un baston de metal izolat (de alte corpuri metalice, sau de pamānt), se constata o deplasare a electronilor catre un capat al bastonului, miscarea acestora īncetānd apoi datorita fortei electrice rezultate care se stabileste īntre cele doua corpuri.

Este exemplul unui fenomen tipic de inductie prin cāmp electric (fig. 3.2.5).

Un astfel de fenomen se produce numai īn cazul corpurilor conductoare supuse cāmpurilor electrice, pe suprafata acestor corpuri apasānd sarcini opuse celor care produc cāmp electric inductor.

La īncetarea deplasarii purtatorilor de sarcina electrica (electroni), se restabileste īn conductor echilibrul electrostatic ().

Daca bastonul se īndeparteaza, conductorul revine la starea initiala (neutra, din punct de vedere electric).

Distributia sarcinilor electrice suplimentare depuse pe un conductor izolat

Cānd o sarcina electrica libera este depusa pe un conductor izolat, neīncarcat, īntr-un punct oarecare, aceasta sarcina va produce un cāmp electric īn interior care va actiona asupra purtatorilor de sarcina (electroni liberi), producānd deplasarea lor si deci dānd nastere unor curenti interni. Acesti curenti redistribuie sarcina suplimentara, astfel īncāt cāmpul intern creat slabeste īn intensitate īntr-un interval de timp neglijabil. Cānd cāmpul intern redevine zero, īnseamna ca īn interiorul conductorului curentii au īncetat si se revine la regimul electrostatic ().

Asadar, sarcina electrica adusa din exterior pe un conductor aflat īn regim electrostatic se distribuie instantaneu pe toata suprafata acestuia, conductorul revenind la conditia de echilibru electrostatic.

Superpozitia cāmpurilor coulombiene

Se constata experimental ca asupra unui mic corp de proba electrizat, care se gaseste simultan sub actiunea mai multor corpuri punctuale, īncarcate cu sarcini electrice , actioneaza o forta egala cu suma vectoriala a fortelor pe care le-ar exercita asupra corpului fiecare dintre corpurile punctuale, daca ar actiona singura asupra corpului de proba (fig. 3.2.6).

Acelasi lucru se poate afirma si despre cāmpul electric rezultant, , produs de un ansamblu de n corpuri punctuale īncarcate cu sarcina electrica, īntr-un punct oarecare P (nu se ia īn consideratie contributia corpului de proba, aflat chiar īn punctul P).

Demonstratie

Se stie ca fortele care se exercita de catre fiecare corp punctual asupra corpului de proba īncarcat cu sarcina sunt de forma:

; ,

unde reprezinta cāmpurile electrice produse īn punctul P de fiecare corp punctual , mediul considerat fiind vidul.

Ţinānd seama de faptul ca forta rezultanta īn punctul P se poate scrie sub forma:

si luānd īn consideratie expresia (3.2.12) se obtine, īnlocuind pe si respectiv pe , relatia:

respectiv

Vectorul intensitatea cāmpului electric īn vid, produs īntr-un punct P oarecare de un ansamblu de sarcini punctiforme este suma vectoriala a vectorilor cāmp electric produsi īn punctul P de fiecare corp punctual īn parte, ca si cum aceasta ar actiona singur īn sistem.

Ţinānd seama de expresia intensitatii cāmpului electric, relatia (3.2.15) se mai poate scrie:

S-ar putea spune ca vectorul caracterizeaza un cāmp electric (īn vid sau īntr-un mediu oarecare) īn sens longitudinal, pe cānd vectorul īl caracterizeaza īn sens transversal.

Cāmpuri electrice īn corpuri izolatoare (dielectrici)

Studiul cāmpului electrostatic īn corpuri (izolatoare) se bazeaza pe determinarea vectorilor si respectiv īn doua fante īnguste si scurte, practicate īn aceste corpuri (fig. 3.3.7 a si b).

Astfel intensitatea cāmpului electric īntr-un punct din corp este egala numeric cu vectorul cāmp din vidul unui mic canal orientat īn lungul directiei polarizatiei electrice , iar inductia electrica īntr-un punct dintr-un corp este o marime de stare locala a cāmpului electric, egala numeric cu produsul dintre si vectorul cāmp din vidul unei mici fante, extrem de plate, orientate transversal fata de directia locala a polarizatiei electrice .

Potentialul electrostatic

Asa dupa cum s-a aratat la teorema potentialului electrostatic (forma integrala: ), cāmpul electric coulombian este un cāmp de vectori pentru care se poate defini o functie scalara de punct V prin relatia:

deoarece produsul este, īn acest caz, o diferentiala totala.

Functia poarta numele de potentialul scalar al cāmpului electrostatic si are forma: .

Relatia (3.2.17) se mai poate scrie :

sau

unde

,

iar

.

Expresia: 

reprezinta forma locala a teoremei potentialului electrostatic, iar expresia

- forma integrala a acesteia,

Alte moduri de scriere ale relatiei (3.2.17')sunt:

cu operatorul Nabla: ,

respectiv

Cāmpul electric coulombian are rotorul nul īn orice punct al domeniului analizat deoarece deriva dintr-un potential scalar V.

Expresia potentialului electrostatic īn cāmp coulombian

Pornind de la relatia (3.2.17')si integrānd-o īn lungul unei curbe (C) oarecare īn cāmp electrostatic, īntre doua puncte (fig 3.2.8), se obtine:

de unde: 

sau

este potentialul īntr-un punct oarecare P, iar este potentialul unui punct de referinta P_o, care se considera, īn mod obisnuit, pe pamānt, la distanta mare de punctul P (). Cum potentialul pamāntului este, prin conventie, nul, si expresia potentialului electric coulombian īntr-un punct oarecare P din cāmpul electrostatic īn vid devine:

Aceasta relatie arata ca potentialul este egal cu viteza de scadere a intensitatii cāmpului electric fata de punctul īn care se calculeaza acesta, luāndu-se ca potential de referinta potentialul (nul) al pamāntului.

Īn cazul particular al cāmpului electric produs īn vid de un corp punctiform īncarcat cu sarcina q, a carui expresie este :

forma expresiei potentialului electrostatic devine:

Cum īn acest caz , prin integrare rezulta:

Convenind alegerea potentialului de referinta nul la infinit, constanta este nula si rezulta:

Suprafete echipotentiale

Se numesc suprafete echipotentiale suprafetele caracterizate de ecuatia:

Īn raport cu liniile cāmpului electric , suprafetele echipotentiale sunt ortogonale.

Astfel, din relatia , valabila pentru orice curba īnchisa īn cāmpul electric, deci si pentru curbele īnchise duse pe suprafetele echipotentiale, scrisa sub forma:

, rezulta ortogonalitatea vectorilor (continut de suprafata echipotentiala si grad (fig. 3.2.9)).

Liniile de cāmp sunt, deci, normale la suprafetele echipotentiale.

Īn sensul vectorului cāmp potentialul scade.

Din relatia se poate trage concluzia ca vectorul este mai intens īn zone unde suprafetele echipotentiale sunt mai apropiate, adica este mai mic si invers.

Calculul tensiunii electrice cu ajutorul potentialului

Tensiunea electrica dintre doua puncte si aflate īn cāmp electrostatic are expresia (fig. 3.2.10):

Tensiunea electrica īntre doua puncte situate īn cāmpul electrostatic este egala cu diferenta potentialelor electrice ale celor doua puncte.

Potentialul īntr-un punct al cāmpului electrostatic dat de un ansamblu de corpuri punctuale īncarcate

Īn cazul unui ansamblu de corpuri punctuale, īncarcate cu sarcinile , utilizānd principiul superpozitiei se poate scrie:

unde sunt distantele de la corpuri la punctul , potentialul de referinta fiind potentialul pamāntului (). Īn cazul unui corp cu distributie variata de sarcina: volumetrica, superficiala, lineica si sarcina electrica libera, potentialul īntr-un punct exterior, aflat la distanta medie geometrica (- a se vedea īn acest sens relatiile lui MAXWELL) fata de corp este:

potentialul de referinta fiind de asemenea egal cu zero.

Potentialul si cāmpul electrostatic īn interiorul conductoarelor omogene, īn regim electrostatic

Din conditia de echilibru electrostatic , cum este nul rezulta ca īn interiorul conductoarelor omogene aflate īn regim electrostatic (neparcurse de curent de conductie) cāmpul electric (fig. 3.2.11).

Din relatia rezulta ca , adica toate punctele din interiorul conductoarelor aflate īn regim electrostatic au acelasi potential ().

Sarcina electrica libera din interiorul suprafetei conductorului are rezultanta nula, existānd o distributie de sarcina numai la suprafata conductorului (la interfata cu aerul presiunea, temperatura, diferenta de densitate variaza de la un mediu la altul).

Unitatea de masura a potentialului electrostatic īn SI este

[V]=1V (Volt).

Introducerea notiunii de potential. Interpretare fizica

Conceptul de potential a fost indus īn fizica de Isac Newton pentru explicarea atractiei dintre corpuri. Functia potential este introdusa īn matematici de Gauss, īn 1840, relativ la suprafetele echipotentiale.

Interpretare fizica : Potentialul electric īntr-un punct oarecare P din cāmpul electrostatic reprezinta lucrul mecanic efectuat pentru a deplasa un corp punctiform de sarcina q īn cāmp electric, īntre punctul si punctul curent P:

Demonstratie:

Lucrul mecanic cheltuit pentru a efectua o astfel de deplasare este dat de relatia:

Lucrul mecanic este luat cu sensul minus, deoarece acesta se considera ca este opus fortei cāmpului īn care se face experienta. Din expresia lucrului mecanic se obtine expresia potentialului:

Conditia de echilibru electrostatic

Starea de echilibru electrostatic este starea de anulare a miscarii ordonate a particulelor īn conductoare, fiind caracterizata prin relatia:

Aceasta relatie reprezinta un caz particular al legii conductiei electrice (), valabila īn cazul īn care densitatea de curent este nula( ).

Marimea poarta numele de cāmp electric imprimat si apare īn conductoare ca o consecinta, exprimata electric , a fenomenelor neelectrice produse asupra acestora (acceleratii, diferente de temperatura, diferente de presiune etc.); este o marime electrica de material.

Din relatia (3.2.31) rezulta , relatie care arata ca, la atingerea starii de echilibru electrostatic, valoarea pe care o ia intensitatea cāmpului electric īntr-un conductor neomogen sau accelerat este valoarea intensitatii cāmpului electric imprimat, luata cu semnul minus.

Īn cazul conductoarelor omogene si neaccelerate si, ca urmare, conditia de echilibru electrostatic, īn orice punct din interiorul acestora, devine . Aceasta relatie are cāteva consecinte deosebit de importante si anume:

a. Toate punctele din interiorul unui conductor au aceslasi potential.

Astfel, din rezulta ca īntre oricare doua puncte din interior este īndeplinita relatia:

ca urmare, , respectiv .

b.      Suprafata conductorului este echipotentiala.

Liniile de cāmp electric la suprafata conductorului sunt perpendiculare pe aceasta suprafata (demonstratia se bazeaza pe cele aratate la punctul a.).

c. Sarcina electrica din interiorul conductorului este nula. Exista o distributie slaba de sarcina la suprafata conductorului, unde se schimba conditiile de temperatura, presiune etc.

d. Liniile de cāmp electric din exteriorul unui conductor nu patrund īn interiorul unui gol din conductor. Astfel, conductorul are rol de ecran electrostatic.

3.3. Polarizarea dielectricilor

Starea de īncarcare cu sarcina electrica adevarata nu este singura stare de electrizare, o alta fiind polarizarea dielectricilor (materiale izolatoare).

Se numeste stare de polarizare electrica acea stare a corpurilor izolatoare care determina exercitarea asupra lor a unor forte si cupluri electrice suplimentare fata de cele conditionate de eventuala lor stare de īncarcare electrica, atunci cānd sunt introduse īn cāmpuri electrice.

Identificarea starii de polarizare

Īn cāmpuri electrice omogene ( nu depinde de ) , un mic corp de proba polarizat electric este supus numai unui cuplu, forta de interactiune fiind egala cu zero.

Acest lucru poate fi evidentiat prin urmatoarea experienta: se aduc īn apropierea unui corp electrizat (īncarcat cu sarcina adevarata) mici corpuri izolatoare, foarte usoare (mici bucatele de hārtie), neīncarcate cu sarcini electrice; acestea vor fi atrase de corpul electrizat, desi initial nu erau īncarcate electric. Concluzia care se poate trage de aici este aceea ca aceste corpuri s-au polarizat sub actiunea cāmpului electric al corpului electrizat, īntre ele si corpul electrizat aparānd interactiuni sub forma de cupluri.

Asadar, un corp este polarizat electric daca produce cāmp electric si este supus unor actiuni ponderomotoare īn cāmp electric exterior, fara a avea densitatea de sarcina electrica libera.

O comparatie īntre modurile de manifestare īn cāmp electric a corpurilor electrizate si a celor polarizate este prezentata mai jos:

a)corp electrizat īn cāmp electric omogen:

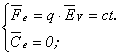
b)corp electrizat īn cāmp electric neomogen:

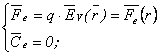
c)corp polarizat īn cāmp electric omogen:

d)corp polarizat īn cāmp electric neomogen: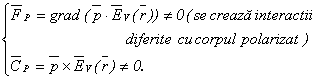

Observatie

Cāmpul electric omogen este acela īn care nu depinde de distanta r ( = const.), īn cāmp electric neomogen intensitatea cāmpului electric fiind o functie de distanta ().

Se poate vorbi de polarizare electrica numai īn cazul corpurilor izolatoare; metalele sunt practic nepolarizabile electric.

Caracterizarea starii de polarizare electrica

Starea unui corp mic de proba polarizat se caracterizeaza complet prin momentul electric (C.m). Starea unui corp izolator polarizat de dimensiuni mai mari se caracterizeaza, īn fiecare punct ,prin vectorul polarizatia . Asadar, este un vector de punct.

Polarizatia corpurilor poate fi temporara sau permanenta.

Majoritatea materialelor izolatoare se polarizeaza temporar, respectiv se conformeaza legii polarizatiei temporare , atunci cānd sunt introduse īntr-un cāmp electric.

Cauzele polarizarii permanente sunt:

-deformarea mecanica a unor cristale (avānd drept consecinta efectul piezoelectric, de pilda);

-īncalzirea unor cristale;

- introducerea unor rasini, ceruri sau a plexiglasului, aflate īn stare topita, īntr-un cāmp electric exterior intens, urmata de o racire lenta īn cāmp.

Cele mai cunoscute materiale cu polarizatie permanenta sunt cristalele de cuart (se utilizeaza, de pilda , la realizarea de doze piezoelectrice).

Exista si un proces fizic invers efectului piezoelectric: prin excitarea pe doua fete opuse a unui cristal de cuart cu o tensiune alternativa de o anumita frecventa, cristalul capata deformari elastice; fenomen fiind utilizat la etaloanele de frecventa, la generatoarele de ultrasunete, la ceasurile cu cuart s.a.

Echivalenta unui mic corp polarizat cu un dipol electric

Avānd īn vedere faptul ca moleculele unui corp izolator sunt neutre din punct de vedere electric, studiul fenomenelor electrice care au loc īn interiorul corpului polarizat se poate face, la nivel macroscopic, studiind sarcina de dipol.

Se numeste dipol electric un sistem de doua sarcini electrice punctuale, egale si de semne contrare(q, -q), situate la distanta l una fata de alta (), astfel īncāt produsul este finit (fig. 3.3.1).

Se defineste un moment al dipolului (+q,-q):

unde , iar pentru ca produsul () sa fie finit (a se vedea definitia dipolului).

Fortele care actioneaza asupra dipolului electric sunt date de relatia:

Teorema echivalentei

Īn regim electrostatic, un mic corp polarizat de moment electric este echivalent cu un dipol electric de moment , din doua puncte de vedere:

a)      al cāmpului electric produs de el īn vid;

b)      al actiunilor ponderomotoare (cupluri si forte) exercitate asupra lui de un cāmp electric exterior.

Presupunānd cāmpul omogen (fig. 3.3.1), se observa ca forta si cuplul exercitate de acesta asupra dipolului sunt echivalente cu cele exercitate asupra unui mic corp izolator:

Cuplul are o expresie similara cuplului , al corpului de proba polarizat:

Forta rezultanta supra dipolului introdus īn cāmp electric are aceeasi valoare cu forta - asupra corpului de proba polarizat:

Teorema este demonstrata.

Studiul comportamentului unui corp polarizat cu ajutorul dipolului electric este comoda, considerānd,īn teoria macroscopica, sarcinile dipolare ca marimi fictive, de calcul (la scara atomica, sarcinile dipolare au corespondent īn sarcinile microscopice din atomi).

Interpretarea macroscopica a polarizatiei electrice

Īn natura corpurile sunt īn mod normal neutre din punct de vedere electric, continānd particule cu sarcini pozitive si negative īn mod egal.

Se va considera, ca exemplu, un atom de hidrogen simplu (fig. 3.3.2, a si b).

Īn absenta unui cāmp electric exterior, momentul electric mijlociu, corespunzator sarcinilor electrice (+q = proton si -q = electron) este nul (fig.3.3.2. a):

Momentul electric mijlociu se defineste īn conditiile rotatiei electronului īn jurul protonului.

Introducānd atomul de hidrogen īntr-un cāmp exterior, are loc fenomenul de polarizare, purtatorii de sarcini electrice deplasāndu-se putin (), īn sensul cāmpului (protonii) si īn sens opus (electronii) (fig.3.3.2. b):

.

Se produce, astfel, o polarizare a atomului de ,prin deformare cvasielastica.

Corpurile izolatoare la care predomina polarizatia prin deformare se numesc corpuri dielectrice (pe scurt, dielectrici), iar cele la care predomina polarizarea prin orientare se numesc corpuri paraelectrice. Corpurile dielectrice sunt predominante īn tehnica. Atāt corpurile dielectrice cāt si cele paraelectrice sunt corpuri care se polarizeaza temporar.

Potentialul si cāmpul electric al unui mic corp polarizat

Pe baza masuratorilor experimentale si a calculelor s-a putut demonstra ca īn cazul corpurilor polarizate cāmpul electric scade cu distanta la puterea a treia, iar potentialul - la puterea a doua, pe masura īndepartarii de aceaste corpuri:

Mai mult, cāmpul produs de un corp polarizat depinde nu numai de distanta, ci si de directia razei vectoare, , fiind un cāmp electric neomogen (fig. 3.3.2).

Sub actiunea cāmpului electric, corpurile izolatoare se polarizeaza, fiecare element de volum devenind un dipol electric ().

Pentru dielectrici (izolatori) , depinde de cāmpul exterior, , dar si de valorile lui anterioare. Acesta dependenta de valorile anterioare se manifesta printr-o īntārziere a procesului de polarizare fata de evolutia cāmpului electric si poarta numele de histerezis dielectric:

.

Rezulta, de fapt, o īntārziere a vectorului fata de cāmpul polarizant .

Se poate introduce notiunea de polarizabilitate atomica ,, care caracterizeaza atomul din punct de vedere al deformarii sale elastice īn cāmp electric:

Rigiditatea dielectrica

Proprietatea de izolant a unui corp se poate pierde daca intensitatea cāmpului electric exterior, īn care este introdus, depaseste o anumita valoare limita , numita rigiditate dielectrica(E_d). Aceasta marime depinde de caracteristicile corpului, precum si de temperatura si presiunea mediului īnconjurator.

Cāteva valori ale rigiditatii dielectrice si ale permitivitatii dielectrice relative (dupa Manualul inginerului electrician - SIEMENS) sunt date īn tabelul urmator:

Observatie

Īn practica se ia pentru aer ; deci relatiile electrostaticii se pot scrie ,īn aer ca si īn vid:

.

3.4. Capacitatea electrica. Condensatoare electrice.

Calculul capacitatii unui condensator. Protectia

la descarcarea condensatoarelor

Se considera un sistem de doua conductoare omogene din acelasi material, īncarcate cu sarcinile si , īntre care se afla un dielectric omogen, avānd permitivitatea relativa .

Cele doua conductoare sunt mentinute la potentialele , respectiv .

Raportul, īntotdeauna pozitiv:

se numeste capacitate electrica (fig. 3.4.1).

Un astfel de sistem poarta numele de condensator electric si se noteaza simbolic īn schemele electrice cu C.

Pentru a arata ca īn cazul unui condensator electric , se aplica legea fluxului electric unei suprafete īnchise ce trece prin atmaturile condensatorului si prin aer:

Integrala este identic nula deoarece, descompunānd suprafata īn suprafete laterale si suprafete prin armaturi, īn primul caz (īn aer), iar īn cel de-al doilea (īn armaturi , respectiv sunt nule). Astfel spus, īn dielectric, deci īn interiorul suprafetei , este nula si corespunzator .

Dar : 

deci:

Unitatea de masura pentru capacitatea electrica este Faradul:[C] =1 F (Farad), unde :   .

Submultipli frecvent utilizati sunt:

; ; .

Pentru a avea o idee asupra marimii capacitatii unui condensator electric se dau trei exemple simple:

Exemplul 1. Capacitatea unui condensator plan format din doua armaturi, avānd suprafata de 100 cm² (10 x 10 cm) fiecare, situate la distanta d = 1mm, īntre placi fiind aer, este de 88,33 pF.

Exemplul 2. Capacitatea unui condensator plan format din doua armaturi avānd suprafata de 100 Km² (10 x 10 Km) fiecare, situate la distanta d = 1 mm, īn aer, este de 1F.

Exemplul 3. Capacitatea pamāntului, considerat drept condensator sferic, este de circa 5F.

Teorema capacitatii electrice

Capacitatea unui condensator liniar (īn sensul ca dielectricul este liniar, respectiv este ct. si nu depinde de E) este independenta de q si de , depinzānd numai de raportul acestora; capacitatea este o caracteristica de material si de geometria condensatorului (fig. 3.4.2).

Din rezulta ; aceasta este ecuatia unei drepte prin originea sistemului de coordonate (). Īn aceste conditii se poate scrie relatia:

,

unde k este factorul de scara, (), iar este unghiul pe care īl face dreapta cu abscisa.

Calculul capacitatii unui condensator

Pentru calculul capacitatii unui condensator electric se fac urmatoarele ipoteze:

a. Se presupune condensatorul īncarcat cu sarcinile .

b. Se determina intensitatea cāmpului electric dintre armaturi.

c. Se calculeaza potentialele armaturilor, respectiv diferenta de potential dintre acestea (tensiunea electrica īntre cele doua borne ale condensatorului).

d. Se calculeaza capacitatea condensatorului.

Exemplu. Calculul capacitatii unui condensator plan.

Se considera condensatorul plan din fig. 3.4.3.

Dielectricul se considera omogen si izotrop, avānd permitivitatea ; d - distanta dintre armaturi - este mult mai mica īn raport cu lungimea armaturii.

Se duce o suprafata īnchisa prin armatura pozitiva a condensatorului si prin dielectric, aceasta suprafata avānd aria laterala perpendiculara pe liniile de cāmp. Aria armaturii condensatorului este A. Se vor urma, pentru calculul capacitatii, etapele aratate mai sus.

a.       Se presupune condensatorul īncarcat cu sarcinile +q si -q.

b.      Pentru determinarea intensitatii cāmpului electric se aplica legea fluxului electric suprafetei elementare īnchise :

deoarece si sunt omoparalele pe fata laterala inferioara a lui , iar suprafata contine īn interior sarcina ; .

Ca urmare, se poate scrie:

sau, extinzānd la īntreaga suprafata a armaturii:

sarcina fiind uniform repartizata pe suprafata armaturii .

Pe de alta parte, dielectricul fiind considerat liniar i se poate aplica relatia , respectiv , cei doi vectori fiind omoparaleli.

Īn aceste conditii se poate calcula E:

c. Calculul tensiunii īntre armaturi se poate face acest īn acest caz utilizānd relatia:

Pentru aceasta s-a considerat ca originea sistemului de coordonate este pe armatura 1, cāmpul dezvoltāndu-se dupa directia O_x. Īnlocuind pe E cu rel (3.4.8) rezulta:

d. Capacitatea condensatorului plan devine īn acest caz:

Teoremele capacitatilor echivalente

Se numeste capacitate echivalenta marimea , data de expresia:

īn care A si B sunt bornele de acces ale condensatorului echivalent.

a . Capacitatea echivalenta a condensatoarelor legate īn paralel (fig. 3.4.4)

Īn acest caz, sarcina totala este de forma:

Condensatorul echivalent cu care se poate īnlocui ansamblul paralel are capacitatea:

tensiunea la bornele celor n condensatoare īn paralel fiind aceeasi ().

Cum ; s.a.m.d., rezulta ca:

Capacitatea echivalenta a unor condensatoare conectate īn paralel este suma capacitatilor acestor condensatoare.

c.       Capacitatea echivalenta a condensatoarelor legate īn serie (fig. 3.4.5)

Īn acest caz sarcina electrica este aceeasi pentru toate condensatoarele, īnsa tensiunea electrica se repartizeaza pe fiecare condensator astfel:

Cum:

rezulta:

Īnlocuind īn relatia (3.4.15) ,se obtine:

Pe de alta parte, ansamblul de condensatoare serie poate fi īnlocuit cu capacitatea echivalenta:

Din egalitatea relatiilor (3.4.16) si (3.4.17) se obtine:

relatie pe baza careia se calculeaza

Īncarcarea unui condensator

Fie un circuit de c.c. care contine o sursa de c.c., E, rezistenta R si condensatorul C. Se va analiza procesul de īncarcare al condensatorului, īncepānd din momentul īnchiderii īntrerupatorului K.

Ecuatia circuitului īn momentul īnchiderii īntrerupatorului K(t=0) este:

Regimul de īncarcare este un regim variabil (tranzitoriu), asfel ca marimile de stare, si,, sunt variabile īn timp pe īntreaga durata a acestui proces.

Se aplica legea conservarii sarcinii electrice( pentru cazul īncarcarii unui condensator):

care īn cazul de fata devine:

Se vede ca pe durata īncarcarii condensatorului sarcina electrica de pe armaturi creste continuu (mai departe se va vedea ca aceasta crestere este exponentiala).

Ecuatia (3.4.18.) devine:

deoarece , conform teoremei condensatorului, .

Solutia ecuatiei diferentiale neomogene este :

unde:

- solutia de regim liber, regim care are loc doar pe durata īncarcarii condensatorului;

- solutia de regim fortat sau permanent, valabila dupa trecerea regimului tranzitoriu, reprezentānd sarcina maxima la care se īncarca condensatorul si cu care se calculeaza capacitatea acestuia.

Solutia de regim liber este solutia ecuatiei diferentiale omogene:

Pentru obtinerea acesteia se rezolva ecuatia caracteristica:

obtinānd . Ca urmare, solutia ecuatiei (3.4.21.) devine :

unde solutia de regim permanent este:

si reprezinta cantitatea de sarcina pe fiecare armatura (evident , cu semnele plus si minus) cānd condensatorul este īncarcat.

Determinarea constantei A se face punānd conditia initiala privitoare la asigurarea , pe considerente fizice, a continuitatii sarcinii sarcinii pe armaturile condensatorului īn momentul īnchiderii īntrerupatorului, deci īn momentul ( ca o consecinta a legii conservarii sarcinii electrice):

Cu alte cuvinte sarcina dinaintea īnchiderii īntrerupatorului, respectiv din momentul () tinde sa ramāna nemodificata pentru un interval de timp foarte scurt () , pe durata īnchiderii īntrerupatorului, pāna la momentul () . Este vorba de conditii initiale nule.

Acelasi lucru se poate spune despre tensiunea de la bornele condensatorului. Ca urmare , īn conditii initiale nule se poate scrie:

sau:

de unde rezulta ca .

Asadar solutia ecuatiei (3.4.21.) devine:

unde, asa cum s-a aratat, solutia de regim permanent este:

Relatia (3.4.3.1.) reprezinta teorema capacitatii, valabila dupa īncarcarea condensatorului , cānd nu mai circula curent prin circuit si .

Īn continuare se poate scrie:

relatie care arata modul de evolutie al sarcinii pe armaturile condensatorului pe durata procesului de īncarcare si din care se pot deduce si cazurile pentru , respectiv .

Concluzii

1. Pe toata durata īncarcarii condensatorului (durata regimului liber , tranzitoriu) sarcina creste pe armaturile acestuia de la

2. Tensiunea la bornele condensatorului creste si ea conform relatiei :

La terminarea īncarcarii (teoretic la ) , tensiunea devine:

expresie obtinuta din rel. anterioara pentru .

3. Capacitatea condensatorului creste si ea pe durata īncarcarii , de la valoarea

la pentru (teoretic). Practic, īncarcarea completa se atinge dupa un interval de timp unde reprezinta constanta de timp a circuitului.

Determinarea grafica a acestei constante este evidentiata īn figura 4.5.7.

4. Variatia curentului prin circuit se obtine din legea conservarii sarcinii electrice ( pentru cazul īncarcarii condensatorului):

Graficul evolutiei tensiunii la bornele condensatorului si a curentului ( de deplasare) prin condensator, īn valori normate, pe durata īncarcarii acestuia, sunt prezentate īn figura 4.5.7. a si b. Graficul evolutiei sarcinii este asemanator celui al evolutiei tensiunii la bornele condensatorului, la o alta scara.

Constanta de timp a circuitului, , se determina grafic prin ducerea tangentelor la cele doua curbe īn origine. Se observa din cele doua grafice ca īncarcarea completa se atinge dupa un interval de timp .

Cresterea capacitatii unui condensator

Vom presupune acum ca īntre armaturile unui condensator, al carui dielectric era initial aerul (), se introduce un alt dielectric cu permitivitatea relativa . Īn asemenea conditii, se poate arata cum capacitatea condensatorului creste de ori:

Ca urmare, raportul celor doua capacitati devine:

Se pune īntrebarea : cum se explica aceasta crestere?

Se va presupune ca condensatorul ramāne conectat la sursa de alimentare ( acumulator sau retea). Cāmpul electric dintre armaturi dupa introducerea noului dielectric , avānd , va avea expresia:

unde :

cāmpul dintre armaturi īn prezenta dielectricului aer;

cāmpul de polarizatie din noul dielectric (altul decāt aerul);

Cele doua cāmpuri sunt prezentate īn figura 3.4.8.a. si b.

Condensatorul ramānānd conectat la sursa de alimentare, potentialele celor doua armaturi ramān constante si , ca urmare, tensiunile la borne:

unde:

- tensiunea la bornele condensatorului cu aer;

- tensiunea la bornele condensatorului cu noul dielectric.

Din relatia (3.4.41.) rezulta ca īn aceste conditii :

Conform relatiei (3.4.40.), cāmpul electric dintre armaturile condensatorului cu noul dielectric tinde sa scada datorita lui . Acest lucru nu este īnsa posibil deoarece condensatorul, conform ipotezei initiale, a ramas conectat la sursa, iar aceasta forteaza egalitatea (3.4.42.). La introducerea noului dielectric capacitatea condensatorului creste de ori si cum ( īn cazul de fata , unde este t.e.m. a sursei), daca cresterea capacitatii se datoreaza cresterii cantitatii de sarcini pe armaturi (sursa trimite noi sarcini).

Energia electrostatica a unui condensator

Energia electrostatica a unui condensator este acumulata īn dielectricul acestuia si poate fi calculata, de pilda, prin sumarea lucrurilor mecanice elementare efectuate pentru transportul de sarcina elementara de la o armatura la alta:

Rezulta:

Se poate calcula si densitatea de energie īnmagazinata īn dielectric:

unde V este volumul dielectricului.

Cunoscānd ca:

unde:

A - aria armaturii condensatorului;

d - distanta dintre armaturi;

E - cāmpul electric dintre armaturi _,

rezulta:

Energie si forte īn cāmpul electrostatic

Energia electrostatica a unui sistem de conductoare

Pentru a stabili un cāmp electromagnetic īntr-o regiune din spatiu este necesar a fi efectuat un lucru mecanic exterior (se aplica primul principiu al termodinamicii, fiind vorba de o schimbare de stare).

Se considera un sistem de n corpuri conductoare, initial neīncarcate cu sarcini electrice, sistemul fiind izolat fata de alte sisteme sau corpuri din mediu. Se īncarca treptat cu sarcini electrice aduse dintr-un punct exterior , aflat la infinit, cele n conductoare ale sistemului. Energia cāmpului electrostatic care se stabileste īn final, cānd corpurile au fost īncarcate, este egala cu lucrul mecanic total efectuat de fortele exterioare pentru a īncarca cele n corpuri, initial neīncarcate (Fig. 3.5.1.).

Īn continuare va fi determinata expresia acestei energii.

Transportul sarcinilor electrice pentru īncarcarea fiecaruia din cele n corpuri se face cu ajutorul unui mic corp de proba, deci īn portii infinitezimale, astfel īncāt, la un moment, dat sarcina electrica pe un conductor oarecare k reprezinta o fractiune din valoarea ei finala pe acel conductor. Fie sarcina electrica la un moment dat pe conductorul k. Pentru deplasarea micului corp de proba de la pāna la corpul k, trebuie utilizata o forta:

egala si opusa celei exercitate de sarcina , depusa deja pe conductoare pāna īn momentul respectiv.

Lucrul mecanic al acestei forte pe traseul () este:

iar lucrul mecanic efectuat la un astfel de transport pentru toate corpurile devine:

Avānd īn vedere ca la un moment dat teorema potentialului electrostatic sub forma locala () se mai poate scrie:

cu (punctul fiind luat pe pamānt), va rezulta ca lucrul mecanic elementar la un transport pentru toate cele n corpuri se poate scrie sub forma:

Starile intermediare ale procesului de electrizare pot fi redate cu ajutorul unei variabile de stare, , unde ,astfel:

astfel īncāt devine:

Cum energia acumulata de cāmpul electric care se creaza este egala cu lucrul mecanic consumat pentru producerea acesteia, relatia (3.5.5) devine:

de unde:

Prin integrare rezulta expresia finala a energiei acumulate īn cāmpul electric al celor n conductoare:

Se poate defini si o densitate de energie pe unitatea de volum sub forma:

astfel īncāt:

O alta forma a energiei cāmpului electrostatic este data de relatia:

unde:

Exemplu

Energia cāmpului electrostatic īn dielectricul unui condensator electric īncarcat (sistem format īn acest caz numai din doua corpuri conductoare) este:

deoarece si .

Cum este tensiunea la bornele condensatorului, energia cāmpului devine:

Ţinānd seama ca , expresia energiei mai poate fi scrisa sub forma:

Teoremele fortelor generalizate īn cāmpul electrostatic

Fortele care se exercita asupra corpurilor electrizate, situate īn cāmpul electrostatic, nu se pot calcula īntotdeauna cu relatia lui Coulomb din urmatoarele motive:

- relatia lui Coulomb este valabila numai pentru dielectricii omogeni;

- la un numar mai mare de corpuri, utilizarea acestei relatii devine incomoda.

Ca urmare, s-a trecut la elaborarea unor metode de calcul mai generale, bazate pe lucrul mecanic care se efectuaza la o deplasare oarecare a corpurilor, asupra carora cāmpul electric actioneaza printr-o forta electrica medie, numita forta generalizata , notata cu X; deplasarea medie a corpurilor din sistem ca urmare a acestei forte punānd numele de coordonata generalizata, notata cu x.

Pe baza acestor doua notiuni s-au emis teoremele fortelor generalizate, valabile īn cazul corpurilor conductoare situate īn cāmpul electrostatic.

Prima teorema a fortelor generalizate

Se presupune ca dupa īncarcarea conductoarelor, acestea se deconecteaza de la sursele externe, astfel ca sarcinile corpurilor ramān constante.

Energia elementara, primita de la sursele exterioare pentru cresterea sarcinii pe conductoare (), trebuie sa acopere atāt cresterea de energie a conductoarelor, cāt si lucrul mecanic efectuat de cāmp pentru deplasarea corpurilor din sistem. Deoarece la un moment dat si , aceasta energie devine egala cu zero:

Din (3.5.14) rezulta:

sau :

Interpretare fizica: cānd sursele exterioare sunt deconectate, lucrul mecanic se poate produce numai pe seama resurselor interne de energie ale sistemului, respectiv prin scaderea acestei energii.

Enuntul teoremei :

Forta generalizata X, corespunzatoare coordonatei generalizate x, este egala cu derivata cu semn schimbat a energiei īn raport cu coordonata generalizata, la sarcini constante ale conductoarelor.

A doua teorema a fortelor generalizate

Se presupune ca toate corpurile conductoare sunt conectate la bornele unor surse exterioare de tensiune constanta (). Pāna la atingerea valorii corespunzatoare lui , cāmpul electric al corpurilor din sistem creste, facānd ca acestea sa interactioneze si sa modifice configuratia geometrica a sistemului.

Rezulta ca variaza capacitatile dintre conductoare, deci variaza si sarcinile acestora (), pāna la un nou echilibru electrostatic.

Energia elementara primita de la sursele exterioare duce la variatia energiei interne a sistemului si la compensarea lucrului mecanic efectuat pentru deplasarea corpurilor:

La , variatia de energie a sistemului este:

si reprezinta, dupa cum se vede, jumatate din energia elementara primita de la sursele exterioare.

Rezulta ca produsul din rel. (3.5.17) reprezinta cealalta jumatate, adica:

Asadar, ca interpretare fizica, aportul de energie din exterior se īmparte, īn mod egal, īntre cresterea energiei cāmpului si lucrul mecanic efectuat de fortele electrice asupra corpurilor din sistem.

Ca urmare:

Enuntul teoremei:

Forta generalizata X, corespunzatoare coordonatei generalizate x, este egala cu derivata energiei īn raport cu coordonata generalizata, la potentiale constante ale conductoarelor.

Cele doua expresii, ale celor doua teoreme, sunt echivalente, permitānd obtinerea unor rezultate identice.

3.6. Prezentare succinta a metodelor electrostaticii

Prin metodele electrostaticii se īnteleg metodele de determinare a cāmpurilor si potentialelor electrostatice īn diferite medii sau corpuri.

Printre metodele mai importante se pot evidentia:

1. metoda elementara; 2. metoda imaginilor; 3. metoda ecuatiei Laplace; 4. metoda diferentelor finite.

Īn continuare vor fi prezentate unele dintre aceste metode si anume: 1. metoda elementara, 3. metoda ecuatiei Laplace si 4. metoda diferentelor finite.

Metoda elementara

Aceasta metoda consta īn aplicarea legilor si teoremelor specifice regimului electrostatic, sub forma integrala. Este usor aplicabila īn cazul īn care cāmpul electric prezinta proprietati de simetrie, care permit stabilirea directa a formei liniilor de cāmp.

Exemplu

Se va calcula cāmpul electric si potentialul unui fir rectiliniu infinit de forma cilindrica, īncarcat uniform cu densitatea de sarcina (fig. 3.6.1).

Se observa ca īn acest caz cāmpul este radial si identic īn toate punctele pe directia unei raze , aflate la egala distanta de axul conductorului. Se va alege o suprafata de forma unui cilindru care circumscrie o portiune din conductor, coaxial cu aceasta ,si se va aplica teorema lui Gauss acestei suprafete:

Dar:

vectorii si īn acest fiind perpendiculari īntre ei.

Ramāne din integrala doar termenul referitor la suprafata laterala, astfel ca:

si fiind omoparaleli.

Integrānd relatia (3.6.2) se obtine:

Pe de alta parte, conform aceleiasi teoreme se poate scrie:

Prin egalarea celor doua expresii (3.6.3) si (3.6.4) se obtine expresia cāmpului electric sub forma:

Cum , rezulta si, īnlocuind īn (3.6.5), rezulta:

sau, vectorial:

Relatia (3.6.7) exprima intensitatea cāmpului electric īntr-un punct oarecare P, la distanta de axul conductorului, considerānd raza acestuia comparabila cu aceasta distanta ().

Potentialul electric īntr-un punct oarecare P , situat īn exteriorul conductorului, este dat de relatia:

presupunānd punctul chiar si pe suprafata conductorului infinit.

Rezulta:

relatie care se mai poate scrie sub forma:

Metoda ecuatiei Laplace

Pentru a obtine ecuatia lui Laplace īntr-un dielectric omogen (), aflat īn cāmp electric, se va īnlocui expresia (forma locala a teoremei potentialului electrostatic) īn expresia (forma locala a legii fluxului electric), īn conditiile īn care īn dielectric nu exista distributie de sarcina electrica libera ():

Dezvoltānd relatia (3.6.11), se obtecuatia lui Laplace:

ce caracterizeaza īn orice punct P un dielectric lipsit de sarcini si strabatut de liniile de cāmp electrostatic (fig. 3.6.2)

Exemplu

Se va determina expresia potentialului electrostatic īn orice punct din dielectricul unui condensator plan (fig. 3.6.3).

Īn acest scop se poate utiliza metoda ecuatiei Laplace, deoarece īn dielectric si dielectricul este omogen ().

Cum cāmpul electric se dezvolta numai dupa directia Ox, ecuatia Laplace se simplifica īn acest caz, ramānānd:

Integrānd de doua ori suscesiv relatia (3.6.13), se obtine:

constantele si fiind determinate īn urmatoarele conditii:

a.       se alege originea potentialelor pe prima armatura, astfel ca pentru x=0; rezulta V(x)=V(0)=0 si, de aici, ;

b.      se considera pe armatura din stanga sarcina +q si se aplica legea fluxului electric unei suprafete īnchisa care cuprinde aceasta armatura:

Cum , pentru dielectrici liniari, devine:

Se īnlocuieste din expresia :

īn cea a fluxului electric, obtinānd:

Cum si sunt omoparaleli, se mai poate scrie:

Suprafata armaturii condensatorului fiind A, rezulta:

Cum īnsa:

(rel. 3.6.14),si, īnlocuindu-l īn (3.6.19), se obtine:

De unde:

Īnlocuind pe īn expresia potentialului (3.6.14) ,rezulta, īn final:

Pentru x=o, V(0)=0,iar pentru x=d:

Verificarea se poate face prin calculul capacitatii electrice a condensatorului plan, utilizānd expresia potentialului (3.6.22):

Metoda diferentelor finite

O metoda aproximativa, utilizata īn cazul corpurilor cu forme diferite, este metoda diferentelor finite - metoda cu eroare controlabila care foloseste, īn locul ecuatiilor cu derivate partiale ale potentialului, ecuatii cu diferente finite. Se presupune īn acest caz ca potentialul pe frontiera corpului analizat este dat (cunoscut).

Fie un domeniu bidimensional , caracterizat printr-un cāmp laplaceian (fara distributie de sarcina electrica, continānd numai linii de cāmp ). Se pune problema determinarii repartitiei potentialului electric īn acest domeniu (fig. 3.6.4). Pentru aceasta se va īmparti domeniul īn mici patrate de latura h si se vor nota nodurile retelei astfel obtinute cu (unde k = 1...n).

Fiecare punct are coordonatele () si potentialul .

Se dezvolta īn serie Taylor potentialele din jurul fiecarui nod , unde i = 1....4, dupa care se scriu potentialele punctelor īn functie de potentialul :

Se aduna aceste ecuatii si se obtine:

Fiind vorba de un cāmp Laplaceian, potentialul īn fiecare punct al domeniului va satisface ecuatia lui Laplace, care īn acest caz are forma:

Problema care se pune deci este de a gasi solutia acestei ecuatii care ia pe frontiera a domeniului anumite valori (conditiile de frontiera).

Neglijānd īn rel. (3.6.26) termenii īn si tinānd seama de ecuatia (3.6.27), se obtine ecuatia lui Laplace īn diferente finite, bidimensionale, de forma:

care se poate explicita īn raport cu :

Potentialul unui nod al retelei este media aritmetica a potentialelor nodurilor vecine.

Scriind astfel de relatii () pentru toate nodurile si tinānd seama de valorile pe frontiera impuse potentialului (respectiv īn nodurile din vecinatatea frontierei), se obtine un sistem de n ecuatii cu n necunoscute. Pentru rezolvarea sistemului se poate utiliza metoda lui Cramer sau o metoda de iteratie, folosind calculatorul electronic.