Grafuri orientate. Aplicatii

1.Definitii

In cadrul grafurilor orientate ('directed graphs') arcele sunt orientate, avand un sens precizat.

Grafurile orientate ponderate se mai numesc si 'retele' (networks).

2.Problema drumurilor minime cu origine unica

Algoritmul lui Dijkstra

Algoritmul lui Dijkstra pentru determinarea drumurilor minime cu origine unica este in principiu asemanator algoritmului prezentat in lucrarea anterioara, de determinarea a drumurilor minime cu origine unica prin ca utare bazata pe prioritate.

Se considera un graf orientat ponderat, G=(N,A), fiecarui arc a=(i,j) din A ii este asociat un cost COST[i,j].

Algoritmul utilizeaza o structura de date multime M i n care mentine nodurile din N pentru care cea mai scurta distanta pana la nodul origine e deja cunoscuta. Aceasta multime M corespunde mult imii nodurior 'vizitate' deja. M se initializeaza cu nodul de start.

Algoritmul cuprinde mai multe iteratii, in cadrul fiecarei iterat ii se selecteaza un nod x din mult imea N-M, cu proprietatea ca x este cel mai aproape de nodul de start si se trece in mult imea M a nodurilor vizitate. Se verifica apoi pentru fiecare nod y ramas in N-M daca nu exista un drum mai scurt de la nodul origine spre y, drum care trece prin x.

Algoritmul utilizeaza un tablou D, D[i] fiind lungimea celui mai scurt drum de la origine la nodul numarul i la un moment dat. Initial, D[i]=COST[origine,i]. Pe masura ce se gasesc noduri x,y astfel incat D[y]>D[x]+COST[x,y], D[y] este redus. La terminarea algoritmului, D[i] va contine lungimea drumului minim de la origine la i.

procedure Dijkstra;


begin
* initializeaza multimea M a nodurilor vizitate, introduce nod_origine in M
* pentru toate nodurile i, initializeaza lungimea drumului minim pana la i
(D[i]) cu lungimea arcului direct de la nod_origine la i
while ( * mai exista noduri in N-M ) do
begin
* alege un nod x apartina nd multimii N - M astfel i ncat D[x]
sa fie minim si il adauga pe x la M;
for * fiecare nod y din N-M do
* test daca drumul de la nod_origine la y folosind ca punct intermediar nodul x
este mai scurt decit cel memorat anterior, si daca da, actualizeaza D[y]
in forma D[y] := min(D[y],D[x] + COST[x,y]);
end
end;

In vederea reconstructiei traseurilor drumurilor minime de la nodul de start la fiecare nod al gr 949e46j afului, se poate utiliza un alt tablou Parinte de noduri, in care Parinte[x] contine nodul care precede nodul x i n cadrul drumului minim. Initial, Parinte[i]= 1 pentru toate nodurile, cu except ia nodului 1(nodul de start). Elementul Parinte[y] va fi actualizat in momentul actualiza rii lui D[y], daca D[x]+COST[x,y]<D[y] atunci Parinte[y]:=x;

Tabloul Parinte contine un arbore de acoperire minim al grafului G.

Problema determinarii drumurilor minime corespunzatoare unui nod precizat al unui graf se reduce de fapt la determinarea unui arbore de acoperire care are drept radacina nodul in cauza.

Algoritmul lui Dijkstra opereaza asupra grafurilor dense orientate, reprezentate prin matrici de adiacenta. Se executa n iteratii pentru selectarea tutoror nodurilor, iar in cadrul fiecarei iteratii se face o parcurgere a tuturor nodurilor inca neselectate y pentru ajustarea tabloului D. Performant a algoritmului este deci O(n^2).

Daca a este mult mai mic deca t n2, este mai indicat ca i n reprezentarea grafului sa se foloseasca liste de adiacent e, respectiv o coada bazata pe prioritate pentru a pastra nodurile mult imii N-M. In acest caz, algoritmul lui Dijkstra devine algoritmul de determinare a drumurilor minime cu origine unica folosind cautarea bazata pe prioritate, prezentat in lucrarea anterioara.

3.Problema drumurilor minime corespunzatoare tuturor perechilor de noduri. Algoritmul lui Floyd

Se considera un graf orientat G=(N,A), in care fiecare arc a=(i,j) din A are o pondere pozitiva COST[i,j]. Problema drumurilor minime corespunzatoare tuturor perechilor de noduri presupune determinarea, pentru fiecare pereche ordonata (i,j), a lungmii drumului minim care conecteaza i cu j.

O rezolvare a acestei probleme este aplicarea repetata a algoritmului lui Dijkstra avand ca nod origine fiecare nod al grafului.

O alta metoda de rezolvare directa a acestei probleme este data de algoritmul lui Floyd.

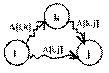
Algoritmul utilizeaza o matrice A de dimensiuni NxN, in care A[i,j] va fi lungimea drumului minim de la i la j. Initial, se presupune ca drumul minim de la i la j este arcul (i,j). Se testeaza apoi fiecare nod k al grafului, pentru a vedea daca pentru fiecare pereche de noduri i,j nu exista un drum mai scurt de la i la j trecand prin k (figura 1), adica daca suma drumurilor minime de la i la k s i de la k la j nu este mai mica decat drumul considerat minim de la i la j.

Pentru a determina traseele drumurilor minime, se poate introduce o matrice Drum de dimeniune NxN, Drum[i,j] memoreaza acel nod k care conduce i n cadrul algoritmului la scurtarea drumului A[i,j]. Se va alege o valoare speciala pentru 'nod inexistent'. Daca Drum[i,j]=nod inexistent, atunci cel mai scurt drum de la i la j este arcul direct.

procedure Floyd;


begin
* init ializeaza matricea lungimilor drumurilor minime A[i,j]) si matricea
nodurilor intermediare de pe trasee (Drum[i,j]) presupunand ca drumul minim
intre oricare doua noduri este arcul direct
for * fiecare nod k al grafului do
for * fiecare pereche de noduri i,j do
if (* suma drumurilor de la i la k s i de la k la j e mai mica decat drumul de la
i la j ( A[i,k] + A[k,j] < A[i,j] )) then
begin
* actualizeaza valoarea drumului minim, prin A[i,j] := A[i,k] + A[k,j]
* memoreaza punctul de pe traseu, Drum[i,j] := k
end
end;

Pentru reconstituirea traseelor, se poate folosi urmatorul algoritm recursiv. Algoritmul afiseaza traseul drumului minim intre intre doua noduri specificate, nodurile i si j.

procedure Traseu(i,j:integer);


begin
if ( *exista cel putin un nod k=Drum[i,j] intermediar de la i la j)
then
begin
Traseu(i,k);
writeln(k);
Traseu(k,j);
end;
end;

Timpul de executie al algoritmului lui Floyd este de ordinul O(n3).

In timp ce versiunea algoritmului lui Dijkstra determina drumurile minime cu origine comuna in O(n2) i n cazul grafurilor dense implementate prin matrici de adiacente, deci aplicarea de n ori a procedurii Dijkstra duce la o performanta O(n3),in cazul grafurilor rare reprezentate prin liste de adiacenta, algoritmul lui Dijkstra este de ordinul O(a log n), deci aflarea tuturor drumurilor minime se poate face cu o performanta O(a n log n).

4.Traversarea grafurilor orientate

Cele doua tehnici fundamentale de traversare a grafurilor (cautartea in adancime si ca utarea prin cuprindere), prezentate intr-o lucrare anterioara au un caracter general s i pot fi aplicate si in cazul grafurilor orientate, tinand cont, in timpul traversarii, de orientarea arcelor examinate.

5.Grafuri orientate aciclice. Sortarea topologica

Aceste grafuri pot fi considerate ca o categorie aparte, situataintre arbori si grafurile orientate. Grafurile orientate aciclice pot fi utilizate pentru a reprezenta relatii de ordonare partiala.

Fie M o multime si M M multimea tuturor perechilor ordonate de elemente din M. O relatie R pe multimea M este o submultime a lui M M.

O relatie R este o relatie de ordine partiala daca este reflexiva, tranzitiva si antisimetrica. Pot exista elemente a,bIM care nu pot fi comparate (nu sunt adevarate nici una din propozitiile (a R b) sau (b R a)

In cadrul unui graf orientat aciclic, se poate defini o relatie de ordine partiala. Fie N multimea nodurilor grafului. Se defineste relatia de ordine partiala £ pe multimea N in felul urma tor: pentru nodurile u,vIN, se spune ca u£ v daca exista un drum i n graf de la u la v.

Sortarea topologicaa elementelor uI N presupune alcatuirea unei secvente contina nd toate elementele din N, astfel i ncat nici care doua elemente consecutive sa nu incalce relat ia de ordine partiala . Oricare doua elemente consecutive din secvent a sunt i n relatia £ sau intre ele nu este definita nici o relatie.

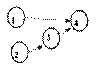
Exemplu: Se considera graful din figura 2. Exista mai multe secvente ce pot reprezenta o ordine de sortare topologica a nodurilor sale.

1 , 2 , 3 , 4

2 , 3 , 1 , 4

2 , 1 , 3 , 4

Sortarea topologica are numeroase aplicat ii practice, in diverse situat ii de planificare a unor activitati.

Un algoritm de sortare topologica, adaptare a algoritmului de cautare in adancime, este prezentat in continuare.

procedure SortTopologic (x:Nod);


begin
* marcheaza nodul x ca vizitat;
for (*fiecare nod k adiacent lui x) do
if (*k este nevizitat)
then
SortTopologic(k);
writeln(x);
end;

Afisarea (prelucrarea, memorarea) nodurilor se face in ordine topologica inversa. Daca aplicatia necesita ordinea topologica directa, se poate face memorarea nodurilor intr-o stiva , urmand a fi apoi extrase din stiva si prelucrate i n ordinea buna. Spre deosebire de algoritmul de cautare in ada ncime, algoritmul de sortare topologica realizeaza afisarea la revenirea din apelul recursiv de cautare i n adancime, si nu la vizitarea nodului.

Algoritmul original de cautare in ada ncime nu produce in general o secventa in ordine topologica , numai in unele cazuri particulare.

De exemplu, pentru graful din figura 2, cautarea i n adancime produce secventa:

1 , 4 ; 2 , 3 ;

Algoritmul de sortare topologica produce secventa:

4 , 1 ; 3 , 2 ;

Inversul ei este

2 , 3 , 1 , 4 ceea ce este o secventa ordonata topologic.

6.Exercitii

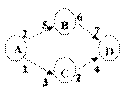
6.1. Se considera graful din figura 3.

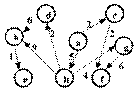
Sa se aplice algoritmul lui Dijkstra pentru determinarea tututor drumurilor minime care pornesc din nodul a.

Se va ilustra ordinea de selectie a nodurilor si pasii i n constructia arborelui de acoperire corespunzator drumurilor minime.

6.2. Se considera graful orientat aciclic din figura 4.

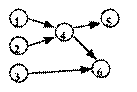
Sa se gaseasca urmatoarele secvent e de noduri:

secvent a rezultata prin aplicarea algoritmului de sortare topologica

secvent a rezultata prin aplicarea algoritmului de traversare in ada ncime

7.Probleme de implementare

7.1.Se cere sa se realizeze urma toarele doua implementari ale algoritmului lui Dijkstra:

pentru grafuri reprezentate prin matrice de adiacente

pentru grafuri reprezentate prin liste de adiacente. In acest caz, se vor folosi ansamble (arbori binari partial ordonat i) pentru implementarea cozilor bazate pe prioritate.

Algoritmul va calcula lungimile si traseele tuturor drumurilor minime cu originea intr-un nod oarecare x.

Se vor compara performantele celor doua implementari, prin ma surarea timpilor de executie in cazul unor grafuri cu un numar mare de noduri.

7.2. Sa se implementeze o functie pentru calculul drumului minim de la un nod oarecare x la un nod oarecare y al unui graf orientat ponderat. Se va analiza performanta functiei si se va compara timpul de executie a acesteia cu timpul de executie al algoritmului lui Dijkstra, pentru determinarea lungimilor tuturor drumurilor minime care pornesc din x.

8.Aplicatii

8.1. Procesul de fabricatie s i asamblare al unui produs cuprinde mai multe faze tehnologice (operatii). Exista anumite faze tehnologice care nu pot fi incepute inainte de i ncheierea altora. Aceste relat ii de precedenta legate de natura procesului de fabricatie sunt cunoscute, ca si timpul de execut ie necesar fiecarei faze. Sa se realizeze un program care primeste ca si date de intrare aceste informatii si calculeaza:

In ce succesiune trebuie sa execute un muncitor toate operatiile, pentru a rezulta un produs bun?

Care este timpul in care se termina executia, i n cazul in care lucrarea este facuta de un singur muncitor?

Care este timpul cel mai scurt in care se poate termina executia, daca lucreaza in paralel o echipa de muncitori?

Indicatii

Procesul tehnologic se poate modela sub forma unui graf ponderat orientat aciclic. Nodurile sunt fazele procesului tehnologic, iar un arc de la x la y are semnificatia ' faza y nu poate incepe inainte de i ncheierea fazei x'.

Timpul de execut ie necesar unei faze este o informat ie intrinseca a nodului corespunzator. De exemplu, figura 5 prezita graful unui proces mult simplificat de constructie a unei case, i mpreuna cu durata (i n luni) a fiecarei faze de constructie.

a,b.)Succesiunea in care un singur muncitor trebuie sa realizeze operatiile este data de o secventa sortatai n ordine topologica a nodurilor grafului.

c.)In cazul in care se lucreaza in echipa , neexistand restrict ii asupra numarului muncitorilor implicat i in proiect, o serie de operatii se pot rezolva in paralel. Timpul in care se termina executia, daca se lucreaza la gradul maxim de paralelism, va fi dat de lungimea celui mai lung drum existent i n graf. Lungimea unui drum este definita aici ca suma ponderilor nodurilor care il compun.

Cel mai lung drum al grafului este unul dintre drumurile care au ca prim nod un nod de intrare (nici un arc nu intrain acest nod), s i ca ultim nod un nod de iesire (nu exista nici un arc cu originea in acest nod).

Se vor testa toate drumurile din aceasta categorie.

Observatie: este posibil ca i ntre un anumit nod de intrare si un anumit nod de iesire sa existe un drum, mai multe drumuri sau nici un drum.

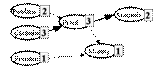
8.2. Transportul de ca la tori intre n localitati ale unui judet este asigurat cu ajutorul unor autobuze. Intre oricare doua localitati I si J exista cel mult un autobuz direct, care merge o data pe zi, avand un orar cunoscut (ora de plecare din I si ora de sosire i n J, numere intregi). Sa se gaseasca timpul total in care un calator poate ajunge dintr-o localitate oarecare X in alta localitate Y. Se considera ca persoana se afla i n statia din localitatea X la ora 0 si trebuie sa ajunga in Y pana la ora 24 a aceleiasi zile.

Indicatii

Se considera urmatoarea situat ie:

Fie A, B, C, D patru localitati i ntre care exista urmatoarele legaturi:

plecare din A la ora 2, sosire in B la ora 5

plecare din A la ora 1, sosire in C la ora 3

plecare din B la ora 6, sosire in D la ora 7

plecare din C la ora 2, sosire in D la ora 4

Localitatea de plecare este A (ora 0) si localitatea de sosire este D. Cel mai devreme, se poate ajunge in D la ora 7.

Aceasta problema este o varianta a problemei drumului minim. Se poate aplica o varianta derivata din algoritmul lui Dijkstra

Fie N=mult imea localitatilor.

Fie M= mult imea localitatilor pentru care se cunoaste deja timpul minim de sosire pe un drum cu originea in localitatea de start.

Pentru fiecare nod I , fie TimpMin[I]= timpul minim la care se poate sosi cel mai devreme in I pornind din localitatea de start.

Algoritmul este urmatorul:

Initializeaza mult imea M cu multimea formata din localitatea de start

Initializeaza TimpMin pentru fiecare nod I cu timpul la care ajunge cursa directa de la localitatea de start la I sau cu INFINIT daca nu exista

Ata ta timp cat nu s-a ajuns i n localitatea de destinat ie si mai exista localitati i n N-M care au TimpMin<INFINIT

alege o localitate x apartina nd multimii N-M pentru care TimpMin este minim si o adauga la M

pentru fiecare nod y din N-M, verifica daca exista o cursa care pleaca din x spre y la un moment dupa sosirea in x s i daca aceasta duce la un timp minim mai bun pentru y

8.3. Intre cursurile oferite spre audiere studentilor unei facultati exista relatii de genul: 'cursul x poate fi urmat numai dupa absolvirea cursurilor a,b,.'. Sa se redacteze un program care, ava nd ca date de intrare datele privitoare la cursuri, stabileste si afiseaza:

pentru o persoana care doreste sa participe la toate cursurile, care este o ordine bunain care le poate urma?

fiind dat un anumit curs, care sunt toate cursurile care trebuie sa fie absolvite inainte de i nceperea lui?

8.4.Grafurile orientate aciclice pot fi utilizate la reprezentarea structurii sintactice a expresiilor aritmetice care contin subexpresii comune. De exemplu, figura 7 prezinta un astfel de graf pentru expresia: (a+b)*c+(a+b)+d

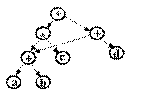
Sa se realizeze un algoritm de evaluare a expresiilor date sub forma unor astfel de grafuri.

Sa se scrie un algoritm de transformare a arborelui binar a unei expresii in graful orientat aciclic care optimizeaza calculul subexpresiilor comune