Proiect MSEI Metode de regresie

UNIVERSITATEA "POLITEHNICA" TIMISOARA

FACULTATEA DE AUTOMATICA SI CALCULATOARE

Proiect MSEI

Metode de regresie

Student :

Anul 2008-2009

Generalitati

Analiza de regresie se ocupa in principal cu descrierea tipului de dependenta dintre variabilele unui sistem.

Metodele de regresie permit obtinerea modelului matematic al procesului sub forma unei ecuatii de regresie (model de r 424g66e egresie), pe baza variatiilor aleatoare ale marimilor de intrare si de iesire, culese in decursul functionarii normale a procesului.

Considerand sistemul prezentat in figura, erorile in determinarea marimii de iesire sunt produse in principal de influenta celor p perturbatii.

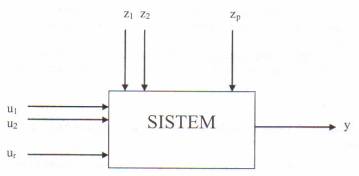
Schema bloc a unui sistem real

Metoda regresiei are ca scop, in primul rand, determinarea pe baza unui numar limitat de masuratori, a dependentei functionale y=f(u₁, .u_r) fara restrictii asupra lui f, si in al doilea rand, stabilirea modului cum se manifesta aceasta dependenta sub actiunea perturbatiilor z_1, ., z_p, care prezinta variatii aleatoare ce nu sunt legate de dependenta functionala studiata, ele nefiind incluse in lista de variabile.

Problema consta in alegerea unei clase de functii in care sa se integreze dependenta functionala (de exemplu, clasa functionalelor liniare sau clasa functiilor de o forma polinomiala data) precum si determinarea coeficientilor ce intervin in expresiile acestor functii - prin minimizarea unei functii criteriu.

Avandu-se in vedere ca in general numarul de ecuatii de care se dispune (de masuratori ale lui y) este mai mare decat numarul de necunoscute (coeficientii modelului de regresie care trebuie determinati) metoda celor mai mici patrate este cea mai utilizata (criteriul fiind cel al erorii medii patratice).

Ca ipoteze de lucru se considera ca parametri procesului sunt constanti, masuratorile sunt de egala precizie sin u exista erori sistematice in cadrul determinarii lui y.

Metoda regresiei aplicata

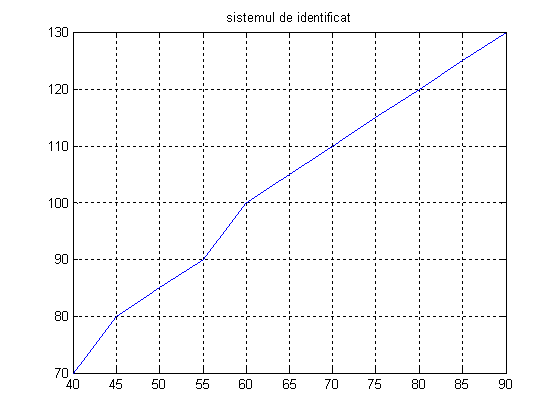
Se studiaza legatura corelationala intre doua marimi u si y ale caror valori masurate sunt date in urmatorul table:

Pentru a alege cea ma buna forma a liniei teoretice de regresie se construieste campul de corelatie pentru fiecare pereche u, y corespunzatoare celor 11 masuratori.

Din modul de amplasare a punctelor in campul de corelatie (u, y) se observa ca dependenta intre u si y poate fi aproximata cel mai bine cu o relatie liniara:

y=a+b*u

Modelul anterior este un model de regresie liniara, iar a si b sunt coeficientii regresiei.

Punctele experimentale se vor abate de la dreapta de aproximare cu o eroare calculabila cu relatia:

ε_i=y_i -y_i

Metoda utilizata pentru calculul regresiei este metoda celor mai mici patrate (CMMP), conform careia se vor studia patratele acestor abateri (erori), iar coeficientii a si b ai liniei teoretice de regresie vor fi determinati din conditia ca suma acestor abateri patratice sa fie minima:

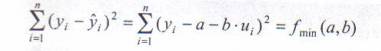
unde n - numarul de puncte din campul de corelatie.

Pentru a detremina acest minim se impune ca derivatele partiale in raport cu coeficientii a si b sa fie nule, obtinandu-se un sistem de 2 ecuatii de forma:

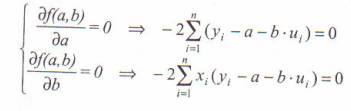
Rezulta ecuatiile normale:

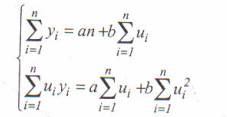
Din sistemul anterior se pot determina usor coeficientii regresiei a si b, folosind una dintre metodele consecrate (metoda substitutiei, metoda Kramer etc.).

Experienta identificatorului are un rol important in alegerea modelului regresiei ai carei coeficienti urmeaza sa fie determinati.

Uzual, ecuatia regresiei se allege sub forma unui polinom de un anumit grad fixat (gradul I, II, III etc.), determinarea coeficientilor facandu-se ca si in cazul regresiei liniare.

Regresia de ordinul 1:

u=40:5:90;

y=[70 80 85 90 100 105 110 115 120 125 130];

plot(u,y), grid, title('sistemul de identificat')

%se calculeaza sumele care apar in sistemul de ecuatii

sy=0;

su=0;

suy=0;

su2=0;

//su3=0;

//suy1=0;

N=length(u);

for i=1:N

sy=sy+y(i);

su=su+u(i);

suy=suy+u(i)*y(i);

su2=su2+u(i)*u(i);

end

%se calculeaza coeficientii regresiei

a=(su*suy-su2*sy)/(su*su-su2*N);

b=(suy*N-su*sy)/(su2*N-su*su);

%se calculeaza rezultatul regresiei

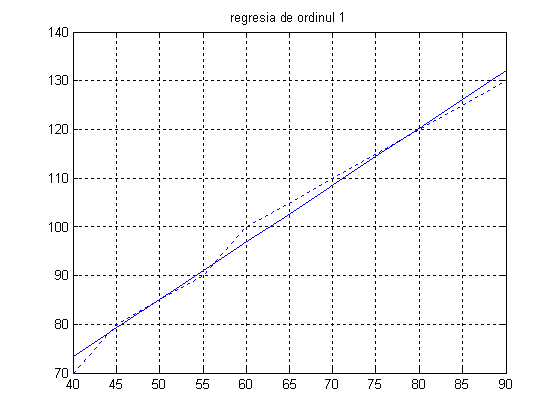
ym=a+b*u

figure

plot(u, ym), grid, title('regresia de ordinul 1')

hold on

plot(u, y, ':')

Regresia de ordinul 2:

u=40:5:90;

y=[70 80 85 90 100 105 110 115 120 125 130];

plot(u,y), grid, title('sistemul de identificat')

%se calculeaza sumele care apar in sistemul de ecuatii

sy=0;

su=0;

suy=0;

su2=0;

su3=0;

suy1=0;

N=length(u);

for i=1:N

sy=sy+y(i);

su=su+u(i);

suy=suy+u(i)*y(i);

su2=su2+u(i)*u(i);

suy1=suy1+u(i)*y(i);

su3=su3+u(i)*u(i);

end

%se calculeaza coeficientii regresiei

c=(su*suy-su2*sy)/(su2*N);

b=(suy*N-su*sy)/(su2*N-su*su);

a=(suy1*N-su*sy)/(su3*N-su*su);

%se calculeaza rezultatul regresiei

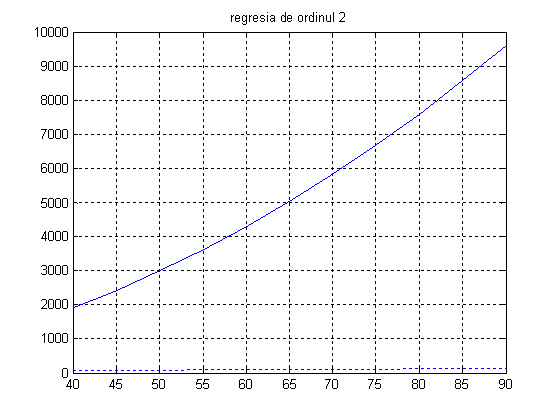
ym=a.*u.*u+b.*u+c;

figure

plot(u,ym), grid, title('regresia de ordinul 2')

hold on

plot(u,y,':')

Regresia de ordinul 3:

u=40:5:90;

y=[70 80 85 90 100 105 110 115 120 125 130];

plot(u,y), grid, title('sistemul de identificat')

%se calculeaza sumele care apar in sistemul de ecuatii

sy=0;

su=0;

suy=0;

su2=0;

su3=0;

su4=0;

suy1=0;

suy2=0;

N=length(u);

for i=1:N

sy=sy+y(i);

su=su+u(i);

suy=suy+u(i)*y(i);

su2=su2+u(i)*u(i);

suy1=suy1+u(i)*y(i);

suy2=suy2+u(i)*y(i);

su3=su3+u(i)*u(i);

su4=su4+u(i)*u(i);

end

%se calculeaza coeficientii regresiei

d=(su*suy-su2*sy)/(su2*N);

c=(suy*N-su*sy)/(su2*N-su*su);

b=(suy1*N-su*sy)/(su3*N-su*su);

a=(suy2*N-su*sy)/(su4*N-su*su);

%se calculeaza rezultatul regresiei

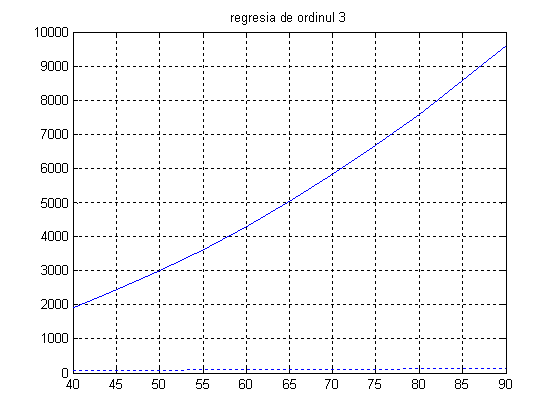
ym=a.*u.*u+b.*u+c;

figure

plot(u,ym), grid, title('regresia de ordinul 3')

hold on

plot(u,y,':')