ARII
TRIUNGHIURI SI PATRULATERE
CLASA a VII-a
1.Triunghiul oarecare
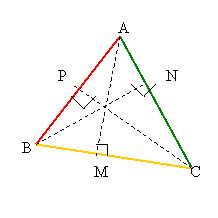
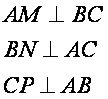
sunt inaltimile
triunghiului 
. Se noteaza de obicei cu 
.
Laturile triunghiului se numesc baze. Avem mai multe formule pentru calculul ariei triunghiului :
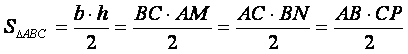
sau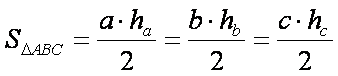 
Aceasta este formula de baza pentru calculul ariei unui triunghi.
Vom studia tot in clasa a 7-a si urmatoarele formule:
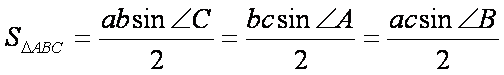
2. Triunghiul dreptunghic.
La triunghiul dreptunghic avem doua formule pentru calculul ariei:
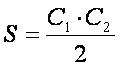formula
de baza, ca la triunghiul oarecare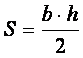 
pe care daca notam
ipotenuza cu I , o putem scrie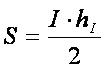 
. Deoarece celelalte doua inaltimi ale triunghiului
dreptunghic sunt chiar catetele , vom putea scrie
(daca notam catetele
cu 
)
Observatii.
Daca avem un
punct 
vom putea scrie aria triunghiului ABC ca o suma de doua arii:
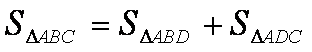
Aceasta este proprietatea de aditivitate pentru arii si este importanta in aplicatii practice, cand vrem sa calculam aria unei figuri geometrice pentru care nu avem o formula specifica pentru calculul ariei.
2. Doua triunghiuri care au ariile egale se numesc echivalente.
3. Mediana unui triunghi imparte triunghiul in doua triunghiuri echivalente.
3.Aria unui patrulater convex.
Aria unui patrulater convex este egala cu suma ariilor triunghiurilor in care acesta se descompune.
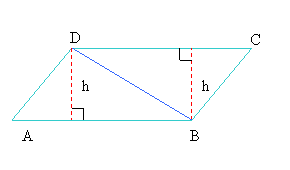i)Aria paralelogramului
Inaltimea paralelogramului este distanta dintre o latura si latura opusa ei, h.
Paralelogramul ABCD se poate descompune in doua triunghiuri ABD si BCD.
Avem in acest caz: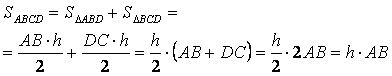 
deoarece AB=CD
Deci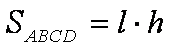 
O alta formula pentru aria paralelogramului:
Daca notam cele doua laturi cu l si L, mai putem scrie aria paralelogramului si astfel:
ii) Aria dreptunghiului.
iii) Aria patratului
iv) Aria rombului.
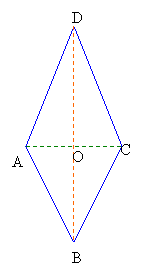Rombul fiind un paralelogram
putem folosi formula de la aria paralelogramului. 
Daca descompunem rombul in doua triunghiuri
vom obtine o noua formula :
=
=
=
=
=
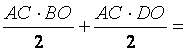
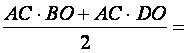
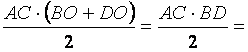
Deci aria rombului mai poate fi si semiprodusul diagonalelor.
Aria trapezului
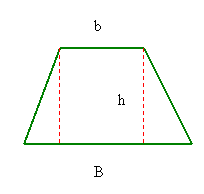Daca notam bazele trapezului cu B si b, iar
inaltimea
cu h avem: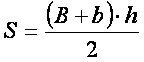
Stiind ca linia mijlocie a trapezului este
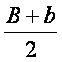putem
sa scriem ca
|
