Analiza combinatorie

Analizã combinatorie

XII.1. Permutãri

Definitia XII.1.1. O multime împreunã cu o ordine bine determinatã de dispunere a elementelor sale este o multime ordonatã si se notazã (a₁,a₂,.,a_n).

Definitia XII.1.2. Se numesc permutãri ale unei multimi A cu n elemente toate multimile ordonate care se pot forma cu cele n elemente ale lui n. Numãrul permutãrilora n elemente, n N*, este P_n=1 2 3 . n = n!; 0! = 1 (prin definitie).

Factoriale (proprietãti): n! = (n - 1)!n; n! =

XII.2. Aranjamente

Definitia XII.2.1. Se numesc aranjamente a n elemente luate câte m (m n) ale unei multimi A cu n elemente, toate submultimile ordonate cu câte m elemente care se pot forma din cele n elemente ale multimii A. Se noteazã A^m_n.

Numãrul aranjamentelor a n elemente luate câte m este:

A^m_n = n(n - 1).(n - m + 1) = 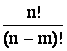, n m.

Proprietãti: Aⁿ_n = P_n; Aⁿ_n = sau Aⁿ_n= n!; .

XII.3. Combinãri

Definitia XII.3.1. Se numesc combinãri a n elemente luate câte m (m n) ale unei multimi A cu n elemente toate submultimile cu câte m elemente, care se pot forma din cele n elemente ale multimii A. Se noteazã .

Proprietãti:

;

;

Numãrul submultimilor unei multimi cu n elemente este 2ⁿ;

;

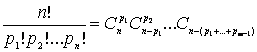unde p₁ + . p_m-1 < n

XII.4. Binomul lui Newton

(x + a)ⁿ =

(x - a)ⁿ = unde n N

Proprietãti:

Termenul de rank k+1 este T_k+1 = (-1)^kx^n-ka^k;

;

T_k+2 = T_k+1 sau T_k+2 = T_k+1;

Numãrul termenilor dezvoltãrii (x a)ⁿ este n+1;

Coeficientii termenilor egal depãrtati de extremi sunt egali.

Relatii importante:

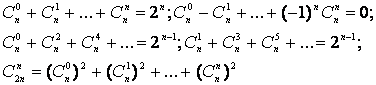
Dezvoltãri particulare uzuale:

(a b)² = a² 2ab + b²;

(a + b + c)² = a² + b² + c² + 2(ab + bc + ac);

(a + b)³ = a³ + 3a²b + 3ab² + b³;

(a - b)³ = a³ - 3a²b + 3ab² - b³;

(a + b + c)³ = a³ + b³ + c³ + 3(a²b + a²c + b²a + b²c + c²a + c²b) + 6abc;

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

XII.5. Suma puterilor asemenea ale primelor n numere naturale

Dacã S_p = 1^p + 2^p + .+ n^p, p N, atunci avem:

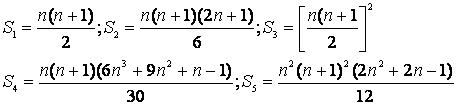
O relatie care permite calculul lui S_p, când se cunosc S_p-1, S_p-2,., S₁ este formula lui Pascal: (n+a)^p+1 = 1+