Aceasta lucrare face referire la functiile MATLAB:

det calculeaza determinantul unei matrice;

inv calculeaza inversa matricei;

rank calculeaza rangul matricei;

trace calculeaza urma unei matrice;

cond estimeaza numarul de conditionare al matricei;

condest estimeaza numarul de conditionare al matricei;

norm calculeaza norma vectorului sau matricei;

rcond estimeaza numarul de conditionare al matricei.

1.Determinantul unei matrice

Calculul determinantului unei matrice se face cu functia det, se apeleaza cu sintaxa: D=det(X)

Exemplul.1.1.Calculati determinantii urmatoarelor matrice:

A= B= .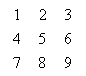

Cu secventa MATLAB:

A=[1 2; 3 4]; B=[1 2 3; 4 5 6; 7 8 9];

A1=det(A)

B1=det(B)

se obtine rezultatele:

A1= -2 B1= 0

2.Inversa unei matrice

Inversa unei matrice se calculeaza cu functia inv, se apeleaza cu sintaxa:

Y=inv(X)

Exemplul 2.1. Calculati inversa matricei:A=.

Cu secventa MATLAB:

A=[2 1; -1 1];

B=inv(A)

se obtine rezultatul:  B=

0.6667

3.Rangul unei matrice

Rangul unei matrice reprezinta numarul de linii sau coloane liniar independente ale acesteia si se determine cu functia rank; se apeleaza cu una dintre sintaxele:

r=rank(X) r=rank(X,tol)

Exemplul 3.1. Sa se determine rangul matricei A= .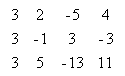

Cu secventa MATLAB:

A=[3 2 -5 4;3 -1 3 -3;3 5 -13 11];

k=rank(A)

care returneaza: 

k= 2

4.Urma unei matrice

Urma matricei - suma elementelor de pe diagonala principala - se calculeaza cu functia trace; se apeleaza cu sintaxa:

u=trace (A)

Exemplul 4.1. Sa se calculeze urma matricei A=.

Cu secventa MATLAB:

A=[1 2 3;4 5 6; 7 8 0];

B=trace(A)

se obtine rezultatul:

B= 6

5.Calculul normelor vectorilor si matricelor

Norma este un scalar care da o masura a "marimii " elementelor unei matrici sau vector. Normele vectorilor si matricelor se calculeaza cu functia norm; se apeleaza cu una dintre sintaxele:

n=norm (X) n=norm(X,p) n=norm(X,'fro')

6.Conditionarea unei matrice

Numarul de conditionare al unei matrice, calculat ca raportul dintre cea mai mare si cea mai mica valoare singulara a acesteia, se determina cu functia cond; se apeleaza cu sintaxa: c=cond(X)

O functie mai performanta care permite calculul numarului de conditionare este rcond, se apeleaza cu sintaxa:

c=rcond(X)

Estimarea celui mai mic de conditionare se face cu functia condest, se apeleaza cu sintaxa:

c=condest(X)

Exemplul 6.1. Calculati numerele de conditionare pentru sistemul de ecuatii:

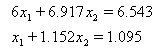
si de asemenea pentru sistemul "perturbat"

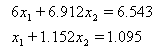
cu secventa MATLAB:

A1=[6 6.917;1 1.152];

A2=[6 6.912;1 1.152];

c1=cond(A1);c2=cond(A2);

d1=condest(A1);d2=condest(A2);

r1=rcond(A1);r2=rcond(A2);

se obtin rezultatele:

c1=1.7234e+004 c2=Inf

d1=2.0845e+004 d2= 2.7129e+017

r1=5.4453e-005 r2=4.1842e-018

de unde rezulta ca sistemul este rau-conditionat. Acest lucru se verifica si prin rezolvarea celor doua sisteme, cu valori "apropiate" ale coeficientilor (diferenta la a patra cifra).

Cu secventa MATLAB:

A1=[6 6.917; 1 1.152];

A2=[6 6.912;1 1.152];

b=[6.543;1.095]

x1=A1 b

x2=A2 b

se obtin rezultatele:

x1=[7.3158 -5.4000]

x2=[-8.1041 7.0348]*1.0e+013

Slaba conditionare a matricei sistemului se reflecta īn diferentele foarte mari ale solutiilor.