CALCUL DE ARII SI VOLUM

CALCUL DE ARII SI VOLUM - CALCULEAZA ONLINE

CLASA a 8-a

ARIA SI VOLUMUL CUBULUI

Daca cubul are muchia egala cu l avem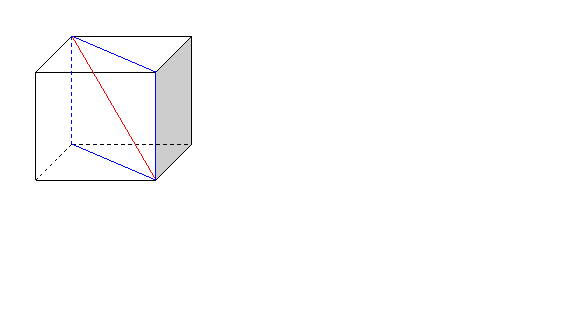

ARIA=6l - calculeaza online

VOLUM=l - calculeaza online

PROBLEMA1.

PROBLEMA2

Fie un cub cu latura de 3cm.

Unind centrul cubului cu varfurile se obtin 6 piramide congruente. Ce volum are fiecare dintre aceste piramide?

PROBLEMA 3

Figura albastra se numeste sectiune diagonala a cubului si este formata de doua diagonale a fetelor si o diagonala a cubului.

Ea separa cubul in doua prisme triunghiulare. Ce volum au aceste prisme ?

PROBLEMA 4( problema din manualul de cl. A 8-a prof. Singer, prof. Voica)

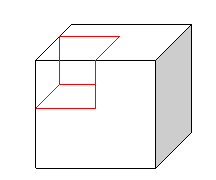Din unul din colturile unui cub de lemn cu latura de 4cm se indeparteaza o bucata cubica cu latura de 2cm. Calculeaza volumul si aria corpului asfel obtinut.

PROBLEMA5.

Calculeaza si compara de cate ori se mareste aria si volumul unui cub daca latura se dubleaza.

PROBLEMA 6.

Diagonala unui cub este 12 959b16j cm.Calculeaza in mmaria cubului , apoi aproximeaza in dmvolumul cubului. Cat este diagonala cubului?

2.ARIA SI VOLUMUL PARALELIPIPEDULUI DREPTUNGHIC.

Dimensiunile

Lungimea L

Latimea l

Inaltimea h

Diagonala D

ARIA =2(Ll +Lh +lh)

VOLUM=Lhl sau A∙h

Sectiunea diagonala (una din ele ) este formata ca si in cazul cubului de diagonalele a doua fete opuse si diagonala paralelipipedului.

PROBLEMA 1.

PROBLEMA 2

Una din fetele unui paralelipiped este un patrat cu latura de 3cm, iar unghiul dintre doua diagonale este de 60.Calculeaza volumul.

PROBLEMA 3

Dimensiunile unui paralelipiped sunt proportionale cu 3, 4, 5 iar aria este 376cm.Calculeaza volumul.

PROBLEMA 4

Un corp in forma de paralelipiped cu dimensiunile de 4cm, 3cm, 2cm este taiat in doua cu un plan ce trece prin doua din diagonalele bazelor. Calculeaza volumele corpurilor astfel obtinute.

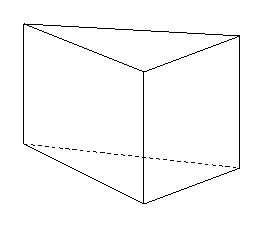ARIA LATERALA, ARIA TOTALA SI VOLUMUL PRISMEI

Cubul si paralelipipedul dreptunghic sunt prisme in care orice fata poate fi considerata ca baza. Nu orice prisma are aceasta proprietate. Ca exemplu avem prisma triunghiulara din figura. Aria laterala este suma ariilor felelor sale laterale. Aria totala este formata din aria laterala si ariile celor doua baze.

ARIA LATERALA

ARIA TOTALA

VOLUMUL 

PROBLEMA 1

PRISMA HEXAGONALA

PROBLEMA 2

Prisma hexagonala ABCDEFAare muchia bazei 3cm iar(AD;BD)=60 Calculeaza :

--inaltimea prismei

--verifica daca BD┴(ABC)

--determina aria laterala , aria totala, volumu

ARIA LATERALA ,TOTALA , SI VOLUMUL

PIRAMIDEI

ARIA LATERALA

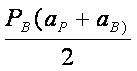
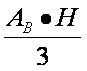ARIA TOTALA =ARIA LAT.+ARIA BAZEI =

VOLUMUL

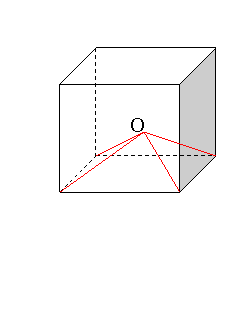Fie cubul din figura cu centrul in O.( intersectia diagonalelor).

Unind punctul O cu varfurile cubului se obtin 6 piramide, avand ca baze fetele cubului.Deoarece volumul cubului este aputem spune ca volumul unei piramide este .

Putem calcula volumul unei piramide si cu formula data anterior.

APLICATIE

Putem calcula distanta de la un punct la un plan calculand in doua moduri volumul unei pir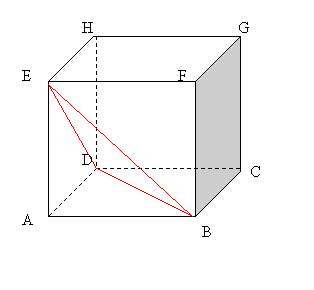amide.

Sa calculam distanta de la punctul A la planul (BDE) Luam tetraedrul ABDE cu baza ADE , apoi ca baza BDE .

V=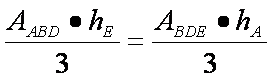 deoarece h=EA si triunghiul BDE este echilateral obtinem d(A,(BDE))=h=

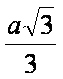
unde a este muchia cubului.

ARIA LATERALA, ARIA TOTALA SI VOLUMUL TRUNCHIULUI DE PIRAMIDA

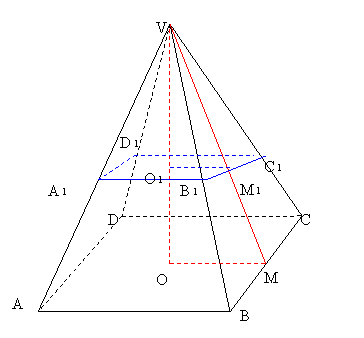
Notam OM-

OM-

VO-H

ΔVOM~ΔVOM

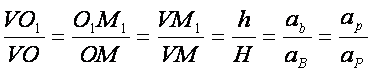
Pentru a calcula aria laterala a trunchiului putem facem diferenta dintre aria laterala a piramidei mici si aria laterala a piramidei mari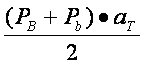: A = (a) Pentru a calcula volumul vom proceda la fel ,facand diferenta dintre volumul piramidei mari si volumul piramidei mici.

Vom obtine formula  V=)

PROBLEMA 1 Sa se completeze tabelul de mai jos pentru trunchiul de piramida patrulatera regulata

Raportul a doua segmente omoloage se numeste raport de asemanare si se noteaza de obicei cu k.

Raportul ariilor bazelor, raportul ariilor fetelor laterale a doua piramide asemenea = k

Raportul volumelor a doua piramide asemenea =k

PROBLEMA 2

Intr-o piramida hexagonala regulata cu latura bazei de 4cm si 9cm, se fac doua sectiuni paralele cu baza ce impart inaltimea in trei segmente congruente.Calculati ariile sectiunilor si lungimilor laturilor lor, apoi volumele corpurilor obtinute.

Demonstrati ca aria laterala a corpului din mijloc este media aritmetica a ariilor laterale ale celorlalte doua corpuri.

PROBLEMA 3

Se da o piramida patrulatera regulata cu inaltimea 8cm. La ce distanta fata de baza trebuie dus un plan paralel cu baza astfel incat raportul dintre volumul trunchiului obtinut sivolumul  piramidei initiale sa fie 7/8.

PROBLEMA 4

Sa se demonstreze formula pentru volumul trunchiului de piramida patrulatera regulata.

Un trunchi de piramida patrulatera regulata are latura bazei mari L, latura bazei mici l si inaltimea h. Sa se calculeze in functie de L,l, h , inaltimea piramidei din care provine trunchiul.

Rezolvare

Stim ca V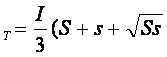

Am notat I inaltimea trunchiului si cu S si s ariile bazelor. Putem demonstra aceasta formula stiind ca :

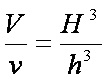rezulta ; dar V-v= ;rezulta V= 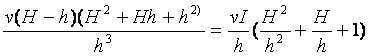Dar rezulta ca

V=