Corelatii

Corelatii

Introducere

Organismul uman este de departe cel mai complex sistem cunoscut de noi în univers. În functionarea unui sistem sunt importante cunoasterea parametrilor de functionare ai acestuia. De-a lungul timpului, oamenii de stiinta au studiat sistemele considerând ca acestea sunt caracterizate de un numar mai mic sau mai mare de asa-numiti parametri interni ai sistemului care caracterizeaza starea acestuia.

În functie de starea sistemului la un moment dat, el poate reactiona într-un fel sau altul la asa-numitele variabile de intrare, facând sistemul sa treaca într-o alta stare si, eventual sa produca anumite variabile de iesire. Daca ar fi sa facem o paralela, atunci pentru organismul uman variabilele de intrare sunt conditiile de mediu, atât cele care se refera la conditiile în care organismul traieste si îsi desfasoara activitatea cât si actiuni mai mult sau mai putin momentane asupra lui cum ar fi actiunile permanente si vitale ca satisfacerea nevoilor de sete, foame, relatiile cu semenii, etc. Parametrii interni ar fi, daca am continua aceasta paralela, toate acele marimi care caracterizeaza starea organismului atât momentan cât si ca evolutie în timp. Variabilele de iesire ar fi actiunile fiintei umane ca raspuns la conditiile de mediu.

Aceasta paralela ar putea fi continuata printr-un studiu mai amanuntit al interrelatiilor care se nasc în mod natural între toate variabilele de intrare si de iesire, conditionate mai mult sau mai putin de parametrii interni. Din pacate acest mod de abordare a organismului uman pune probleme atât de complexe încât rezultatele concrete care eventual s-ar putea obtine dintr-o astfel de abordare s-ar lasa foarte mult asteptate.Organismul uman este atât de complex încât nu se poate pune problema de a îl cuprinde în ecuatii si formule oricât de complexe, cuprinzatoare si numeroase ar fi ele.

De aceea, suntem obligati la a aborda un eventual studiu din perspectiva teoriei sistemelor al organismului uman sa procedam simplificator si sa încercam:

Fie studiul prin formule a relatiilor mai simple care se nasc în interiorul organismului uman atunci când separam în masura posibilului subsisteme mai simple, cum ar fi sistemul reglarii setei, al foamei, reflexe simple etc. De fapt si aceste sisteme, oricât de simple ni s-ar parea la prima vedere nu pot fi modelate decât prin simplificari si aproximari care sa nu altereze prea mult esentialul si sa fie rezonabile din punctul de vedere al eventualului efort de calcul.

Fie separarea unui numar restrâns de parametri interni între care se cauta corelatiile mai mult sau mai putin asteptate. Vom cauta bineînteles sa stabilim daca odata cu variatia unuia sau mai multor parametri regasim o variatie corespunzatoare a altor parametri, care în felul acesta pot fi cumva studiati având în vedere aceste corelatii pe care eventual le-am gasi.

9.2 Notiunea de corelatie

Functionarea organismul ca un tot unitar este conditionata de conlucrarea într-o armonie perfecta a unei miriade de factori, multi dintre ei înca necunoscuti. Legaturile dintre ei sunt de o complexitate ce ne scapa deocamdata pe alocuri. Cunoasterea umana, cu toate progresele facute, a reusit sa de 21421w2211v zvaluie ceea ce am putea numi valul exterior al proceselor complexe din organism. Ramân de studiat corelatii pe care acum nici nu le banuim sau pe care le cunoastem doar superficial si trebuie sa le aprofundam.

Pentru a explica notiunea de corelatie, vom exemplifica câteva legaturi între parametri de macrosistem, adica parametri ce caracterizeaza organismul în totalitatea lui sau sistemele mai importante din organism. Astfel, stim cu totii ca exista o corelatie între tensiunea arteriala sistolica si cea diastolica. Ce înseamna acest fapt? Înseamna ca tendinta de crestere a tensiunii sistolice, este însotita de o tendinta de crestere si a tensiunii diastolice, iar tendinta de scadere a primeia este însotita de o tendinta de scadere a celei de-a doua.

Tot astfel, alte perechi de parametri manifesta o comportare asemanatoare: greutatea si înaltimea, numarul de eritrocite si hemoglobina, vitezele de sedimentare a hematiilor la o ora si la doua ore, colesterolemia si lipemia, etc. Trebuie subliniat ca variatia concomitenta a celor doi parametri se manifesta numai ca tendinta, nu este o regula. Pot exista indivizi cu tensiunea sistolica foarte mare si cea diastolica normala sau invers, indivizi cu tensiunea sistolica normala si cea diastolica scazuta. Totusi, majoritatea indivizilor manifesta tendinta de a avea valori crescute sau scazute, pentru ambele concomitent.

Definitie:

Vom spune ca doi parametri care au tendinta de a creste sau descreste simultan sunt direct corelati.

Asa cum a fost data mai sus, notiunea de corelatie se refera la tendinta de crestere sau descrestere simultana a doi parametri indiferent cît de puternica sau de slaba este aceasta tendinta. Vom vedea mai departe ca este nevoie de o cuantificare a tariei corelatiei între doi parametri, altfel discutiile nu pot fi nuantate si corelatia ar fi o notiune prea putin utila.

Pe de alta parte, exista cazuri în care doi parametri se coreleaza prin cresterea unuia însotita de o tendinta de descrestere a celuilalt. Astfel, cresterea concentratiei hormonului tiroidian T₄, este însotita de o scadere a frecventei cardiace. Acesti doi parametri sunt un exemplu de corelatie inversa.

Definitie:

Vom spune ca doi parametri sunt corelati invers daca au tendinta ca, odata cu cresterea sau descresterea unuia, celalalt sa descreasca sau sa creasca. (au tendinta inversa de variatie).

Trebuie facute câteva observatii care sa clarifice cele introduse mai sus si sa evite o folosire abuziva a termenului de corelatie:

Corelatiile le vom cauta pentru parametri care pot fi masurati cantitativ si deci sunt exprimati prin numere.

Nu vom cauta corelatii, cel putin nu în sensul definitiei de mai sus între parametri calitativi care se exprima prin simboluri nenumerice, adica care produc date nominale sau ordinale.

Tendinta de corelatie o putem întelege în mai multe sensuri dintre care doua intereseaza mai mult domeniul medicinii:

Tendinta unui parametru de a se schimba de la pacient la pacient poate fi însosita de tendinta altui parametru de a se schimba în acelasi sens sau invers

Corelatii în sensul ca un parametru variaza la acelasi individ, de exemplu în timp, si variatia este însotita de o variatie corepunzatoare a altui parametru, la acelasi pacient

Exemple de situatii în care avem corelatie între doi parametri sunt redate în figurile 9.1, 9.2 si 9.3. În figura 9.1, sunt reprezentate valorile bilirubinei totale si ale bilirubinei directe la 235 de pacienti cu ciroze hepatice si cancer hepatic. Se observa o corelatie extrem de puternica, din forma norului de puncte care este extrem de alungit si subtire.

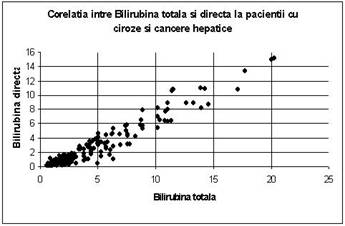
Figura 9.1 Valorile bilirubinei totale si ale bilirubinei directe la 235 de pacienti cu ciroze hepatice si cancer hepatic. Se observa o corelatie extrem de puternica, din forma norului de puncte care este extrem de alungit si subtire

În figura 9.2, sunt reprezentate valorile pentru hormonul tiroidian T4 si cele ale hormonului T3, la 9 pacienti cu hipertiroidie si 9 pacienti hipotiroidie. Valorile sunt puternic corelate, fapt care se observa din forma norului dublu de puncte care se aliniaza de-a lungul unei linii aproape drepte. Faptul ca norul este întrerupt nu are o relevanta prea mare în acest caz. La mijlocul norului de puncte lipsesc de fapt valorile normale. Pacientii pentru care s-au facut masuratorile, având diferite forme de tiroidii, valorile pentru cei doi hormoni sunt extreme.

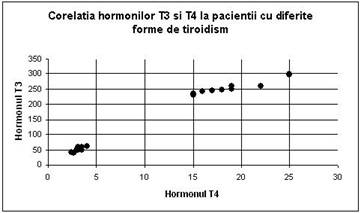
Figura 9.2 Valorile pentru hormonul tiroidian T4 si cele ale hormonului T3, la 9 pacienti cu hipertiroidie si 9 pacienti hipotiroidie. Valorile sunt puternic corelate, fapt care se observa din forma norului dublu de puncte care se aliniaza de-a lungul unei linii aproape drepte.

În figura 9.3 este dat un alt exemplu de pereche de parametri care se coreleaza puternic: VSH la o ora si VSH la doua ore. Norul foarte alungit si subtire, arata tendinta de corelatie. Cele câteva puncte care sunt mult în afar norului, tradeaza erori de introducere adatelor. Acest exemplu ne spune si ca unele din valorile aberante pot fi oservate pe graficul de corelatie.

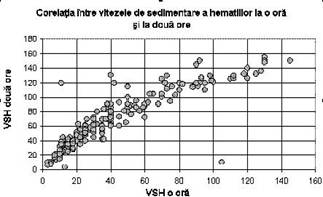
Figura 9.3 VSH la o ora si VSH la doua ore. Norul foarte alungit si subtire, arata tendinta de corelatie

În figura 9.4 se observa ca între valorile sodiului seric si potasiului seric ale pacientilor cu afectiuni hepato-renale nu exista nici o corelatie, deoarece datele sunt distribuite aproximativ întâmplator. Nu se poate observa o tendinta clara ca punctele graficului sa fie asezate într-un fel anume, în afara de tendinta naturala ca densitatea sa fie mai mare în mijloc, tendinta care se poate observa în general, la majoritatea datelor în medicina si biologie si nu numai. Pe de alta parte, tendinta punctelor de a se aseza într-un singur nor, arata omogenitatea seriei de valori.

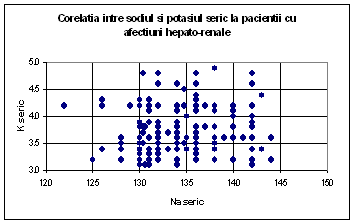
Figura 9.4 Valorile sodiului seric si potasiului seric la 235 de pacienti cu afectiuni hepato-renale. Nu exista corelatie, deoarece punctele norului sunt distribuite întâmplator.

În ce priveste graficul punctual (SCATTER), se va urmari totdeauna trei tipuri diferite de informatie pe care acesta ni le poate oferi:

• daca cele doua serii de valori sunt corelate (Corelatia).
• daca esantionul pe care s-au facut masuratorile este omogen sau este eterogen (Omogenitatea).
• anumite informatii despre simetria distributiei celor doua serii de valori (Simetria).

Exemple:

În graficul din figura 9.4 se observa ca între valorile sodiului seric si potasiului seric ale pacientilor cu afectiuni hepato-renale nu exista nici o corelatie, deoarece datele sunt distribuite aproximativ întâmplator. Nu se poate observa o tendinta clara ca punctele graficului sa fie asezate într-un fel anume, în afara de tendinta naturala ca densitatea sa fie mai mare în mijloc, tendinta care se poate observa în general, la majoritatea datelor în medicina si biologie si nu numai. Pe de alta parte, tendinta punctelor de a se aseza într-un singur nor, arata omogenitatea seriei de valori.

În graficul din figura 9.1, se observa ca între valorile bilirubinei totale si bilirubinei directe ale pacientilor cu ciroze si cancere hepatice exista o corelatie puternica, deoarece datele sunt distribuite aproximativ de-a lungul unei linii drepte. De asemeni, esantionul este omogen, ca si în cazul graficului 1, lucru care se observa din faptul ca norul de puncte nu are tendinta de a se divide în doi nori diferiti.

Pe de alta parte se vede ca norul este mult mai dens în stânga jos. Deci, valorile din seria bilirubinei totale (orizontala), sunt distribuite asimetric (valori mai multe în stânga = asimetrie dreapta). La fel, valorile din seria bilirubinei directe (verticala), sunt mai dense jos, la valori mici, deci sunt distribuite tot asimetric (asimetrie dreapta).

În figura 9.2, se observa ca între valorile hormonilor tiroidieni T4 si T3 ale pacientilor cu diferite forme de tiroidism exista o corelatie datele fiind distribuite tot de-a lungul unei linii, chiar daca este discontinua. De asemeni, se observa ca distributia lor este grupata: o grupa cu valori mici pentru cei doi hormoni indicând hipotiroidienii si o grupa cu valori mari pentru cei doi hormoni indicând hipertiroidienii, adica o tendinta clara de separare în doi nori diferiti. Spunem în acest caz ca esantionul este eterogen sau neomogen.

La fiecare grafic de acest tip este bine sa fie urmarite cele trei tipuri de informatie pe care poate sa ni le ofere (Corelatie, Omogenitate si Simetrie). Unele ne dau o informatie mai utila privind corelatia, altele ne informeaza mai bine în ce priveste omogenitatea sau simetria, deci nu totdeauna se pot obtine dintr-un singur grafic toate cele trei tipuri de informatie la fel de usor. Aprecierile sunt totdeauna subiective si depind de deprinderile pe care utilizatorul si le-a format lucrând cu cât mai muote si mai variate exemple.

9.3 Coeficientul de corelatie PEARSON

Este clar ca o exprimare a tendintei de corelatie astfel încât sa surprindem taria corelatiei este foarte utila. De-a lungul timpului au fost propuse mai multe metode de masurare a tendintei de corelatie, dintre ele cele mai utile s-au dovedit acelea care propun coeficienti ce tin cont de toate valorile pe care le avem la dispozitie.

Coeficientul de corelatie PEARSON este de departe cel mai utilizat în exprimarea tariei corelatiei între doi parametri numerici.

Anume, fie si , valorile masurate pentru cei doi parametri si fie , mediile de esantionare respective. Atunci coeficientul de corelatiile al parametrilor exprimati de seriile statistice X si Y va fi:

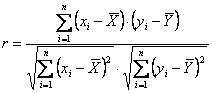
Aceasta formula, care la prima vedere pare foarte complicata, ne ofera în realitate într-un mod relativ simplu, o valoare numerica care, se va vedea mai jos, apreciaza foarte obiectiv situatia de fapt în ceea ce priveste corelatia.

Pentru a întelege cum functioneaza formula de mai sus sa luam un exemplu: tensiunile arteriale sistolica si diastolica masurate la 10 pacienti sunt urmatoarele:

Tensiunea sistolica TMAX: 170, 160, 160, 150, 150, 170, 160, 180, 150, 150.

Tensiunea diastolica TMIN: 85, 80, 80, 75, 80,, 85, 80, 85, 75, 75

Se observa ca pentru calculul lui r avem nevoie de mediile celor doua serii statistice, si , si pentru fiecare pacient în parte de diferentele si , care pentru numarator trebuie înmultite între ele, iar pentru numitor trebuie ridicate la patrat si apoi sumate pentru toti pacientii. Deoarece valorile au fost alese special ca sa se usureze calculele, se observa ca mediile pentru TAMAX si TAMIN sunt =160 si =80. Este bine ca toate calculele necesare pentru gasirea lui r sa fie organizate într-un tabel asa cum se vede în tabelul 9.1:

Tabelul 9.1 Calculul coeficientului de corelatie Pearson

Calculul lui r este:

Trecând peste faptul ca de obicei calculele sunt putin mai dificile din cauza unor zecimale care apar inerent la calculul mediilor si deci al diferentelor, sa cautam sa vedem ce se poate întâmpla în diverse situatii ce pot apare în legatura cu valorile luate de cei doi parametri. În primul rân sa observam ca la numarator, în cazul nostru, numarul 350 a fost obtinut prin adunarea unor numere pozitive si anume 5x50+100. Dar observam ca valoarea 50 obtinuta pentru al patrulea pacient (ca si la al noualea si al zecelea, de altfel) s-au înmultit doua numere negative, pe când la celelalte valori diferite de 0, la pacientii 1, 6 si 8, numerele au fost obtinute prin înmultirea unor numere pozitive. Acest lucru nu este nici pe de parte lipsit de importanta, ci din contra, este ceea ce caracterizeaza situatia prezentata în mod fundamental.

Sa facem urmatoarele observatii referitoare la cazul prezentat:

Pacientii 4,9 si 10 au si valori TAMAX si TAMIN sub media celor 10 pacienti. Deci diferentele si sunt ambele negative iar produsul lor, cel care se aduna la numarator este pozitiv

Pacientii 1,6 si 8 au si valori TAMAX si TAMIN peste media celor 10 pacienti. Deci diferentele si sunt ambele pozitive iar produsul lor, cel care se aduna la numarator este pozitiv

Pacientii 2, 3, 5 si 7 au valori TAMAX sau TAMIN egale cu media celor 10 pacienti. Deci, dintre diferentele si cel putin una este 0 iar produsul lor, cel care se aduna la numarator este 0.

Ceea ce am precizat în rândurile de mai sus este caracteristic pentru situatiile în care cei doi parametri se coreleaza: cei doi parametri iau valori preponderent în acelasi sens, adica ori ambii sub medie, ori ambii peste medie.

Din cauza tendintei a doi parametri care se coreleaza direct, ca atunci când unul este crescut, sa fie si celalalt crescut, vom fi pentru majoritatea pacientilor în situatii ca mai sus si produsele care se aduna la numarator sunt preponderent pozitive. În acest caz, suma de la numarator tinde sa aiba valori pozitive crescute. Evident, corelatia dintre parametri este doar o tendinta si este probabil sa întâlnim pacienti care, desi au unul din parametri crescut, de exemplu peste medie, celalalt poate sa nu fie crescut, chiar sa fie sub medie, caz în care produsul corespunzator lui va fi negativ. Dar acest fenomen nu este o tendinta daca parametrii sunt corelati ci mai curând accident. Suma obtinuta la numarator va avea tendinta de a lua valori mari si pozitive în ciuda unor astfel de accidente.

Daca cei doi parametri sunt corelati invers, adica tendinta unuia de a avea valori crescute este însotita de tendinta celuilalt de a avea valori scazute, în acest caz, predominante vor fi situatiile în care în produsul , ia des valori negative. Într-adevar, daca un parametru are valori sub medie si celalalt peste medie, o paranteza va fi pozitiva si una negativa. Daca acest fapt este o tendinta, parantezele de la numarator vor fi cele mai multe negative. Suma obtinuta la numarator va avea tendinta de a lua valori mari si negative.

Daca cei doi parametri nu sunt corelati, parantezele de la numarator vor avea semne aleatorii, vor fi unele produse pozitive si unele negative. Tendinta va fi ca cele negative si cele pozitive sa se anuleze unele pe altele. Suma obtinuta la numarator va avea tendinta de a lua valori mici, pozitive sau negative.

Nu am discutat nimic despre numitorul coeficientului r, deoarece el are totdeauna semnul +, iar rolul lui este numai de a face ca r sa fie cuprins între -1 si +1. Magnitudinea lui r, precum si semnul sau, sunt dictate de suma de la numarator. Asadar, orice valori ar lua cei doi parametri, prin calculul lui r, obtinem un numar real cuprins în intervalul de numere reale [-1, 1].

Interpretarea coeficientului de corelatie Pearson se face în termeni extrem de subiectivi si imprecis astfel:

Valori foarte apropiate de 1 arata o foarte puternica corelatie directa

Valori în jurul a 0,7 - 0,9 arata o corelatie puternica

Valori între 0,4 - 0,7 arata corelatie

Valori între 0,15 - 0,4 arata corelatie slaba

Valori sub 0,15 arata lipsa de corelatie

La fel, pentru valori negative pentru anticorelatie (corelatie inversa).

O interpretare obiectiva a lui r este tinând cont de semnificatia lui statistica, care este prezentata în subcapitolul urmator.

9.4 Testarea semnificatiei statistice a lui r

Ca orice variabila aleatoare, r este supus variatiilor datorate întâmplarii si valorile calculate folosind datele pe care le avem la îndemâna sunt aproximative, în sensul ca sunt supuse acestor erori aleatoare. De aceea este foarte util sa se cunoasca distributia unei variabile aleatoare strâns legata de r, pentru construirea intervalelor de încredere. În figura 9.5 este reprezentata curba care descrie valorile coeficientului de corelatie Pearson pentru un numar din ce în ce mai mare de valori în cele doua serii S-a calculat r, pentru latenta masurata pe ochiul stâng si, respectiv drept, la 4 pacienti, apoi la 5 pacienti, apoi la 6 pacienti, si asa mai departe pâna la o valoare a lui r calculata pe datele de la 913 pacienti. Se observa ca pâna la 100-200 de pacienti, valoarea coeficientului r este foarte fluctuanta, dupa care se stabilizeaza relativ.

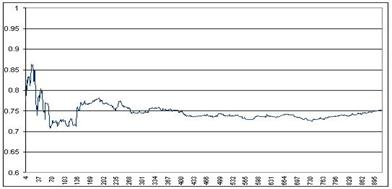
Figura 9.5 Valorile coeficientului de corelatie Pearson calculat pe un numar variabil de valori în cele doua serii. S-a calculat r, pentru latenta masurata pe ochiul stâng si, respectiv drept, la 4 pacienti, apoi la 5 pacienti, apoi la 6 pacienti, si asa mai departe pâna la o valoare a lui r calculata pe datele de la 913 pacienti. Se observa ca pâna la 100-200 de pacienti, valoarea coeficientului r este foarte fluctuanta, dupa care se stabilizeaza relativ.

În cazul esantioanelor mari, se pot folosi nivelurile prag date de , pentru nivelul de semnificatie de 95%, daca n≥50 si respectiv , pentru nivelul de semnificatie de 99%, daca n≥100. Cu ajutorul lor se construiesc intervale de încredere, care sunt o estimare a valorii adevarate a coeficientului de corelatie al populatiei din care afost extras lotul pe care s-au facut masuratorile.

Un test pentru ipoteza r=0 este statistica , care are o distributie Student cu n-2 grade de libertate si poate fi comparata cu valorile prag dorite, luate din tabelele pentru aceasta distributie.

9.5 Notiunea de dreapta de regresie

Daca doi parametri sunt suficient de puternic corelati, atunci cunoscând valoarea unuia dintre ei, celalalt nu ia valori absolut aleatorii ci valoarea pe care acesta o poate lua este într-o legatura mai puternica sau mai slaba cu valoarea primului, în functie de cât de puternic este coeficientul de corelatie între cei doi parametri.

Sa privim putin mai atent pe un grafic (vezi figura 9.6), ce se întâmpla în cazul unei corelatii puternice. Anume, sa reprezentam pe orizontala valorile latentei undei P100 pentru ochiul drept (LD), iar pe verticala valorile latentei undei P100 pentru ochiul stâng (LS), la 913 de pacienti, masurate în milisecunde.

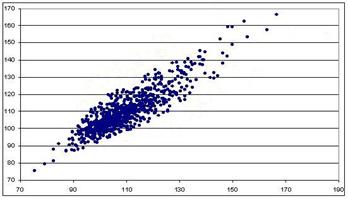
Figura 9.6 Corelatia valorilor latentei undei P100 pentru ochiul drept (verticala) si valorile latentei undei P100 pentru ochiul stâng (orizontala), la 913 de pacienti, masurate în milisecunde. Fiecare punct de pe grafic corespunde unui pacient. Se observa o corelatie puternica din aranjarea norului de puncte, care are o forma alungita.

Asa cum era de asteptat valorile LD si LS se coreleaza, în sensul ca au tendinta de a se aseza într-un nor alungit dinspre stânga jos spre dreapta sus pe grafic, cu unele exceptii, reprezentate de punctele care sunt iesite din nor. De fapt, se observa ca majoritatea punctelor din grafic se aranjaza într-o zona ovala.

În cazurile ca cel din figura 9.6, se poate încerca gasirea unei drepte care sa treaca cât mai aproape de punctele graficului, dreapta care sa reprezinte o legatura între cei doi parametri. În figura 9.7 este reprezentata o astfel de dreapta pentru graficul din figura 9.6. Aceasta dreapta exista pentru nori de puncte foarte diversi, si se numeste dreapta de regresie.

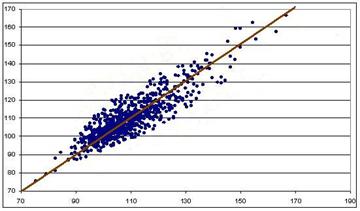
Figura 9.7 Dreapta de regresie pentru cazul latentei semnalului nervos pe cei doi ochi, la apcienti cu diverse afectiuni. Pe orizontala, valorile pentru ochiul stâng, iar pe verticala cele pentru ochiul drept.

Numim aceasta dreapta legatura între cei doi parametri în sensul urmator: daca se cunoaste valoarea de pe orizontala, se poate calcula cu oarecare aproximare valoarea de pe verticala, si invers. În exemplul din figura 9.7, daca stim latenta pentru ochiul stâng, putem calcula cu o anumita aproximatie latenta pentru ochiul drept, si invers. Acest fapt este sugerat în figura 9.8, de sagetile care indica valoarea aproximativa de pe o axa, corespunzatoare unei anumite valori de pe cealalta axa.

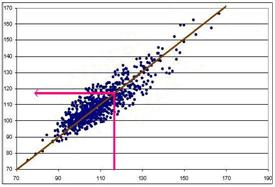
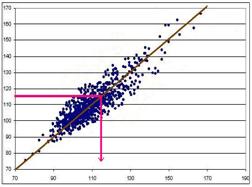
Figura 9.8 Folosirea dreptei de regresie ca legatura între cei doi parametri care sunt puternic corelati

Dreapta de regresie este de obicei cautata prin asa-numita metoda a celor mai mici patrate, expusa în subcapitolul urmator.

9.6 Metoda celor mai mici patrate (MCMMP)

Vom cauta o dreapta care sa se apropie cât mai mult de punctele graficului, dreapta care o vom numi drepta de regresie liniara. Pentru a ne da seama cum intrepretam expresia "se apropie cât mai mult de punctele graficului", sa luam un exemplu simplu, ca cel din figura 9.9.

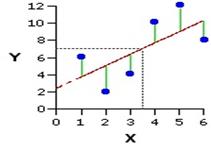
Figura 9.9 O dreapa de regresie se cauta ac dreapta care este situata cât mai aproape de punctele graficului. Distantele de la punctele graficului la dreapta se masoara pe verticala. În imagine, distentele care trebuie sa fie cât mai mici sunt segmente verticale

Vom spune ca o dreapta este dreapta de regresie daca suma distantelor de la puncte la dreapta, masurate pe verticala si ridicate la patrat, este minima.

Dreapta pe care o cautam are ecuatia , si vom întelege prin aceasta ca, odata cunoscuta valoarea parametrului de pe abscisa, x, putem calcula valoarea parametrului de pe ordonata, y, prin înmultirea cu a si adunarea lui b. Asadar, gasirea dreptei de regresie este echivelenta cu gasirea coeficientilor a si b. În figura 9.10 este prezentata o situatie în care dreapta de regresie poate fi folositî pentru aproximarea unui efect Y (care poate fi un rezultat al unei medicatii) în functie de o cauza X (care poate fi medicasia). Se observa ca putem gasi nivelul efectului dupa valoarea luata de factorul cauza. Pentru valoarea 10 a lui X, efectul Y are valoarea aproximativa 1010. Pentru valoarea 50 a lui X, Y ia valoarea 925.

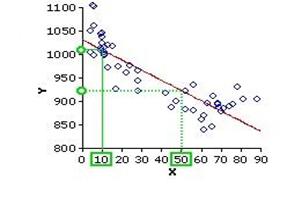
Figura 9.10 Dreapta de regresie ca legatura între cauza si efect. Se observa ca putem gasi nivelul efectului dupa valoarea luata de factorul cauza. Pentru valoarea 10 a lui X, efectul Y are valoarea aproximativa 1010. Pentru valoarea 50 a lui X, Y ia valoarea 925

Proprietatea de baza a dreptei de regresie, se scrie astfel:

ceea ce exprima faptul ca segmentele ce unesc fiecare punct cu punctele de pe dreapta situate pe aceeasi verticala, trebuie sa fie cât mai scurte posibil. Exprimarea aceasta nu este tocmai corecta, ci mai degraba intuitiva, caci, a spune ca segmentele sunt cât mai scurte, nu precizeaza nimic când se refera la toate segmentele. Nu vom sti exact care dintre ele trebuie sa fie mai scurt si care mai lung când suma patratelor lor este minima.

Vom interpreta expresia de mai sus ca o expresie ce contine doua necunoscute, si anume a si b, si dorim aflarea lor pentru a putea fi utilizate în ecuatia , atunci când avem nevoie.

Minimul expresiei ce are ca variabile pe a si pe b, se poate afla printr-un procedeu care este cunoscut din analiza matematica, si anume, minimul unei functii se realizeaza pentru acele valori ale necunoscutei care anuleaza derivata întâi a functiei în raport cu variabila respectiva. În cazul în care avem o functie cu doua variabile, ca cea de mai sus, va trebui sa anulam derivatele ei în raport cu fiecare dintre cele doua necunoscute. Vom scrie deci expresia S astfel ca derivarea în raport cu a si cu b sa fie cât mai facila.

Pentru aceasta, vom folosi formula

,

precum si faptul ca o suma poate fi distribuita, adica este valabila formula:

Astfel vom avea:

si dupa distribuirea de care vorbeam mai sus:

sau, dupa ce scoatem în fata sumelor ceea ce nu depinde de i:

Acum sa nu uitam ca si sunt valorile masurate ale celor doi parametri, care dau pozitiile punctelor de pe grafic, si deci, fiind cunoscute, sumele din expresia lui S sunt cunoscute. De fapt, se obisnuieste ca aceste sume sa fie notate cu urmatoarele notatii, mult folosite în analiza de regresie:

, , , ,

Asadar, sunt numere cunoscute în momentul calculului de care ne ocupam ceea ce face ca expresia lui S sa devina:

Acum pentru a afla minimul lui S vom deriva odata în raport cu a si vom egala cu 0 ceea ce am obtinut, apoi vom deriva în raport cu b si vom egala cu 0 ceea ce am obtinut. Nu trebuie uitat ca, la derivarea în raport cu a, vom considera ca b este constanta si invers. Vom obtine deci relatiile:

si

,

care se vede ca pot fi rescrise ca un sistem de doua ecuatii cu doua necunoscute, în felul urmator:

,

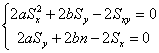sau, dupa trecerea termenilor care nu depind de necunoscutele a si b în partea dreapta si împartirea cu 2 a ambelor egalitati, obtinem:

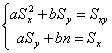
Acesta este, dupa cum se poate usor observa, un sistem de doua ecuatii cu doua necunoscute, chiar în forma cea mai simpla (sistem liniar).

Metoda expusa mai sus se numeste Metoda Celor Mai Mici Patrate (MCMMP), si este mult folosita pentru simplitatea cu care ne pune la dispozitie un rezultat util. Utilitatea acestei metode este mai clar pusa în evidenta atunci când o folosim pentru evaluarea unui efect cuantificabil când cauzele care îl produc pot fi cuantificate suficient de bine. Un bun exemplu este aplicarea unui tratament cu un medicament în diferite doze, daca efectul acestuia este suficient de obiectiv cuantificabil.

Alt exemplu de aplicare utila a metodei celor mai mici patrate este estimarea evolutiei în timp a unor fenomene de intensitate cuantificabila. De exemplu, atunci când am înregistrat numarul anual de cazuri de cancer de sân într-o arie geografica data, si ne punem problema daca este îndreptatita ipoteza unei tendinte de crestere a incidentei acestei maladii. În acest caz, dreapta de regresie este un estimator al vitezei de crestere a incidentei si se poate testa daca exista o crestere semnificativa, iar în caz afirmativ se poate estima cantitativ aceasta tendinta.

9.7 Regresii neliniare

Exista cazuri când dependenta între un efect si o cauza, sau în general între doi parametri nu este liniara. De exemplu, efectul poate sa sufere un fenomen de quasi saturatie si la un moment dat, desi doza creste semnificativ, efectul are o crestere aproape insesizabila, sau invers, la cresteri limitate ale dozei, efectul tinde sa creasca foarte mult. În realitate se pot întâlni extrem de multe astfel de situatii. În aceste cazuri, se cauta nu drepte de regresie ci alte curbe, dupa caz, logaritmice, exponentiale, polinomiale, etc.

Cea mai simpla generalizare este cazul polinomului de gradul al doilea:

caz în care, în mod evident trebuie gasiti trei coeficienti în loc de doi. Cantitatea de minimizat este

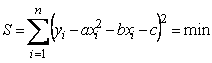
În acest caz, cei trei coeficienti sunt solutiile unui sistem de trei ecuatii cu trei necunoscute, obtinute din egalarea cu 0 a celor trei derivate partiale ale lui S în raport cu a, b si respectiv c:

Au fost folosite si regresii cu polinoame de ordin mai mare, însa pentru a presupune ca între doi parametri este o legatura foarte complexa trebuie puternice dovezi teoretice, care de obicei nu ne stau la dispozitie.

9.8 Regresia liniara multipla

Exista situatii în care este util sa consideram dependenta unui parametru de doua sau chiar mai multi parametri independenti. si în acest caz, Metoda Celor Mai Mici Patrate este de un pretios ajutor. În acest caz, se cauta o dependenta de forma:

unde Y este parametrul care depinde de ceilalti, X₁, X₂,.............X_n sunt parametrii independenti, iar m este numarul lor, uzual având valoarea 2 sau 3, mai rar ajungând la 6 sau 8, foarte rar mai mare.

În acest caz, se pune problema gasirii coeficientilor a₁, a₂,......a_n, astfel ca diferentele dintre valorile masurate Y₁,Y₂,........Y_n, sa fie cât mai apropiate de valorile calculate cu expresia, , unde coeficientii a₁, a₂,......a_n, îi consideram necunoscute si ne propunem sa îi aflam, iar indicele i ne indica masuratoarea, adica:

La masuratoarea 1 se obtin valorile , iar pentru Y valoarea Y₁

La masuratoarea 2 se obtin valorile , iar pentru Y valoarea Y₂

La masuratoarea n se obtin valorile , iar pentru Y valoarea Y_n

De exemplu, pentru dependenta între un parametru dependent si doi independenti, cantitatea de minimizat este:
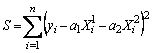