ALTE DOCUMENTE
|
||||||||||
FORME LINIARE, FORME BILINIARE sI FORME PĂTRATICE
Parcurgând aceasta lectie ve ti dobândi cunostinte referitoare la:
Definitia formei liniare, a spatiilor dual si bidual ale unui spatiu vectorial;
Forme biliniare, matricea asociata unei forme biliniare într-o baza data si transformarea sa la schimbarea bazei;
Forme biliniare simetrice si forme patratice;
Metode de aducere a unei forme patratice la o suma de patrate (Gauss, Jacobi), forme patratice pozitiv definite.
Timpul minim pe care trebuie sa-l acordati acestei lectii este de 4 ore.
L.VI.1.1 Spatiul dual
Forme liniare
Se
numeste forma liniara
a spatiului V peste corpul K o functie ![]() având urmatoarele
proprietati:
având urmatoarele
proprietati:
![]()
![]() .
.
Considerând
pe corpul K structura de spatiu
vectorial a lui ![]() pentru
pentru ![]() , se vede ca o forma liniara este o
aplicatie liniara de la V
la K. De aceea se numeste
forma liniara.
, se vede ca o forma liniara este o
aplicatie liniara de la V
la K. De aceea se numeste
forma liniara.
Exemple
1. Fie ![]() o baza a
spatiului V si
o baza a
spatiului V si ![]() o matrice linie având n scalari. Pentru orice vector x al spatiului V sa notam
o matrice linie având n scalari. Pentru orice vector x al spatiului V sa notam ![]() matricea coloana
alcatuita din coordonatele
matricea coloana
alcatuita din coordonatele ![]() ale vectorului x. Din proprietatile
operatiilor cu matrice rezulta ca functia:
ale vectorului x. Din proprietatile
operatiilor cu matrice rezulta ca functia:![]() este o forma liniara a spatiului V.
este o forma liniara a spatiului V.
Deci orice matrice
linie A determina o forma
liniara pe V. În particular,
notând ![]() matricea linie având n elemente, obtinem forma
liniara
matricea linie având n elemente, obtinem forma
liniara ![]() definita
prin:
definita
prin:![]() . Asadar, functia care asociaza fiecarui
vector x prima sa coordonata în
baza fixata
. Asadar, functia care asociaza fiecarui
vector x prima sa coordonata în
baza fixata ![]() este o forma
liniara. Analog se definesc celelalte forme liniare
este o forma
liniara. Analog se definesc celelalte forme liniare ![]() corespunzatoare
celorlalte coordonate ale vectorului variabil x.
corespunzatoare
celorlalte coordonate ale vectorului variabil x.
2. Fie ![]() si sa
notam A o matrice linie având m scalari si B o
matrice coloana având n scalari. Tot din
proprietatile operatiilor cu matrice rezulta ca
asociind fiecarei matrice X de
tip
si sa
notam A o matrice linie având m scalari si B o
matrice coloana având n scalari. Tot din
proprietatile operatiilor cu matrice rezulta ca
asociind fiecarei matrice X de
tip ![]() scalarul
scalarul ![]() obtinem o
forma liniara pe spatiul V.
obtinem o
forma liniara pe spatiul V.
În particular, luând
în loc de A matricea linie cu m elemente toate nule în afara de
cel de pe locul i care este egal cu
unu si în loc de B matricea
coloana având n elemente toate
nule în afara de cel de pe locul j
care este egal cu unu, obtinem faptul evident ca asociind
fiecarei matrice X de tip ![]() elementul sau de
pe linia i si coloana j obtinem o forma
liniara.
elementul sau de
pe linia i si coloana j obtinem o forma
liniara.
3. Fie ![]() si pentru orice
vector
si pentru orice
vector ![]() asociem numarul
real
asociem numarul
real 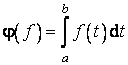 . Din proprietatile de calcul ale integralelor
definite rezulta ca functia φ este o forma
liniara.
. Din proprietatile de calcul ale integralelor
definite rezulta ca functia φ este o forma
liniara.
4. Fie ![]() multimea tuturor
functiilor reale definite pe intervalul
multimea tuturor
functiilor reale definite pe intervalul ![]() si
si ![]() un numar cuprins
între a si b. Din definitia operatiilor cu functii reale,
si anume adunarea functiilor si înmultirea acestora cu
numere reale, rezulta ca functia:
un numar cuprins
între a si b. Din definitia operatiilor cu functii reale,
si anume adunarea functiilor si înmultirea acestora cu
numere reale, rezulta ca functia: ![]() este o forma
liniara pe V.
este o forma
liniara pe V.
Dualul unui spatiu vectorial
În capitolul anterior
am aratat ca pentru orice doua spatii vectoriale V si V peste corpul K, multimea ![]() a aplicatiilor
liniare definite pe V cu valori în
a aplicatiilor
liniare definite pe V cu valori în ![]() are o structura
evidenta de spatiu vectorial peste corpul K.
are o structura
evidenta de spatiu vectorial peste corpul K.
Daca
spatiile V si ![]() sunt finit generate
si se fixeaza o baza în V
având n vectori si alta în
sunt finit generate
si se fixeaza o baza în V
având n vectori si alta în ![]() având m vectori, atunci asociind fiecarei
aplicatii liniare matricea sa în raport cu aceste baze, se obtine un
izomorfism al spatiului
având m vectori, atunci asociind fiecarei
aplicatii liniare matricea sa în raport cu aceste baze, se obtine un
izomorfism al spatiului ![]() pe spatiul
pe spatiul ![]() al matricelor de tip
al matricelor de tip ![]() .
.
Luând în locul lui V' spatiul K, (adica spatiul ![]() pentru
pentru ![]() ) obtinem spatiul vectorial
) obtinem spatiul vectorial ![]() numit dualul spatiului V. Deci dualul spatiului V este alcatuit din formele liniare
ale lui V.
numit dualul spatiului V. Deci dualul spatiului V este alcatuit din formele liniare
ale lui V.
Din cele
mentionate anterior rezulta ca daca V este finit generat, atunci fixând o baza ![]() în V se obtine un izomorfism al
spatiului dual
în V se obtine un izomorfism al
spatiului dual ![]() pe spatiul
pe spatiul ![]() al matricelor linie
având n elemente. Acest spatiu
are aceeasi dimensiune ca si V,
deci este izomorf cu V. Am
obtinut astfel urmatoarea.
al matricelor linie
având n elemente. Acest spatiu
are aceeasi dimensiune ca si V,
deci este izomorf cu V. Am
obtinut astfel urmatoarea.
Propozitie
Daca
spatiul V este finit dimensional
atunci dualul sau, ![]() , este izomorf cu V.
, este izomorf cu V.
De
altfel, acest izomorfism este explicitat în exemplul (1) prezentat mai înainte,
unde se asociaza fiecarui vector ![]() al bazei lui V forma
al bazei lui V forma ![]() , care este tocmai coordonata de indice i.
, care este tocmai coordonata de indice i.
În fond, matricele
linie ![]() ale spatiului
ale spatiului ![]() formeaza tocmai
baza canonica a acestui spatiu izomorf cu
formeaza tocmai
baza canonica a acestui spatiu izomorf cu ![]() . Izomorfismul dintre
. Izomorfismul dintre ![]() este tocmai cel care
asociaza vectorului forma
este tocmai cel care
asociaza vectorului forma ![]() matricea linie
matricea linie ![]() .
.
Baza
![]() a spatiului
a spatiului ![]() asociata bazei
asociata bazei ![]() a lui V se numeste duala bazei
a lui V se numeste duala bazei ![]() . Vectorii (forme)
. Vectorii (forme) ![]() ai bazei duale sunt
definiti de relatiile:
ai bazei duale sunt
definiti de relatiile: ![]() , adica simbolul lui Kronecker, elementul generic al
matricei unitate de ordinul n.
, adica simbolul lui Kronecker, elementul generic al
matricei unitate de ordinul n.
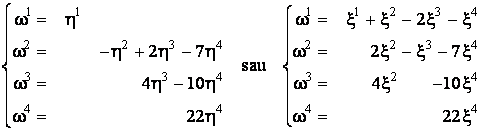
Formula de transformare a bazei duale
Fie
![]() o noua baza
în V, notam
o noua baza
în V, notam ![]() noile coordonate ale
vectorului variabil x din V si
noile coordonate ale
vectorului variabil x din V si ![]() matricea de
trecere de la baza
matricea de
trecere de la baza ![]() la noua baza.
Vectorii bazei duale bazei
la noua baza.
Vectorii bazei duale bazei ![]() îi notam,
fireste,
îi notam,
fireste, ![]() . Ei satisfac conditia:
. Ei satisfac conditia: ![]() . Pe de alta parte, notând
. Pe de alta parte, notând ![]() elementul generic al
matricei
elementul generic al
matricei ![]() , obtinem:
, obtinem:
![]() ,
,
![]() .
.
Asadar, daca T este matricea de
trecere de la baza ![]() la baza
la baza ![]() , atunci matricea de trecere de la baza
, atunci matricea de trecere de la baza ![]() la baza
la baza ![]() este
este ![]() .
.
Totusi
trebuie sa observam ca desi matricea de trecere de la baza
duala celei vechi la baza duala celei noi este aceeasi ca
matricea de trecere de la baza noua la baza veche, adica ![]() totusi formulele
nu sunt identice. Deosebirea se poate releva daca scriem forma
matriceala a acestor formule:
totusi formulele
nu sunt identice. Deosebirea se poate releva daca scriem forma
matriceala a acestor formule:
![]() ;
;
 .
.
Bazele
din ![]() se schimba exact
la fel cum se schimba coordonatele din V,
ceea ce este normal, pentru ca formele bazei duale sunt tocmai
coordonatele.
se schimba exact
la fel cum se schimba coordonatele din V,
ceea ce este normal, pentru ca formele bazei duale sunt tocmai
coordonatele.
Bidualul unui spatiu vectorial
Dualul
dualului unui spatiu vectorial V
se numeste bidualul lui V si
se noteaza ![]() . Elementele sale sunt forme liniare definite pe spatiul
. Elementele sale sunt forme liniare definite pe spatiul
![]() al formelor lui V.
al formelor lui V.
Daca
V este finit generat atunci, asa
cum ![]() are aceeasi
dimensiune cu V, si este deci
izomorf cu V, tot asa dualul
are aceeasi
dimensiune cu V, si este deci
izomorf cu V, tot asa dualul ![]() al lui
al lui ![]() este izomorf cu
este izomorf cu ![]() . Asadar bidualul
. Asadar bidualul ![]() al lui V este izomorf cu V.
al lui V este izomorf cu V.
Un
izomorfism al lui V pe ![]() se obtine
compunând izomorfismul h al lui V pe
se obtine
compunând izomorfismul h al lui V pe ![]() definit de baza
duala, cu izomorfismul analog, k, al lui
definit de baza
duala, cu izomorfismul analog, k, al lui ![]() pe
pe ![]() .
.
Interesant este faptul ca în timp ce izomorfismele h si k depind de baza aleasa în V si, în general, se modifica odata cu schimbarea acestei baze (daca se schimba baza lui V, atunci izomorfismele h si k nu vor mai fi aceleasi), compunerea lor, k h, este un izomorfism intrinsec, adica nu depinde de baza aleasa în V.
Propozitie
Izomorfismul
k h
al lui V pe ![]() se defineste
prin:
se defineste
prin: ![]() .
.
Demonstratie
Sa
consideram o baza ![]() a lui V , sa notam
a lui V , sa notam ![]() baza duala din
baza duala din ![]() si
si ![]() baza lui
baza lui ![]() duala bazei
duala bazei ![]() .
.
Izomorfismul h este definit prin: ![]() adica
matricea lui h în raport cu cele
doua baze, baza aleasa în V
si duala sa din
adica
matricea lui h în raport cu cele
doua baze, baza aleasa în V
si duala sa din ![]() , este matricea
unitate. În consecinta, daca vectorul x din V are coordonatele
, este matricea
unitate. În consecinta, daca vectorul x din V are coordonatele ![]() , atunci vectorul
, atunci vectorul ![]() va avea aceleasi
coordonate în baza
va avea aceleasi
coordonate în baza ![]() a lui
a lui ![]() si la fel si
vectorul
si la fel si
vectorul ![]() în baza
în baza ![]() a lui
a lui ![]() , adica:
, adica:
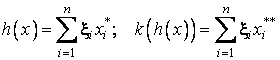
Pe de alta parte, forma ![]() a spatiului V , se defineste prin:
a spatiului V , se defineste prin: ![]() si, analog, forma
si, analog, forma
![]() a lui
a lui ![]() se defineste
prin:
se defineste
prin: ![]() . Ca urmare, fixând vectorul x si notând
. Ca urmare, fixând vectorul x si notând ![]() coordonatele unui
vector oarecare din V, atunci:
coordonatele unui
vector oarecare din V, atunci:
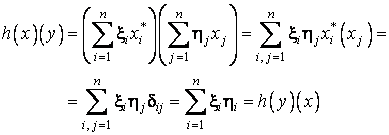
si, analog,
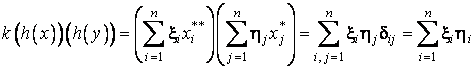 .
.
Asadar,
considerând în locul vectorului arbitrar ![]() vectorul
vectorul ![]() obtinem:
obtinem: ![]() . Q.E.D.
. Q.E.D.
Observatie
Pot exista transformari de baza pentru care izomorfismul h ramâne invariant. Dar iata o transformare de baza care schimba acest izomorfism.
Consideram
schimbarea de baza pentru care matricea de trecere este ![]() , cu
, cu ![]() . Cum coordonatele se transforma cu matricea
. Cum coordonatele se transforma cu matricea ![]() înseamna ca
noile coordonate ale lui x si y vor fi
înseamna ca
noile coordonate ale lui x si y vor fi ![]() , respectiv
, respectiv ![]() astfel ca în timp
ce în vechea baza
astfel ca în timp
ce în vechea baza 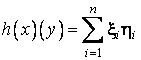 , în noua baza vom avea
, în noua baza vom avea 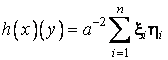 .
.
L.VI.1.2 Matricea unei forme biliniare
Forme biliniare
Fie
V un spatiu vectorial peste
corpul comutativ K. Se numeste forma biliniara pe spatiul V
o functie ![]() având urmatoarele
proprietati:
având urmatoarele
proprietati:
![]()
![]()
![]()
![]() .
.
Ca si forma liniara, forma biliniara este o functie scalara, adica ia valori scalare. Dar spre deosebire de forma liniara, cea biliniara depinde de doua variabile vectoriale.
Primele doua proprietati exprima faptul ca daca se fixeaza variabila (vectoriala) x, se obtine o forma liniara în y. Din urmatoarele doua rezulta ca daca se fixeaza y, se obtine o forma liniara în variabila x. Tocmai pentru ca este liniara în ambele variabile se numeste biliniara.
Exemple
1. Fie ![]() si A o matrice patratica de
ordinul n. Daca x si y sunt vectori, adica matrice coloana, atunci notând
si A o matrice patratica de
ordinul n. Daca x si y sunt vectori, adica matrice coloana, atunci notând ![]() transpusa matricei x, aceasta va fi o matrice linie, iar
produsul de matrice
transpusa matricei x, aceasta va fi o matrice linie, iar
produsul de matrice ![]() va fi o matrice având
o singura linie si o singura coloana, adica va fi un
scalar. Din proprietatile operatiilor cu matrice rezulta
ca sunt îndeplinite proprietatile din definitia formei
biliniare. Asadar orice matrice patratica de ordinul n defineste o forma
biliniara pe spatiul
va fi o matrice având
o singura linie si o singura coloana, adica va fi un
scalar. Din proprietatile operatiilor cu matrice rezulta
ca sunt îndeplinite proprietatile din definitia formei
biliniare. Asadar orice matrice patratica de ordinul n defineste o forma
biliniara pe spatiul ![]() .
.
2. Fie V = ![]() spatiul
vectorial real al functiilor reale continnue definite pe intervalul
spatiul
vectorial real al functiilor reale continnue definite pe intervalul ![]() si, pentru orice
pereche f si g de vectori din V
si, pentru orice
pereche f si g de vectori din V ![]() ,
,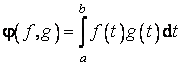 . Din proprietatile de calcul ale integralelor
definite rezulta ca sunt îndeplinite proprietatile din
definitia formei biliniare.
. Din proprietatile de calcul ale integralelor
definite rezulta ca sunt îndeplinite proprietatile din
definitia formei biliniare.
Matricea unei forme biliniare într-o baza data
Fie
![]() o baza a spatiului V si
o baza a spatiului V si ![]() o forma
biliniara pe spatiul V.
Matricea A care are pe linia i si coloana j scalarul
o forma
biliniara pe spatiul V.
Matricea A care are pe linia i si coloana j scalarul ![]()
![]() se numeste matricea
formei biliniare φ în baza
se numeste matricea
formei biliniare φ în baza ![]() .
.
Folosind
aceasta matrice se poate exprima valoarea lui ![]() în functie de
coordonatele vectorilor x si y. Într-adevar, fie
în functie de
coordonatele vectorilor x si y. Într-adevar, fie ![]() coordonatele lui x si
coordonatele lui x si ![]() coordonatele lui y în baza
coordonatele lui y în baza ![]() . Biliniaritatea lui φ înseamna ca φ se
distribuie fata de suma, adica poate comuta cu
operatia de sumare si, în cadrul fiecarui termen, scalarii pot
trece în fata lui φ. Deci:
. Biliniaritatea lui φ înseamna ca φ se
distribuie fata de suma, adica poate comuta cu
operatia de sumare si, în cadrul fiecarui termen, scalarii pot
trece în fata lui φ. Deci:

Putem
folosi si scrierea concentrata: ![]() unde, amintim,
unde, amintim, ![]() .
.
Observam
ca daca ![]() , pentru orice x si y, atunci
, pentru orice x si y, atunci ![]() . Într-adevar, înlocuind în relatia
. Într-adevar, înlocuind în relatia ![]() pe x cu xi
si y cu
pe x cu xi
si y cu ![]() , toti
, toti ![]() sunt nuli în
afara de
sunt nuli în
afara de ![]() care este egal cu 1 si
toti
care este egal cu 1 si
toti ![]() sunt nuli în
afara de
sunt nuli în
afara de ![]() care este egal cu 1.
Ca urmare în suma
care este egal cu 1.
Ca urmare în suma ![]() un singur termen
este nenul si anume cel care corespunde perechii de indici i si j, astfel ca
un singur termen
este nenul si anume cel care corespunde perechii de indici i si j, astfel ca ![]()
Formula
de transformare a matricei unei forme biliniare
la schimbarea bazei
Fie
![]() o noua baza
a lui V,
o noua baza
a lui V, ![]() coordonatele lui x si
coordonatele lui x si ![]() coordonatele lui y în aceasta baza. Notam
coordonatele lui y în aceasta baza. Notam ![]() matricea de
trecere de la baza
matricea de
trecere de la baza ![]() la baza
la baza ![]() .
.
Ne
propunem sa calculam matricea ![]() a formei biliniare
φ în noua baza în functie de matricele A si T. Pentru
aceasta este suficient sa exprimam
a formei biliniare
φ în noua baza în functie de matricele A si T. Pentru
aceasta este suficient sa exprimam ![]() în functie de
coordonatele noi
în functie de
coordonatele noi ![]() si
si ![]() . Ţinând seama ca:
. Ţinând seama ca: ![]() si
si ![]() rezulta:
rezulta:
![]() adica
adica
![]()
Reamintim
în acest context ca formula de transformare a matricei unui operator
liniar la schimbarea bazei este ![]() .
.
L.VI.1.3 Forme biliniare simetrice; forme patratice
Forma
biliniara ![]() se numeste simetrica daca, pentru orice
pereche de vectori x si y,
se îndeplineste conditia:
se numeste simetrica daca, pentru orice
pereche de vectori x si y,
se îndeplineste conditia: ![]() .
.
Propozitie
Forma biliniara φ este simetrica daca si numai daca matricea sa într-o baza oarecare este simetrica.
Demonstratie
Fie ![]() matricea formei
matricea formei ![]() în baza
în baza ![]() .
.
Presupunem ca forma ![]() este simetrica.
Atunci, cum pentru orice pereche de vectori x
si y se îndeplineste
conditia:
este simetrica.
Atunci, cum pentru orice pereche de vectori x
si y se îndeplineste
conditia: ![]() , rezulta în particular ca:
, rezulta în particular ca:
![]() ,
,
adica matricea A este simetrica.
Sa mai
observam ca daca matricea A
a unei forme biliniare ![]() într-o baza
oarecare este simetrica, adica
într-o baza
oarecare este simetrica, adica ![]() atunci ea este simetrica în orice
alta baza. Într-adevar, daca matricea de trecere la o
noua baza este T, atunci
matricea formei
atunci ea este simetrica în orice
alta baza. Într-adevar, daca matricea de trecere la o
noua baza este T, atunci
matricea formei ![]() în noua baza este
:
în noua baza este
:
![]() .
.
Reciproc,
sa presupunem ca matricea A
este simetrica, adica ![]() si sa
notam
si sa
notam ![]() , respectiv
, respectiv ![]() coordonatele a doi vectori oarecare x si y. Remarcând
ca orice matrice patratica de ordinul unu este simetrica
si ca
coordonatele a doi vectori oarecare x si y. Remarcând
ca orice matrice patratica de ordinul unu este simetrica
si ca ![]() se obtine:
se obtine:
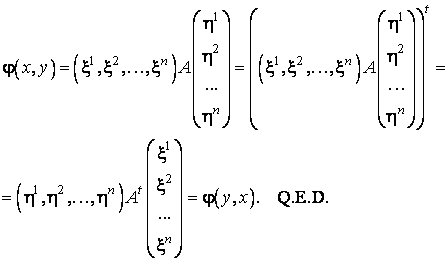
Forme patratice
Daca
în expresia unei forme biliniare: ![]() înlocuim pe y cu x
obtinem:
înlocuim pe y cu x
obtinem: ![]() , adica un polinom
omogen de gradul doi în coordonatele
, adica un polinom
omogen de gradul doi în coordonatele ![]() ale vectorului
variabil x, care se numeste forma
patratica.
ale vectorului
variabil x, care se numeste forma
patratica.
Ne
punem problema daca din expresia unei forme patratice (un polinom
omogen de gradul doi în ![]() ) putem sa recuperam forma biliniara din
care a provenit, mai precis matricea formei biliniare. Este suficient de
relevant sa efectuam aceasta analiza pentru cazul
) putem sa recuperam forma biliniara din
care a provenit, mai precis matricea formei biliniare. Este suficient de
relevant sa efectuam aceasta analiza pentru cazul ![]() . Expresia formei
biliniare este:
. Expresia formei
biliniare este:
![]() , iar forma patratica dedusa din aceasta este
, iar forma patratica dedusa din aceasta este ![]() .
.
![]() ,
,
adica presupunem cunoscuti
coeficientii ![]() si ne propunem sa determinam elementele
matricei formei biliniare. Pentru aceasta dispunem de trei ecuatii:
si ne propunem sa determinam elementele
matricei formei biliniare. Pentru aceasta dispunem de trei ecuatii:
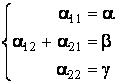 .
.
Se
vede ca elementele de pe diagonala matricei sunt determinate: ele sunt
coeficientii patratelor. Pentru ![]() este cunoscuta
numai suma lor.
este cunoscuta
numai suma lor.
Deci exista o infinitate de forme biliniare care determina aceeasi forma patratica.
Dar daca forma
biliniara este simetrica, atunci ea este determinata: ![]() .
.
Acest
lucru este valabil si pe cazul general, adica pentru n oarecare: exista o infinitate de forme biliniare care determina
aceeasi forma patratica, dar dintre acestea numai una este
simetrica. Când vorbim de matricea unei forme patratice
întelegem matricea formei biliniare simetrice atasate. Ea se
alcatuieste astfel: elementele de pe diagonala sunt
coeficientii patratelor; elementul de pe linia i si coloana j
este egal cu elementul de pe linia j si coloana i si este egal cu jumatatea
coeficientului lui ![]() .
.
La fel ca si în cazul operatorilor liniari, pornind de la faptul ca matricea unei forme biliniare depinde de baza, ne propunem sa gasim o baza în care aceasta matrice sa aiba forma diagonala.
Spre deosebire de cazul operatorilor liniari, de asta data problema are întotdeauna solutie. Ne vom ocupa însa de rezolvarea acestei probleme numai pentru cazul formelor simetrice, adica de fapt al formelor patratice. Solutia acestei probleme pentru cazul formelor patratice este utila în dezvoltarea ulterioara.
Sa
observam mai întâi ca, data fiind semnificatia matricei
unei forme patratice, gasirea unei baze în care aceasta matrice
sa fie o matrice diagonala echivaleaza prin rescrierea formei
patratice, astfel încât ea sa apara ca suma numai de
patrate cu diversi coeficienti, adica sa nu mai
aiba nici un termen mixt, cum ar fi ![]() .
.
În consecinta în loc de "gasirea unei baze în care matricea formei patratice sa fie o matrice diagonala" putem spune "aducerea formei patratice la o suma de patrate".
L.VI.1.4 Metoda lui Gauss pentru aducerea unei forme patratice la o suma de patrate
Consideram
forma patratica 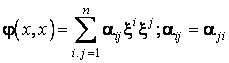 ; în care variabilele
; în care variabilele ![]() sunt coordonatele
vectorului variabil x în baza
sunt coordonatele
vectorului variabil x în baza![]() a spatiului vectorial V peste corpul comutativ K.
Presupunem ca
a spatiului vectorial V peste corpul comutativ K.
Presupunem ca ![]() , coeficientul lui
, coeficientul lui ![]() este nenul si îl
vom numi în continuare pivot.
este nenul si îl
vom numi în continuare pivot.
Prelucram din
suma ![]() partea
constituita din termenii care contin variabila
partea
constituita din termenii care contin variabila ![]() tinând seama
ca
tinând seama
ca ![]()
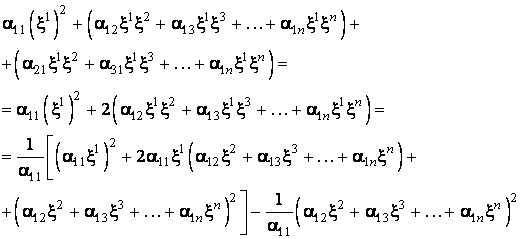
Rezulta:
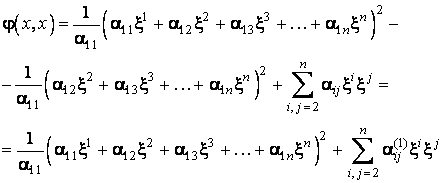
Sa
calculam coeficientii ![]() ai noii forme în care nu mai apare
ai noii forme în care nu mai apare![]() :
:
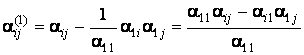 .
.
Observam
ca numaratorul din expresia lui ![]() se calculeaza
dupa "regula dreptunghiului". Asadar, în ipoteza ca
se calculeaza
dupa "regula dreptunghiului". Asadar, în ipoteza ca ![]() am scris forma
patratica sub forma de patrat al unei forme liniare
înmultita cu un scalar, la care se adauga o forma
patrata cu mai putine variabile: dintre ele lipseste
am scris forma
patratica sub forma de patrat al unei forme liniare
înmultita cu un scalar, la care se adauga o forma
patrata cu mai putine variabile: dintre ele lipseste ![]() . Forma liniara din paranteza are drept
coeficienti elementele de pe prima linie a matricei A.
. Forma liniara din paranteza are drept
coeficienti elementele de pe prima linie a matricei A.
Coeficientii
formei patratice ramase (din care lipseste ![]() ) se calculeaza dupa regula dreptunghiului însotita de împartirea
la pivot.
) se calculeaza dupa regula dreptunghiului însotita de împartirea
la pivot.
Ceea
ce s-a facut cu forma patratica initiala se poate face
cu forma patratica obtinuta: în ipoteza ca ![]() , alegându-l pe acesta drept pivot, se scrie sub forma
urmatoare: inversul pivotului înmultit cu patratului formei
liniare având drept coeficienti elementele primei linii a matricei formei
patratice la care se adauga o forma patratica în care
nu mai apare nici
, alegându-l pe acesta drept pivot, se scrie sub forma
urmatoare: inversul pivotului înmultit cu patratului formei
liniare având drept coeficienti elementele primei linii a matricei formei
patratice la care se adauga o forma patratica în care
nu mai apare nici ![]() nici
nici ![]() . Se transforma în continuare noua forma
patratica obtinuta si asa mai departe.
. Se transforma în continuare noua forma
patratica obtinuta si asa mai departe.
Asadar, dupa n transformari (iteratii), în ipoteza ca de fiecare data elementul de pe prima linie si prima coloana a matricei formei patratice obtinute este nenul, forma patratica devine o suma de patrate de forme liniare, aceste patrate fiind înmultite cu diversi coeficienti:
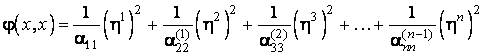 ,
,
în care:
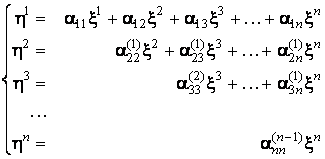 .
.
Deoarece
![]() sunt expresii liniare
depinzând de
sunt expresii liniare
depinzând de ![]() , ele constituie coordonatele vectorului variabil x într-o noua baza,
, ele constituie coordonatele vectorului variabil x într-o noua baza, ![]() . Notând, ca de obicei, cu T matricea de trecere de la baza
. Notând, ca de obicei, cu T matricea de trecere de la baza ![]() la baza
la baza ![]() putem scrie:
putem scrie:
 ,
,
din care, calculând
matricea T putem obtine noua
baza ![]() .
.
Sa
revenim acum asupra ipotezei ![]() . Daca
. Daca ![]() înseamna ca
lipseste termenul care contine monomul
înseamna ca
lipseste termenul care contine monomul ![]() . Presupunem ca în expresia formei patratice
exista un patrat având coeficientul nenul, altfel spus, diagonala
matricei are cel putin un element nenul, fie acesta
. Presupunem ca în expresia formei patratice
exista un patrat având coeficientul nenul, altfel spus, diagonala
matricei are cel putin un element nenul, fie acesta ![]() .
.
Înlocuind: ![]() (
(![]() vor fi coor-donatele vectorului variabil x într-o noua baza, si
anume
vor fi coor-donatele vectorului variabil x într-o noua baza, si
anume ![]() ), matricea formei patratice va
avea pe locul de pe prima linie si prima coloana elementul
), matricea formei patratice va
avea pe locul de pe prima linie si prima coloana elementul ![]() coeficientul lui
coeficientul lui ![]() coeficientul lui
coeficientul lui ![]() . Luându-l pe acesta drept pivot se poate efectua
transformarea descrisa.
. Luându-l pe acesta drept pivot se poate efectua
transformarea descrisa.
Presupunem
ca forma patratica nu contine nici un patrat,
adica toate elementele de pe diagonala matricei sunt nule. Presupunem
totusi ca matricea are cel putin un element nenul în afara
diagonalei, fie acesta ![]() .
.
Trecând la noile
coordonate ![]() , definite de:
, definite de:
![]() ,
,
matricea formei patratice în noile coordonate va avea elementul de pe prima linie si prima coloana nenul.
Este
posibil ca, dupa ![]() iteratii,
forma patratica ramasa sa fie nula. Atunci forma
patratica va avea, fireste, numai r patrate. Primele r
dintre coordonatele
iteratii,
forma patratica ramasa sa fie nula. Atunci forma
patratica va avea, fireste, numai r patrate. Primele r
dintre coordonatele ![]() se definesc prin
formulele de mai sus, iar celelalte se pot lua egale cu coordonatele
corespunzatoare
se definesc prin
formulele de mai sus, iar celelalte se pot lua egale cu coordonatele
corespunzatoare ![]() . Numarul r se
numeste rangul formei patratice.
El este egal cu rangul matricei A a
formei, deoarece pe de o parte matricea B
a formei în noua baza va avea primele r
elemente de pe diagonala egale cu cei r
coeficienti nenuli, iar celelalte elemente ale matricei sunt nule astfel
ca
. Numarul r se
numeste rangul formei patratice.
El este egal cu rangul matricei A a
formei, deoarece pe de o parte matricea B
a formei în noua baza va avea primele r
elemente de pe diagonala egale cu cei r
coeficienti nenuli, iar celelalte elemente ale matricei sunt nule astfel
ca ![]() . Pe de alta parte, notând cu T matricea de trecere la noua baza, acesta este
inversabila si
. Pe de alta parte, notând cu T matricea de trecere la noua baza, acesta este
inversabila si ![]() , astfel ca
, astfel ca ![]() .
.
Exemple
1. Sa se aduca la o suma de patrate forma patratica:
![]() ,
,
în care ![]() sunt coordonatele
vectorului variabil
sunt coordonatele
vectorului variabil ![]() în baza canonica.
în baza canonica.
Rezolvare
Scriem matricea A a formei patratice careia-i aplicam transformarile (iteratiile) corespunzatoare:
![]()
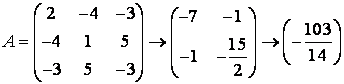 .
.
De fiecare data se transforma blocul obtinut prin excluderea primei linii si coloane, în care se afla pivotul. Elementele blocului se transforma cu regula dreptunghiului urmata de împartirea la pivot. De exemplu, primul element al blocului se transforma astfel:
![]() .
.
Se obtine urmatoarea expresie a formei patratice:
![]() ,
,
în care:
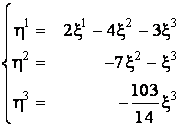 ,
,
din care se poate scrie matricea de transformare a coordonateelor:
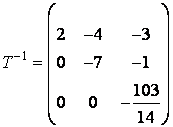 si deci
si deci 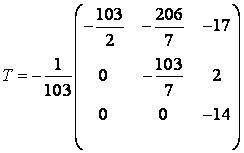 .
.
Coloanele matricei T constituie vectorii noii baze.
2.
Aducem la o suma de patrate prin metoda lui Gauss urmatoarea
forma patratica din ![]() :
:
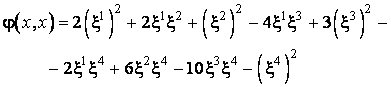

Dupa prima iteratie matricea obtinuta are elementul de pe prima linie si prima coloana egal cu zero, deci acest element nu poate juca rolul pivotului.
Forma patratica a devenit:
![]() ,
,
adica patratul formei liniare având
drept coeficienti elementele primei linii a matricei A plus o forma patratica în ![]() a carei matrice
este
a carei matrice
este ![]() .
.
Efectuam urmatoarea transformare de coordonate:
![]() . Înlocuind
. Înlocuind ![]() în functie de
în functie de ![]() forma
patratica devine:
forma
patratica devine:
![]() .
.
Matricea
B a formei în ![]() are primul element
nenul si deci ei i se pot aplica transformarile respective:
are primul element
nenul si deci ei i se pot aplica transformarile respective:
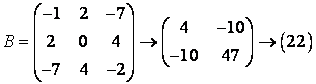
Deci:
![]() ,
,
unde:
 .
.
3. Aducem la o suma de patrate forma patratica:
![]() .
.
Forma nu contine nici un patrat, matricea formei are toate elementele de pe diagonala egale cu zero.
Efectuam
urmatoarea transformare: ![]() . Înlocuind în forma patratica, aceasta devine:
. Înlocuind în forma patratica, aceasta devine:
![]() .
.
 Matricei B a formei i se pot aplica
transformarile respective:
Matricei B a formei i se pot aplica
transformarile respective:
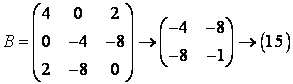
Asadar,
![]()
unde:
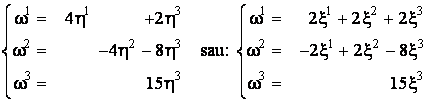
L.VI.1.5 Metoda lui Iacobi
În anumite conditii se poate aplica si o alta metoda care cu aspect mai sintetic.
Teorema
Fie
![]() matricea unei forme
patratice
matricea unei forme
patratice ![]() în baza
în baza ![]() a spatiului
vectorial V si pentru orice
a spatiului
vectorial V si pentru orice ![]() sa notam
sa notam ![]() minorul matricei A format cu primele r linii si coloane;
minorul matricei A format cu primele r linii si coloane; ![]() .
.
Daca toti
acesti minori sunt nenuli, atunci exista o baza ![]() în care expresia
formei patratice este:
în care expresia
formei patratice este:
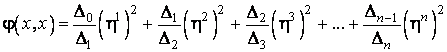 .
.
Demonstratie
Pentru fiecare r vectorul ![]() îl cautam de
forma:
îl cautam de
forma: ![]()
![]()
![]() . Determinam coeficientii
. Determinam coeficientii ![]() astfel ca vectorul
astfel ca vectorul ![]() sa înde-plineasca urmatoarele
conditii:
sa înde-plineasca urmatoarele
conditii: ![]()
![]() .,
., ![]()
![]() .
.
Ţinând
seama de linearitatea formei ![]() în prima
variabila si de faptul ca
în prima
variabila si de faptul ca ![]() conditiile impuse
vectorului
conditiile impuse
vectorului ![]() revin la sistemul
liniar:
revin la sistemul
liniar:
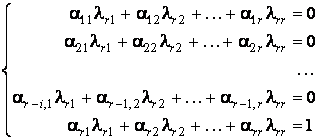 .
.
Sistemul
are r ecuatii cu tot r necunoscute, iar determinantul
matricei coeficientilor este tocmai ![]() despre care stim
prin ipoteza ca este nenul.
despre care stim
prin ipoteza ca este nenul.
Prin urmare sistemul
este compatibil si chiar determinat. Observam în plus ca,
potrivit regulii lui Cramer, 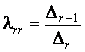 .
.
Ramâne
sa demonstram ca vectorii ![]() formeaza o
baza si ca aceasta baza îndeplineste
conditia din enuntul teoremei.
formeaza o
baza si ca aceasta baza îndeplineste
conditia din enuntul teoremei.
Matricea
coordonatelor vectorilor ![]() este
triunghiulara având pe diagonala elementele
este
triunghiulara având pe diagonala elementele ![]() care sunt nenule. Prin
urmare determinantul acestei matrici este nenul, de unde rezulta ca
vectorii
care sunt nenule. Prin
urmare determinantul acestei matrici este nenul, de unde rezulta ca
vectorii ![]() constituie o
baza.
constituie o
baza.
Sa
notam ![]() matricea formei
patratice în baza
matricea formei
patratice în baza ![]() .
.
Pentru ![]()
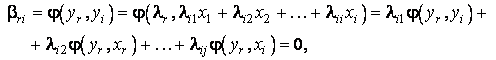
deoarece
![]() .
.
Din cauza simetriei
matricei B deducem ca si
pentru ![]() avem
avem ![]() , adica matricea B
este o matrice diagonala.
, adica matricea B
este o matrice diagonala.
Elementele de pe diagonala sunt:
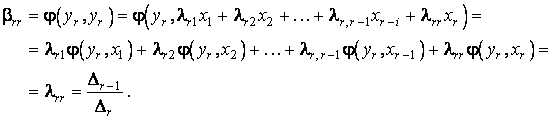
Din
definitia matricei unei forme patratice rezulta ca expresia
formei
patratice este cea din enunt. Q.E.D.
Exemplu
Vom folosi metoda rezultata din teorema lui Iacobi pentru a aduce la o suma de patrate forma patratica:
![]() ,
,
în care ![]() sunt coordonatele
vectorului variabil
sunt coordonatele
vectorului variabil ![]() în baza canonica.
în baza canonica.
Matricea formei este:
 ,
,
din care rezulta: ![]() toti nenuli,
astfel încât se poate aplica metoda Iacobi. Expresia formei patratice
este:
toti nenuli,
astfel încât se poate aplica metoda Iacobi. Expresia formei patratice
este:
![]() ,
,
în care ![]() sunt coordonatele
vectorului variabil x într-o
noua baza,
sunt coordonatele
vectorului variabil x într-o
noua baza,
![]() .
.
Vectorii ![]() constituie baza
canonica, iar coeficientii
constituie baza
canonica, iar coeficientii ![]() se determina din
sistemele:
se determina din
sistemele:
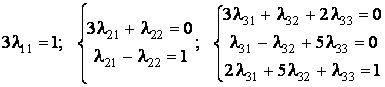 .
.
Rezolvând sistemele se obtine:
![]() .
.
L.VI.1.6 Teorema inertiei (Sylvester)
Cunoscând faptul ca exista mai multe metode de aducere a unei forme patratice la o suma de patrate se pune problema în ce masura pot sa difere rezultatele daca aceeasi forma patratica este adusa la o suma de patrate prin doua metode diferite.
Am remarcat deja ca numarul coeficientilor nenuli nu poate sa depinda de metoda. Acest numar a fost numit rangul formei. El este rangul matricei formei într-o baza oarecare, care rang nu se schimba daca se schimba baza.
Pentru a gasi alti invarianti ai formelor patratice trebuie sa facem o restrictie asupra corpului de scalari. Mai precis, obiectul teoremei care urmeaza este cel al spatiilor vectoriale reale, adica acelea în care corpul de scalari este corpul numerelor reale.
Teorema
Fie
V un spatiu vectorial real finit
generat si ![]() o forma
patratica definita pe acest spatiu. Daca forma este
adusa la o suma de patrate prin doua metode diferite,
atunci numarul coeficientilor pozitivi, negativi si nuli, în
cele doua rezultate, este acelasi.
o forma
patratica definita pe acest spatiu. Daca forma este
adusa la o suma de patrate prin doua metode diferite,
atunci numarul coeficientilor pozitivi, negativi si nuli, în
cele doua rezultate, este acelasi.
Demonstratie
Folosind una din
metode, se ajunge la o baza ![]() în care expresia
formei patratice este:
în care expresia
formei patratice este:
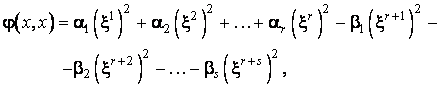
în care ![]() sunt coordonatele
vectorului variabil x în baza
sunt coordonatele
vectorului variabil x în baza ![]() , iar
, iar ![]() sunt numere reale
strict pozitive si
sunt numere reale
strict pozitive si ![]() . Asadar forma are r
coeficienti strict pozitivi, s
sunt strict negativi, iar restul, pâna la n, sunt nuli.
. Asadar forma are r
coeficienti strict pozitivi, s
sunt strict negativi, iar restul, pâna la n, sunt nuli.
Folosind
o alta metoda, se ajunge la baza ![]() în care expresia
aceleiasi forme patratice este:
în care expresia
aceleiasi forme patratice este:
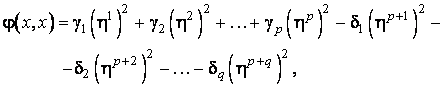
în care ![]() sunt noile coordonate
ale lui x, iar
sunt noile coordonate
ale lui x, iar ![]() sunt numere reale
strict pozitive si, fireste,
sunt numere reale
strict pozitive si, fireste, ![]() . Altfel spus, prin aceasta metoda s-au
obtinut p coeficienti
strict pozitivi, q strict negativi,
iar restul pâna la n sunt nuli.
. Altfel spus, prin aceasta metoda s-au
obtinut p coeficienti
strict pozitivi, q strict negativi,
iar restul pâna la n sunt nuli.
Vrem
sa demonstram ca ![]() .
.
Presupunem, prin reducere la absurd, ca ![]() . Sunt atunci posibile doua situatii: sau
. Sunt atunci posibile doua situatii: sau ![]() . Alegem prima varianta, adica
. Alegem prima varianta, adica ![]() .
.
Consideram
sirul de vectori:![]() . Numarul lor este
. Numarul lor este ![]() care este strict mai
mare decât dimensiunea n a
spatiului V în ipoteza ca
care este strict mai
mare decât dimensiunea n a
spatiului V în ipoteza ca ![]() . Prin urmare acesti vectori nu pot fi liniar
independenti.
. Prin urmare acesti vectori nu pot fi liniar
independenti.
Exista deci
scalarii: ![]() nu toti nuli, astfel încât:
nu toti nuli, astfel încât:
![]() .
.
Cel
putin unul dintre scalarii ![]() este nenul. În caz
contrar am avea o combinatie liniara nula a vectorilor
este nenul. În caz
contrar am avea o combinatie liniara nula a vectorilor ![]() , care constituie o baza, de unde ar rezulta ca
toti coeficientii acestei combinatii liniare ar fi nuli, deci
odata cu coeficientii
, care constituie o baza, de unde ar rezulta ca
toti coeficientii acestei combinatii liniare ar fi nuli, deci
odata cu coeficientii ![]() devin nuli si
coeficientii
devin nuli si
coeficientii ![]() .
.
Notam
![]() . Din relatia de mai sus rezulta:
. Din relatia de mai sus rezulta: ![]() . Am obtinut aici scrierea lui
. Am obtinut aici scrierea lui ![]() atât ca o
combinatie liniara de
atât ca o
combinatie liniara de ![]() , cât si ca o combinatie liniara de
, cât si ca o combinatie liniara de ![]() . Mai precis, pentru vectorul
. Mai precis, pentru vectorul ![]() avem, pe de o
parte:
avem, pe de o
parte:
![]() ,
,
iar pe de alta parte:
![]() .
.
Folosind prima expresie a lui φ obtinem:
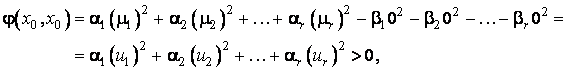
deoarece toti coeficientii ![]() sunt strict pozitivi
si cel putin unul dintre coeficientii
sunt strict pozitivi
si cel putin unul dintre coeficientii ![]() este nenul.
este nenul.
Folosind a doua expresie a lui φ obtinem:
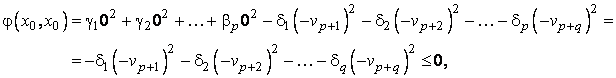 deoarece toti coeficientii
deoarece toti coeficientii ![]() sunt strict pozitivi.
sunt strict pozitivi.
Am
ajuns astfel la o contradictie care provine din ipoteza ca ![]() . La fel se înlatura si ipoteza ca
. La fel se înlatura si ipoteza ca![]() . Asadar
. Asadar![]() . Analog se demonstreaza ca
. Analog se demonstreaza ca ![]() . Q.E.D.
. Q.E.D.
Forme patratice pozitiv definite
O
forma patratica ![]() definita pe un
spatiu vectorial real se numeste pozitiv
definita daca fiind adusa la o suma de patrate,
toti coeficientii patratelor sunt strict pozitivi.
definita pe un
spatiu vectorial real se numeste pozitiv
definita daca fiind adusa la o suma de patrate,
toti coeficientii patratelor sunt strict pozitivi.
Teorema anterioara ne asigura ca nu întâlnim ambiguitati în a decide daca o forma este sau nu pozitiv definita (altfel spus ca definitia este "consistenta"). Într-adevar, daca folosind o metoda de aducere la o suma de patrate forma obtinuta are n coeficienti strict pozitivi, atunci la fel se va întâmpla daca folosim orice alta metoda.
Propozitie
O
forma patratica ![]() a unui spatiu
real V de dimensiune n este pozitiv definita daca
si numai daca exista o baza în care matricea formei este
matricea unitate
a unui spatiu
real V de dimensiune n este pozitiv definita daca
si numai daca exista o baza în care matricea formei este
matricea unitate ![]() .
.
Demonstratie
Evident
ca daca matricea lui ![]() într-o baza este
matricea unitate, atunci
într-o baza este
matricea unitate, atunci ![]() este pozitiv
definita. Reciproc, sa presupunem ca forma
este pozitiv
definita. Reciproc, sa presupunem ca forma ![]() este pozitiv
definita. Exista atunci o baza
este pozitiv
definita. Exista atunci o baza ![]() în care expresia
formei patratice este
în care expresia
formei patratice este ![]() cu toti
coeficientii
cu toti
coeficientii ![]() strict pozitivi.
Notând
strict pozitivi.
Notând ![]() expresia formei
patratice devine:
expresia formei
patratice devine:
![]() .
.
Matricea formelor liniare ![]() este o matrice
diagonala cu elementele de pe diagonala, deci o matrice
inversabila. Asadar
este o matrice
diagonala cu elementele de pe diagonala, deci o matrice
inversabila. Asadar ![]() reprezinta
coordonatele vectorului variabil x
într-o alta baza. În aceasta noua baza matricea formei
reprezinta
coordonatele vectorului variabil x
într-o alta baza. În aceasta noua baza matricea formei
![]() este matricea
este matricea ![]() . Q.E.D.
. Q.E.D.
L.VI.1.7 PROBLEME PROPUSE
PP.VI.1.7.1 Fie ![]() spatiul vectorial
al polinoamelor de grad cel mult
spatiul vectorial
al polinoamelor de grad cel mult ![]() cu coeficienti
reali, de variabila reala
cu coeficienti
reali, de variabila reala ![]() ,
, ![]() un numar real
fixat si aplicatia:
un numar real
fixat si aplicatia: ![]() definita prin:
definita prin: ![]() .
.
a)
Sa se arate ca ![]() este forma
liniara pe
este forma
liniara pe ![]() ;
;
b) Sa se afle
care sunt formele liniare pe ![]() pentru care
exista un un numar
pentru care
exista un un numar ![]() astfel încât valoarea
formei liniare în
astfel încât valoarea
formei liniare în ![]() sa fie
sa fie ![]() .
.
PP.VI.1.7.2 Se considera forma biliniara: ![]() , definita prin:
, definita prin: ![]() . Sa se scrie matricea sa asociata:
. Sa se scrie matricea sa asociata:
a) în baza canonica;
b) în baza ![]() , unde:
, unde: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
PP.VI.1.7.3 Sa se precizeze
care din urmatoarele functii sunt forme biliniare si în caz
afirmativ sa se gaseasca matricea si rangul formei si spatiul
nul relativ la al doilea argument. (Fie ![]() este o forma
biliniara. Multimea vectorilor
este o forma
biliniara. Multimea vectorilor ![]() formeaza un
subspatiu liniar al lui
formeaza un
subspatiu liniar al lui ![]() numit spatiul
nul al lui
numit spatiul
nul al lui ![]() relativ la al doilea
argument.):
relativ la al doilea
argument.):
a) ![]() ,
, 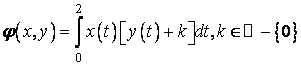 ;
;
b) ![]() ,
, ![]() .
.
PP.VI.1.7.4 Se da forma patratica: ![]() ,
, ![]() .
.
a) Sa se scrie matriceal si sa se determine rangul formei;
b) Sa se gaseasca expresia canonica prin metoda Gauss si sa se stabileasca matricea de trecere.
PP.VI.1.7.5 Se considera
forma patratica: ![]() ,
, ![]() ;
;
a) Sa se reduca la forma canonica prin metoda lui Gauss si sa se determine si baza în care are loc forma canonica;
b) Sa se reduca la forma canonica prin metoda lui Jacobi si sa se determine baza si formulele de schimbare a coordonatelor.
L.VI.1.8 TEST DE AUTOEVALUARE
TAev.VI.1.8.1 Fie ![]() vectori din
vectori din ![]() .
.
a) Sa se arate
ca exista o singura forma liniara ![]() , astfel încât:
, astfel încât: ![]() ;
;
b) Sa se
determine dimensiunea si o baza a subspatiului ![]() .
.
TAev.VI.1.8.2 Fie ![]() spatiul vectorial
al functiilor polinomiale reale care au cel mult gradul trei si fie
spatiul vectorial
al functiilor polinomiale reale care au cel mult gradul trei si fie ![]() aplicatia
definita prin:
aplicatia
definita prin: 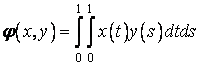 .
.
a) Sa se arate
ca ![]() este o forma biliniara;
este o forma biliniara;
b) Sa se
determine matricea sa în baza canonica a spatiului si apoi
matricea sa în baza ![]() .
.
TAev.VI.1.8.3 Sa se precizeze care din urmatoarele functii sunt forme biliniare si în caz afirmativ sa se gaseasca matricea si rangul formei si spatiul nul relativ la al doilea argument (a se vedea problema nr. PP.VI.1.7.3):
a) ![]() ,
, ![]() ;
;
b)![]() ,
, ![]() .
.
TAev.VI.1.8.4 Se considera formele patratice:
1)
![]() ,
, ![]() ;
;
2)
![]() ,
, ![]() .
.
a) Sa se reduca la forma canonica prin metoda lui Gauss si sa se determine si baza în care are loc forma canonica;
b) Sa se reduca la forma canonica prin metoda lui Jacobi si sa se determine baza si formulele de schimbare a coordonatelor.
TAev.VI.1.8.5 Se dau urmatoarele forme patratice:
1) ![]() ,
, ![]() ;
;
2)
![]() ,
, ![]() ;
;
3)![]() ,
, ![]() .
.
Sa se gaseasca pentru fiecare o baza ortonormata fata de care forma patratica are o expresie canonica.
|