FUNCŢIONALE LINIARE; BILINIARE; FORME PĂTRATICE
Functionale liniare, functionale biliniare, forme patratice
Fie X/K spatiu vectorial
Definitie Se
numeste functionala o functie 
.
Definitie O
functionala se numeste liniara
daca 
Exemplu: 
Definitie Multimea 
se numeste spatiul
dual al lui X.
Observatie Cum K este spatiu vectorial peste corpul K o functionala liniara este de fapt un operator liniar.
Fie X/K, Y/K doua spatii liniare peste acelasi corp K.
Definitie Functionala 
se numeste functionala
biliniara daca este liniara în ambele argumente, adica:
si analog pentru variabila de pe pozitia a II-a, sau, echivalent cu cele 4 conditii din definitie:
Exemple:
Matricea functionalei biliniare în bazele E si G
Fie
o baza în X, 
o baza în Y.
Pentru
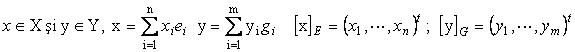
Fie
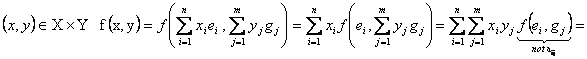
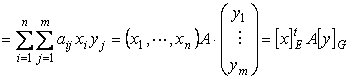
Definitie Matricea 
se numeste matricea
functionalei biliniare în bazele E si G.
Deci
Modificarea matricii unei functionale biliniare la schimbarea bazelor
În
X presupunem trecerea de la E la baza 
cu matricea 
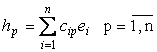
În Y analog de la
G la baza 
cu matricea 
=
=
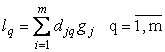
. Deci 
iar
Daca X=Y si E=G,
H=L rezulta 
Definitie O functionala
biliniara 
se numeste
simetrica daca 
Propozitie
f este o functionala biliniara
simetrica daca si numai daca matricea ei într-o baza a
lui X este simetrica i.e. 
.
Observatie: Cu
orice functionala biliniara 
se poate defini o
functionala biliniara simetrica 
Fie o
functionala biliniara simetrica.
Definitie Se numeste functionala patratica (forma patratica) restrictia unei functionale biliniare simetrice la diagonala produsului cartezian, D.
Daca
baza a lui X si 
, functionala
patratica devine: 
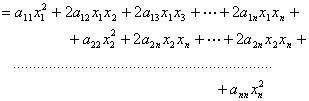
este matricea
atasata functionalei patratice V în baza E.
Functionala biliniara din care provine V, se numeste functionala polara a formei patratice V. Ea se obtine astfel:
deci 
Modificarea matricii unei functionale patratice la schimbarea bazei se face analog cu cea a unei functionale biliniare.
Fie
baza E G
matricea
atasata lui V în baza G
Definitie Despre o forma patratica spunem
ca are expresia canonica daca 
sau matricea atasata ei
are forma diagonala:
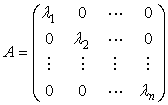
Baza în care are loc aceasta scriere se numeste o baza canonica pentru functionala V.
Aducerea la expresia canonica a unei forme patratice; procedee(metoda Gauss, Jacobi, vectorilor proprii);
Metoda Gauss
Pentru orice forma
patratica exista o baza canonica G în care forma ei
este 
cu 
. Fie exemplele:
a) Cazul 
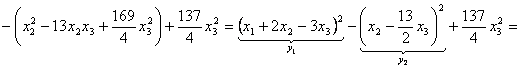
b) Cazul 
Fie forma patratica 
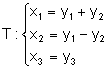Atunci cu
transformarea
; 
cu
transformarea: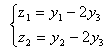
.
2) Metoda Jacobi
Teorema Daca în baza E forma patratica V are
matricea 
cu
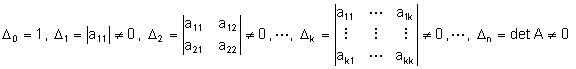
atunci exista o baza G în care forma patratica are expresia canonica data de:
cu
|
