GEOMETRIE ANALITICA

PUNTUL }I DREAPTA

CERCUL,ELIPSA,HIPERBOLA, ]i PARABOLA

SUBIECTE DE BACALAUREAT

PUNCTUL }[r1] I DREAPTA

1⁰ Distanta d dintre doua puncte M₁(x₁,y₁) ]i M₂(x₂,y₂) din plan este:

d=

2⁰ Coordonatele punctului P(x,y) care [mpart segmentul M₁M₂ [n raportul k : M₁P=k*PM₂ sunt x=, y= . Daca P este mijlocul segmentului M₁M₂ este P.

Coordonatele centrului de greutate G al triunghiului format de punctele P_i(x_I,y_I) I sunt G

x= , y=.

Ecuatiile unor drepte particulare din plan: x=0 (axa y^'oy) y=x(prima bisectoare)

y=0 (axa x'ox) y=-x(adoua bisectoare)

x=a (dreapta y'oy) y=m*x(trece prin O(0,0) )

y=b (dreapta x'ox)

Ecuatia generala a dreptei : Ax+By+C=0, A²+B²0

Ecuatia redusa a dreptei y=mx+n

Panta dreptei ce trece prin punctele M₁(x₁,y₁), M₂(x₂,y₂) m=

y ( C ) m =tg=f^'_(x)=lim

f_(x) xx₀

_q Daca f'_(x)=+(-) atunci tangenta este y'0y

₀ x₀  x

7⁰ Ecuatia dreptei care taie axele de coordonate [n A(a,0) si B(0,b) sau ecua\ia dreptei prin t`ieturi

8⁰ Ecuatia normala a dreptei : x cos a+y sin a - p=0 

9⁰ Ecuatia dreptei care trece prin P₀(x₀,y₀) ]i care are coeficientul unghiurilor m este :y-y₀=m(x-x₀)

10⁰ Ecuatia dreptei care trece prin doua puncte P₁(x₁,y₁) si P₂(x₂,y₂): sau sub forma de determinant:  x y 1

x₁ y₁ 1 =0

x₁ y₂ 1

11⁰ O condi\ie necesar` ca dreptele D<sub>1</sub> si D<sub>2</sub> s` fie parabole este m_D=m_D

12⁰ O condi\ie necesar` ca dreptele D<sub>1</sub> si D<sub>2</sub> s` fie perpendiculare este ca m_D= -

13⁰ Unghiul al dreptelor D₁ si D₂ de cceficienti unghiulari m₁, m₂ este dat de tg=

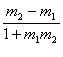
14⁰ Distanta d de la punctul P₀(x₀,y₀) la dreapta D : Ax+By+C=0 este d=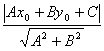

15⁰ Aria triunghiului determinat de M_I (x_I,y_I) I=1,2,3 este S= ,unde

D= x₁ y₁ 1

x₂ y₂ 1

x₃ y₃ 1

PROBLEME:

Este util ca rezolvarea oricarei probleme de geometrie s` inceap` cu desenarea figurilor corespunz`toare.

Un triunghi are varfurile :A(-2,-1), B(1,2), C(3,0)

a) S` se calculeze perimetrul triunghiului, aria triunghiului ,raza cercului inscris triunghiului,reza cercului circumscris triunghiului;

b)       S` se calculeze simetricul punctului B fat` de mijlocul segmentului AC.

R: a) Deoarece AC²=AB²+BC² conform reciprocei teoremei lui Pitagora mABC=90⁰

P=AB+AC+BC=2p, S= , r=, R=

b)       Fie B₁ simetricul lui B fat` de M , unde M mijlocul segmentului AC , M

x_M=

y_M= -

Coordonatele a dou` varfuri ale unui triunghi echilateral sunt (1,0) si (-1,0). S` se determine

coordonatele celui de-al treilea farf.

R: (0,) si (0,-)

Sa se caracterizeze patrulaterul de varfuri A(-5,4), B(3,5), C(7,-2), D(-1,-3);

R: m_AB=m_CD=, m_BC=m_AD= - ABCD paralelogram.

Dreapta d are panta 2 si contine punctul A(1,1) . S` se determine punctele lui d care se afl` la distanta 1 fat` de A

R: M₁( ), M₂()

Fiind dat` func\ia prin rela\ia f<sub>(x)</sub>=x<sup>2</sup>+x-3 s` se determine R astfel [ncat tangenta functiei [n punctul (2,f₍₂₎) s` fie paralel` cu prima bisectoare .

R: Calcul`m f'₍₂₎=lim =lim=lim

x2 x2 x2

Tangenta la graficul func\iei este paralel` cu prima bisectoare m=f'₍₂₎=1 =-3ecuatia tangentei in (2, f₍₂₎ ) este: y-f₍₂₎=f'₍₂₎(x-2) y-(-5)=1(x-2) x-y-7=0

Fiind date fuc\iile f_(x)=x²+x+2 , g_(x)=s` se determine astfel [nc@t graficele celor dou` fuc\ii s` aib` o tangent` comun` in punctul de abcis` 1

R: Se impun conditiile : f₍₁₎=g₍₁₎=0 si m=f'₍₁₎=g'₍₁₎sistemul obtinut este +2=0

=3, =-5 2=1

Se d` triunghiul de v@rfuri A(-1,3), B(2,-1). S` se g`seasc`:

a)       Ecua\ia dreptei AC

b)       Ecua\ia parabolei prin Bla AC

c)       Ecua\ia mediatoarei segmentului [BC]

d)       Ecua\ia medianei din C

e)       Ecua\ia [n`ltimii din C

R: a) m_AC=y-y_A=m_AC(x-x_AC)y=

b)       d₁|| AC m_d=m_AC=d₁: y=

c)       M mijlocul segmentului BC, M() d₂ , d₂ BC m_d=-=-

d₂: y=-

d) N mijlocul segmentului [AB], N() m_NC=2y-y_C=m_NC(x-x_c)y=2x

d)       CC₁ ABm_CC=- coliniare CAB dreptunghic [n A ecua\ia [n`l\imii din C este chiar AC: y=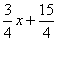

a) }tiind c` A(1,2) este piciorul perpendicularei duse din origine pe dreapta d, s` se scrie ecua\ia dreptei d

b)       S` se g`seasc` proiec\ia punctului B(-2,1) pe dreapta d: 2x+y+1=0

c)       S` se scrie ecua\ia dreptei ce trece prin C(1,3) ]i este echidistant de punctele M₁(-1,0), M₂(1,-1)

d)       S` se determine coordonatele simetricelor puntului D[-1,2) fa\` de dreapta d: x+y+1=0 ]i fa\` de E(-1,-4)

R: a) y=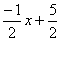 b) B₁=()

c) y= d) D'=(-3, 0) D''=(-1, -10)

9) S` se determine ecuatiile simetricelor dreptei d<sub>1</sub>: -x+2y-1=0 fa\` de dreapta d₂: x-y=0 ]i fa\` de

A(-2, 5)

R: d': 2x-4-1=0; d₃: 5x-10y+5=0

S` se scrie ecua\iile medianelor triungiului format de A(1,4) , B(3,-1) , C(8,-2). S` se demonstreze

c` centrul de greutate se afl` pe fiecare dintre ele.

R: 3x+y-7=0 ; y-1=0; x+2y-4=0 G(2,1)

11) Se dau punctele A(2,1) si (D) 2x-3y+1=0 , (D') x+2y-7=0. S` se determine punctul M de pe (D)

]tiind ca mijlocul segmentului AM se afl` pe (D')

R: M(4,3)

12) Dreptele d₁: x-3y+4=0 ]i d₂: 2x-y-5=0 determin` patru unghiuri .S` ae g`seasc` m`sura

unghiului al carui intereior con\ine 0(0,0)

R: m₁=, m₂=2, (0,)tg ==1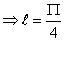

S` se calculeze lungimile [naltimilor ABC cu A(2,1), B(6,-1), C(4,4)

R: Scriem ecuatiile laturilor si calcul`m d(A,BC)==, d(B,AC)=

S` se calculeze aria ABCD , A(-2,2), B(-3,-1), C(-2,-3), D(2,0)

R: ABCD=ABC+ACD=

2.1 CERCUL =M/ CM=r , C(a,b)

Ecua\ia cercului C cu centrul in origine s] raza r este : ( 1 ) x²+y²-r² =0

Ecua\iile parametrice : x=r cos q, y=r sin q q[0,2p

Ecua\ia cu paratele str@nse este: ( 2 ) (x-a)² +(y-b)²-r²=0, (a,b) centrul, r raza

Ecua\iile parametrice : x=a+r cos q q[0,2p

Ecu\tia normal` a cercului este : x² + y² + mx + ny + p=0, a=, b=, si r²=

Ecua\ia general` a cercului este : A0, A (x²+y²) + Dx+ F=0

Ecua\ia patratic` a tangentelor la cercul ( 1 ) duse din punctul exterior P₀(x₀,y₀) este (r²-y₀²)( x-

x₀)²+2x₀y₀(x-x₀)(y-y₀)+(r²-x₀²)(y-y₀²)=0

Puterea a punctului P₀(x₀,y₀) fa\` de cercul ( 2 ) este = (x₀-a)² + (y₀-b)² - r²

Cercurile C₁ si C₂ de ecua\ii: x²+ y² + m_Ix + n_iy +p_I=0 , i=1,2 sunt ortogonale m₁m₂+n₁n₂ -

-2(p₁+p₂)=0 .

Ecua\ia cercului care trece prin trei puncte necoliniare date , P_I(x_I,y_I) , I=1,23 este:

x² + y² x y 1

x₁² + y₁² x₁ y₁ 1

x₂² + y₂² x₂ y₂ 1 =0

x₃²+y₃² x₃ y₃ 1

9⁰ Ecua\ia tangentei la cercul ( 1 ) respectiv cercul ( 2 ) in P₀(x₀,y₀) este : xx₀ + yy₀ - r²=0 si

respectiv xx₀ + yy₀ +

10⁰ Ecua\`iile tangentelor la cercurile ( 1 ) si ( 2 ) cu o direc\ie dat` m sunt: y=mxrc@nd

centrul cercului se afl` in origine , respectiv y-b=m(x-a) r c`nd centul este (a,b).

ELIPSA =M/ MF+MF' = 2a, F(c,0), F(-c,0)

1⁰ Elipsa E [n raporta la axe au ecua\ia canonic]` ( 1 ) , a,b lungimile

semiaxelor C= distant`\a de la centru la focare F si F'

B(0,b) y

A'(-a,0) 0 A(a,0)

x

x

B'(0,-b)

2⁰ Elipsa cu centrul O'(p,q) raportat la reperul x0y si av@nd axele paralele cu axele sistemului de

coordonate : ( 2 ) +-1 =0

3⁰ Ecua\iile parametrice ale elipsei sunt x=a cos , y=b sin , [0,2p

4⁰ Ecuatia canonic` a tangentei la elipsa E in P₀(x₀,y₀) E este :

5⁰ Ecua\iile tangente la elips` paralele cu o directie dat` m sunt : y=mx

6⁰ Ecua\ia a tangentelor la E care se pot duce din punctul P₀(x₀,y₀) exterior elipsei este:

(a²-x₀²)(y-y₀)² +2x₀y₀(x- x₀)(y-y₀) + (b²-y₀²)(x-x₀)² =0

7⁰ Locul punctelor de unde se pot duce tangente perpendiculare la elipsa este centrul lui Monge :

x² + y² = a² + b²

8⁰ Ecuat\a normalei la elipsa [n P₀ (x₀, y₀) E este : y - y₀ =(x - x₀ )

9⁰ Excentricitatea elipsei este e=1

10⁰ Aria elipsei este S=p a b

2.3 HIPERBOLA =

y

F'( -c, 0)

0

Hiperbola la axe are ecuatia canonic` ( 1 ) H: , a,b sunt lungimile semiaxelor

c= este distan\a de la centrul 0 la focarele F, F'

2⁰ Hiperbola cu centrul O'( p, q ) raportate la reperul x0y si av@nd axele sale paralele cu axele reperului are ecua\ia ( 2 ) :

3⁰ Ecua\iile parametrice ale hiperbolei sunt : x= ) ; y=), R

4⁰ Ecua\ia hiperbolei conjugate cu ( 1 ) este :

5⁰ Ecuatia hiperbolei este : x² - y² = a²

6⁰ Ecua\ia tangentei la hiperbola H in P₀( x₀, y₀ ) H este

7⁰ Ecua\iile tangentelor la hiperbola paralele cu o directie data m sunt: y=mx

8⁰ Ecua\ia patratica a tangentelor la hiperbola care se pot duce din P₀(x₀ , y₀ ) exterior hiperbolei este:

( a² - x₀² )( y - y₀ )² + 2x₀y₀( x - x₀ ) - ( b²+ y₀² )( x - x₀ )²=0

9⁰ Locul punctelor de unde se pot duce tangente perpendiculare la hiperbola este cercul lui Monge :

x² + y² = a² - b² ,cand a b

10⁰ Ecua\ia normalei la hiperbola [n P₀ (x₀ , y₀) este y -y ₀ = -

11⁰ Raportul distan\elor de la un punct al hiperbolei la focar si la directoarea corespunzatoare este constant ]i egal cu . Acest raport se nume]te excentritate si este supraunitar.

PARABOLA =

y

(D) N M

p - parametrul parabolei

x F - focarul parabolei

0 D - directoarea parabolei

- F(, 0 ) (D): x= -

1⁰ Ecua\ia canonic` a parabolei P raportat la axa ei de simetrie 0x si tangenta la 0y [n v@rful sau 0 este : y² - 2px = 0

2⁰ Parabola cu varful O' ) raportat la reperul x0y ]i av@nd axa si tangenta la v@rf paralele cu axale reperului , este : (y - )² - 2p (x - ) = 0

Ecua\ia x = ay² + by + c reprezint` o paralela cu p = ,

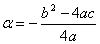
Ecua\iile parametrice ale parabolei sunt : x =

y = R

Ecua\ia tangentei la parabola P in P₀( x₀ , y₀ ) R este yy₀=p( x + x₀)

Ecua\ia tangentei la parabola , paralel` cu o directie data m este : y = mx +

Ecua\ia patratic` a tangentelor la parabola care se pot duce dintr-un punct P₀ (x₀ , y₀) exterior parabolei este : 2x₀( y - y₀ )² - 2y₀(x - x₀)(y - y₀) + p(x - x₀)² = 0

8⁰ Ecua\ia normalei la parabol` [n P₀(x₀ , y₀ ) P este: y - y₀ = -

Excentritatea parabolei este e= 1

PROBLEME :

a) S` se afle centrul ]i raza cercului a c`rei ecuatie este : 3( x² + y² ) - 4x +6y +3 = 0

b) Originea axelor exterioare cercului?

c) S` se scrie ecua\ia tangentei la cerc [n punctul A(0, -1 )

d) S` se scrie ecuat\a tangentei la cerc paralel` cu a doua bisectoare

e) S` se calculeze aria cercului

R: a) Se [mparte ecua\ia la 3 ]i se ob\ine ecuatia normal` , de unde rezult`: a=, b=-1, r²= (C) (x- =0

b) p=3 originea O( 0, 0 ) este exterioar` cercului

c) Deoarece coordonatele punctului A verific` ecua\ia cercului ( C ) ]i se ob\ine ecua\ia : ecua\ia axei y'0y

d) Ecua\ia celei de-a doua bisectoare este y=-x, m =-1 ecua\ia tangentei y+1=( -1 )(x - )

e)A=p r²=

a) S` se determine v@rfurile ]i semiaxele elipsei 2x²+ 4y² - 5 =0

b) S` se scrie ecua\ia tangentei la ( E ) [n punctul C( )

c) S` se scrie ecua\iile tangentelor la ( E ) perpendiculare pe prima bisectoare

d) S` se calculeze aria elipsei

R: a) Ecua\ia se scrie : 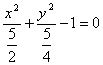din care se deduce : a²=, b²=. V@rfurile sunt

A(), A' (- , B(0,), B'(0,-)

b) Coordonatele punctului C verific` ecua\ia elipsei :ecua\ia tangentei la

( E ) [n C este ecua\ia :

c) x=y , m =1panta tangentelor este m=-1

d) A=pab=

a) S` se determine varfurile , focarele si asinptotele hiperbolei : 2x² -5y² - 8 =0

b) S` se scrie ecuat`\ia tangentei la hiperbol` [n punctul C(2,0)

c) S` se scrie ecua\iile tangentelor la hiperbol` paralele cu dreptele care fac cu axa x'Ox un unghi ( ) =

d) S` se reprezinte hiperbola rapoartelor la ssimptotele de ecuatie : xy=1

R: a) S` se scrie hiperbola sub forma : 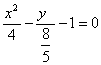( forma gasita prin impar\irea ecua\iei ini\iale la 8 )

a=4 ,b²=V@rfurile sunt A( 2 , 0 ) , A' (-2, 0 ), focarele F ( 2 F' (-2. Ecua\iile asimptotelor se deduc astfel : y=

b) Coordonatele punctului C( 2,0) verific` ecua\ia hiperbolei ecua\ia tangentei la hiperbola [n punctul C este :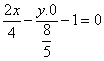

a) Se consider` parabolele fixate respectiv prin :

i)             varful O(0,0) ]i focarul F(2,0)

ii)           focarul F(1,1) ]i directoarea x=2

b)       S` se gaseasc` v@rful , focarul ]i directoarea perabolelor P₁: y²=2x, P₂: x²=- 5y

R: a) i) O( 0 , 0 ) ,F( 2 , 0 )

(D) : x=-2 directoarea

ii) axa de simetrie :y=1; Conform defini\iei : d(M,F) =d(M,D) x²-2x+1+(y-1)² =4x²-4x+4 . Pentru y=1 se ob\ine v@rful V(

parabola intersecteaz` Oy in punctele de ordonate 1 si Oy in (1,0)

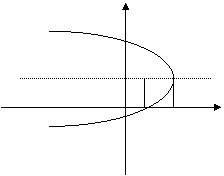
y

(D) y

x=-2 (0,1+)

F V y=1

0 F(2,0) x 0 (0,1-) x

b) P₁: are p=1 , directoarea de ecuaite 2x+1 =0 , focarul F(, varful O(0,0) ]i axa de simetrie Ox

P₂: are p=- focarul F(0,) directoarea y= , v@rful (0,0) axa de simetrie Oy

a) Se da parabola y²=2px. Sa se determine inclinarea tangentei pe care axale de coordonate taie un segment egal cu p

b) Fiind data parabola P:y²=6x ]i punctul M(5,8) s` se gaseasc` normalele parabolei care trec prin M.

R: a) Tangenta y=mx + taie axele [n M()

b) Un punct al parabolei date este N(.Normala [n N are ecua\ia y - a=- . Normala trece prin M a³-12a=114 (a-6)(a² +6x+24)=0 a₁=6R ,a₂,a₃C- R

ecua\a normalei : 2x+y=18

c)       tg=m ecua\ia tangentelor la hiperbol` de directie m sunt :

y=x

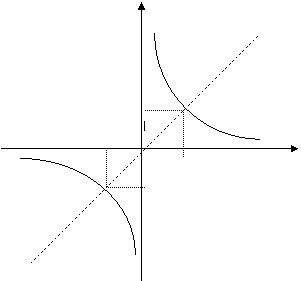d) y

V@rfurile au coordonatele :A₁(1,1), A₂(-1,-1)

Focarele au coordonatele :F₁()

F₁ F₂(-

A₁

Axa trasat` este prima bisectoare y=x

0 45⁰

A₂ x

F₂

Observatie : Pentru a calcula aria f,g sunt exerci\ii [n care trebuie s` reprezentam : cercuri , parabole elipse , hiperbole , s` calcul`m intersec\ia dintre ele pentru a determina limetele de integrare ]i [n final s` calcul`m aria cuprins` [ntre graficele func\iilor f,g ]i dreptele x=a , x=b : Aria (f,g)=

Exemplu: S` se calceluze aria cuprins` [ntre curbele (c₁): x²+y²=8, (c₂): y²=2x

R: Rezolv@nd sistemul x² +y²=2x

Y²=2x

Ob\inem abcisa punctului de intersec\ie dintre cerc ]i parabola x=2

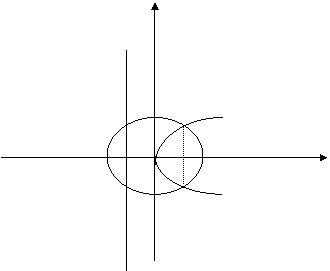
y

(D)

I (2,2)

y= y=

x

0

B(- ,0) B(2,0)

Cercul are centrul [n origine si raza r=2 ,paralela are varful [n origine ,p=1, focarul are coordonate F(,0) si directoarea de ecuatie (D): x= -

Aria cautat` este suma celor doua arii hasurate A(f,g)=A₁+A₂

A₁=2 =

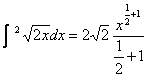
A₂=2 =8 arcsin 1 - 8 arcsin

BACALAUREAT 1998

CLASE CU PROFIL MATAMATIC^ , FIZIC^, INFORMATIC^

VARIANTA 1

(1p) Se consider` punctele A(1,1), B(2,3) ]i dreapta d: x-4y+7=0 . S` se determine coordonatele puctului Cd astfel [ncat ABC s` fie isoscel cu baza (AB) .S` se scrie ecua\ia [nal\imii din C.

VARIANTA 2

(1p) Se consider` cercul de ecua\ie : x<sup>2</sup>+y<sup>2</sup>-6x+3y-5=0 .S` se determine coordonatele centrului ]i raza acestui cerc .S` se scrie ecuat\a tangentei la cerc [n punctul A(-1,-2).S` se precizeze pozit\a punctului

B(0,-4) fa\` de cerc.

VARIANTA 3

(1,5p) Se consider` ABC determinat de dreptele urmatoare : AC): x-3y-4=0, (AB): x+2y-4=0, (BC): 3x+y--2=0. S` se determine coordonatele punctului A. S` se scrie ecua\ia inal\imii din A. S` se afle aria ABC .

VARIANTA 4

(1,25) S` se determine simetricul punctului A(1,2) fat` de dreapta 2x=y+4

VARIASNTA 5

(1p) S` se determine ecua\ia cercului ce trece prin A(-1,5), B(-2,-2) si C(5,5) preciz@nd centrul ]i raza

VARIANTA 6

(1,5) Se consider` A(3,0) , B(0,2) , M(3,-3) ]i N (-2,2). S` se demonstreze c` AN ,BM si perpendiculara din O pe AB sunt concurunte.

CLASE CU PROFIL ECONOMIC

VARIANTA 1

(1,5) S` se afle coordonatele de intersec\ie ale cercului de ecuatie x<sup>2</sup>+y<sup>2</sup>=16 cu parabola de ecua\ie y<sup>2</sup>=6x. Sa se afle aria fiecarei regiuni determinat` de parabol` [n interiorul cercului.

VARIANTA 2

(1p) S` se calculeze aria ABC cu A(0,1), B(4,2),.C(2,3).

VARIANTA 3

(1p) S` se determine centrul ]i raza cercului de ecua\ie : x<sup>2</sup>+y<sup>2</sup>-4x+6y-12=0 ]i s` se scrie ecu\ia tangentei [n punctele cercului care au ordonata nul`.

VARIANTA 4

(1,5) Se consider` f: RR ,f<sub>(x)</sub>=ax<sup>2</sup>+bx<sup>2</sup>+cx+d.S` se precizeze dac` exist` ]i sunt unici coeficien\ii a,b,c,d astfel [nc@t graficul s` treac` prin O(0,0) ,A(1,0), B(-1,-6) iar tangenta la grafic in punctul A s` aib` panta - 5.

(1p) Se consider` A(2,3) , B(- 5,1) , C(1,-3) S` se scrie ecuatia perpendicularei din C pe AB ]i s` se afle coordonatele punctului de intersec\ie dintre AB si perpendiculara dus` din C pe AB.

VARIANTA 5

(1p) S` se determine coordonatale ortocentrului triunghiului format de A(1,4), B(3,- 1), C(8,- 2)

VARIANTA 6

(1p) S` se scrie ecua\ia cecului care trece prin A(1,2), B(2,0) ]i are centrul pe dreapta y=x - 3.

VARIANTA 7

(1p) S` se determine coordonatele punctului de intersec\ie a mediatoarelor segmentelor (AB) ]I (AC) unde A(2,5), C(5,1), C(-2,2)

(1,5p) Se d` hiperbola (H) . S` se afle ecua\ia tangentei la (H) in T(2,3). S` se calculeze aria triunghiului format de asimptotele hiperbolei ]i dreapta :9x-2y-24=0.