ALTE DOCUMENTE
|
|||||||||
GEOMETRIE
 Elemente de geometrie
sintetica plana
Elemente de geometrie
sintetica plana
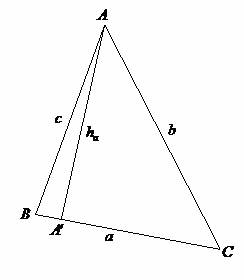
Fie ![]() cu laturile
cu laturile ![]() si
si ![]() înaltimea
din vârful
înaltimea
din vârful ![]() . Avem
urmatoarele:
. Avem
urmatoarele:
Teorema
sinusurilor ![]() , unde
, unde ![]() este raza cercului
circumscris
este raza cercului
circumscris ![]() .
.
Teorema cosinusului ![]()
![]()
![]()
Formule pentru arie ![]()
![]()
Formula lui Heron: ![]() , unde
, unde ![]() (semiperimetrul)
(semiperimetrul)
![]() , unde
, unde ![]() este raza cercului
înscris în
este raza cercului
înscris în ![]() .
.
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() , unde
, unde ![]() este lungimea
bisectoarei unghiului
este lungimea
bisectoarei unghiului ![]() .
.
![]() ,
, ![]() ,
, ![]() , unde
, unde ![]() este lungimea medianei
din
este lungimea medianei
din ![]() .
.
Elemente de geometrie vectoriala
Spunem
ca vectorii legati ![]() si
si ![]() au acelasi sens (sau sunt la fel
orientati) d 454d35e aca au aceeasi directie, iar
extremitatile lor
au acelasi sens (sau sunt la fel
orientati) d 454d35e aca au aceeasi directie, iar
extremitatile lor ![]() se afla în
acelasi semiplan fata de dreapta
se afla în
acelasi semiplan fata de dreapta ![]() , determinata de originile lor (fig. 1). Spunem ca
vectorii legati
, determinata de originile lor (fig. 1). Spunem ca
vectorii legati ![]() si
si ![]() au sensuri opuse (sau sunt orientati
diferit) daca au aceeasi directie, iar extremitatile
lor
au sensuri opuse (sau sunt orientati
diferit) daca au aceeasi directie, iar extremitatile
lor ![]() se afla în
semiplane diferite determinate de dreapata
se afla în
semiplane diferite determinate de dreapata ![]() (fig. 2).
(fig. 2).
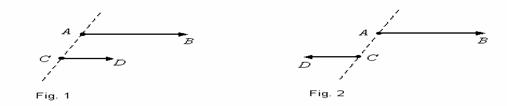
Operatii elementare cu vectori
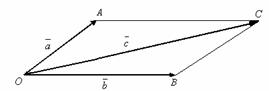
1.Adunarea vectorilor
a) Dupa regula paralelogramului
Fie
vectorii liberi ![]() ,
, ![]() si
si ![]() . Vectorul
. Vectorul ![]() de reprezentant
de reprezentant ![]() (care porneste
din originea comuna) reprezinta prin definitie suma vectorilor
(care porneste
din originea comuna) reprezinta prin definitie suma vectorilor ![]() ,
, ![]() si scriem
si scriem ![]() .
.
b) Dupa regula triunghiului
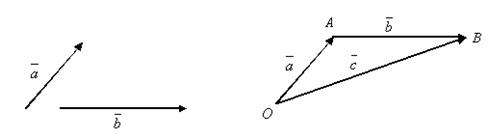
Fie
ca mai sus vectorii liberi ![]() ,
, ![]() . Consideram
. Consideram ![]() , reprezentanti ai vectorilor
, reprezentanti ai vectorilor ![]() si respectiv
si respectiv ![]() . Atunci vectorul suma a vectorilor
. Atunci vectorul suma a vectorilor ![]() ,
, ![]() este vectorul
este vectorul ![]() de reprezentant
de reprezentant ![]() .
.
Observatie. Pentru adunarea a trei sau mai multi vectori se plica succesiv regula triunghiului sau regula poligonului.
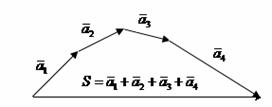
2.Scaderea vectorilor
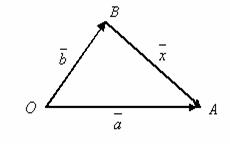 Fie
Fie ![]() doi vectori. Atunci
diferenta lor este vectorul
doi vectori. Atunci
diferenta lor este vectorul ![]() definit prin
definit prin ![]() . Vectorul diferenta
. Vectorul diferenta ![]() se construieste
unind extremitatea vectorului scazator cu extremitatea vectorului
descazut.
se construieste
unind extremitatea vectorului scazator cu extremitatea vectorului
descazut.
![]()
3.Înmultirea unui vector cu un scalar
Definitie. Fie ![]() un numar real
si
un numar real
si ![]() un vector. Produsul
dintre numarul real
un vector. Produsul
dintre numarul real ![]() si vectorul liber
si vectorul liber
![]() este vectorul notat
este vectorul notat ![]() având :
având :
aceeasi directie cu ![]() ;
;
acelasi sens cu ![]() daca
daca ![]() ; sens contrar lui
; sens contrar lui ![]() daca
daca ![]() ;
;
modulul egal cu produsul dintre ![]() si modulul
vectorului
si modulul
vectorului ![]() , adica
, adica ![]() .
.
Observatie. Doi vectori liberi nenuli se numesc coliniari daca au aceeasi directie. În caz contrar vectorii se numesc necoliniari.
Doi
vectori nenuli ![]() ,
, ![]() sunt coliniari daca si numai
daca exista
sunt coliniari daca si numai
daca exista ![]() astfel încât
astfel încât ![]() .
.
Se
numeste vector director al unei
drepte ![]() , orice vector liber nenul
, orice vector liber nenul ![]() , având directia dreptei
, având directia dreptei ![]() . Daca vectorul
. Daca vectorul ![]() are lungimea
egala cu unu, atunci acesta se numeste versor director.
are lungimea
egala cu unu, atunci acesta se numeste versor director.
 Vectorii necoliniari
nenuli
Vectorii necoliniari
nenuli ![]() ,
, ![]() ale caror
directii sunt paralele cu planul P se numesc vectorii directori ai planului P . (În acest caz orice vector
ale caror
directii sunt paralele cu planul P se numesc vectorii directori ai planului P . (În acest caz orice vector ![]() al planului P se scrie ca o
combinatie liniara de vectorii directori,
al planului P se scrie ca o
combinatie liniara de vectorii directori, ![]() , cu
, cu ![]() .
.
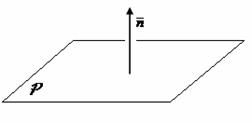
Un
vector nenul ![]() se numeste vector normal la planul P daca un
reprezentant al sau are dreapta suport perpendiculara pe planul P
se numeste vector normal la planul P daca un
reprezentant al sau are dreapta suport perpendiculara pe planul P
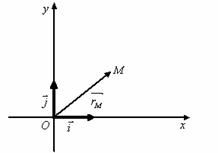 Fie în planul P reperul
Fie în planul P reperul ![]() , iar
, iar ![]() P . Atunci vectorul
P . Atunci vectorul ![]() îl numim vector legat
(de punctul
îl numim vector legat
(de punctul ![]() ) sau vector de pozitie. (Vectorul
) sau vector de pozitie. (Vectorul ![]() îl notam
îl notam ![]() ).
).
Mai
mult daca ![]() , atunci
, atunci ![]() , adica coordonatele punctului
, adica coordonatele punctului ![]() sunt coordonatele
vectorului de pozitie
sunt coordonatele
vectorului de pozitie ![]() , adica
, adica ![]() .
.
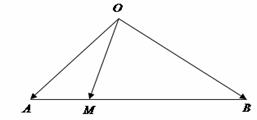 Teorema. Fie
Teorema. Fie ![]() un punct pe segmentul
un punct pe segmentul ![]() astfel încât
astfel încât ![]() , atunci pentru orice punct
, atunci pentru orice punct ![]() din plan are loc
relatia:
din plan are loc
relatia:
![]() .
.
Operatii cu vectori legati
Fie
![]() ,
, ![]() doi vectori
legati. Atunci
doi vectori
legati. Atunci 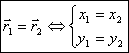 .
.
Adunarea. Suma a doi vectori legati ![]() ,
, ![]() este vectorul notat
este vectorul notat ![]() având coordonatele
având coordonatele ![]() .
.
Înmultirea unui vector cu un
scalar.
Înmultirea vectorului legat ![]() cu scalarul
cu scalarul ![]() este vectorul notat
este vectorul notat ![]() având coordonatele
având coordonatele ![]() .
.
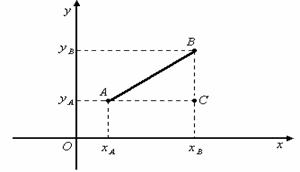
Modulul vectorului ![]() este egal cu :
este egal cu :
![]()
Doi vectori ![]() ,
, ![]() sunt coliniari
daca au coordonatele proportionale :
sunt coliniari
daca au coordonatele proportionale : ![]() .
.
Coordonatele punctului ![]() care împarte segmentul
care împarte segmentul
![]() în raportul
în raportul ![]() ,
, ![]() ,
, ![]() sunt :
sunt : 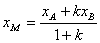 ,
, ![]() . În particular,
daca
. În particular,
daca ![]() este mijlocul
segmentului
este mijlocul
segmentului ![]() , atunci
, atunci ![]()
![]() ,
, ![]() .
.
Produsul scalar a doi vectori
Fie
în plan sau în spatiu o axa ![]() cu versorul
cu versorul ![]() si un vector
arbitrar
si un vector
arbitrar ![]() . Proiectia
ortogonala (sau simpu proiectia) vectorului
. Proiectia
ortogonala (sau simpu proiectia) vectorului ![]() pe axa
pe axa ![]() este un numar
egal cu produsul lungimii lungimii vectorului
este un numar
egal cu produsul lungimii lungimii vectorului ![]() cu cosinusul unghiului
dintre vectorii
cu cosinusul unghiului
dintre vectorii ![]() si
si ![]() .
.

Produsul scalar al vectorilor ![]() ,
, ![]() este numarul
notat
este numarul
notat ![]() , unde
, unde ![]() este unghiul
facut de vectorii
este unghiul
facut de vectorii ![]() si
si ![]() .
.
Proprietati
Doi vectori nenuli sunt perpendiculari daca si numai daca produsul lor scalar este egal cu 0.
Produsul scalar a doi vectori de acelasi sens este egal cu produsul modulelor lor.
![]()
Produsul scalar în plan
Fie ![]() ,
, ![]() doi vectori în plan.
Atunci
doi vectori în plan.
Atunci ![]() .
.
Modulul unui vector : Fie ![]() . Atunci
. Atunci ![]() .
.
Calculul unghiului a doi vectori : Fie ![]() ,
, ![]() doi vectori nenuli în
plan, iar
doi vectori nenuli în
plan, iar ![]() unghiul dintre ei.
Atunci :
unghiul dintre ei.
Atunci : 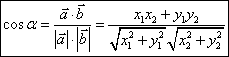 .
.
Vectorii ![]() ,
, ![]() sunt perpendiculari
daca si numai daca
sunt perpendiculari
daca si numai daca ![]() .
.
Produsul scalar în spatiu
Fie ![]() ,
, ![]() doi vectori în
spatiu. Atunci
doi vectori în
spatiu. Atunci ![]() .
.
Modulul unui vector : ![]() .
.
Cosinusul unghiului a doi vectori : 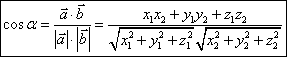 .
.
Elemente de geometrie analitica plana
Fie
![]() o dreapta oblica din plan. Numarul real
o dreapta oblica din plan. Numarul real ![]() , unde
, unde ![]() este unghiul
facut de dreapta cu sensul pozitiv al axei
este unghiul
facut de dreapta cu sensul pozitiv al axei ![]() , se numeste panta
dreptei
, se numeste panta
dreptei ![]() .
.
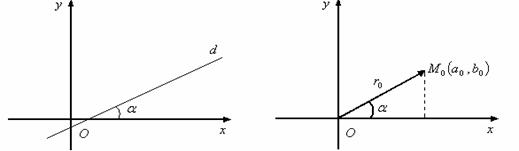
Panta unei directii determinate de vectorul ![]() ,
, ![]() este egala cu
este egala cu ![]() .
.
Consideram punctele distincte ![]() ,
, ![]() cu
cu ![]() . Panta dreptei ce trece prin punctele
. Panta dreptei ce trece prin punctele ![]() este :
este : ![]() .
.
Doua drepte oblice sunt paralele daca si numai daca au pantele egale si sunt perpendiculare daca si numai daca produsul pantelor lor este egal cu -1.
Forme ale ecuatiei dreptei în plan
Consideram punctul ![]() si vectorul
si vectorul ![]() . Ecuatiile
. Ecuatiile 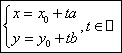 se numesc ecuatiile parametrice ale dreptei
se numesc ecuatiile parametrice ale dreptei ![]() .
.
Ecuatia dreptei ce trece prin punctul ![]() si are panta
si are panta ![]() este :
este : ![]() .
.
Ecuatia dreptei determinata de doua puncte distincte ![]() ,
, ![]() ,
, ![]() este:
este: 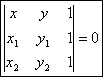 . Daca
. Daca ![]() , atunci ecuatia dreptei este
, atunci ecuatia dreptei este ![]() .
.
Daca punctele ![]() sunt situate pe axele
de coordonate adica daca
sunt situate pe axele
de coordonate adica daca ![]() ,
, ![]() , cu
, cu ![]() atunci ecuatia
dreptei are forma
atunci ecuatia
dreptei are forma ![]() , numita ecuatia dreptei prin taieturi.
, numita ecuatia dreptei prin taieturi.
Ecuatia carteziana generala a unei drepte : ![]() . Panta dreptei date în forma generala este
. Panta dreptei date în forma generala este ![]() , daca
, daca ![]() . Daca
. Daca ![]() , atunci dreapta este verticala, deci nu are panta.
, atunci dreapta este verticala, deci nu are panta.
Observatii. Punctul ![]() apartine dreptei
(se afla pe dreapta)
apartine dreptei
(se afla pe dreapta) ![]() , daca coordonatele sale verifica ecuatia
dreptei, adica daca
, daca coordonatele sale verifica ecuatia
dreptei, adica daca ![]() .
.
Conditia de coliniaritate a trei puncte ![]() ,
, ![]() ,
, ![]() este
este 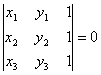 .
.
Punctul de intersectie a doua drepte se obtine rezolvând sistemul format din ecuatiile dreptelor.
Doua drepte ![]() ,
, ![]() coincid daca
si numai daca au coeficientii proportionali, adca :
coincid daca
si numai daca au coeficientii proportionali, adca : ![]() .
.
Conditia de concurenta
a trei drepte ![]() , unde
, unde ![]() si
si ![]() ,
, ![]() .
.
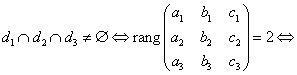
 si exista un
minor de ordinul 2 nenul.
si exista un
minor de ordinul 2 nenul.
 Unghiul a doua drepte
Unghiul a doua drepte
Fie
dreptele ![]() ,
, ![]() , niciuna paralela cu axa
, niciuna paralela cu axa ![]() . Avem :
. Avem :
![]() ,
, ![]() si
si ![]() , atunci:
, atunci:
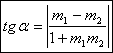 .
.
Distanta de la un punct la o dreapta
Distanta
de la punctul ![]() la dreapta
la dreapta ![]() de ecuatie
de ecuatie ![]() este data de
formula
este data de
formula
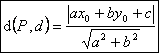 .
.
Aria unui triunghi
Fie
![]() ,
, ![]() ,
, ![]() vârfurile triunghiului
vârfurile triunghiului
![]() . Aria triunghiului
. Aria triunghiului ![]() este data de
formula
este data de
formula ![]() , unde
, unde 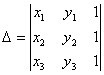 .
.
Coordonatele centrului de
greutate
![]() al unui triunghi cu
vârfurile
al unui triunghi cu
vârfurile ![]() , unde
, unde ![]() sunt
sunt
![]() ,
, ![]() .
.
Elemente de geometrie analitica în spatiu
Distanta
dintre doua puncte ![]() si
si ![]() este
este ![]() .
.
Ecuatii ale planului în spatiu
Fie
vectorul ![]() . Numerele
. Numerele ![]() se numesc parametrii
directori ai directiei dreptei
se numesc parametrii
directori ai directiei dreptei ![]() (sau simplu parametrii
directori ai dreptei
(sau simplu parametrii
directori ai dreptei ![]() ).
).
Ecuatia vectoriala a planului care trece prin ![]() si care este
perpendicular pe
si care este
perpendicular pe ![]() este :
este : ![]() unde
unde ![]() este vectorul de
pozitie al unui punct curent al planului,
este vectorul de
pozitie al unui punct curent al planului, ![]() este vectorul de
pozitie al punctului
este vectorul de
pozitie al punctului ![]() .
.
Ecuatia planului determinat de trei puncte necoliniare ![]() este:
este:
 .
.
Conditia ca de trei puncte ![]() sa fie coliniare
este:
sa fie coliniare
este: 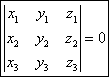 .
.
Conditia ca patru puncte ![]() sa fie coplanare
este:
sa fie coplanare
este:
 .
.
Ecuatia generala a planului : ![]() , unde
, unde ![]() si
si ![]() .
.
Observatie. Vectorul ![]() este perpendicular pe
planul de ecuatie
este perpendicular pe
planul de ecuatie ![]() si se
numeste normal la plan.
si se
numeste normal la plan.
Ecuatia normala a planului ce trece prin ![]() este:
este: ![]() .
.
Ecuatia unui plan care trece prin origine este: ![]() , unde
, unde ![]() si
si ![]() .
.
Planul paralel cu axa ![]() are ecuatia :
are ecuatia : ![]() , unde
, unde ![]() si
si ![]() .
.
Planul paralel cu axa ![]() are ecuatia :
are ecuatia : ![]() , unde
, unde ![]() si
si ![]() .
.
Planul paralel cu axa ![]() are ecuatia :
are ecuatia : ![]() , unde
, unde ![]() si
si ![]() .
.
Planul paralel cu ![]() are ecuatia :
are ecuatia : ![]() , etc, unde
, etc, unde ![]() si
si ![]() .
.
Planele ![]() si
si ![]() sunt :
sunt :
Forme ale ecuatiei dreptei în spatiu
Ecuatiile
parametrice ale dreptei ce trece prin ![]() si are vectorul
director
si are vectorul
director ![]() :
:
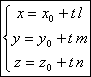 ,
, ![]() .
.
Ecuatiile dreptei trece prin ![]() si are vectorul
director
si are vectorul
director ![]() în forma
canonica:
în forma
canonica:
![]() .
.
Ecuatia vectoriala a dreptei determinata de
doua puncte : ![]() .
.
Ecuatiile parametrice ale dreptei determinate de
doua puncte ![]() si
si ![]() :
:
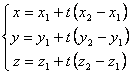 ,
, ![]() .
.
Ecuatiile canonice ale dreptei determinate de doua
puncte ![]() si
si ![]() :
:
![]() ,
, ![]() .
.
Ecuatia dreptei ca intersectie a doua plane ![]() si
si ![]() :
:
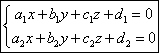 , daca
, daca 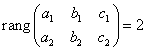 .
.
Exemplu: Daca 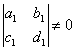 , atunci obtinem
, atunci obtinem 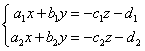 , notam
, notam ![]() ,
, ![]() si avem
si avem
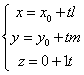 ,
, ![]() (adica
ecuatiile parametrice ale dreptei).
(adica
ecuatiile parametrice ale dreptei).
Pozitiile a doua drepte
în spatiu Fie 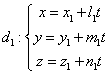 si
si  doua drepte cu
vectorii directori
doua drepte cu
vectorii directori ![]() si respectiv
si respectiv ![]() , atunci:
, atunci:
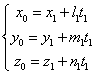 si respectiv
si respectiv
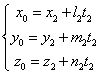 si
rezolvam sistemul
si
rezolvam sistemul 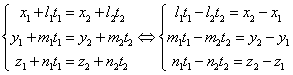 .
.Unghiul ![]() dintre doua
drepte
dintre doua
drepte ![]() si
si ![]() este dat de formula:
este dat de formula: 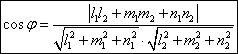 (se formeaza
doua unghiuri, îl alegem pe cel ascutit).
(se formeaza
doua unghiuri, îl alegem pe cel ascutit).
Pozitia unei drepte
fata de un plan Fie dreapta ![]() si planul
si planul ![]() , atunci:
, atunci:
Observatie. Pentru a determina
punctul de intersectie dintre dreapta si plan în cazul a).
Scriem ecuatia dreptei sub forma parametrica si înlocuim în
ecuatia planului, de unde se determina parametrul ![]() , cu acesta ne întoarcem la ecuatiile parametrice ale
dreptei si gasim coordonatele punctului de intersectie.
, cu acesta ne întoarcem la ecuatiile parametrice ale
dreptei si gasim coordonatele punctului de intersectie.
Unghiul format de o dreapta
cu un plan Fie dreapta ![]() , planul
, planul ![]() si
si ![]() unghiul format de
dreapta
unghiul format de
dreapta ![]() cu planul
cu planul ![]() , atunci:
, atunci:
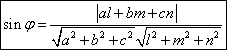 .
.
Unghiul dintre doua plane Fie ![]() ,
, ![]() doua plane
si
doua plane
si ![]() unghiul format de cele
doua plane, atunci
unghiul format de cele
doua plane, atunci 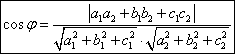
Distanta de la un punct ![]() la planul
la planul ![]() este data de
formula:
este data de
formula:
 .
.
Aria triunghiului cu vârfurile ![]() ,
, ![]() este dat de formula:
este dat de formula: ![]() , unde
, unde 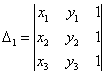 ,
, 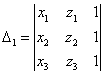 ,
, 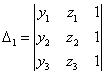 .
.
Coordonatele centrului de
greutate ![]() al unui triunghi cu
vârfurile
al unui triunghi cu
vârfurile ![]() ,
, ![]() sunt:
sunt:
![]() .
.
Volumul unui tetraedru cu vârfurile ![]() ,
, ![]() este dat de formula :
este dat de formula : ![]() , unde
, unde
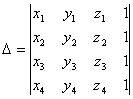 .
.
Curbe Plane
1. Cercul
![]() Definitie. Cercul
Definitie. Cercul ![]() de centru
de centru ![]() si raza
si raza ![]() este multimea punctelor
este multimea punctelor
![]() din plan cu
propriettea ca
din plan cu
propriettea ca ![]() (fig. 2).
(fig. 2).
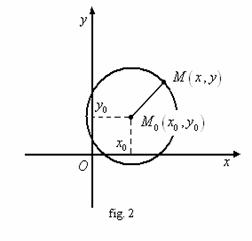
![]() Ecuatii ale cercului
Ecuatii ale cercului
1. Ecuatia implicita
![]()
2. Ecuatiile parametrice
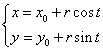 ,
, ![]() parametru.
parametru.
3. Ecuatiile explicite
![]() (ecuatia semicercului superior)
(ecuatia semicercului superior)
![]() (ecuatia
semicercului inferior).
(ecuatia
semicercului inferior).
![]() Daca notam
Daca notam ![]() ,
, ![]() , atunci:
, atunci:
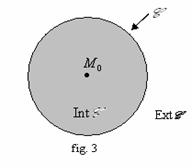
Interiorul cercului: ![]()
Cercul: ![]()
Exteriorul cercului: ![]() .
.
(vezi fig. 3)
![]() 1. Ecuatia
tangentei la cercul
1. Ecuatia
tangentei la cercul ![]() în punctul
în punctul ![]() :
:
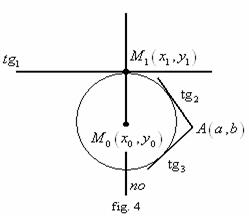
![]() . (vezi fig. 4).
. (vezi fig. 4).
2. Ecuatiile tangentelor de directie data ![]() la cercul
la cercul ![]() :
:
![]()
Se pune apoi conditia ca ![]() sa
apartina tangentei si se determina
sa
apartina tangentei si se determina ![]() :
:
![]() . (vezi fig. 4).
. (vezi fig. 4).
![]() Ecuatia normalei la cercul
Ecuatia normalei la cercul ![]() în punctul
în punctul ![]() :
:
![]() . (vezi fig. 4).
. (vezi fig. 4).
2. Elipsa
![]() Definitie.
Fie
Definitie.
Fie ![]() ,
, ![]() si
si ![]() doua puncte
fixate din plan astfel încât
doua puncte
fixate din plan astfel încât ![]() . Fie
. Fie ![]() . Multimea
. Multimea ![]() a punctelor
a punctelor ![]() cu proprietatea
ca
cu proprietatea
ca ![]() se numeste elipsa. (vezi fig. 5).
se numeste elipsa. (vezi fig. 5).
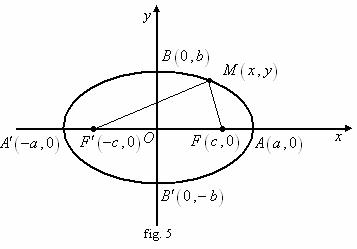 Elementele elipsei
Elementele elipsei
1). ![]() si
si ![]() se numesc focarele
elipsei;
se numesc focarele
elipsei;
2). ![]() se numeste axa
focala;
se numeste axa
focala;
3). ![]() distanta
focala;
distanta
focala;
4). ![]() si
si ![]() se numesc razele
focale ale punctului M;
se numesc razele
focale ale punctului M;
5). ![]() (mediatoarea segmentului
(mediatoarea segmentului ![]() ) si
) si ![]() se numesc axe de
simetrie;
se numesc axe de
simetrie;
6). ![]() se numeste centru
de simetrie.
se numeste centru
de simetrie.
7). ![]() ,
, ![]() ,
, ![]() ,
, ![]() se numesc vârfurile
elipsei;
se numesc vârfurile
elipsei;
8). ![]() se numeste axa
mare iar
se numeste axa
mare iar ![]() se numeste axa
mica;
se numeste axa
mica;
 9).
9). ![]() se numesc semiaxe.
se numesc semiaxe.
![]() Ecuatiile elipsei:
Ecuatiile elipsei:
Ecuatia implicita ![]() , unde
, unde ![]() .
.
2). Ecuatiile parametrice: ![]() ,
, ![]() (parametru)
(parametru)
3). Ecuatiile explicite:  , unde
, unde ![]() corespunde
portiunii din
corespunde
portiunii din ![]() din semiplanul
superior, iar
din semiplanul
superior, iar ![]() corespunde
portiunii din
corespunde
portiunii din ![]() din semiplanul
inferior.
din semiplanul
inferior.
![]() Daca notam
Daca notam ![]() ,
, ![]() , atunci:
, atunci:
Interiorul elipsei: ![]()
Elipsa: ![]()
Exteriorul elipsei: ![]() (vezi fig. 6).
(vezi fig. 6).
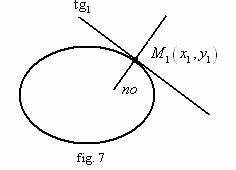
![]() 1. Ecuatia tangentei la elipsa
într-un punct dat
1. Ecuatia tangentei la elipsa
într-un punct dat ![]() :
:
![]() (vezi fig. 7)
(vezi fig. 7)
2. Ecutia tangentelor de directie data ![]() la
la ![]() :
:
![]() .
.
Se pune conditia ca ![]() si se
determina
si se
determina ![]() .
. ![]() .
.
![]() Ecuatia normalei la elipsa
Ecuatia normalei la elipsa ![]() în punctul
în punctul ![]() :
:
![]() (vezi fig. 7).
(vezi fig. 7).
 3. Hiperbola
3. Hiperbola
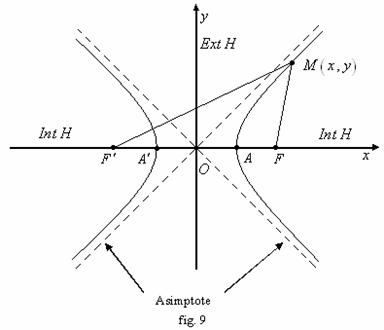
![]() Definitie.
Fie
Definitie.
Fie ![]() si
si ![]() si
si ![]() doua puncte
fixate din plan astfel încât
doua puncte
fixate din plan astfel încât ![]() . Fie
. Fie ![]() . Multimea
. Multimea ![]() punctelor
punctelor ![]() cu proprietatea
cu proprietatea ![]() se numeste hiperbola. (vezi fig. 9).
se numeste hiperbola. (vezi fig. 9).
Elementele hiperbolei
1). ![]() si
si ![]() se numesc focarele
hiperbolei;
se numesc focarele
hiperbolei;
2). ![]() se numeste axa
focala;
se numeste axa
focala;
3). ![]() distanta
focala;
distanta
focala;
4). ![]() si
si ![]() se numesc razele
focale ale punctului M;
se numesc razele
focale ale punctului M;
5). ![]() si mediatoarea
segmentului
si mediatoarea
segmentului ![]() se numesc axe de
simetrie;
se numesc axe de
simetrie;
6). Punctele ![]() ,
, ![]() se numesc vârfurile
hiperbolei;
se numesc vârfurile
hiperbolei;
7). ![]() - axa transversala,
- axa transversala, ![]() - axa netransversala.
- axa netransversala.
![]() Ecuatiile hiperbolei:
Ecuatiile hiperbolei:
Ecuatia implicita ![]() , unde
, unde ![]() .
.
2). Ecuatiile parmetrice:
Ramura ![]() :
: ![]() , cu
, cu ![]() are ecuatiile
parametrice:
are ecuatiile
parametrice: ![]() ,
, ![]() .
.
Ramura ![]() , cu
, cu ![]() are ecuatiile
parametrice:
are ecuatiile
parametrice: ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() .
.
 3). Ecuatiile explicite:
3). Ecuatiile explicite:  ,
, ![]() . (
. (![]() portiunea de
portiunea de ![]() din semiplanul
din semiplanul ![]() ,
, ![]() portiune de H din
semiplanul
portiune de H din
semiplanul ![]() ).
).
![]() Daca notam
Daca notam ![]() ,
, ![]() , atunci:
, atunci:
Interiorul hiperbolei: ![]()
Hiperbola: ![]()
Exteriorul hiperbolei: ![]() .
.
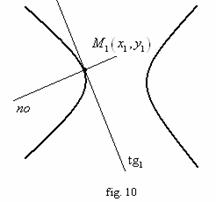
![]() 1. Ecuatia tangentei la
hiperbola într-un punct dat
1. Ecuatia tangentei la
hiperbola într-un punct dat ![]() :
:
![]() (vezi fig. 10)
(vezi fig. 10)
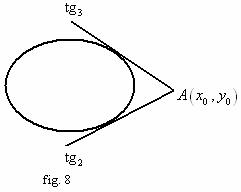
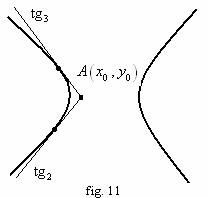
2. Ecuatia
tangentelor de directie ![]() data la
data la ![]() :
:
![]() . (vezi fig. 11)
. (vezi fig. 11)
se
pune conditia ca ![]() si se
determina
si se
determina ![]() .
.
![]() .
.
![]() Ecuatia normalei la hiperbola
Ecuatia normalei la hiperbola ![]() în punctul
în punctul ![]() :
: ![]() (vezi fig. 10).
(vezi fig. 10).
![]() Asimptotele hiperbolei:
Asimptotele hiperbolei: ![]() si
si ![]() .
.
4. Parabola

![]() Definitie.
Fie
Definitie.
Fie ![]() o dreapta din
plan si
o dreapta din
plan si ![]() un punct exterior
dreptei. Multimea
un punct exterior
dreptei. Multimea ![]() a punctelor
a punctelor ![]() cu proprietatea
cu proprietatea ![]() se numeste parabola. (vezi fig. 12)
se numeste parabola. (vezi fig. 12)
Elementele parabolei:
1). ![]() se numeste
focarul parabolei;
se numeste
focarul parabolei;
2). ![]() se numeste
directoarea parabolei;
se numeste
directoarea parabolei;
3). ![]() se numeste raza
focala a punctului
se numeste raza
focala a punctului ![]() ;
;
4). ![]() ,
, ![]() axa de simetrie a
parabolei;
axa de simetrie a
parabolei;
5). ![]() ,
, ![]() parametrul parabolei;
parametrul parabolei;
6). ![]() vârful parabolei;
vârful parabolei;
7). ![]() - axa transversala,
- axa transversala, ![]() - axa netransversala.
- axa netransversala.
![]() Ecuatiile parabolei:
Ecuatiile parabolei:
Ecuatia implicita ![]() .
.
2). Ecuatiile parametrice: 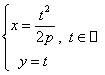 parametru.
parametru.
3). Ecuatiile explicite: 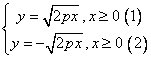
![]() portiunea de
portiunea de ![]() din cadranul I
din cadranul I ![]() ,
, ![]() portiunea de
portiunea de ![]() din cadranul IV
din cadranul IV ![]() .
.
![]() Daca notam
Daca notam ![]() ,
, ![]() , atunci:
, atunci:
 Interiorul parabolei:
Interiorul parabolei: ![]()
Parabola: ![]()
Exteriorul parabolei: ![]()
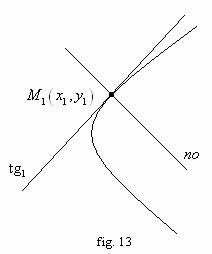
![]() 1. Ecuatia tangentei la parabola
într-un punct dat
1. Ecuatia tangentei la parabola
într-un punct dat ![]() :
: ![]() (vezi fig. 13)
(vezi fig. 13)
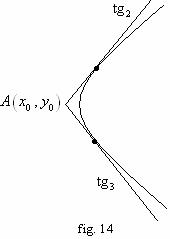
2. Ecutiile tangentelor de directie data ![]() la
la ![]() :
: ![]() . (vezi fig. 14)
. (vezi fig. 14)
Se pune conditia ca punctul ![]() sa se afle pe
parabola si se determina
sa se afle pe
parabola si se determina ![]() .
.
![]() .
.
![]() Ecuatia normalei la parbola
Ecuatia normalei la parbola ![]() în punctul
în punctul ![]() :
: ![]() .
.
|