Grade de libertate
Notiunea de grad de libertate este oarecum similara celei din problemele de mecanica.
Anume, daca un punct se afla pe o axa, se spune despre el ca are un grad de libertate, pentru ca nu putem sa modificam la un moment dat decāt distanta lui pāna la origine. D 24124g620y aca īnsa punctul se afla īntr-un plan atunci el are doua grade de libertate, caci se pot modifica independent unul de altul, adica liber, doua marimi, abscisa lui si ordonata. Daca se afla īn spatiu, are trei grade de libertate conform celor trei dimensiuni care exprima pozitia lui si care se pot modofica liber.
Daca un punct se misca pe o axa, atunci i se asociaza uneori trei grade de libertate deoarece miscarea este descrisa complet daca stim pozitia lui, viteza si acceleratia. Deci el este caracterizat la un moment dat de trei numere.
Un punct care se misca īn spatiu, este uneori modelat ca avānd noua grade de libertate, trei pentru pozitie, trei pentru viteza si trei pentru acceleratie.
Daca punctul este supus la anumite legaturi care īl obliga sa se miste numai īntr-un anumit fel, are mai putine grade de libertate. De exemplu, daca obligam un punct sa se miste īn spatiu, dar pe o sfera, nu mai are noua grade de libertate ci numai sase.
Īntr-un fenomen mai complex decāt miscarea unui punct putem avea mult mai multe grade de libertate. De exemplu, daca doua puncte se afla pe o axa, sistemul format din cele doua puncte are doua grade de libertate. Daca sunt 100 de puncte, avem 100 de grade de libertate, deoarece avem posibilitatea de a alege locul celor 100 de puncte independent unul de altul, oriunde pa axa.
Īn general, daca alegem n numere reale, sau le obtinem printr-o operatie de masurare, avem n grade de libertate, deoarece este ca si cānd am fixa n puncte, īn mod liber pe o dreapta.
Īn statistica, se considera ca daca se iau īn calcul n valori independente una de alta, avem n grade de libertate. Deoarece īn general īn studiile statistice, indivizii pe care se fac masuratorile sunt alesi aleator si se masoara parametri cum ar fi hemoglobina sau calcemia sau glicemia, etc, nu avem nici un motiv sa credem ca valorile obtinute nu sunt independente. E ca si cum am pretinde ca valoarea obtinuta pentru glicemia pacientului x are o strānsa legatura cu valoarea pentru pacientul y, ceea ce este absurd.
Mai pe scurt, īn masuratorile dedicate studiului statistic, de obicei avem relatia:
La n pacienti pe care s-au facut masuratori avem n masuratori independente si deci n grade de libertate
De exemplu, atunci cānd calculam media de esantionare pentru un esantion de n indivizi, aven n grade de libertate.
Daca totul ar fi asa de simplu, nu ar mai avea rost toata discutia despre gradele de libertate. Dar nu totdeauna n indivizi īntr-un esantion īnseamna n grade de libertate. De exemplu, daca dorim sa calculam dispersia de esantionare pe un esantion de n indivizi, avem n-1 grade de libertate. Aceasta deoarece īn calculul dispersiei intervine si media de esantionare care se comporta ca o legatura si reduce cu 1 numarul de grade de libertate. Aceasta reducere care se datoreaza faptului ca ne este cunoscuta media de esantionare, si are o asemanare cu un fapt banal, care, īn parte o si explica.
Daca un elev are notele 8, 8, 9, 10, 10, va avea media 9. Dar daca are notele 8, 8, 9, 10 si se īntraba ce nota trebuie sa ia, astfel ca media sa fie exact 9, va ajunge la concluzia ca ultima nota trebuie sa fie 10. Asadar, aceasta ultima nota nu este oarecare, ea depinde de celelalte si de medie. Asa se petrec lucrurile si cānd calculam dispersia. Una din valori nu este independenta, depinde de celelalte si de medie. Doar n-1 din valori sunt independente, deci avem n-1 grade de libertate.
La fel, īn capitolul teste statistice se va calcula statistica:
,
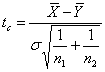unde 
si 
reprezinta mediile a doua serii de valori, una
avānd n1 valori, iar
cealalta n2 valori.
Īn calculul acestei variabile aleatoare (sau statistici), avem n1+n2 valori, dar
independente sunt numai n1+n2-2
deoarece cunoasterea celor doua medii, reduce cu 2 numarul de
valori independente. Deci, avem n1+n2-2
grade de libertate.
|
