INDICATORII ASIMETRIEI

INDICATORII ASIMETRIEI

Reprezentarea grafica a seriilor cu distributie de frecventa

Tipuri de asimetrie

Coeficientul de asimetrie

6.1. Reprezentarea grafica a seriilor cu distributie de frecventa

Seria cu distributie de frecvente este rezultatul gruparii colectivitatii, în functie de variantele sau intervalele de variatie ale unei caracteristici.

De exemplu, pentru cei 20 de angajati ai unei firme s-au înregistrat, în luna septembrie 2006, urmatoarele câ 919b17j stiguri salariale nete (sunt prezentate trei variante diferite din punct de vedere al distributiei angajatilor pe grupe de salarii).

Tabelul 6.1

Distributia salariatilor pe grupe de salarii nete

Sursa: Evidentele primare ale firmei.

Nota: Limita inferioara este inclusa în interval.

O prima imagine asupra formei repartitiei se obtine prin intermediul reprezentarilor grafice ale seriilor cu distributie de frecvente, care se vizualizeaza - de regula - prin doua tipuri de grafice, construite pe acelasi sistem de axe:

A. Histograma se construieste astfel:

- pe axa abciselor (O_x) se trec valorile variabilei care delimiteaza grupele/clasele, în cazul nostru salariile nete (X_i);

- pe axa ordonatelor (O_y) se trec valorile frecventelor de grupa (f_i), în cazul nostru numarul salariatilor;

- se construiesc dreptunghiuri de înaltimi egale cu frecventele de repartitie si cu baze egale cu marimea intervalului/variantei de grupare.

B. Poligonul frecventelor se reprezinta astfel:

- se construieste prin unirea succesiva, prin segmente de dreapta, a mijloacelor bazelor superioare ale dreptunghiurilor.

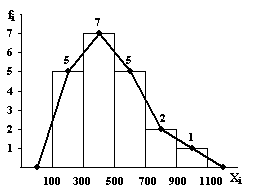
Fig. 6.1: Varianta A

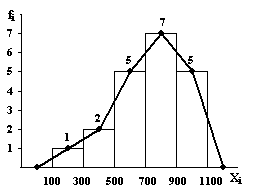
Fig. 6.2: Varianta B

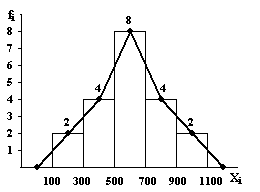
Fig. 6.3: Varianta C

6.2. Tipuri de asimetrie

Orice serie statistica simpla, cu un numar suficient de mare de termeni, se poate transforma, prin gruparea acestora, într-o serie cu distributie de frecvente.

O serie cu distributie de frecvente poate sa fie:

- simetrica, daca valorile variabilei sunt egal dispersate de o parte si de alta a valorii centrale.

în cazul în care repartitia este perfect simetrica (numita repartitie normala), între indicatorii tendintei centrale exista o relatie de egalitate:

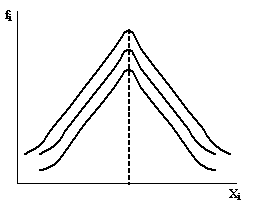
Fig. 6.4: Distributia simetrica a frecventelor de aparitie

- asimetrica, daca valorile variabilei sunt inegal dispersate de o parte si de alta a valorii centrale.

Asimetria poate fi:

asimetrie spre stânga (sau pozitiva), când valorile caracteristicii, mai mici decât nivelul mediu, au frecvente foarte mari si ca urmare:

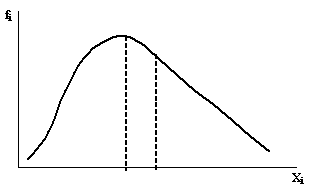
Fig. 6.5: Distributia asimetrica spre stânga a frecventelor de aparitie

asimetrie spre dreapta (sau negativa), când valorile caracteristicii, mai mari decât nivelul mediu, au frecvente foarte mari si ca urmare:

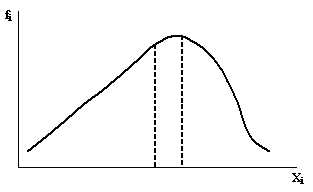
Fig. 6.6: Distributia asimetrica spre dreapta a frecventelor de aparitie

6.3 Coeficientul de asimetrie

Pentru a aprecia gradul de asimetrie a unei distributii statistice se folosesc o serie de indicatori, dintre care cel mai reprezentativ este coeficientul de asimetrie (Kas) propus de Karl Pearson, care poate lua valori cuprinse între -1 si +1.

 

unde:

abaterea medie patratica.

Coeficientul prezentat permite analiza asimetriei seriei în functie de semnul si nivelul acestuia:

- daca seria este perfect simetrica:

- daca seria este asimetrica:

spre stânga

spre dreapta

Coeficientul de asimetrie reflecta:

- o distributie ce tinde spre una simetrica, cu cât Kas este mai mic (mai apropiat de 0);

- o distributie moderat asimetrica, daca:

- o distributie ce tinde spre una puternic asimetrica, cu cât Kas este mai mare (mai apropiat de

În continuare, pe baza elementelor de calcul din Tabelele 6.1., 6.2. si 6.3., se determina coeficientul de asimetrie pentru fiecare varianta în parte.

Tabelul 6.2

Varianta A

Nota: Limita inferioara este inclusa în interval.

Tabelul 6.3

Varianta B

Nota: Limita inferioara este inclusa în interval.

Tabelul 6.4

Varianta C

Nota: Limita inferioara este inclusa în interval.
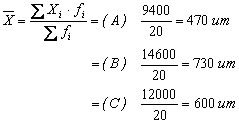
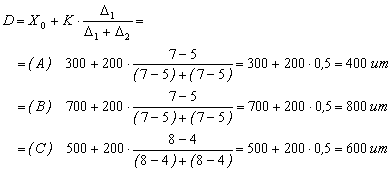
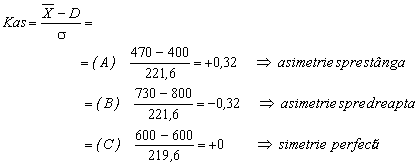