INTRODUCERE ÎN TEORIA PROBABILITĂŢII
8.1 : Câmp de evenimente : câmp de probabilitate
Fie E - o multime nevida : fie ![]() - o multime
nevida de parti ale lui E.
- o multime
nevida de parti ale lui E.
Definitie : perechea ( E , K ) este numita câmp de evenimente daca au loc
proprietatile :
- 1: ![]() ;
;
- 2: ![]() .
.
Aici prin ![]() am notat complementara multimii A .
am notat complementara multimii A .
Nota : elementele multimii K vor fi numite evenimente .
Consecinte : - 1 : însasi multimea E este un eveniment , numit evenimentul sigur .
Demonstratie : 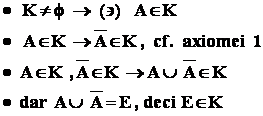
- 2: multimea vida este un eveniment , numit evenimentul imposibil
Demonstratie :
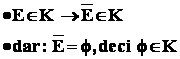
- 3 : intersectia a doua evenimente este tot un eveniment
Demonstratie :
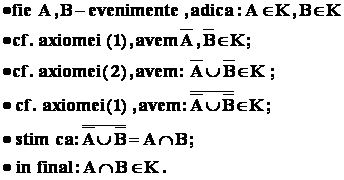
== // ==
Categorii de evenimente : - evenimentele A , B se numesc compatibile , daca
![]() ;
;
- evenimentele A , B se numesc incompatibile , daca
![]() .
.
Exemplu : consideram experienta : aruncarea unui zar omogen , cu înregistrarea
punctajului obtinut. Fie evenimentele
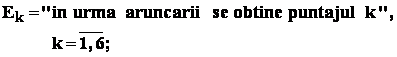 .
.
Consideram ![]() si fie K =
multimea partilor lui E : atunci cuplul
si fie K =
multimea partilor lui E : atunci cuplul
( E , K ) este câmpul de evenimente asociat experientei în cauza.
De exemplu , în acest câmp , - pentru evenimentul "
A = " punctaj numar impar "
este valabila scrierea :
A = .
- pentru evenimentul
B = " punctaj "
este valabila scrierea :
B = .
Atunci avem :
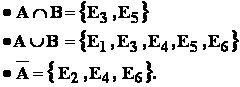
Precizare importanta : - evenimentele de forma Ek , ce corespund la situatiile fizic
posibile ce apar în cursul experientei , vor fi numite
evenimente elementare ;
- multimea tuturor evenimentelor elementare va fi numita
uneori multimea de cazuri posibile asociata experientei ;
- multimea evenimentelor elementare implicata într-un
eveniment se mai numeste si multime de cazuri favorabile
pentru avel eveniment .
De exemplu , evenimentul ![]() de mai înainte , are drept
de mai înainte , are drept
multime de cazuri favorabile , pe : ![]() .
.
Definitie : fie ( E , K ) un câmp de evenimente : o functie P : K → R se numeste functie
de probabilitate pe câmpul ( E , K ) , daca
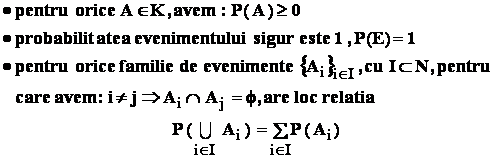
![]()
== // ==
Consecinte :
- 1 : probabilitatea oricarui eveniment A verifica relatia : 0 P ( A )
Demonstratie : fie un eveniment A ; avem
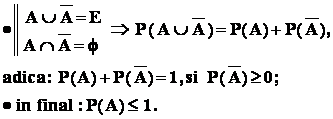
-2 : probabilitatea evenimentului imposibil este zero
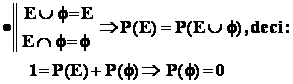
- 3: pentru orice evenimente A , B avem
![]()
Demonstratie :
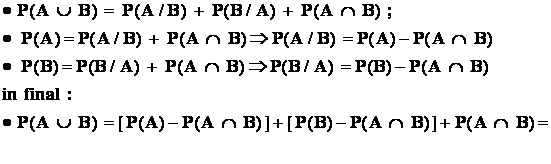
== // ==
Observare : In cazul unui câmp finit de evenimente , drept functie de probabilitate
se poate lua functia elementara de probabilitate , data de :

De exemplu : pentru experienta cu aruncarea unui zar si înregistrarea punctelor :
pentru X = " punctaj 4 " , avem drept cazuri favorabile
, deci :
![]() .
.
In cazuri în care numarul de cazuri favorabile nu poate fi utilizat , se ia în considerare
o definitie mai generala , anume :

Aici prin " masura " vom întelege " arie , greutate , volum , lungime , valoare , etc.
Exemplu : într-un patrat de latura 2 cm . este înscris un cerc .Se arunca la întîmplare un punct , în asa fel încât sa nimereasca în interiorul patratului.
Se cere probabilitatea ca punctul sa nimereasca în cercul înscris.
Rezolvare . drept " masura " vom folosi aria '
- multimea cazurilor posibile este multimea punctelor patratului , de arie 4 ;
- cercul înscris are raza 1 , deci aria sa este
- fie evenimentul : X = " punctul aruncat la întâmplare nimereste
în cerc "
- avem :
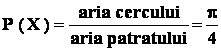 .
.
Definitie : - doua evenimente X , Y apartinând unui câmp de probabilitate dat
sunt independente , daca :
![]() ;
;
- doua evenimente X , Y apartinând unui câmp de probabilitate dat
sunt dependente , daca :
![]()
== // ==
Exemplu : In intervalul [ 0 ; 10 ] , se considera intervalele A = [ 1 ; 5 ] si B = [ 3 ; 9 ].
Se arunca la întîmplare un punct , astfel încât sa fie sigur ca nimereste în intervalul [ 0 ; 10 ].
Fie evenimentele : X = " punctul nimereste în intervalul A " ;
Y = " punctul nimereste în intervalul B " ;
Consideram , ca masura , lungimea .
Sa se stabileasca daca evenimentele X , Y sunt dependente sau independente.
Rezolvare :
avem 
Cum 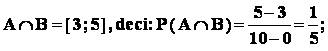
Relatia de
control a independentei , ![]() , devine :
, devine :
![]() ;
;
cum aceasta relatie este falsa , deducem ca evenimentele X , Y sunt dependente .
Definitie : evenimente conditionate ; câmp de probabilitate conditionat
Fie ( E , K , P ) - un câmp de probabilitate : fie B - un eveniment din K ,
pentru care P ( B ) ≠ 0 ;
Câmpul de evenimente conditionat de catre evenimentul B , notat
prin ( E , K , PB ) , are acelasi eveniment sigur E si aceeasi
multime de evenimente K , iar functia de probabilitate PB
este data de :
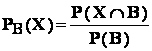 .
.
Se verifica usor ca ( E , K , PB ) verifica axiomele câmpului de evenimente .
In cazul unui câmp finit de evenimente , aceasta definitie revine la
urmatoarele :

Observare : definitia probabilitatii conditionate furnizeaza o formula de calcul
pentru probabilitatea intersectiei de evenimente dependente :
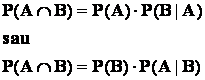 .
.
== // ==
Exemplu : într-o urna sunt 5 bile albe si 4 bile negre . Se extrag 3 bile , prin extrageri succesive : dupa fiecare extragere , bila nu se reintroduce în urna.
Se cere probabilitatea ca bilele sa fie ,în ordine : alba , neagra si alba.
Rezolvare : vom considera evenimentele :
- An = " la extragerea numarul " n " apare bila alba "
- Bk = " la extragerea numarul " k " apare bila neagra "
- X = " bilele extrase sunt , în ordine : alba , neagra si alba"
Avem evident :
![]() ,
,
deci : 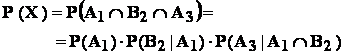
Avem : - pentru A1 , avem : 5 cazuri favorabile si 9 cazuri posibile , deci
![]() ;
;
- pentru ![]() , înseamna
ca evenimentul
, înseamna
ca evenimentul ![]() s-a produs , deci urna va
s-a produs , deci urna va
fi acum o urna cu 4 bile albe si 4 bile negre .
A
calcula ![]() , înseamna de fapt , a calcula probabilitatea
, înseamna de fapt , a calcula probabilitatea
de a extrage o bila neagra din aceasta noua urna .
Deci , ![]() ;
;
- pentru![]() , înseamna ca evenimentul
, înseamna ca evenimentul ![]() s-a
s-a
produs deja , deci urna devine o urna cu 4 bile albe si 3 bile negre .
A calcula ![]() , înseamna de fapt , a calcula probabilitatea
, înseamna de fapt , a calcula probabilitatea
de a extrage o bila alba din aceasta noua urna .
Pentru evenimentul ![]() avem 4 cazuri favorabile si 7 cazuri posibile , deci
avem 4 cazuri favorabile si 7 cazuri posibile , deci
![]() .
.
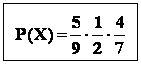 In final , .
In final , .
== // ==
REZUMAT DE FORMULE :
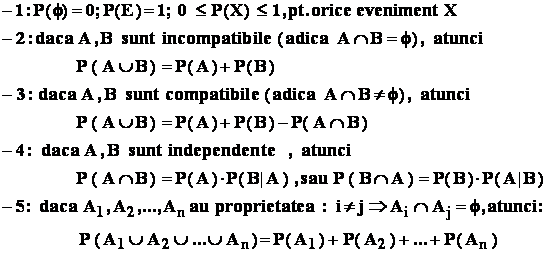
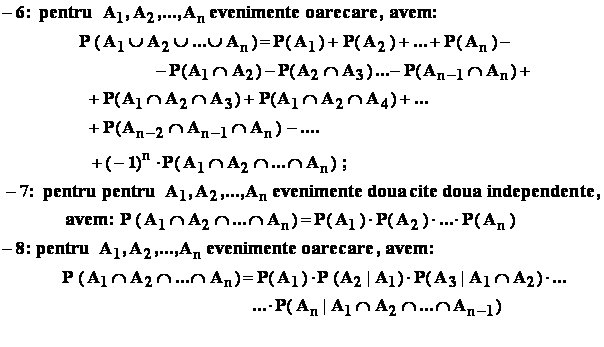
Exemplu : pentru evenimentele A , B , C prezentate în
figura , se cere ![]() ,
,
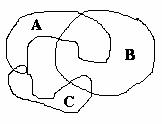
Rezolvare : avem ![]() ,deci formula ( 6 ) devine :
,deci formula ( 6 ) devine :
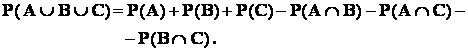
== // ==
8.2 : Formula probabilitatii totale ; formula lui Bayes
Fie ( E , K , P ) - un câmp de probabilitate : fie evenimentele
![]() .
.
Atunci : pentru orice eveniment X din K , avem :
(1) 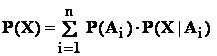 ( formula probabilitatii
( formula probabilitatii
totale ) ;
(2) 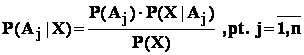
( formula lui Bayes ) .
Demonstratie :
(1) : 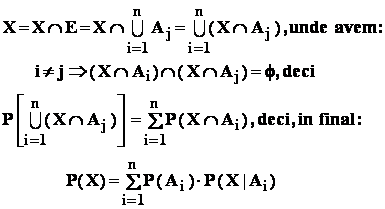
(2) : 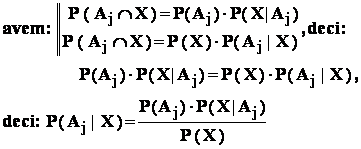
Aplicatie : se cultiva grâu de trei calitati , conform tabelului
|
calitatea |
cantitate cultivata |
putere de germinare |
|
I |
85 tone |
92 % |
|
II |
10 tone |
76 % |
|
III |
5 tone |
65 % |
Din cantitatea totala de 100 tone ,se alege la întâmplare un bob si se cultiva .
- a: se cere probabilitatea ca bobul sa germineze ;
- b : se cere probabilitatea ca un bob germinat sa fie de caliattea II .
Rezolvare : vom utiliza urmatorul sistem de evenimente:

Conform tabelului de date , avem : P (A1) = 0 , 85 ; P (A2) = 0 , 10 ; P (A3) = 0 , 05 .
Evident ca avem :
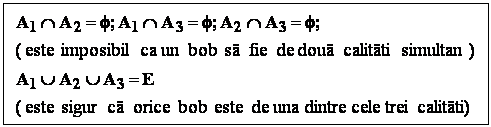
Puterile de germinare revin la urmatoarele :
![]() .
.
Atunci :
- aplicând formula probabilitatii totale :
![]()
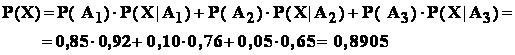
deci din amestecul de 100 tone , germineaza 89 , 05 % dintre boabe .
== // ==
9.3 : Scheme probabilistice clasice
9.3.1: Schema lui Bernoulli :
Se considera o urna cu bile albe si negre : presupunem ca se cunoaste
- p = procentul de bile albe din urna ;
- q = procentul de bile negre din urna ;
avem evident : p , q > 0 ; p + q =1 .
Experienta efectuata este urmatoarea :
- se fac " n " extrageri ; dupa fiecare extragere , bila extrasa
se reintroduce în urna ( " extrageri cu revenire " sau
" prin probe independente" ).
Observare : extragerile " cu revenire " au ca efect faptul ca
dupa fiecare extragere , urna revine la starea
initiala ;
- în urma extragerilor , se înregistreaza valoarea indicatorului'
.

Evenimentele fundamentale asociate experientei vor fi :
![]()
Evenimentele ![]() au
proprietatile urmatoare ;
au
proprietatile urmatoare ;
-
sunt doua câte doua incompatibile : ![]() ;
;
- reuniunea lor este evenimentul sigur :
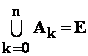 ;
;
- probabilitatea lor se calculeaza cu formula :
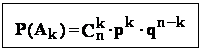
== // ==
Aplicatie : într-o urna sunt : 75 % bile albe si 25 % bile negre . Din urna se extrag ,
cu revenire , 12 bile .
Se cere probabilitatea ca :
- a: printre cele 12 bile extrase sa fie 9 bile albe ;
- b: printre cele 12 bile extrase sa fie cel mult 6 bile albe ;
- c: printre cele 12 bile extrase sa fie cel putin 8 bile albe ;
- d: numarul de bile albe aflate printre cele 12 bile extrase sa fie
cuprins între 5 si 11 ;
Rezolvare : comparând datele problemei cu notatiile modelului , gasim :
n = 12 ; p = 0,75 ; q = 0,25.
![]()
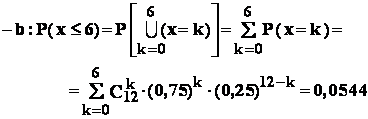
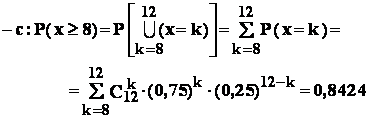
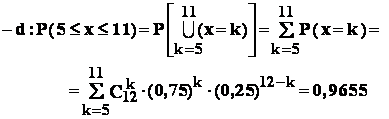
== // ==
Problema : în legatura cu aplicatia precedenta , se considera evenimentele
A = " numarul de bile extrase este 8 "
B = " numarul de bile extrase este
Stabiliti daca evenimentele A , B sunt dependente sau independente .
Rezolvare :
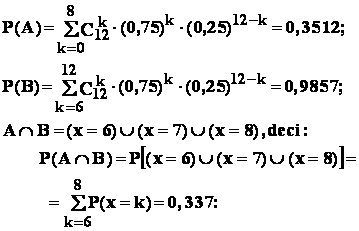
Relatia de control
a independentei , anume : ![]() , devine
, devine
0, 3512 ∙0,9857 = 0,337 ,
adica : 0, 3462 = 0 , 337 .
Fiind falsa , deducem ca evenimentele A , B sunt dependente .
Problema : dintr-o urna cu 68% bile albe si 32% bile negre se fac extrageri , cu revenire,
de câte 15 bile . Se cere numarul cel mai probabil de bile albe aflate printre cele 15 bile extrase .
Rezolvare : notam : x = numarul de bile albe aflate printre cele 15 bile extrase ;
avem : ![]() .
.
Problema noastra revine la urmatoarea :
![]()
Deoarece variabila " k ' este numar întreg , vom folosi principiul combinatorial , pentru probleme de maxim , anume :
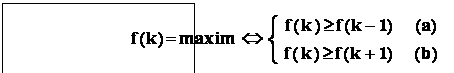
Relatia ( a) :
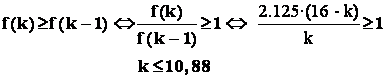
Relatia ( b ) :
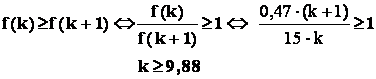
In final , din :
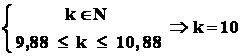 .
.
Raspuns : cel mai frecvent , printre cele 15 bile extrase vor fi 10 bile albe .
== // ==
Problema : dintr- o urna cu bile albe si negre se fac extrageri , cu revenire ,
de câte 20 de bile . Se constata ca varianta : " printre cele 20 de bile extrase se afla 17 bile albe " apare mai frecvent decât orice alta varianta.
Ce se poate spune despre procentul de bile albe din acea urna?
Rezolvare : cu notatiile deja cunoscute , avem ;
![]() .
.
Se stie ca :
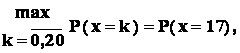
ceeace , în conformitate cu principiul combinatorial , revine la :
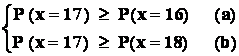
Relatia (a) :
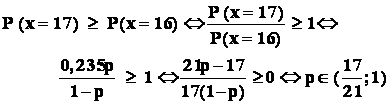
Relatia (b) :
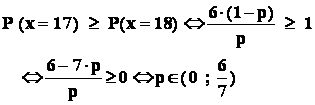
In final , din :
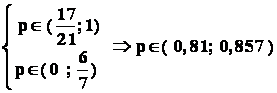 .
.
Raspuns :
![]()
== // ==
9.3.2 : Schema urnei cu bile albe si negre : extrageri fara revenire
Datele problemei sunt urmatoarele : avem o urna pentru care se cunoaste :
- a = numarul de bile albe din urna ;
- b = numarul de bile negre din urna .
Din urna se extrag " n " bile; dupa fiecare extragere , bila extrasa nu se reintroduce în urna , astfel ca la fiecare extragere , compozitia urnei se modifica.
Observare : acest mod de extragere este echivalent cu extragerea simultana a întregului lot de " n " bile.
![]() In urma experientei se consemneaza
valoarea indicatorului :
In urma experientei se consemneaza
valoarea indicatorului :
Evenimentele fundamentale asociate experientei sunt :
![]() .
.
Evenimentele ![]() au proprietatile
urmatoare ;
au proprietatile
urmatoare ;
-
sunt doua câte doua incompatibile : ![]() ;
;
- reuniunea lor este evenimentul sigur :
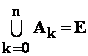 ;
;
- probabilitatea lor se calculeaza cu formula :
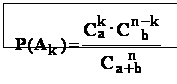
== // ==
Aplicatie : într-o urna sunt 20 de bile albe si 15 bile negre : se extrag 10 bile ; extragerile sunt fara revenire . In urma extragerii se consemneaza valoarea indicatorului
x = numar de bile albe aflate printre cele 10 bile extrase
Se cere probabilitatea ca :
- 1: numarul de bile albe sa fie de cel mult 7 ;
- 2: numarul de bile albe sa fie de cel putin 3 ;
- 3: numarul de bile albe sa fie cuprins între 2 si 8.
Rezolvare : identificând parametrii problemei , constatam ca avem :
a = 20 ; b = 15 ; n = 10
-1: se cere
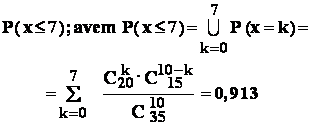
- 2 : se cere :
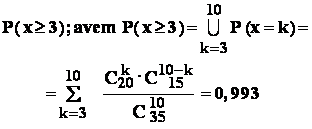
- 3 : se cere :
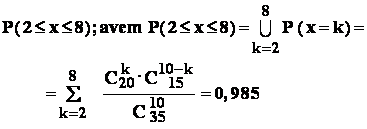
Aplicatie : în legatura cu problema precedenta : sa se determine numarul cel mai probabil de bile albe aflate printre cele 10 bile extrase , adica valoarea lui " k " ,
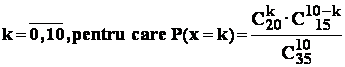 este maxima.
este maxima.
Conform principiului combinatorial , avem:
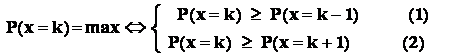
- Relatia (1) :
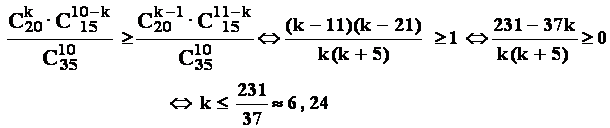
- Relatia (2) :
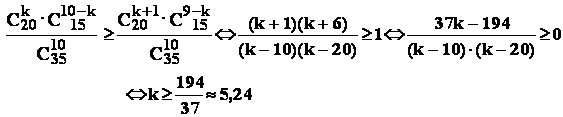
In final , din relatiile : 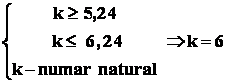 .
.
Raspuns : printre cele 10 bile extrase , cel mai frecvent apar 6 bile albe.
Aplicatie : Intr-o urna sunt 50 de bile , albe si negre . Se fac extrageri , fara revenire , de câte 15 bile si se înregistreaza valorile indicatorului:
x= numar de bile albe aflate printre cele 15 bile extrase .
Se constata ca varianta care apare cel mai frecvent este : ( x = 12 ).
Ce se poate spune despre numarul de bile albe din urna ?
Rezolvare : sa notam cu a = numarul de bile albe din urna .
Notam f(k ) = P( x= k ) , deci :
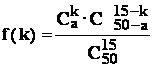 .
.
Avem conditia : f (12) f(k) , pentru orice k = ![]() ; conform principiului combinatorial , aceasta revine la
conditiile
; conform principiului combinatorial , aceasta revine la
conditiile
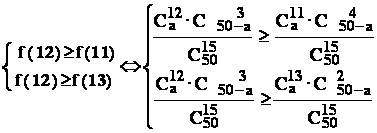
adica :
![]()
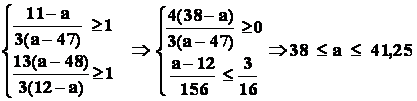
In final : ![]() .
.
== // ==
9.3.3 : Schema urnei cu bile de mai multe culori :
\extrageri cu revenire .
Datele problemei sunt urmatoarele :
|
culoarea |
C1 |
Ci |
Cn |
||
|
% de bile |
p1 |
pi |
pn |
unde sunt valabile conditiile :
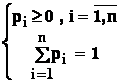 .
.
Din urna se extrag , cu revenire , " m " bile , înregistrându-se culorile acestora.
Evenimentele fundamentale corespunzatoare au aspectul:

Evident ca avem :
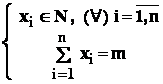 .
.
Formula :
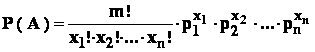
== // // ==
9.3.4 : Schema urnei cu bile de mai multe culori :
\extrageri cu revenire .
Datele problemei sunt urmatoarele :
|
culoarea |
C1 |
Ci |
Cn |
||
|
numar de bile corespunzator |
k1 |
ki |
kn |
.
Din urna se extrag , fara revenire , " m " bile , înregistrându-se culorile acestora.
Evenimentele fundamentale corespunzatoare au aspectul:
A = " printre cele "m" bile extrase , sunt : x1 bile de culoare C1 ;
x2 bile de culoare C2,. , xn bile de culoare Cn " ,
Evident ca avem : ![]() =m .
=m .
Formula
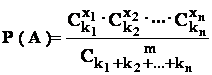 .
.
== // ==
9.4 : VARIABILE ALEATOARE
Fie ( E , K , P ) - un câmp de probabilitati ;
Functia f : E R se numeste variabila aleatoare , daca are loc proprietatea :
![]()
Clasificarea variabilelor aleatoare :
- daca imaginea functiei f este formata numai din puncte
izolate , f se numeste variabila aleatoare discreta ( pres-
curtat : VAD ) ;
- daca imaginea functiei f este un inteval ,
f se numeste variabila aleatoare continua .
9.4.1: Variabile aleatoare discrete :
Fiind formata numai din
puncte izolate , imaginea lui f are aspectul
![]() ;
;
vom considera pentru simplificarea notatiilor , ca :
![]() .
.
Precizare : -numerele ![]() vor fi numite argumentele variabilei aleatoare " f
" .
vor fi numite argumentele variabilei aleatoare " f
" .
- multimile :
![]()
vor fi numite evenimentele fundamentale asociate variabilei aleatoare " f " .
- sistemul de evenimente ![]() are proprietatea :
are proprietatea :
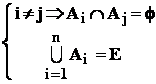 ;
;
= pentru ![]() vom nota : pi = P(Ai) .
Sistemul de probabilitati
vom nota : pi = P(Ai) .
Sistemul de probabilitati ![]()
are proprietatea :
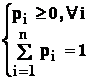
- forma redusa a variabilei aleatoare " f " : pentru aplicatiile practice ,
variabila aleatoare discreta " f " va fi notata :
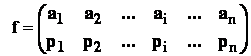 .
.
== // ==
9.4.2 : Vector aleator : variabile aleatoare independente
Pe un câmp de probabilitate se definesc simultan doua variabile aleatoare discrete ,
" f " si " g " : presupunem ca aceste variabile au forma redusa precizata mai jos :
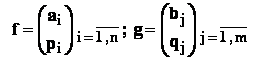 ;
;
reamintim ca au loc proprietatile :
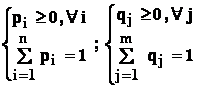 .
.
Probabilitatile repartitiei comune a variabilelor f , g :
pentru ![]() notam :
notam : ![]() ;
;
valorile ![]() vor fi numite probabilitatile
repartitiei comune a variabilelor f , g .
vor fi numite probabilitatile
repartitiei comune a variabilelor f , g .
Acestea au proprietatile evidente :
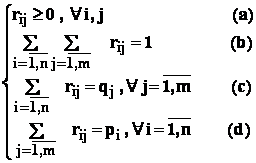 ;
;
Demonstratii :
- a: evident , orice probabilitate este o ;
- b: avem :
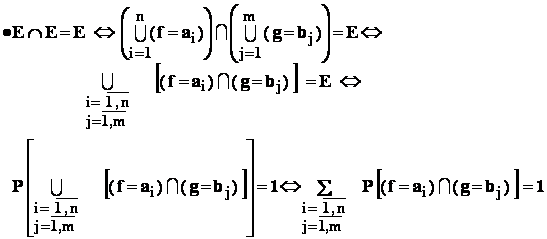
adica , în final , ![]() .
.
- c: avem urmatoarele :
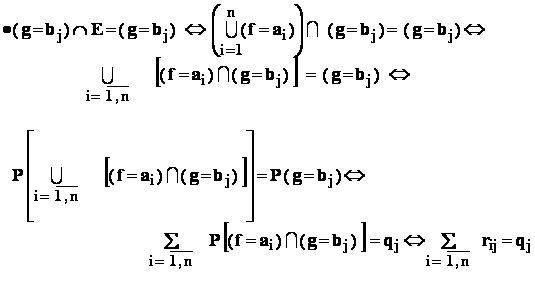
- d: avem urmatoarele :
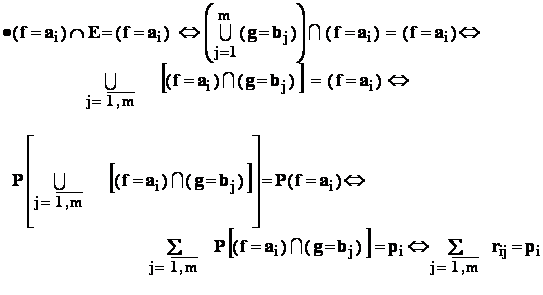
== // ==
Definitie : - variabilele aleatoare discrete f , g sunt independente , daca
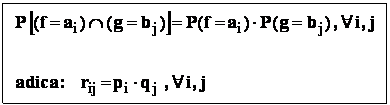
: - variabilele aleatoare discrete f , g sunt dependente , daca
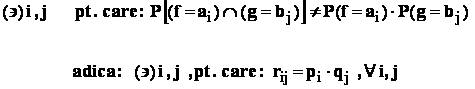
== // ==
Exemplu : variabilele aleatoare discrete f , g de mai jos sunt independente :
sa se scrie repartitia lor comuna.
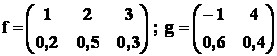 .
.
Rezolvare :
|
b1=- 1 |
b2= 4 | ||
|
a1=1 |
r11= 0,2 ∙0,6 |
r12= 0,2∙0,4 |
p1= 0,2 |
|
a2=2 |
r21= 0,5∙0,6 |
r21= 0,5∙0,4 |
p2= 0,5 |
|
a3=3 |
r31= 0,3∙0,6 |
r31= 0,3∙0,4 |
p3= 0,3 |
|
q1= 0,6 |
q2= 0,4 |
Precizare : - o pereche de variabile aleatoare ( f , g ) formeaza un vector aleator ;
- componentele f , g ale vectorului aleator ( f , g) se numesc
variabile marginale ale lui ( f , g) ; argumentele variabilelor marginale se
numesc argumente marginale ; probabilitatile variabilelor marginale se
numesc probabilitati marginale ;
Problema : un vector aleator are repartitia :
|
b1=- 1 |
b2= 4 | ||
|
a1=1 |
r11= 0,2 ∙0,6 |
r12= 0,2∙0,4 |
p1= 0,2 |
|
a2=2 |
r21= 0,5∙0,6 |
r21= 0,5∙0,4 |
p2= 0,5 |
|
a3=3 |
r31= 0,3∙0,6 |
r31= 0,3∙0,4 |
p3= 0,3 |
|
q1= 0,6 |
q2= 0,4 |
|
b1 = 2 |
b2 = 5 |
|
|
a1=1 |
r11= 0,25 |
r12= 0,15 |
|
a2= 3 |
r21= 0,40 |
r21= 0,20 |
- se cer variabilele aleatoare marginale , norare A si B ;
- sunt variabilele aleatoare A , B independente ?
Rezolvare :

Controlul independentei :
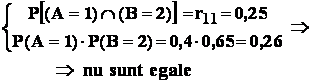
deci A , B sunt variabile aleatoare dependente .
![]()
9.4.3 : Operatii cu variabile aleatoare :
Functii de o variabila aleatoare discreta
Fiind data variabila aleatoare f : E R si o functie G: R R,
avem : (G° f ) : E R , în sensul compunerii obisnuite de functii .
Aceasta definitie revine la urmatoarele :
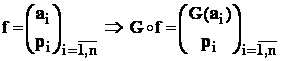 .
.
Exemple : fie 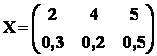 ;
;
- avem :
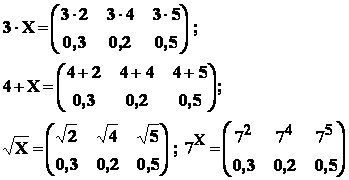
Operatii cu doua sau mai multe variabile aleatoare discrete
Fie vectorul aleator ( X ,Y ) , unde :
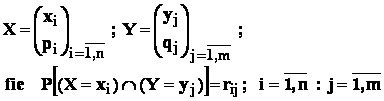
Fie o functie F: RxR R ; atunci variabila F( X , Y ) este data de :
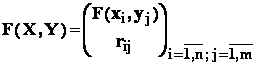 .
.
De exemplu : fie vectorul aleator ( X , Y ) , cu repartitia
|
y1=1 |
y2=3 | ||
|
x1= 2 |
r11=0,2 |
r12 = 0,3 |
p1=0,5 |
|
x2= 4 |
r21=0,4 |
r22 = 0,1 |
p2=0,5 |
|
q1=0,6 |
q2=0,4 |
Se cere repartitia variabilei aleatoare Z = 3∙X + 2∙Y .
Rezolvare ![]()
- tabelul argumentelor lui Z :
|
y1=1 |
y2=3 | ||
|
x1= 2 |
p1=0,5 |
||
|
x2= 4 |
p2=0,5 |
||
|
q1=0,6 |
q2=0,4 |
Asadar , repartitia variabilei Z este :
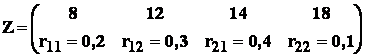 .
.
== // ==
Exemplu: fie vectorul aleator
|
y1=1 |
y2=2 | ||
|
x1= 1 |
r11=0,2 |
r12 = 0,3 |
p1=0,5 |
|
x2= 2 |
r21=0,4 |
r22 = 0,1 |
p2=0,5 |
|
q1=0,6 |
q2=0,4 |
Se cere repartitia variabilei aleatoare T = | X - Y | .
Rezolvare : avem tabelul de argumente ale lui T :
|
y1=1 |
y2=2 | ||
|
x1= 1 |
p1=0,5 |
||
|
x2= 2 |
p2=0,5 |
||
|
q1=0,6 |
q2=0,4 |
Asadar , repartitia lui T este :
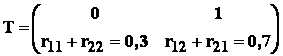 .
.
== // ==
9.4.4 : Momentele unei variabile aleatoare discrete
Definitie : fie variabila aleatoare
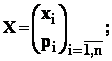
definim : - media variabilei aleatoare X :
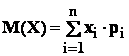 ;
;
Observare : daca nu sunt posibile confuzii , vom nota media cu " m " ;
- dispersia variabilei aleatoare X ;
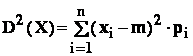 ;
;
Observare
: cantitatea ![]() se numeste abaterea medie
se numeste abaterea medie
standard ( sau : abaterea medie patratica) a variabilei X .
- momentul initial de ordin k al variabilei X este definit prin :
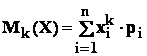 ;
;
Observare : media lui X este chiar momentul initial de ordin 1 al lui X .
- momentul centrat de ordin k al variabilei X este definit prin :
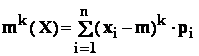 ;
;
Observare : dispersia lui X este chiar momentul centrat de ordin 2
al lui X .
== // ==
Proprietatile mediei :
- a: fie k - o
![]()
Observare :
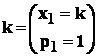 ,
,
deci M(k) = x1∙p1 = k .
- b: fie k - o
![]()
In adevar , fie :
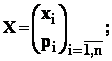 atunci
atunci 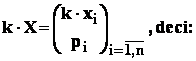
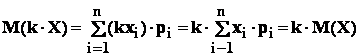 .
.
- c : fie X , Y - variabile aleatoare oarecare ( dependente sau independente )
avem :
![]()
In adevar, avem ;
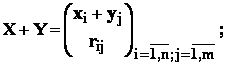
deci :
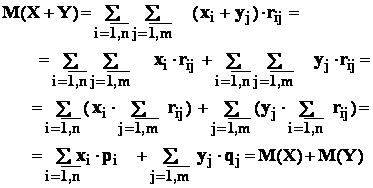
- d : fie X , Y - variabile aleatoare independente : atunci
![]()
In adevar , deoarece X , Y sunt independente , repartitia lor comuna este :
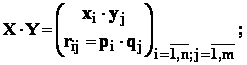
atunci ,
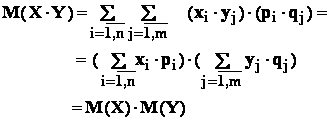
Observare importanta : relatia : M(X∙Y) = M(X)∙M(Y) poate fi adevarata
si pentru variabile aleatoare X , Y - dependente.
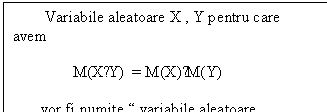
Deci : unele dintre variabilele aleatoare necorelate sunt independente , altele sunt
dependente.
PROPRIETATILE DISPERSIEI :
- a : expresia dispersiei în functie de momente initiale :
![]()
In adevar :
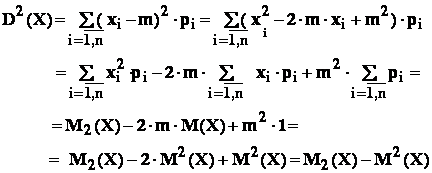
- b : dispersia unei constante este zero :
în adevar , avem ;
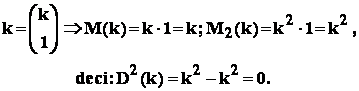
Observare importanta : pentru variabile aleatoare discrete , este adevarata si afirmatia
reciproca , anume : daca dispersia unei variabile aleatoare este
zero , atunci acea
variabila este ( de fapt ) o
mai mult , cu cât dispersia unei variabile aleatoare este mai mica ,
cu atât
acea variabila este mai aproape de o
- c : dispersia sumei sau diferentei de variabile aleatoare independente
este egala cu suma dispersiilor :
![]()
In adevar : sa tratam numai cazul diferentei de variabile ; avem
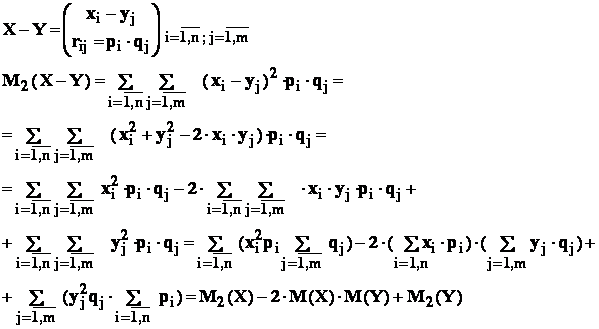
Asadar , am aratat ca :
![]()
Stim ca : M(X-Y) = M(X) - M(Y) , deci :
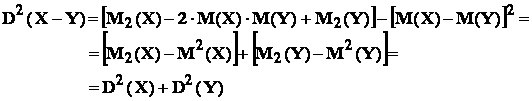
- d : pentru k =
![]()
Demonstratia este imediata .
== // ==
9.4.5 : INDICATORI DE DEPENDENTA
Definitie : covarianta variabilelor aleatoare X , Y este definita prin :
![]()
Observare : se arata usor ca :
![]()
Observare : - dupa cum s-a aratat , avem :
X , Y - independente M( X∙Y ) = M(X)∙M(Y) ,
deci : X , Y - independente cov ( X , Y ) = 0 .
- reciproca nu este însa adevarata : este deci posibil sa avem
cov ( X , Y ) = 0 , dar X ,Y sa fie dependente .
Definitie : variabilele X , Y pentru care avem cov ( X , Y ) = 0 , se
numesc variabile necorelate .
Proprietatile covariantei
Avem :
![]()
Demonstratie : avem
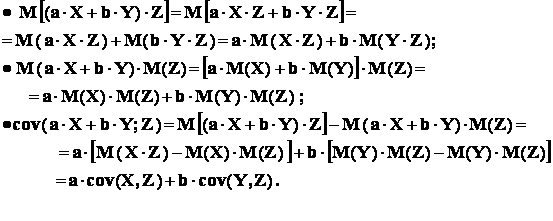
Definitie : coeficientul de corelatie al variabilelor X , Y este definit de
relatia :
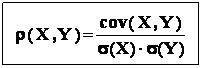
Coeficientul de corelatie are aproximativ aceleasi proprietati ca si covarianta , adica

Proprietatea speciala , care confera coeficientului de corelatie un rol special ,
este urmatoarea :
![]()
Nota : variabila normata corespunzatoare variabilei aleatoare X este :
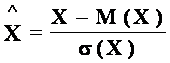 ;
;
O variabila normata are proprietatea :
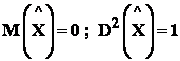 .
.
In adevar ,
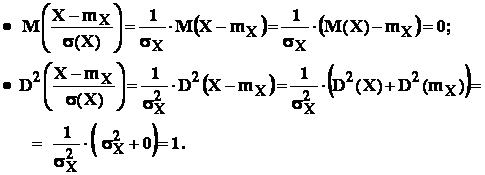
Observare : coeficientul de corelatie are caracter liniar , lucru ce este ilustrat
si de catre urmatoarele studii :
- a : fie X , Y variabile aleatoare ; fie a ,b - numere reale , a ≠ 0 :
sa calculam ( Y ; a∙X+ b) ;
Rezolvare :
![]()
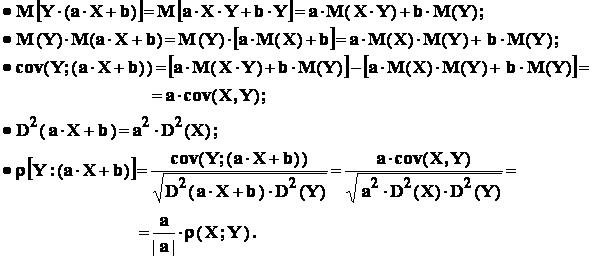
In final :
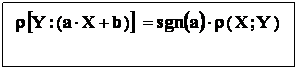
- b : fie X - variabila aleatoare , si a , b - numere reale , a ≠ 0 ;
avem
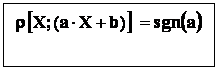
Relatia rezulta din formula precedenta , cu considerarea faptului ca (X ; X ) = 1.
- c : fie X , Y - variabile aleatoare , si a ,b , c , d - numere reale ; a ≠ 0 ; c ≠ 0 :
avem :
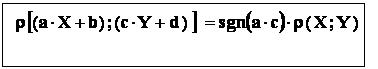
Si aceasta relatie rezulta din punctul (1) .
== // ==
9.4.6 : Variabile discrete clasice
- a : Variabila discreta cu repartitie uniforma
Prin definitie , variabila discreta cu repartitie uniforma , care
are ca multime de argumente , multimea ![]()
este variabila :
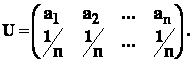
Observare : - media variabilei uniforme :
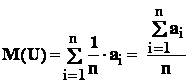 - chiar media
aritmetica a
- chiar media
aritmetica a
argumentelor variabilei .
- momentul initial de ordin 2 al variabilei uniforme ;
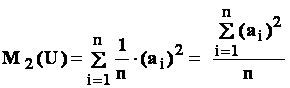 ;
;
- dispersia variabilei uniforme :
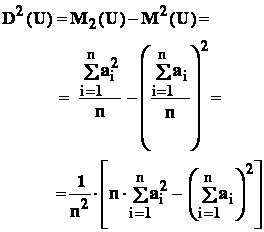
- b : Variabila aleatoare cu repartitie binomiala :
Variabila aleatoare cu repartitie binomiala are repartitia :
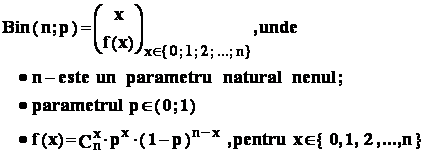
Vom demonstra urmatoarele :
- 1 : f(x ) - este într-adevar o functie de probabilitate ,
adica :
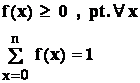 ;
;
- 2 :media variabilei X este : M(X) = n∙p ;
- 3 :dispersia variabilei X este : D2(X) = n∙p∙( 1- p ) ;
- 4 :modul variabilei X este numarul întreg " k " , pt.
care avem :
![]() .
.
Demonstratii :
fie functia auxiliara g( t ) = [ p∙t + ( 1-p) ] n , unde " t " este un parametru
real fara nici o semnificatie .
Observare : folosind dezvoltarea lui g(t) , cu ajutorul binomului Nuwton , gasim
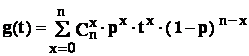
- 1: avem evident f(x) 0 , pentru orice x ;
în plus ,
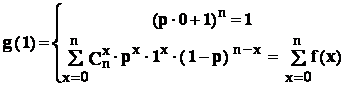
Deci : 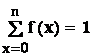 .
.
- 2: avem
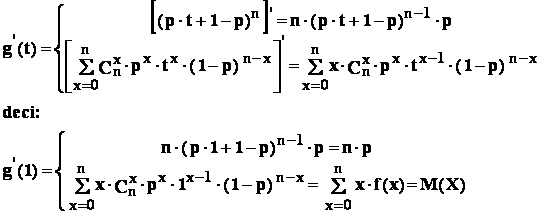
-3 : avem

asadar : ![]()
Dar stim ca : D2(X) = M2(X) - (M(X))2 , deci :
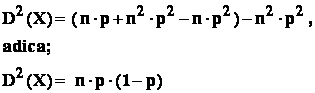
- 4 : modul k al variabilei X este argumentul " x " al variabilei , pentru care functia de probabilitate f(x) ia valoarea maxima : folosind principiul combinatorial , gasim :
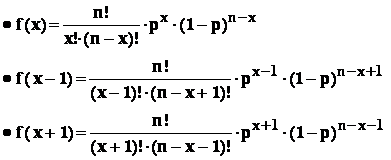
Conditiile de maxim devin :
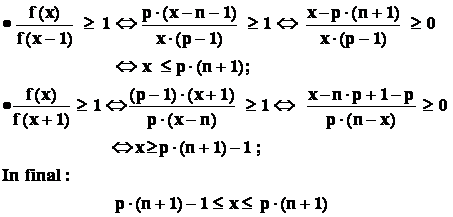
9.5 : VARIABILE ALEATOARE CONTINUE
Reamintim ca , în cazul unei variabile aleatoare continue , X , data de o functie f definita pe evenimentul sigur al câmpului de probabilitate , Im(f) este un interval ( a ; b ) .
Aceasta conditie nu este suficienta pentru lucrul cu variabile aleatoare continue ;
dintre alte conditii importante , dar care depasesc mult nivelul acestei expuneri ,
vom folosi una , anume :
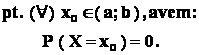
- Forma generala a unei variabile aleatoare continue ;
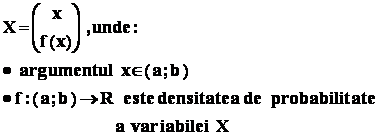
Densitatea de probabilitate are proprietatile :
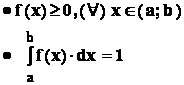 .
.
- Calculul probabilitatii unor evenimente , folosind densitatea de probabilitate :
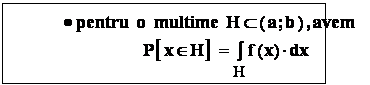 avem :
avem :
De exemplu :
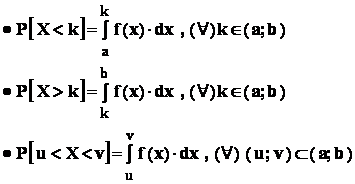
Majoritatea definitiilor
reproduc acum definitiile date în cazul variabilelor discrete , înlocuind
" ![]() " , prin "
" , prin "![]() " .
" .
De exemplu :
- fie variabila aleatoare continua
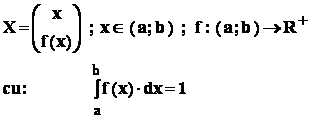
- media variabilei X :
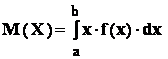
- momentul initial de ordin 2 :
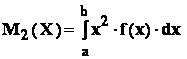
- momentul centrat de ordin 2 ( adica dispersia variabilei X ) :
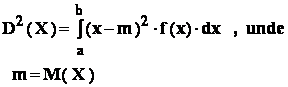
Observare importanta : pentru variabila aleatoare X ,
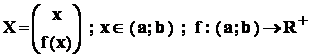
consideram ca : P ( X a ) = 0 ; P ( X b ) = 0
- din cauza proprietatii : P( X = k ) = 0 , pentru orice " k " din ( a ; b ) ,
nu se face deosebire între interval închis si interval deschis , adica
P ( u < X < v ) = P ( u X < v ) = P ( u < X v ) = P ( u X v ) ;
P ( X > k ) = P ( X k ) , etc .
== // ==
Functia de repartitie a unei variabile aleatoare continue .
Fie variabila aleatoare :
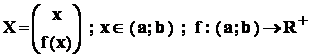
Functia de repartitie a variabilei X este o functie F : R R , data de
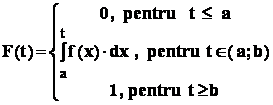 ;
;
Cu ajutorul functiei de repartitie , se pot calcula probabilitati de evenimente în care este implicat X , de exemplu :
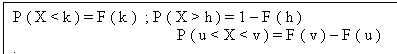
Dar proprietatea fundamentala a functiei de repartitie este urmatoarea :

Aplicatie : fie variabila aleatoare
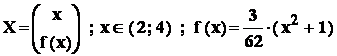 ;
;
se cere repartitia variabilei aleatoare Y = X2 .
Vom folosi functiile de repartitie : astfel , fie
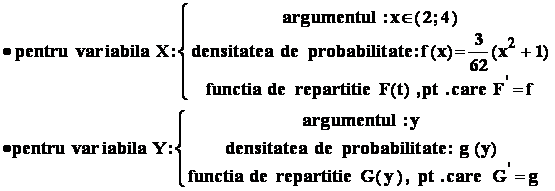
Avem urmatoarele etape :
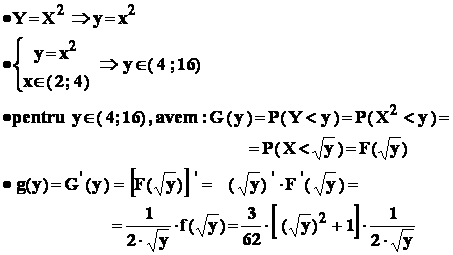
In final ,
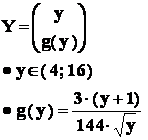
== // ==
Interval de încredere pentru o variabila aleatoare continua :
Fie variabila aleatoare X , pepartizata în intervalul ( a ; b ) ;
fie ![]() .
.
Atunci : intervalul de încredere pentru variabila X , cu coeficientul de încredere " p "
este intervalul ( u ; v ) ![]() ( a ; b ) , pentru
care "
( a ; b ) , pentru
care "
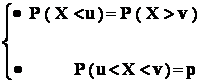 ;
;
Observare :
- din relatiile :
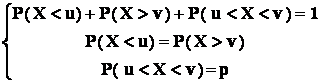
rezulta :
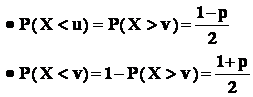 ;
;
Asadar , notând cu F - functia de repartitie a variabilei X , avem :
- capatul din stânga al intervalului de încredere , cu coeficientul de
încredere " p " , este solutia ecuatiei
![]() ;
;
- capatul din dreapta al intervalului de încredere , cu coeficientul de
încredere " p " , este solutia ecuatiei
![]() .
.
9.6 : Variabila aleatoare cu repartitie normala
Variabila aleatoare cu repartitie normala este data de :
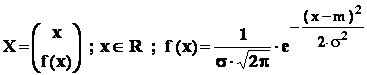 ,
,
unde m , σ - sunt parametri , σ > 0 .
In mod curent , variabila aleatoare normala de parametri m , σ este notata
prin N (m , σ ) .
In legatura cu aceasta variabila prezentam pe scurt o serie de rezultate :
- 1 : media variabilei aleatoare N (m , σ ) este egala cu " m " ;
- 2 : dispersia variabilei aleatoare N (m , σ ) este egala cu "σ " ;
- 3: daca X = N (m , σ ) , atunci , pentru Y = a∙X + b avem :
![]()
Observare : variabila aleatoare normala de parametri m = 0 ; σ = 1 ,
se numeste variabila aleatoare normala normata ;
avem rezultatul :
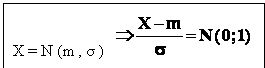
- 4 : pentru n > 30 , variabila binomiala Bin ( n ; p ) are o repartitie aproximativ
egala cu
![]() .
.
- 5: - intervalul de încredere , cu coeficientul de încredere p = 0 , 95 , pentru
variabila aleatoare N ( 0 ; 1 ) , este : ( - 1, 96 ; 1, 96 ) ;
- intervalul de încredere , cu coeficientul de încredere p = 0 , 95 , pentru
variabila aleatoare N ( 0 ; 1 ) , este : ( - 2, 58 ; 2, 58) .
|