ALTE DOCUMENTE
|
||||||||||
MATRICI
Definitie Fie M=![]() ,N=
,N=![]() multimea primelor m respectiv n, numere naturale nenule.Se
numeste matrice de tip (m,n) functia A:MxN C definita
prin tabloul A=
multimea primelor m respectiv n, numere naturale nenule.Se
numeste matrice de tip (m,n) functia A:MxN C definita
prin tabloul A=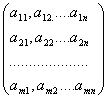 notata prescurtat A=(aij)
notata prescurtat A=(aij)![]() unde aij
unde aij ![]() C(multimea numerelor complexe).Multimea tuturor matricelor de
tip (m,n)se noteaza cu Mmn(C) unde m reprezinta numarul de linii si
n numarul de coloane .
C(multimea numerelor complexe).Multimea tuturor matricelor de
tip (m,n)se noteaza cu Mmn(C) unde m reprezinta numarul de linii si
n numarul de coloane .
Daca m=n, o matrice [n care numarul de linii este egal cu numarul de coloane se numeste matrice patratica de ordin n.
Matrici egale Fie A![]() Mmn(C), A aij)
Mmn(C), A aij)![]() si B
si B![]() Mmn(C), B=(bij)
Mmn(C), B=(bij)![]() Atunci A=B aij=
bij oricare ar fi i=
Atunci A=B aij=
bij oricare ar fi i=![]() , j=
, j=![]() .
.
Adunarea matricelor A+B=C
unde C=(cij)![]() unde cij=aij+bij oricare ar fi i=
unde cij=aij+bij oricare ar fi i=![]() ,j=
,j=![]() de numeste suma dintre matricele A si B.
de numeste suma dintre matricele A si B.
Proprietati: 1)Adunarea este
asociativa :(A+B)+C=A+(B+C) ![]() A,B,C
A,B,C ![]() Mmn(C)
Mmn(C)
2)Adunarea este
comutativa: A+B=B+A ,![]() A,B
A,B![]() Mmn(C)
Mmn(C)
3)Matricea cu toate
elementele 0(zero),notata cu O ,O![]() Mmn(C),este elementul neutru pentru adunare.
Mmn(C),este elementul neutru pentru adunare.
4)Orice matrice A![]() Mmn(C) are un opus notat -A
Mmn(C) are un opus notat -A![]() Mmn(C) astfel [ncat A+(-A)=(-A)+A=0.
Mmn(C) astfel [ncat A+(-A)=(-A)+A=0.
Observatie: Se aduna numai matrici de acelasi tip.
Inmultirea matricilor
Se [nmultesc doua matrici A Mmn(C) si B Mnp(C) numai daca numarul de
coloane ale lui A este egal cu numarul de linii ale lui B si AB=C unde C![]() Mmp(C) si daca A=(aij)
Mmp(C) si daca A=(aij)![]() ,B=(bjk)
,B=(bjk)![]() atunci C=(cik)
atunci C=(cik)![]() .
.
Pe scurt "se [nmultesc liniile cu coloanele "
cik=ai1b1k+ai2b2k+...+ainbnk=![]()
Proprietati 1)Inmultirea matricilor este asociativa:
(AB)C=A(BC) daca A![]() Mmn(C),B
Mmn(C),B![]() Mnp(C),C
Mnp(C),C![]() Mpq(C)
Mpq(C)
2)Inmultirea matricilor nu este comutativa,[nmultirea este asemanatoare cu compunerea functiilor.
3)Inmultirea este distributiva fata de adunare :
Daca A![]() Mmn(C);B,C
Mmn(C);B,C![]() Mnp(C) atunci A(B+C)=AB+AC
Mnp(C) atunci A(B+C)=AB+AC
Daca A,B![]() Mmn(C) si C
Mmn(C) si C![]() Mnp(C) atunci (A+B)C=AC+BC
Mnp(C) atunci (A+B)C=AC+BC
4)In multimea
Mn(C) matricilor patratice exista matricea In=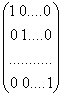
patratica de
ordinul n ce reprezinta elementul neutru fata de [nmultire,adica AIn=InA=A ![]() A
A![]() Mn(C).
Mn(C).
Inmultirea cu scalari a matricilor:
Fie A![]() Mmn(C),A=(aij)
Mmn(C),A=(aij)![]() si a
si a![]() C atunci aA=B, B=(bij)
C atunci aA=B, B=(bij)![]() unde bij=a aij
unde bij=a aij
Proprietati: 1)Daca A![]() Mmn(C) atunci 1 A=A
Mmn(C) atunci 1 A=A
2) Daca A![]() Mmn(C)si a,b
Mmn(C)si a,b![]() C atunci (a+b)A=aA+bA
C atunci (a+b)A=aA+bA
3) Daca A![]() Mmn(C) si a,b
Mmn(C) si a,b![]() C atunci (ab)A=a(bA)
C atunci (ab)A=a(bA)
4) Daca A,B![]() Mmn(C)si a
Mmn(C)si a![]() C atunci a(A+B)=aA+aB
C atunci a(A+B)=aA+aB
5) Daca A![]() Mmn(C),B
Mmn(C),B![]() Mnp si a
Mnp si a![]() C atunci a(AB)=(aA)B
C atunci a(AB)=(aA)B
Matricea transpusa notata cu At -se schimba [n A liniile [n coloane.
Exercitii rezolvate :
Fie A=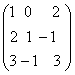
![]() M3(Q).Daca f(x)=X2+3x+I3,sa
se calculeze f(A).
M3(Q).Daca f(x)=X2+3x+I3,sa
se calculeze f(A).
REZOLVARE: f(A)=A2+3A+I3=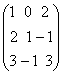
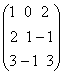 +3
+3 +
+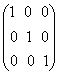 =
=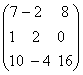 +
+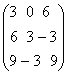 +
+ => f(A)=
=> f(A)=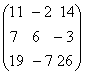
Fie
matricea A=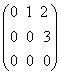 .Sa se calculeze
(I+A)n,n
.Sa se calculeze
(I+A)n,n![]() N* iar I=
N* iar I=  .
.
REZOLVARE: Se poate aplica binomul lui
(I+A)n=C![]() In+C
In+C![]() In-1A+C
In-1A+C![]() In-2A2+....+C
In-2A2+....+C![]() An
An
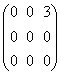
Dar A2 =A A=
 =
=
A3=A2 A=
 =
=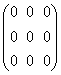 =0
=0
Deci An=0 ![]() n
n![]() 3 n
3 n![]() N si (I+A)n=
N si (I+A)n= +n
+n +
+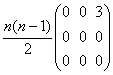 +..+0
+..+0
In final (I+A)n=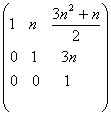
Observatie:In
general daca A=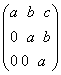 ,a,b,c
,a,b,c![]() R atunci A=
R atunci A= +
+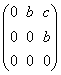 sau A=I+B unde B=
sau A=I+B unde B= .Se constata ca B3 =0 si deci Bn=0
.Se constata ca B3 =0 si deci Bn=0 ![]() n
n![]() 3 n
3 n![]() N si atunci An=(I+B)n.
N si atunci An=(I+B)n.![]()
Fie matricea A=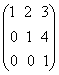 .Sa se calculeze B=
.Sa se calculeze B=![]() unde n
unde n![]() N*.
N*.
REZOLVARE: A=I+B sau 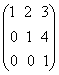 =
= +
+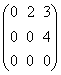 deci B=
deci B= => B2=
=> B2=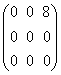 B3=0 B3=
B3=0 B3= deci Bn=0
deci Bn=0 ![]() n
n![]() 3 n
3 n![]() N si An=(I+B)n=C
N si An=(I+B)n=C![]() In+C
In+C![]() In-1B+C
In-1B+C![]() In-2B2+....+C
In-2B2+....+C![]() Bn= =
Bn= = +n
+n +
+![]()
 +...+
+...+
An=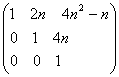
Cum ![]() =n;
=n; ![]() =
=![]() ;
; ![]() =
=![]() .Avem B=
.Avem B=![]() =
=
Observatie: A![]() Mn(C) se poate calcula An,n
Mn(C) se poate calcula An,n![]() N* si prin alta
metode,
N* si prin alta
metode,
ca: 1)prin inductie matematica
Exemplu: Fie A=![]() M2(Z) pentru a calcula An observam ca A2=
M2(Z) pentru a calcula An observam ca A2=![]() ,A3=
,A3=![]() cea ce ne face sa presupunem ca An=
cea ce ne face sa presupunem ca An=![]() ,
,![]() .
.
Demonstram aceasta propozitie folosind metoda inductiei matematice:
etapa de verificare n=1 => A=![]()
presupunem Ak=![]() si sa demonstram ca Ak+1=
si sa demonstram ca Ak+1=![]() ;
; ![]()
![]()
deci An=![]() ,
,![]() .
.
Se poate
calcula An, n![]() N *,si folosind sirurile recurente:
N *,si folosind sirurile recurente:
Exemplu: Fie matricea A=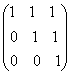 .Sa se calculeze An, n
.Sa se calculeze An, n![]() N.
N.
REZOLVARE: Notam An=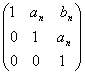 .Substituind pe n cu n+1 obtinem: An+1=
.Substituind pe n cu n+1 obtinem: An+1=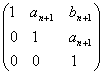 .
.
Pe de alta parte calculand An+1=An A avem
An+1= 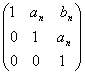
 =
=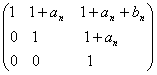 deci se obtin relatiile
deci se obtin relatiile ![]() =>an=n
si bn=
=>an=n
si bn=![]() si deci An=
si deci An=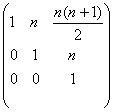 ,n
,n![]()
Fie H=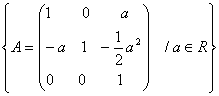
a)
Sa se arate ca (H,![]() ) este grup abelian(operatia "
) este grup abelian(operatia "![]() ",este operatia de [nmultire a matricilor).
",este operatia de [nmultire a matricilor).
b) Sa se arate ca (H,)este izomorf cu grupul aditiv al numerelor reale (R,+).
REZOLVARE: 1.Fie
Ax![]() H si Ay
H si Ay![]() H sa aratam ca operatia este bine definita
,sau ca (H,
H sa aratam ca operatia este bine definita
,sau ca (H, ![]() ) stabila:
) stabila:
dar Ax![]() Ay=
Ay=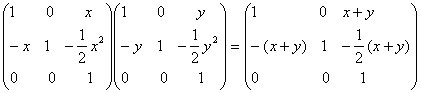 deci Ax
deci Ax![]() Ay=Ax+y
Ay=Ax+y![]() H pentru ca x
H pentru ca x![]() R,y
R,y![]() R si x+y
R si x+y![]() R.
R.
2.Asociativitatea : (Ax![]() Ay)Az=Ax(Ay
Ay)Az=Ax(Ay![]() Az;
Az;![]() Ax,Ay,Az
Ax,Ay,Az![]() H evident pentru ca A(x+y)+z=Ax+(y+z)
H evident pentru ca A(x+y)+z=Ax+(y+z)
3.Comutativitatea Ax![]() Ay=Ay
Ay=Ay![]() Ax ,
Ax , ![]() Ax,Ay
Ax,Ay![]() H evident pentru ca Ax+y=Ay+x
H evident pentru ca Ax+y=Ay+x
Elementul neutru ![]() AeAx=AxAe=A
dar Ax
AeAx=AxAe=A
dar Ax![]() Ae=Ax Ax+e=Ax x+e=x
=>e=0 deci Ae=A0=
Ae=Ax Ax+e=Ax x+e=x
=>e=0 deci Ae=A0=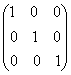
Simetricul: ![]() Ax
Ax![]() H,
H,![]() A
A![]()
![]() H astfel [ncat Ax A
H astfel [ncat Ax A![]() = A
= A![]() Ax=A0 dar
Ax=A0 dar
Ax A![]() =A0 =>A
=A0 =>A![]() =A0 =>x+x1=0 =>x1=-x => A
=A0 =>x+x1=0 =>x1=-x => A![]() =
=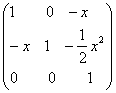
![]() H
H
Deci (H,![]() ) este grup abelian.
) este grup abelian.
c)
Se considera f:R H, x--->f(x)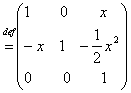
1)Se verifica f bijectiva
iar relatia f(x)f(y)=f(x+y) evident pentru ca f(x)=Ax, f(y)=Ay ,AxAy=Ax+y deci f(x)f(y)=AxAy=Ax+y=f(x+y).
Exercitii propuse:
1.Sa se determine
parametri ![]() astfel [ncat matricea
A sa verifice relatia A2-
astfel [ncat matricea
A sa verifice relatia A2-![]() A+
A+![]() I2=O2 unde O2=
I2=O2 unde O2=![]() si I2=
si I2=![]() .
.
2.Fie A=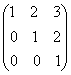 calculati An,
calculati An,
![]() .
.
3.Se considera multimea
de matrici G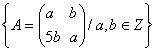 .Sa se demnstreze ca
G este parte stabila a lui M2(Z) [n raport cu adunarea ,respectiv
[nmultirea matricelor.
.Sa se demnstreze ca
G este parte stabila a lui M2(Z) [n raport cu adunarea ,respectiv
[nmultirea matricelor.
Sa se arate ca (G,+,![]() ) formeza o structura de inel comutativ fara divizori a lui
zero.
) formeza o structura de inel comutativ fara divizori a lui
zero.
DETERMINAN|I
Determinantul este un numar real atasat
unei matrice patratice;Exemplu:A= detA=
detA=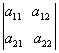 =a11a22-a12a21
=a11a22-a12a21
A= atunci det A=
atunci det A= care se calculeaza cu regula lui Sarrus sau a triunghiului.
care se calculeaza cu regula lui Sarrus sau a triunghiului.
Obs. Determinantii de ordin mai mare dec[t 3 se calculeza pe baza proprietatilor acestora.
Proprietati:
1.Daca A![]() Mn(C) atunci detA=detAt.
Mn(C) atunci detA=detAt.
2.Daca toate elementele unei linii(sau coloane) dintr-o matrice sunt nule,atunci determinantul matricii este nul.
3.Daca [ntr-o matrice schimbam doua linii(sau coloane) [ntre ele obtinem o matrice care are determinantul egal cu opusul determinantului matricei initiale.
4.Daca o matrice are doua linii(sau coloane)identice,atunci determinantul sau este nul.
5.Daca toate
elementele unei linii(sau coloane) ale unei matrici sunt [nmultite cu un numar ![]() ,obtinem o matrice al carei determinant este egal cu
,obtinem o matrice al carei determinant este egal cu ![]() [nmultit cu
determinantul matricei initiale.
[nmultit cu
determinantul matricei initiale.
6.Daca elementele unei linii(sau coloane) ale unei matrici sunt proportionale ,atunci determinantul matricei este nul.
7.Daca o linie(sau coloana)a unei matrici patratice este o combinatie
liniara cu celelalte linii (sau colone) atunci determinantul matricei este zero.
8.Daca la o linie(sau coloana) a matricei A adunam elementele altei linii (sau coloana) [nmultite cu acelasi numar,atunci aceasta matrice are acelasi determinant ca matricea A.
Calculul determinantilor: d= determinantului de
ordinul 3 se obtine suprimand linia i si coloana j,
determinantului de
ordinul 3 se obtine suprimand linia i si coloana j,![]()
![]() din determinantul d
din determinantul d![]() se numeste minusul elementului aij si se noteaza
dij iar
se numeste minusul elementului aij si se noteaza
dij iar ![]() =(-1)i+jdij se numeste complement
algebric al elementului aij [n determinantul d.
=(-1)i+jdij se numeste complement
algebric al elementului aij [n determinantul d.
Teorema: Fie
determinantul d=![]() atunci d=ai1
atunci d=ai1![]() i1+ai2
i1+ai2![]() i2+ai3
i2+ai3![]() i3+ai4
i3+ai4![]() i4 reprezinta dezvoltarea determinantului
d dupa linia i.
i4 reprezinta dezvoltarea determinantului
d dupa linia i.
Exemplu:1) Sa se
calculeze determinantul d=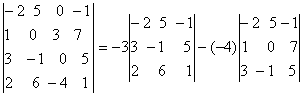 =(-3)*77+4* 67=-231+268=37
=(-3)*77+4* 67=-231+268=37
2)Determinantul Vanderman de ordin 3.
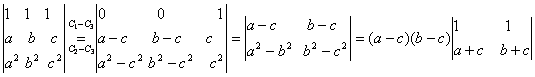 = =(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)=(a-b)(b-c)(c-a)
= =(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)=(a-b)(b-c)(c-a)
3.Sa se rezolve ecuatia:
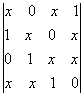 =5
=5
Rezolvare: 
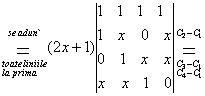
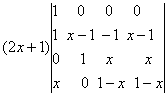 =
=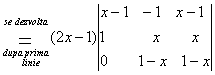 =
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Ecuatia
devine -4x3+2x2+1=5
sau 2x3-x2+2=0 se observa ca -1 este radacina,se aplica
schemalui Horner 2 -1 0 3 x1=-1 si
Ecuatia
devine -4x3+2x2+1=5
sau 2x3-x2+2=0 se observa ca -1 este radacina,se aplica
schemalui Horner 2 -1 0 3 x1=-1 si
2x2-3x+3=0 x23=![]() -1 2 -3 3 0
-1 2 -3 3 0
Definitie :Fie A Mmn(C) o matrice nenula.Spunem ca matricea A are rangul r si scriem rangA=r,daca A are un minor nenul de ordin r , iar toti minorii lui A de ordin mai mare decat r (daca exista)sunt nuli.
Exercitiu rezolvat: Fie matricea A= 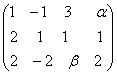 .Sa se calculeze
rangul matrice A.
.Sa se calculeze
rangul matrice A.
Rezolvare: Cum A![]() M34(R)
M34(R) ![]() minori de ordinul doi
d=
minori de ordinul doi
d=![]() 0 deci rang A
0 deci rang A![]() 2.Se calculaza minorii de ordinul trei care sunt C43=4
2.Se calculaza minorii de ordinul trei care sunt C43=4
d1=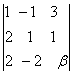 =3(
=3(![]() -6), d2=
-6), d2=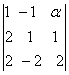 =3(2-2
=3(2-2![]() )sau doar pe cei obtinuti prin
bordarea lui d.
)sau doar pe cei obtinuti prin
bordarea lui d.
caz 1:d2=0
d3=0 adica ![]() =1,
=1, ![]() =6 => rangA=2
=6 => rangA=2
caz 2:d2![]() 0 sau d3
0 sau d3![]() 0 adica
0 adica ![]()
![]() 1 sau
1 sau ![]()
![]() 6 => rangA=3
6 => rangA=3
Matrici inversabile:
Definitie: O matrice patratica se numeste nesingulara daca determinantul sau este nenul.
Definitie:Fie o matrice patratica de ordin n.Se spune ca A este inversabila,daca exista o matrice B patratica de ordin n,astfel [ncat :
AB=BA=In; B se numeste inversa matricei A.
Teorema: A![]() Mn(C).matricea A este inversabila daca si numai
daca det A
Mn(C).matricea A este inversabila daca si numai
daca det A ![]() 0 sau este nensingulara si A-1=
0 sau este nensingulara si A-1=![]() A* unde A* se numeste matrice adjuncta formata din complementii
algebrici din matricea transpusa.
A* unde A* se numeste matrice adjuncta formata din complementii
algebrici din matricea transpusa.
Exemplu 1: Fie A=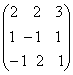 .Sa se arate ca este inversabila si [n caz afirmativ calculati A-1.
.Sa se arate ca este inversabila si [n caz afirmativ calculati A-1.
Rezolvare: d=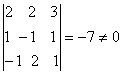 deci este inversabila si A-1=
deci este inversabila si A-1=![]() A* dar
A* dar
At=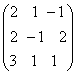 A11=+
A11=+![]() =-3, A12=-
=-3, A12=-![]() =4, etc... , A*=
=4, etc... , A*=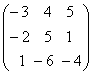 deci A-1=
deci A-1=![]() A* sau A-1=() verificarea:A A-1=A-1
A=I3 unde I3=
A* sau A-1=() verificarea:A A-1=A-1
A=I3 unde I3=
.Fie A=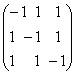 a)Sa se arate ca A
este inversabila si sa se calculeze A-1.
a)Sa se arate ca A
este inversabila si sa se calculeze A-1.
b)Determinati
X astfel [ncat A X=B unde B=![]() .
.
Rezolvare:
a)
A este
inversabila pentru ca det A=4 deci d![]() 0 deci A-1=
0 deci A-1=![]() A*.Se observa ca At=A.
A*.Se observa ca At=A.
avem A*=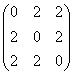 ,A-1=
,A-1=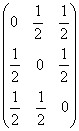 .
.
b)ecuatia AX=B
are solutia X=A-1B si prin calcul direct obtinem:X=
![]() => X=
=> X=![]() sau altfel AX=B
sau altfel AX=B 
![]() =
=![]()
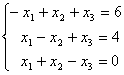 cu
cu ![]() =4.Prin regula lui cramer xi=
=4.Prin regula lui cramer xi=![]() =>
=> 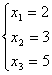
Exercitii de rezolvat:
Sa se determine matricea X care satisface
egalitatea X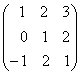 =
=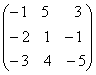
Indicatie: ecuatia este de forma XA=B si solutia care este unica are forma X=BA-1(a nu se uita ca [nmultirea matricelor nu este comutativa).
Se considera matricea X cu proprietatea X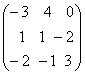 =
=![]()
Precizati tipul matricei x si apoi determinati aceasta matrice.
3)Se
considera matricea A=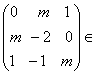 M3(C)
M3(C)
a)pentru ce valori complexe ale lui m matricea A este inversabila.
b)pentru m=2 sa se determine inversa matricei A.
4)Fie ecuatia x3-(2m-1)x2+(1+2m)x-m=0;
m![]() R.Sa se determine m astfel [ncat matricea: A=
R.Sa se determine m astfel [ncat matricea: A=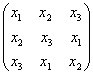 sa fie inversabila unde x1,x2,x3
sunt radacinile ecuatiei date.
sa fie inversabila unde x1,x2,x3
sunt radacinile ecuatiei date.
5)Se
considera multimea M=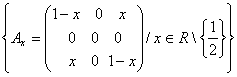 .Sa se demonstreze ca [nmultirea matricelor este lege de
compozitie interna pe M si ca (M,
.Sa se demonstreze ca [nmultirea matricelor este lege de
compozitie interna pe M si ca (M,![]() ) este grup abelian.
) este grup abelian.
6)Se
considera polinomul P(x)=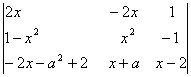 Sa se determine parametrul real a pentru care polinomul
admite radacina dubla [ntreaga.
Sa se determine parametrul real a pentru care polinomul
admite radacina dubla [ntreaga.
|