Metode de rezolvare a problemelor
Metoda figurativa
Metoda figurativa consta in reprezentarea grafica a datelor sau marimilor care apar in cazul unei probleme. Aceasta metoda are avantajul ca se intelege mai usor de catre scolar dependenta dintre marimile cunoscute si cele necunoscute ale problemei considerate.
In aplicarea acestei metode se pot folosi diferite elemente grafice sau combinatii de elemente grafice. Dintre acestea enumeram:
figuri geometrice: segmentul de dreapta (cel mai des folosit), triunghiul, dreptunghiul, patratul, cercul;
elemente grafice simple: puncte, linii, ovale, cerculete;
litere si combinatii de litere;
desene care reprezinta actiunea problemei.
In continuare vom da cateva exemple de probleme care pot fi rezolvate cu metoda figurativa.
Reprezentarea prin desen.
Problema:
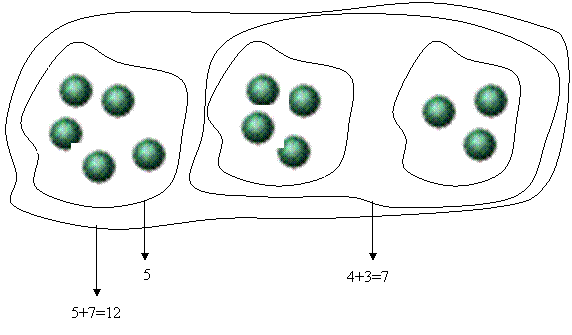
Ana are 5 mere. Fratele ei i-a mai dat 4 mere, iar sora ei inca 3 mere. Cate mere are Ana?
Rezolvare
 Fiind genul de
problema care se rezolva la clasa I, pentru a reprezenta marimile (in cazul
problemei considerate, merele), vom folosi desenul.
Fiind genul de
problema care se rezolva la clasa I, pentru a reprezenta marimile (in cazul
problemei considerate, merele), vom folosi desenul.
Elevii vor afla, mai intai, prin numarare, cate mere a primit in total Ana de la fratele si sora ei: 4+3=7.
Apoi vor afla cate mere are Ana in total:5+7=12.
Raspunsul problemei: 12 mere.
Aceasta problema putea fi facuta si direct, punand de prima data intrebarea din enuntul problemei: cate mere are Ana in total?
La aceasta intrebare elevii ar fi numarat toate merele desenate si ar fi ajuns la raspunsul: 5+4+3=12 mere.
Utilizarea figurilor geometrice plane.
Desi pot fi utilizate orice figuri geometrice plane (cercuri, patrate, dreptunghiuri etc.) cel mai folosit mod de reprezentare este cel ce foloseste segmentele de dreapta.
In acest caz gasim mai multe tipuri de probleme.
a. Aflarea a doua numere cand se cunosc suma si diferenta lor.
Problema
Suma a doua numere este 95. Sa se afle cele doua numere, stiind ca unul este cu 17 mai mare decat celalalt.
Rezolvare.
Pentru a rezolva aceasta problema vom reprezenta cele doua numere prin segmente de dreapta. Vom desena mai intai numarul mai mic, printr-un segment, apoi numarul mai mare. Stim ca acesta este cu 17 mai mare decat primul, deci il vom desena astfel: facem un segment egal cu cel care reprezinta primul numar, si ii vom adauga un segment suplimentar care va reprezenta cele 17 unitati ce reprezinta diferenta dintre numere.

Mai stim din problema ca cele doua numere adunate dau suma 95. Vom reprezenta acest lucru in felul urmator:

Pentru a determina cele doua numere, trebuie mai intai sa obtinem doua segmente la fel de mari. Acest lucru il putem face in doua moduri: prin adunare sau prin scadere.
a. Prin adunare
 Observam ca daca
numarului mic i-am aduna 17 unitati, atunci cele doua segmente obtinute ar fi
egale. Pentru a mentine insa egalitatea, adunand la segment 17 unitati trebuie
sa adunam aceeasi cantitate si la suma. Obtinem astfel:
Observam ca daca
numarului mic i-am aduna 17 unitati, atunci cele doua segmente obtinute ar fi
egale. Pentru a mentine insa egalitatea, adunand la segment 17 unitati trebuie
sa adunam aceeasi cantitate si la suma. Obtinem astfel:
Am obtinut astfel doua segmente egale care adunate dau 16216p1522q suma 112. Pentru a afla cat reprezinta un segment, vom face impartirea:
Acesta este insa segmentul ce reprezenta numarul mai mare, deci numarul mai mare are valoarea 56.
Cum numarul mai mic este cu 17 mai mic decat celalalt, vom afla valoarea acestuia prin scadere:
56-17=39 (numarul cel mic).
Am obtinut astfel valorile celor doua numere: 39 si 56.
b. Prin scadere.
Observam ca daca din numarul mare am scadea 17 unitati, atunci cele doua segmente obtinute ar fi egale. Pentru a mentine insa egalitatea, scazand din segment 17 unitati trebuie sa scadem aceeasi cantitate si din suma. Obtinem astfel:

Am obtinut astfel doua segmente egale care adunate dau 16216p1522q suma 78. Pentru a afla cat reprezinta un segment, vom face impartirea:
Acesta este insa segmentul ce reprezenta numarul mai mic, deci numarul mai mic are valoarea 39.
Cum numarul mai mare este cu 17 mai mare decat celalalt, vom afla valoarea acestuia prin adunare:
39+17=56 (numarul cel mare).
Am obtinut astfel valorile celor doua numere: 39 si 56
b. Aflarea a doua numere cand se cunosc suma si raportul lor.
Problema
Suma a doua numere este 560. Al doilea numar este de trei ori mai mare decat celalalt. Care sunt cele doua numere?
Rezolvare.
Pentru a rezolva aceasta problema vom reprezenta cele doua numere prin segmente de dreapta. Vom desena mai intai numarul mai mic (primul), printr-un segment, apoi numarul mai mare. Cum al doilea numar este de trei ori mai mare decat celalalt, rezulta ca pentru a il reprezenta, vom desena segmentul corespunzator primului numar de trei ori:

Cunoastem suma celor doua numere, deci desenul va fi:

Din desen se observa ca avem 4 segmente de aceeasi lungime care impreuna dau suma 560. Pentru a afla lungimea unui singur segment, este suficient sa impartim suma 560 la numarul de segmente egale (4):
560:4=140 - lungimea unui segment.
Tot din desen se vede insa ca segmentul cu lungimea 140 reprezinta chiar primul numar.
Pentru a afla cel de-al doilea numar, cum stim ca el este de 3 ori mai mare ca primul, va trebui sa facem inmultirea:
140*3=420 - valoarea celui de-al doilea numar.
c. Aflarea a doua numere cand se cunosc diferenta si raportul lor.
Problema
Tatal are de 4 ori mai multi ani decat fiul, adica cu 24 de ani mai mult. Cati ani are tatal? Cati ani are fiul?
Rezolvare.
Si de aceasta data vom reprezenta varstele tatului si fiului prin segmente de dreapta. Vom desena mai intai varsta cea mai mica - adica a fiului, iar a tatalui o vom desena, asa cum spune problema, de patru ori mai mare.

Stim insa ca tatal are cu 24 de ani mai mult decat fiul. Urmarind pe desen, observam ca diferenta dintre cele doua segmente este data de:
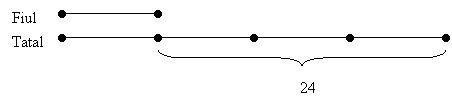
Cum toate segmentele desenate au aceeasi lungime, rezulta ca 24 reprezinta valoarea a trei segmente egale adunate. Valoarea unui singur segment va fi:
Cunoscand valoarea unui segment, rezulta ca am aflat varsta fiului:8 ani.
Varsta tatalui este de patru ori mai mare decat a fiului, deci:
8*4=32 ani are tatal.
Reprezentare schematica.
Problema
Intr-o curte sunt gaini si iepuri. Stiind ca in total sunt 11 capete si 34 de picioare, sa se afle cate gaini si cati iepuri sunt.
Rezolvare.
Cum in curte sunt 11 capete, inseamna ca sunt de fapt 11 animale, unele cu doua picioare (gainile) altele cu 4 picioare (iepurii).
Vom desena cele 11 animale prin 11 cerculete (ovale):

Trebuie in continuare sa distribuim cele 34 de picioare. Fiecare animale are cel putin cate doua picioare. Din acst motiv, vom desena cate doua picioare fiecarui animal.
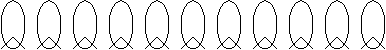
Am distribuit astfel 2x11=22 picioare din totalul de 34. Au mai ramas in plus 34-22=12 picioare.
Plusul de 12 picioare se datoreaza faptului ca unele animale (iepurii) nu au numai 2, ci patru picioare. Nu ne mai ramane decat sa distribuim pe desen cele doua picioare ramase, doua cate doua.

Dupa ce am distribuit restul de picioare, numaram cate animale cu 2 si cate cu 4 picioare avem. Obtinem:
6 animale cu patru picioare (iepuri)
5 animale cu doua picioare (gaini).
Metoda comparatiei
Metoda comparatiei este o metoda care ajuta la rezolvarea unui anumit tip de probleme. Acestea sunt problemele in care apar doua situatii distincte in care intervin aceleasi marimi, sau probleme in care apare o singura situatie, care este insa completata cu o relatie intre marimile ce apar in ea.
Problema
6 fete si 3 baieti aduna 33kg de zmeura, iar 6 fete si 7 baieti aduna 53kg de zmeura. Cate kg aduna o fata si cate un baiat?
In primul rand, la astfel de probleme trebuie sa scriem datele problemei sub o forma care sa ne fie de ajutor.
Vom scrie aceste date pe doua randuri, fiecare dintre cele doua randuri corespunzand uneia din cele doua situatii prezentate:
6 fete ...................... 3 baieti .................. 33kg zmeura
6 fete ...................... 7 baieti .................. 53kg. zmeura
Privind datele problemei astfel scrise, observam ca in ambele situatii numarul fetelor este acelasi. Diferenta care apare in ceea ce priveste cantitatea de zmeura culeasa este datorata numarului de baieti care in primul caz este mai mic iar in al doilea, mai mare.
Putem astfel concluziona ca diferenta de zmeura: 53kg-33kg=20kg zmeura este culeasa de 7-3=4 baieti.
Daca 4 baieti culeg 20 kg zmeura, atunci un baiat va culege de 4 ori mai putin:
20kg:4=5 kg zmeura culege un baiat.
Mai ramane de aflat cate kg de zmeura culege o fata.
Pentru aceasta alegem una dintre liniile de mai sus, de preferinta cea cu valorile cele mai mici (nu este insa obligatoriu!).
Alegem:
6 fete ...................... 3 baieti .................. 33kg zmeura
Aceasta linie ne spune ca 6 fete si 3 baieti culeg impreuna 33kg de zmeura. Stim insa ca un baiat culege 5kg. Astfel, din cele 33 kg, cei trei baieti culeg
5x3=15kg.
Raman restul de
33kg-15kg=18kg zmeura pe care le culeg cele 6 fete.
O fata va culege:
18kg:6=3kg zmeura (culege o fata.
Problema
4 saci cu grau si 3 saci cu porumb cantaresc 380kg, iar 5 saci cu grau si 6 saci cu porumb cantaresc 610kg. Cat cantereste un sac cu grau? Dar unul cu porumb.
Rezolvare
Vom proceda ca la problema anterioara si vom scrie datele problemei in mod convenabil:
4 saci grau ...................... 3 saci porumb ...................... 380kg
5 saci grau ...................... 6 saci porumb ...................... 610kg
Spre deosebire de problema precedenta, acum nici numarul sacilor de porumb nici cel al sacilor cu grau nu este acelasi in ambele situatii. Totusi, se poate observa ca numarul sacilor de porumb din a doua linie este dublu fata de numarul sacilor cu porumb din prima linie. Pentru a obtine un numar egal de saci de porumb este astfel suficient sa inmultim cu doi valorile de pe prima linie, in timp ce a doua linie va ramane nemodificata. Obtinem:
4 saci grau...................... 3 saci porumb ...................... 380kg x2
5 saci grau ...................... 6 saci porumb ...................... 610kg
adica
8 saci grau ...................... 6 saci porumb ...................... 760kg
5 saci grau ...................... 6 saci porumb ...................... 610kg
Cum numarul sacilor de porumb este de aceasta data acelasi in ambele situatii, vom proceda in continuare exact ca la problema precedenta.
Vom obtine ca diferenta de 760kg-610kg=150kg corespunde diferentei dintre numarul sacilor de grau: 8-5=3 saci de grau. Daca 3 saci de grau cantaresc 150kg, rezulta ca un sac va cantari:
150kg:3=50kg (cantareste un sac cu grau).
Alegem acum linia cu cele mai mici valori. Aceasta este:
4 saci grau ...................... 3 saci porumb ...................... 380kg
Cei 4 saci cu grau cantaresc 4x50kg=200kg, deci 3 saci cu porumb cantaresc 380kg-200kg=180kg.
Rezulta ca un sac cu porumb cantareste:
180kg:3=60kg (cantareste un sac cu porumb)
Problema
3kg de cartofi si 4kg de morcovi costa 64000lei. 2kg de cartofi si 5kg de morcovi costa 66000lei. Cat costa 1kg de cartofi? Dar unul de morcovi?
Rezolvare
Scriem datele problemei pe doua linii:
3kg cartofi ............ 4 kg morcovi ................. 64 000lei
2kg cartofi ............ 5kg morcovi .................. 66 000lei
Observam ca nu ne aflam in nici una din situatiile anterioare, adica nici una dintre cele doua marimi (cartofi sau morcovi) nu are aceeasi valoare in ambele situatii si nici una dintre valorile marimilor nu este proportionala cu valoarea din cealalta situatie.
In acest caz va trebui sa inmultim ambele linii cu anumite valori pentru a obtine fie acelasi numar de kg de cartofi fie de morcovi.
Daca dorim sa egalam numarul kilogramelor de cartofi, vedem ca in prima linie avem 3kg iar in cea de-a doua, 2kg. De aici deducem ca trebuie ca prima linie sa o inmultim cu 2 iar a doua cu 3, obtinand astfel in ambele cazuri 6kg cartofi:
3kg cartofi ............ 4 kg morcovi ................. 64 000lei x2
2kg cartofi ............ 5kg morcovi .................. 66 000lei x3
adica
6kg cartofi ............ 8 kg morcovi ................. 128 000lei
6kg cartofi ............ 15kg morcovi ................ 198 000lei
Mai departe procedam ca mai inainte.
Diferenta 198000-128000=70000lei corespunde celor 15kg-8kg=7kg morcovi care sunt in plus in a doua linie. Rezulta ca un kg de morcovi costa:
70000lei:7=10 000lei costa un kg de morcovi.
Alegem acum linia:
3kg cartofi ............ 4 kg morcovi ................. 64 000lei
Cele 4kg de morcovi costa impreuna 4kgx10000lei=40 000lei deci 3kg de cartofi vor costa 64 000-40 000=24 000 lei, de unde:
24 000: 4= 6 000 lei costa un kg de cartofi.
Metoda falsei ipoteze
Aceasta metoda se poate aplica unui mare numar de probleme, atat timp cat problema considerata contine date proportionale.
Asa cum indica si numele metodei, in aplicarea acesteia se porneste de la o presupunere (eronata) functie pe care o facem in raport cu una dintre marimile pe care dorim sa le determinam. Incercam sa rezolvam problema in de presupunerea facuta si vom obtine niste valori in plus sau in minus, datorate ipotezei considerate. Aceste valori le vom compara cu datele reale si apoi vom gasi cu cat "am gresit" in presupunere.
Pentru exemplificare vom da cateva exemple de probleme ce se pot rezolva cu aceasta metoda.
Problema
Intr-un bloc cu 30 de apartamente cu doua si trei camere sunt in total 70 de camere. Cate apartamente cu doua camere si cate cu trei camere sunt?
Rezolvare
In rezolvarea acestei probleme vom face o presupunere in legatura cu numarul de camere de fiecare tip care exista in bloc.
Putem, de exemplu, presupune, ca toate apartamentele ar avea exact 2 camere. Ce se intampla in acest caz?
Daca toate camerele ar avea 2 camere, ar insemna ca in total ar fi 30x2=60 camere (deoarece avem 30 apartamente).
Stim insa ca in total sunt 70 camere, deci cu 70-60=10 camere mai mult decat am obtinut in urma presupunerii facute.
De unde rezulta aceasta diferenta? Din faptul ca nu toate apartamentele au 2 camere, unele dintre ele avand cate trei. Va trebui sa distribuim acum cele 10 camere unora dintre apartamente.
Ne punem urmatoarea intrebare: cate camere trebuie sa mai adaugam unui apartament pentru a-l "transforma" din apartament cu doua camere in apartament cu trei camere?
3camere-2camere=1 camera.
Va trebui ca cele 10 camere sa le distribuim la 10:1=10 apartamente. Cele 10 apartamente vor fi apartamentele cu trei camere iar restul de 30-10=20 apartamente sunt apartamentele cu doua camere.
Rezultatul este astfel: 10 apartamente cu 3 camere si 20 apartamente cu doua camere.
Observatie
In problema de mai sus am presupun la inceput ca toate apartamentele au 3 camere. Am fi putut sa presupunem ca toate apartamentele au 3 camere. In acest caz am fi obtinut un numar de 30x3=90 de camere, rezultand o diferenta de 90-70=20 camere. Diferenta s-ar fi datorat faptului ca unele dintre apartamente au nu 3, ci numai 2 camere. Cum diferenta dintre numarul de camere intre cele doua tipuri de apartamente este 3-2=1 camera, rezulta ca cele 20 de camere pe care trebuie sa le eliminam vor corespunde unui numar de 20:1=20 apartamente. Rezulta ca in bloc sun 20 apartamente cu 2 camere si restul de 30-20=10 apartamente au trei camere.
Problema
75kg de miere s-au turnat in 12 bidoane, unele de 8kg, altele de 5kg. Cate bidoane de fiecare fel au fost folosite?
Rezolvare
Vom presupune ca s-au folosit numai bidoane de 5kg. In acest caz, ar insemna ca s-au turnat
12x5=60kg miere.
Stim insa ca au fost 75kg de miere, cu
75kg-60kg-15kg mai mult.
Diferenta de 15kg apare datorita faptului ca nu toate bidoanele au fost de 5kg, unele fiind de mai mari, mai exact de 8kg.
Diferenta dintre capacitatea celor doua tipuri de bidoane este de 8kg-5kg=3kg.
Va trebui astfel ca cele 15kg suplimentare sa le grupam in grupuri de 3kg, lucru necesar pentru "transformarea" bidoanelor de 5kg in bidoane de 8kg. Vom avea
15:3=5 grupuri de cate trei kilograme, de unde concluzionam ca avem 5 bidoane de 8kg.
Restul de 12-5=7 reprezinta numarul bidoanelor de 5kg.
Rezulta ca s-au folosit 7 bidoane de 5kg si 5 bidoane de 8kg.
Observatie
Problema putea fi rezolvata si pornind de la presupunerea ca toate bidoanele ar fi fost de 8kg.
Problema
Intr-un magazin au fost aduse 31 de bicilete, triciclete si masinute pentru copii. Numarul masinutelor este de trei ori mai mare decat cel al biciletelor. Stiind ca numarul total de roti este de 105, sa se determine cate biciclete, cate triciclete si cate masinute au fost aduse.
Rezolvare
Observam ca de aceasta data avem trei tipuri de obiecte: bicilete, tricilete si masinute. Problema poate parea mult mai dificila la o prima vedere. Trebuie, insa, ca din datele problemei sa transformam informatiile astfel incat problema sa semene cu cele rezolvate anterior.
In afara de numarul total de obiecte si de numarul de roti, se mai cunoaste o relatie: faptul ca numarul masinutelor este de trei ori mai mare decat cel al biciletelor. Ne vom folosi mai intai de aceasta informatie.
Din moment ce masinile sunt de trei ori mai numaroase decat biciletele, putem spune ca pentru fiecare bicicleta existenta avem si trei masini. Putem deci considera un grup de 1 bicicleta si trei masini ca fiind o jucarie cu 2+3x4=14roti (o bicicleta are 2 roti iar trei masinute vor avea 3x4=12 roti). In continuare vom analiza problema ca si cum am avea doua tipuri de obiecte: tricicletele si jucariile cu 14 roti.
Sa presupunem acum ca toate obiectele ar fi triciclete. In acest caz am obtine
31x3=93 roti.
Mai ramane astfel o diferenta de 105-93=12 roti, diferenta care se datoreaza faptului ca am considerat ca toate obiectele ar avea 3 roti, in timp ce unele au 14 roti. Va trebui acum sa "transformam" o parte din triciclete in jucarii cu 14 roti. Trebuie insa sa facem acest lucru fara a modifica numarul total al jucariilor. Daca, de exemplu, am adauga 9 roti unei triciclete, am obtine un grup cu 14 roti, dar nu s-ar pastra numarul de jucarii: dintr-o tricicleta am obtine o bicicleta si trei masinute!!!!
Este deci nevoie ca pentru transformare sa luam 4 triciclete la care sa le adaugam rotile necesare pentru a obtine din ele grupul de o bicicleta si trei masinute. Cate roti va trebui sa mai alocam pentru 4 triciclete ca sa facem transformarea?
In primul rand trebuie sa vedem cate roti ar avea 4 triciclete impreuna:
3x4=12 roti.
Pentru a transforma, observam ca este nevoie sa adaugam inca
14-12=2roti.
Cum diferenta de roti care mai trebuia alocata este de 12, inseamna ca putem transforma
12:2=6 grupuri de cate 4 triciclete in grupuri de 1 bicicleta si 3 masinute.
Rezulta ca am obtinut
in total 6 biciclete, 3x6=18 masinute si restul de
Metoda mersului invers
Asa cum spune si numele, aceasta metoda se foloseste in cazul in care rezolvarea problemei se face pornind de la sfarsit catre inceput.
In astfel de probleme necunoscutele apar in prima parte a calculelor iar partea finala a acestora este cunoscuta.
Problema
Triplam un numar natural si scadem din el 21. Rezultatul astfel obtinut il triplam din nou si scadem din el 4. Obtinem astfel numarul 311. Care este numarul considerat?
Rezolvare
Sa notam numarul considerat cu a. In prima etapa il triplam, deci vom obtine 3a. Din rezultat vom scadea 21, adica vom ajunge la
3a-21
Rezultatul obtinut il triplam din nou si scadem 4, adica
(3a-21)x3-4
Stim ca rezultatul este 311, deci
(3a-21)x3-4=311.
Am ajuns astfel la ecuatia care se regaseste in enunt, aceasta fiind:
(3a-21)x3-4=311
Pentru a rezolva acest exercitiu vom proceda in felul urmator:
in partea stanga avem o valoare din care am scazut 4. Pentru a "scapa" de acest 4, il vom trece in partea dreapta, cu semn schimbat (altfel spus, vom adauga 4 in ambele parti ale egalitatii). Obtinem:
(3a-21)x3=311+4 adica
(3a-21)x3=315
in partea stanga avem acum o valoare inmultita cu 3. Vom imparti ambele parti ale egalitatii la 3 si vom obtine:
3a-21 =315:3 adica
3a-21 =105
adunam acum 21 in ambele parti si avem 3a =126
putem acum sa aflam numarul a impartind in ambii membrii cu 3: a=42.
Am obtinut deci numarul cautat, a=42.
Problema
Un excursionist a parcurs in prima zi 1/7 din drumul pe care il avea de facut, a doua zi 4/6 din ce i-a ramas, a treia zi 3/8 din noul rest, iar a patra zi restul de 40km. Cati km a parcurs in fiecare zi?
Rezolvare
Pentru a rezolva o astfel de problema este mai simplu sa ne ajutam de reprezentarea grafica a drumului.
Reprezentam drumul pe care il are de parcurs excursionistul prin urmatorul segment
In prima zi a parcurs 1/7 din intregul drum, deci va trebui sa impartim drumul in 7 parti egale:
Si sa indicam partea din drum parcursa in prima zi (1/7):
|
|
1/7 (partea parcursa in prima zi
Pentru urmatoarele zile au mai ramas restul de 6/7 din drum, adica:
A doua zi a parcurs 4/6 din ce a ramas, adica:
|
|
![]()
4/6 din rest (partea parcursa a doua zi)
Drumul ramas este:
In a treia zi a parcurs 3/8 din noul rest. Pentru a vedea pe desen cat anume a parcurs in a treia zi, va trebui sa impartim segmentul ramas in 8 parti egale si sa consideram trei dintre ele:
|
|
3/8 din noul rest
(partea parcursa a treia zi)
Partea ramasa este:
Stim insa ca aceasta ultima parte reprezinta 40km. Pentru a determina lungimea drumului, vom parcurge cu ajutorul desenului drumul invers, pornind de la ultima zi inspre prima.
Ultima parte are 40km, deci:
40km
Dar aceasta este partea care mai ramasese dupa a treia zi, deci "urcand" in reprezentarea grafica, putem indica pe desen cei 40km:
|
|
|
3/8 din noul rest
40km
Urmarin pe acest desen, observam ca cei 40km reprezinta de fapt 5/8 din segment, adica 5/8 din partea ramasa dupa a doua zi.
Calculm o optime: 40km:5=8km, deci cele 8 optimi vor avea 8x8=64km.
Rezulta ca drumul ramas dupa a doua zi a fost de 64km, si vom reprezenta acest lucru pe desenul de mai sus:
|
|
![]()
![]()
4/6 din rest (partea parcursa a doua zi) 64km.
Cei 64km reprezinta acum 2/6 din drumul ramas de parcurs dupa prima zi. Rezulta ca drumul total parcurs dupa prima zi este 3x64km=192km (puteam si acum sa impartim intai 64km la 2 pentru a afla o sesime din segment si apoi sa inmultim cu 6 pentru a afla lungimea acestui segment).
Cu aceasta lungime "urcam" din nou in reprezentarea grafica si ajungem la prima zi:
|
|
![]()
1/7 (partea parcursa in prima zi 192km
Cei 192km reprezinta 6/7 din drumul total, deci o septime din acesta va fi 192km:6=32km, iar drumul total va fi de 7x32km=224km.
Observatie:
Acest tip de problema mai este cunoscut si sub numele de problema cu rest din rest, si este tipul de problema care se incadreaza cel mai bine in metoda drumului invers.
Regula de trei simpla
In problemele care se rezolva cu ajutorul regulii de trei simpla apar doua marimi proportionale. Cum marimile pot fi direct proportionale sau invers proportionale, rezulta ca putem avea doua cazuri atunci cand aplicam aceasta regula.
Doua marimi sunt direct proportionale daca pe masura ce una dintre ele creste, si cealalta va creste in aceeasi proportie, si invers proportionale daca pe masura ce una dintre ele creste, cealalta va scadea in aceeasi proportie.
Regula de trei simpla poate fi aplicata in doua variante: prin reducere la unitate sau prin proportii.Vom da exemple pentru fiecare din tipurile de probleme ce pot aparea si vom aplica fiecare din cele doua variante ale regulii.
Problema
10 caiete costa 22000lei.. Cat vor costa 3 caiete?
Rezolvare
Pentru inceput vom scrie datele problemei intr-o forma convenabila:
10 caiete ................. 22000lei
3 caiete ...................? lei
Mai intai, observam ca cele doua marimi: numarul de caiete si pretul sunt direct proportionale: daca numarul de caiete creste, va creste si pretul platit.
a. Vom rezolva mai intai problema prin reducere la unitate. In acest sens, vom dori mai intai sa aflam cat costa un caiet.
10 caiete ................. 22000lei
1 caiet ...................? lei
Cum 10 caiete costa 22000lei, rezulta ca un caiet va costa de 10 ori mai putin, adica 22000lei:10=2200 lei (costa un caiet).
Stiind acum cat costa un caiet, putem afla cat costa 3 caiete:
1 caiet ................. 2200lei
3 caiete ...................? lei
Daca un caiet costa 2200lei, 3 caiete vor costa de 3 ori mai mult, adica
2200lei x3=6600 lei (costa 3 caiete)
b. Vom rezolva acum problema prin metoda proportiilor.
10 caiete ................. 22000lei
3 caiete ..................... x lei
Marimile fiind direct proportionale, raportul dintre doua valori ale aceleiasi marimi este egal cu raportul dintre valorile corespunzatoare celeilalte marimi, adica:
![]() , deci
, deci ![]() lei (costa 3 caiete).
lei (costa 3 caiete).
Problema
10 muncitori termina un pod in 21 de zile. In cat timp ar termina podul o echipa formata din 15 muncitori?
Rezolvare
Daca ar lucra mai multi muncitori, ei ar termina lucrarea mai repede. Astfel, avand in vedere ca daca numarul de muncitori creste, timpul necesar scade, inseamna ca avem de-a face cu marimi invers proportionale.
a. Vom rezolva problema mai intai prin reducere la unitate.
10 muncitori ................. 21 zile
15 muncitori ................. ? zile
Ne punem intrebarea: in cate zile ar termina podul daca ar lucra un singur muncitor?
10 muncitori ................. 21 zile
1 muncitor ... ................. ? zile
1 muncitor ar termina podul de 10 ori mai lent decat 10 muncitori, adica
21zile x 10 =210 zile (ar lucra un muncitor pentru a termina podusl)
Revenim acum la intrebarea initiala, anume: in cat timp ar termina podul 15 muncitori?
1 muncitor ................. 210 zile
15 muncitori ................. ? zile
Daca ar lucra 15 muncitori, acestia ar termina podul de 15 ori mai repede, adica:
210zile:15=14 zile (ar lucra 15 muncitori pentru a termina podul)
b. Rezolvam acum problema prin metoda proportiilor:
10 muncitori ................. 21 zile
15 muncitori ................. x zile
Marimile ce apar in problema sunt invers proportionale. Raportul a doua valori ale aceleiasi marimi va fi egal cu inversul raportului valorilor corespunzatoare pentru cealalta marime:
![]() adica
adica ![]() zile (ar lucra 15 muncitori pentru a termina
podul).
zile (ar lucra 15 muncitori pentru a termina
podul).
Regula de trei compusa
Este asemanatoare cu regula de trei simpla, cu deosebirea ca de aceasta data avem trei marimi, nu doar doua.
Problema
20 vaci consuma 2550kg furaj in 15zile. In cate zile vor consuma 18 vaci 4590kg furaj?
Rezolvare
Vom scrie datele problemei in mod convenabil:
20vaci .................. 2550kg furaj .......................... 15 zile
18 vaci ................. 4590kg furaj .......................... ? zile
Va trebui de aceasta data sa reducem la unitate doua dintre cel trei marimi care apar. Reducem mai intai numarul vacilor
20vaci .................. 2550kg furaj .......................... 15 zile
1 vaca ................... ? kg furaj .............................. 15 zile
Daca timpul este acelasi, atunci 1 vaca va consuma de 20 de ori mai putin decat 20 vaci:
![]() kg furaj (consuma o vaca in 15 zile).
kg furaj (consuma o vaca in 15 zile).
Vom afla acum cat consuma o vaca intr-o singura zi (va consuma de 15 ori mai putin):
![]() kg furaj (consuma o
vaca intr-o zi).
kg furaj (consuma o
vaca intr-o zi).
Stim acum ca:
1 vaca ......................... ![]() kg furaj
...................1 zi
kg furaj
...................1 zi
Revenim la intrebarea problemei: in cate zile vor consuma 18 vaci 4590kg?
Vom afla mai intai cat consuma 18 vaci intr-o zi:
![]() kg furaj.
kg furaj.
Deci 18 vaci consuma intr-0 zi 153kg furaj. Pentru a afla in cate zile vor consuma ele 4590kg, ne mai ramane sa facem impartirea: 4590kg:153kg=30 zile.
Raspunsul problemei este: 15 zile.
Observatie
In cazul regulii de trei compusa consideram ca este mai indicat sa se foloseasca reducerea la unitate, deoarece este mai usor de inteles.
Datorita faptului ca in problemele de acest tip apar trei marimi, este posibil ca una dintre ele sa fie direct proportionala cu celelalte doua sau este posibil sa fie direct proportionala cu una si invers proportionala cu cealalta, motiv pentru care scrierea proportiilor, in cazul in care acestea nu au fost foarte bine intelese de catre elev, va fi foarte dificila.
Pentru problema de mai sus, am avea, in cazul metodei proportiilor:
20vaci .................. 2550kg furaj .......................... 15 zile
18 vaci ................. 4590kg furaj .......................... x zile
de unde ![]() adica x=30
zile
adica x=30
zile
Probleme de miscare
Problemele de miscare sunt acele probleme in care avem de-a face cu miscarea unor mobile.
Miscarea rectilinie si uniforma este definita de legea de miscare:
![]() sau
sau ![]() .
.
Putem, in principiu, sa intalnim doua tipuri de probleme:
mobile care merg in acelasi sens (probleme de urmarire);
mobile care merg in sens contrar (probleme de intalnire).
Mobile care merg in acelasi sens
Problema
Un caine fuge dupa un iepure care este la 140m de el. Iepurele fuge cu 370m/minut, iar cainele cu 405m/minut. Dupa cat timp este iepurele prins de caine?
Rezolvare
La inceput, distanta dintre caine si iepure este de 140m. Cum viteza cainelui este de 405m/minut iar a iepurelui de 370m/minut, inseamna ca intr-un minut cainele se apropie de iepure cu 405-370=35m.
Daca intr-un minut cainele recupereaza 35m din distanta, in cat timp va recupera cei 140m?
140:35=4 minute.
Problema
Un tren circula de la Bucuresti spre
Rezolvare
Vom afla mai intai ce distanta parcursese primul tren in momentul in care a pornit cel de-al doilea. Cum acesta merge cu 56km/h, in trei ore a facut:
56km x3=168km.
Deci cel de-al doilea tren va trebui sa recupereze o distanta de 168km.
Intr-o ora, distanta dintre cele doua trenuri se micsoreaza cu
70km-56km=14km.
Pentru a recupera 168km va fi deci nevoie de:
168:14=12 ore.
In concluzie, al doilea tren il va ajunge pe primul dupa 12 ore de la plecarea sa.
Mobile care merg in sens contrar
Problema
Doi calatori pornesc unul spre altul din doua localitati, unul cu 4km/h, celalalt cu 5km/h. dupa cat timp se vor intalni, stiind ca distanta dintre localitati este de 18km?
Rezolvare
Vom calcula mai intai cu cat se micsoreza distanta intr-o ora. Avand in vedere ca cei doi merg unul spre celalalt, inseamna ca distanta dintre ei se va micsora cu 4+5=9km in interval de o ora.
Dar distanta este de 18km, deci de 2 ori mai mare decat cei 9km. Rezulta ca cei doi se vor intalni in 18:9=2ore de la pornire.
Problema
Un motociclist a pornit din localitatea A spre localitatea B cu 40km/h. Altul a pornit din B spre A cu 38km/h. Cei doi se intalnesc dupa 4 ore. Ce distanta este intre cele doua localitati?
Rezolvare
Mergand unul spre altul, cei doi se apropie in fiecare ora cu 40+38=78km. Daca intr-o ora se apropie cu 78km, atunci in 4 ore se vor apropia cu 78x4=312km. Rezulta ca distanta dintre cele doua orase este de 312km.
Probleme propuse
Ioana are o pisica si un catel. Stiind ca pisica are de doua ori varsta catelului si ca impreuna au 6 ani, sa se determine varsta celor doua animale.
Laura si Iulia au impreuna 24 de creioane colorate. Stiind ca Iulia are de trei ori mai putine creoiane decat Laura, sa se determine cate creioane are fiecare.
Elevii claselor A si au mers impreuna la cules de cirese. Elevii de la B au cules de 2 ori mai multe ladite decat elevii de la clasa A, adica au cules cu 6 ladite mai mult. Cate ladite de cirese au cules elevii de la A si elevii de la B ?
Intr-o curte se gasesc pui de gaina si pui de rata, in total 36 de pui. Stiind ca puii de gaina sunt cu 10 mai multi decat cei de rata, sa se afle cati pui de gaina si cati pui de rata sunt.
Suma a doua numere este 7 iar diferenta dintre ele este 3. Care sunt cele doua numere ?
Diferenta dintre doua numere est 12 iar raportul lor este 2. Care sunt cele doua numere ?
Alina a cumparat 3 caiete si a platit 57 000 lei. Cat ar fi platit daca ar fi cumparat 5 caiete ?
Mama a facut doua tavi de placinta cu mere si a obtinut 40 de bucati. Cate tavi ar fi trebuit sa faca pentru a obtine 60 bucati de placinta cu mere ?
Un muncitor termina o lucrare in 10 zile, lucrand cate 4 ore pe zi. In cate zile ar termina lucrarea daca ar munci 5 ore pe zi ?
Intr-un bloc sunt 36 de apartamente cu doua si trei camere. Stiind ca in total sunt 90 de camere, sa se afle cate apartamente de fiecare fel sunt.
Ionut are 14 de caiete, unele cu 48 de file si altele cu 100 de file. Stiind ca in total sunt 880 de file, sa se afle cate caiete de fiecare fel are Ionut.
Doua kilograme de mere si trei kilograme de prune costa 90 000lei. Trei kilograme de mere si doua de prune costa 85 000lei. Cat costa un kilogram de mere ? Dar unul de prune ?
Daca inmultim un numar cu 3 si altul cu 4 obtinem suma 92. Daca inmultim primul numar cu 4 si pe al doilea cu 3, obtinem suma 111. Care sunt cele doua numere ?
Un elev cheltuieste o sesime din suma pe care o are pe prajituri, doua cincimi din ce a mai ramas, pe timbre, un sfert din restul de bani pe suc si i-au mai ramas 90 000lei. Ce suma a avut initial ?
M-am gandit la un numar. Am adunat la acest numar trei. Rezultatul l-am inmultit cu 5 si am scazut apoi 20. Noul rezultat l-am impartit la 2 si am obtinut, in final, 20. La ce numar m-am gandit?
Un biciclist merge cu o viteza de 20km/ora. El porneste dintr-un punct A o jumatate de ora, alt biciclist porneste pe acelasi drum, cu o viteza de 24km/ora. Cei doi ajung in acelasi moment in punctul B. Dupa cat timp l-a prins din urma al doilea biciclist pe primul ? Care este distanta dintre A si B ?
Un vapor pleaca din portul A spre portul B cu viteza de 30km/ora. Alt vapor pleaca din B spre A cu 40km/ora. Stiind ca distanta dintre cele doua porturi este de 240km, sa se afle dupa cat timp se intalnesc cele doua vapoare. La ce distanta de portul A se vor intalni ? Dar de portul B ?
|