Piramida
Un poliedru cu una din fete poligon cu n laturi si celelalte fete triunghiuri care au in comun un varf se numeste piramida.
Poligonul cu n laturi se numeste baza piramidei , iar celelalte fete care sunt triunghiuri se numesc fetele laterale ale piramidei.
Laturile fetelor piramidei se numesc muchii.Muchiile care apartin bazei le numim muchiile bazei , iar celelalte muchii se numesc muchiile laterale ale piramidei.Varful comun al tuturor triunghiurilor se numeste varful piramidei.Denumirea piramidei se face dupa poligonul de baza (piramida triunghulara daca baza este triunghi , piramida patrulatera daca baza este patrulater , etc.)
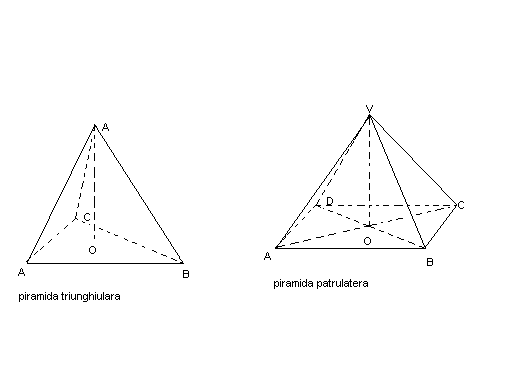
Inaltimea piramidei este segmentul dus din varful piramidei perpendicular pe planul bazei ([VO] - in figura)(segmentul determinat de varful piramidei si de piciorul perpendicularei din varf pe baza).Tot inaltime a piramidei vom numi si lungimea acestui segment.
O piramida se numeste regulata daca baza ei este un poligon regulat si proiectia ortogonala a varfului pe planul bazei coincide cu centrul poligonului bazei.Toate muchiile laterale ale piramidei sunt egale ; toate fetele laterale sunt triunghiuri isoscele congruente.Inaltimea unei fete laterale a unei piramide regulate dusa din varf se numeste apotema piramidei.O piramida triunghiulara (sau tetraedru) este o piramida care are baza un triunghi.Tetraedru se numeste regulat daca toate muchiile sunt egale.
Aria laterala (Sl) a unei piramide este egala
cu suma ariilor tuturor fetelor laterale (daca piramida este regulata , atunci 
,unde P este perimetrul bazei , iar a - apotema piramidei).
Aria totala ( a piramidei este egala cu : St = Sl +Sb , unde Sb este aria bazei.
Volumul
unei piramide este dat
de formula : 
, unde Sb este aria bazei , iar h - inaltimea
piramidei.
Trunchiul de piramida
Un poliedru ale carui varfuri sunt varfurile bazei unei piramide si varfurile sectiunii cu un plan paralel cu planul bazeiunei piramide se numeste trunchi de piramida.
Bazele unui trunchi de piramida sunt doua poligoane omotetice (ABCD , A'B'C'D' in figura)
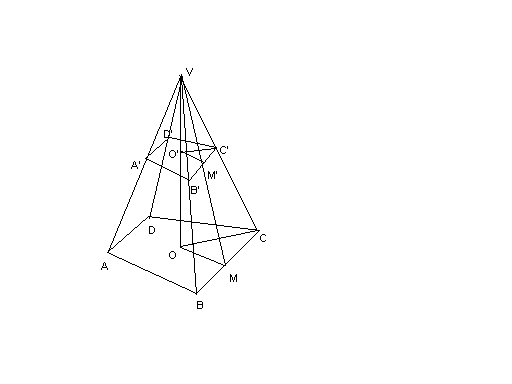
Centrul de omotetie este varful piramidei.Segmentul din perpendiculara dusa din varful piramidei pe planul bazei cuprins intre cele doua baze ([OO'] in figura) se numeste inaltimea trunchiului de piramida (altfel aceasta este distanta intre planele bazelor).Fetele laterale ale unui trunchi de piramida sunt trapeze.Trunchiul de piramida se numeste regulat daca provine dintr-o piramida regulata.Fetele laterale ale unui trunchi de piramida regulat sunt trapeze isoscele congruente.Inaltimea unui astfel de trapez se numeste apotema trunchiului de piramida regulat.
Aria laterala (Sl) a trunchiului de
piramida este egala cu suma ariilor fetelor laterale (daca trunchiul de
piramida este regulat , atunci 
, unde P , p sunt
perimetrele bazelor , iar a este apotema trunchiului).
Aria totala (St) a trunchiului de piramida este egala cu St = S +s + Sl , unde S , s sunt ariile bazelor.
Volumul trunchiului de piramida este dat de formula
: 
, unde h este
inaltimea trunchiului , iar S , s sunt
ariile bazelor.
Pentru piramidele VA'B'C'D' , VABCD sunt utile asemanarile :
1)
2)
De asemenea , sunt utile rapoartele
1)
, unde s = SA'B'C'D' , S = SABCD.(raportul
ariilor celor doua piramide este egal cu patratul raportulului inaltimilor
celor doua piramide)
2)
.(raportul volumelor celor doua piramide este egal cu cubul raportului
inaltimilor celor doua piramide)
|
