Polinoame

Polinoame

XIV.1. Forma algebricã a unui polinom

f C[x] este f = a₀Xⁿ + a₁X^n-1 + a₂X^n-2 + . + a_n, unde n este gradul, a₀ - coeficientul dominant, a_n - termenul liber.

Functia polinomialã asociatã lui f C[x] este :C C (a) = f(a) "a C; f(a) fiind valoarea polinomului f în a.

Teorema împãrtirii cu rest: "f,g C[x], g 0 existã polinoamele u 818j924i nice q,r C[x] astfel încât f = gq + r, grad r < grad g.

Împãrtirea unui polinom cu X-a: Restul împãrtirii polinomului f C[x], f 0 la X-a este f(a).

Schema lui Horner: ne ajutã sã aflãm câtul q = b₀X^n-1 + b₁X^n-2 + . + b_n-1 al împãrtirii polinomului f = a₀Xⁿ + a₁X^n-1 + a₂X^n-2 + . + a_n la binomul X-a; precum si restul acestei împãrtiri r = f(a);

XIV.2. Divizibilitatea polinoamelor

Definitia XIV.2.1. Fie f,g C[x], spunem cã g divide pe f si notãm g f dacã q C[x] astfel încât f=gq.

Proprietãti:

a f, "a C*, "f C[x];

g f si f 0 r = 0;

g f si f 0 grad f grad g;

a C* af f;

f f (refelexivitate);

f g si g h f h (tranzitivitate);

f g si g f a C* cu f = ag (f,g sunt asociate în divizibilitate).

Definitia XIV.2.2. Un polinom d se numeste cel mai mare divizor comun (c.m.m.d.c.) al polinoamelor f si g dacã: 1) d f si d g.

2) d' f si d' g d' d si notãm d=(f,g)

Definitia XIV.2.3. Dacã d=1 atunci f si g se numesc prime între ele.

Definitia XIV.2.4. Un polinom m se numeste cel mai mic multiplu comun (c.m.m.m.c.) al polinoamelor f si g dacã: 1) f m si g m.

2) f m' si g m' m m'

Teoremã. Dacã d=(f,g) atunci m =

XIV.3. Rãdãcinile polinoamelor

Definitia XIV.3.1. Numãrul a C se numeste rãdãcinã a polinomului f dacã si numai dacã (a) = 0.

Teorema lui Bezout: Numãrul a C este rãdãcinã a polinomului f 0 (X-a) f.

Definitia XIV.3.2. Numãrul a se numeste rãdãcinã multiplã de ordinul p a polinomului f 0 dacã si numai dacã (X-a) f iar (X-a)^p+1 nu-l divide pe f.

Teoremã: Dacã f C[x] este un polinom de gradul n si x₁,x₂,x₃,.,x_n sunt rãdãcinile lui cu ordinele de multiplicitate m₁,m₂,m₃,.,m_n atunci unde a₀ este coeficientul dominant al lui f, iar m₁ + m₂ + . + m_n = grad f.

XIV.4. Ecuatii algebrice

Definitia XIV.4.1. O ecuatie de forma f(x) = 0 unde f 0 este un polinom, se numeste ecuatie algebricã.

Teorema lui Abel-Ruffini: Ecuatiile algebrice de grad mai mare decât patru nu se pot rezolva prin radicali.

Teorema lui D'Alambert-Gauss: Orice ecuatie algebricã de grad mai mare sau egal cu unu, are cel putin o rãdãcinã (complexã).

Formulele lui Viete: Dacã numerele x₁,x₂,.,x_n sunt rãdãcinile polinomului f C[x], f = a₀Xⁿ + a₁X^n-1 + .+ a_n, a₀ 0 atunci:

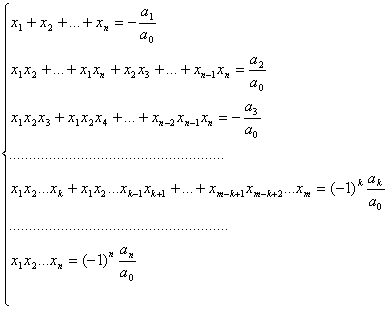
XIV.5. Polinoame cu coeficienti din R, Q, Z

Teoremã: Dacã f R[x] admite pe a = a + ib, b 0 ca rãdãcinã atunci el admite ca rãdãcinã si pe a = a - ib, iar a si a au acelasi ordin, de mutiplicitate.

Teoremã: Dacã un polinom f Q[x] admite pe a = a + b (a,b Q, b 0, d R\Q) ca rãdãcinã, atunci el admite si pe = a - b, iar a si a au acelasi ordin, de mutiplicitate.

Teoremã: Dacã un polinom f Z[x], grad f 1, admite o rãdãcinã a = Q, (p,q) = 1 atunci p a_n si q a₀.

În particular dacã f Z[x] are rãdãcina a=p Z atunci p a_n.