Polinomul Taylor asociat unei functii
5.1 Consideram functia ![]() si
si ![]() ,
oarecare, dar fixat. Presupunem ca functia
,
oarecare, dar fixat. Presupunem ca functia ![]() este
de clasa
este
de clasa ![]() intr-o vecinatate
intr-o vecinatate ![]() .
Atunci polinomul (functia polinomiala)
.
Atunci polinomul (functia polinomiala)
![]() ,
, ![]() . (1)
. (1)
se
numeste polinomul ![]() asociat functiei
asociat functiei ![]() in
punctul
in
punctul ![]() .
.
De exemplu, daca ![]() este un polinom de gradul
este un polinom de gradul ![]() si
si ![]() este functia polinomiala asociata, atunci polinomul Taylor asociat functiei
este functia polinomiala asociata, atunci polinomul Taylor asociat functiei ![]() are gradul
are gradul ![]() si reprezinta dezvoltarea functiei
si reprezinta dezvoltarea functiei ![]() dupa puterile lui
dupa puterile lui ![]() .
Avem
.
Avem
![]() .
(2)
.
(2)
Vom observa ca ![]() si
si ![]() .
.
Formula lui Taylor in care dezvoltarea se face dupa
puterile lui ![]() (
(![]() ),
adica are loc reprezentarea
),
adica are loc reprezentarea
![]() ,
(3)
,
(3)
este numita formula lui MacLaurin .
In particular, consideram polinomul ![]() .
Se cere sa se dezvolte dupa puterile lui
.
Se cere sa se dezvolte dupa puterile lui ![]() .
Fie
.
Fie ![]() ,
,
![]() ,
functia polinomiala asociata lui
,
functia polinomiala asociata lui ![]() .
Avem
.
Avem
![]()
![]() ;
;
![]()
![]()
![]()
Polinomul Taylor de gradul al treilea asociat functiei
polinomiale ![]() are forma
are forma
![]() .
(4)
.
(4)
Exercitii
Fie ![]() .
Sa se dezvolte dupa puterile lui
.
Sa se dezvolte dupa puterile lui ![]() .
.
Sa se scrie polinomul ![]() ,
in punctul
,
in punctul ![]() .
.
Sa se scrie polinomul 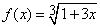 ,
in
,
in ![]() .
.
Fie ![]() .
Sa se scrie polinomul
.
Sa se scrie polinomul ![]() asociat functiei
asociat functiei ![]() in
in ![]() .
.
Sa se scrie
polinomul ![]() asociat functiei
asociat functiei ![]() ,
in punctul
,
in punctul ![]() .
.
Sa se calculeze ![]() si
si ![]() stiind ca
stiind ca ![]() este functie polinomiala de gradul al patrulea
determinata de conditiile:
este functie polinomiala de gradul al patrulea
determinata de conditiile:![]()
![]() ;
;
![]() ;
;
![]() si
si ![]() .
.
5.2. Formula
lui Taylor pentru functii de o variabila reala. Fie ![]() un interval inchis, nedegenerat din
un interval inchis, nedegenerat din ![]() si functia
si functia ![]() care verifica conditiile:
care verifica conditiile:
1). ![]() (exista derivatele pana la ordinul
(exista derivatele pana la ordinul ![]() inclusiv si acestea 747b16h sunt functii continue pe
inclusiv si acestea 747b16h sunt functii continue pe ![]() );
);
exista ![]() (derivata de ordinul
(derivata de ordinul ![]() a lui
a lui ![]() ),
finita sau infinita, in orice punct din
),
finita sau infinita, in orice punct din ![]() ;
;
Atunci exista ![]() astfel incat
astfel incat
![]() , (5)
, (5)
unde
![]() reprezinta restul care se obtine, in punctul
reprezinta restul care se obtine, in punctul ![]() ,
cand inlocuim valoarea
,
cand inlocuim valoarea ![]() cu valoarea
cu valoarea ![]() a polinomului
a polinomului ![]() asociat lui
asociat lui ![]() .
.
Mai mult, restul poate fi scris sub una din formele:
a). restul sub forma lui Lagrange,
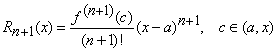 . (6)
. (6)
b). restul sub forma lui Cauchy,
![]() (7)
(7)
c). restul sub forma integrala,
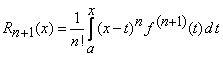 . (8)
. (8)
Demonstratie. Alegem restul sub forma ![]() ,
unde
,
unde ![]() este o constanta care depinde de alegerea lui
este o constanta care depinde de alegerea lui ![]() ,
iar
,
iar ![]() oarecare. Atunci problema se reduce la
determinarea constantei
oarecare. Atunci problema se reduce la
determinarea constantei ![]() a.i.
a.i.
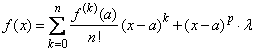 .
. ![]()
Consideram functia ![]() ,
definita pentru orice
,
definita pentru orice ![]() prin relatia
prin relatia
![]() .
.
Vom observa ca functia ![]() este continua pe
este continua pe ![]() deoarece functia initiala
deoarece functia initiala ![]() a fost presupusa de clasa
a fost presupusa de clasa ![]() pe
pe ![]() .
In plus, pentru
.
In plus, pentru ![]() din formula (
din formula (![]() )
obtinem
)
obtinem ![]() si pentru
si pentru ![]() deducem
deducem ![]() .
Functia
.
Functia ![]() este derivabila pe intervalul deschis
este derivabila pe intervalul deschis ![]() deoarece
deoarece ![]() a fost presupusa de clasa
a fost presupusa de clasa ![]() pe
pe
![]() .
In consecinta, functia
.
In consecinta, functia ![]() satisface conditiile teoremei lui Rolle pe
intervalul
satisface conditiile teoremei lui Rolle pe
intervalul ![]() .
Asadar, exista un punct
.
Asadar, exista un punct ![]() ,
a.i.
,
a.i. ![]() .
Alegem
.
Alegem ![]() cu
cu
![]() .
.
Avem
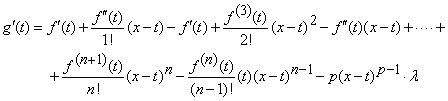
Dupa reducerea termenilor asemenea, rezulta
![]()
Deoarece ![]() ,
din ultima relatie, pentru
,
din ultima relatie, pentru ![]() ,
obtinem
,
obtinem
![]()
Deci, 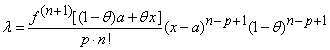 si atunci gasim urmatoarea expresie a restului
si atunci gasim urmatoarea expresie a restului
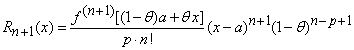 , cu
, cu ![]() . (9)
. (9)
Vom observa ca restul obtinut depinde de ![]() ,
unde
,
unde ![]() este un numar natural oarecare.
este un numar natural oarecare.
Daca alegem ![]() atunci, din ultima relatie, obtinem restul sub forma lui Lagrange (6), iar
pentru
atunci, din ultima relatie, obtinem restul sub forma lui Lagrange (6), iar
pentru ![]() obtinem restul
sub forma lui Cauchy (7).
obtinem restul
sub forma lui Cauchy (7).
5.3. Observatie.
Presupunand ca ![]() ,
atunci restul sub forma lui Lagrange devine
,
atunci restul sub forma lui Lagrange devine
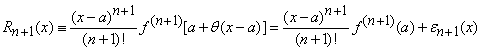
unde
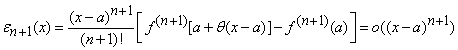 , cand
, cand ![]() .
.
Aici
am folosit faptul ca ![]() este functie continua pe
este functie continua pe ![]() si atunci
si atunci
![]() , cand
, cand ![]() .
.
In consecinta, daca ![]() atunci
atunci
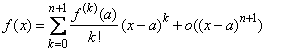 ,
cand
,
cand ![]() . (10)
. (10)
Formula (10) este cunoscuta sub numele
de formula lui Taylor corespunzatoare functiei
![]() in
punctul
in
punctul ![]() cu restul sub forma lui Peano .
cu restul sub forma lui Peano .
In continuare vom arata ca restul formulei lui Taylor poate fi scris sub forma integrala (8), adica are loc formula
 .
. ![]()
Pentra aceasta folosim inductia matematica dupa ![]() natural.
natural.
Pentru ![]() putem scrie relatia
putem scrie relatia ![]() , care evident, arata ca formula lui Taylor este
adevarata cand
, care evident, arata ca formula lui Taylor este
adevarata cand ![]() .
.
Presupunem ca formula ![]() este
adevarata pentru
este
adevarata pentru ![]() ,
atunci putem scrie
,
atunci putem scrie
 .
.
Integrand prin parti expresia restului, obtinem
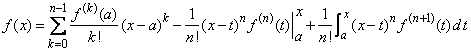
Asadar, avem
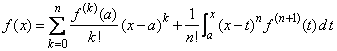 ,
,
de unde deducem ca
formula ramane adevarata si pentru pasul ![]() ,
deci relatia
,
deci relatia ![]() este adevarata pentru orice
este adevarata pentru orice ![]() .
.
5.4.
Observatie. Formula lui Taylor ramane
adevarata daca ![]() ,
,
![]() un interval nedegenerat si
un interval nedegenerat si ![]() este de
este de ![]() derivabila
intr-un punct
derivabila
intr-un punct ![]() deoarece prin aceasta conditie intelegem ca
deoarece prin aceasta conditie intelegem ca ![]() este de
este de ![]() derivabila
intr-o vecinatate
derivabila
intr-o vecinatate ![]() a punctului
a punctului ![]() si
si ![]() si exista derivata de ordinul
si exista derivata de ordinul ![]() a lui
a lui ![]() in
in ![]() .
.
5.5. Observatie. Formula lui Taylor cu restul sub forma integrala are numeroase aplicatii. De exemplu, in cazul functiilor suficient de netede, aceasta formula serveste la evaluarea restului in formulele de cuadratura numerica (integrare numerica).
5.6. Aplicatii ale formulei lui Taylor la dezvoltarea unor functii elementare.
Fie ![]() .
Deoarece
.
Deoarece ![]() putem scrie
putem scrie
![]()
unde ![]() .
.
In consecinta, formula lui Taylor scrisa dupa puterile
lui ![]() (dezvoltarea are loc in jurul punctului
(dezvoltarea are loc in jurul punctului ![]() ),
corespunzatoare functiei
),
corespunzatoare functiei ![]() ,
cu restul lui Lagrange se scrie
,
cu restul lui Lagrange se scrie
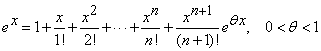 , (11)
, (11)
unde, restul sub forma lui Lagrange are expresia
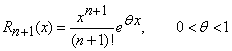 . (12)
. (12)
Mai mult, au loc extimarile:
a) pentru orice ![]() ,
avem
,
avem 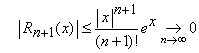 .
.
b) pentru orice ![]() ,
avem
,
avem 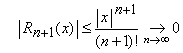 .
.
Fie ![]() ,
,
![]() .
In acest caz
.
In acest caz ![]() si avem
si avem
![]() ,
, ![]()
In consecinta, formula lui Taylor dupa puterile lui ![]() (in polinomul Taylor apar numai puterile pare
ale lui
(in polinomul Taylor apar numai puterile pare
ale lui ![]() )
poate fi scrisa astfel
)
poate fi scrisa astfel
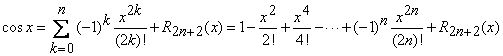 , (13)
, (13)
unde, restul sub forma lui Lagrange are expresia
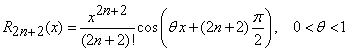 . (14)
. (14)
Putem scrie extimarea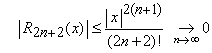 .
.
Fie ![]() ,
,
![]() .
Atunci
.
Atunci ![]() si avem
si avem
![]() ,
, ![]()
Atunci putem scrie formula lui Taylor dupa puterile lui
![]() (in dezvoltare apar numai puterile impare ale lui
(in dezvoltare apar numai puterile impare ale lui
![]() )
)
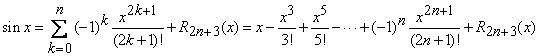 , (15)
, (15)
unde, restul sub forma lui Lagrange are expresia
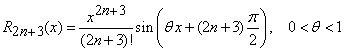 . (16)
. (16)
Din formula (16) deducem evaluarea .
.
Fie ![]() .
Atunci
.
Atunci ![]() si pentru orice
si pentru orice ![]() ,
avem
,
avem
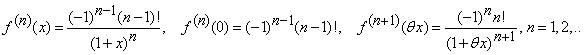
Atunci formula lui Taylor dupa puterile lui ![]() ,
devine
,
devine
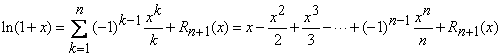 , (17)
, (17)
unde, restul sub forma lui Lagrange are expresia
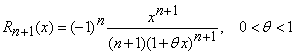 . (18)
. (18)
Daca ![]() din formula (18) obtinem
din formula (18) obtinem 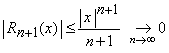 .
Daca
.
Daca ![]() atunci nu putem trage concluzii despre modul
cum restul tinde catre zero deoarece alegerea lui
atunci nu putem trage concluzii despre modul
cum restul tinde catre zero deoarece alegerea lui ![]() depinde atat de
depinde atat de ![]() cat si de
cat si de ![]() .
Folosind restul sub forma lui Cauchy,
.
Folosind restul sub forma lui Cauchy,
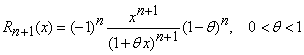 , (19)
, (19)
pe baza inegalitatilor ![]() ,
respectiv
,
respectiv ![]() ,
putem scrie evaluarea
,
putem scrie evaluarea
 .
.
Daca
![]() ,
atunci formula lui Taylor poate fi scrisa dar restul nu tinde catre zero cand
,
atunci formula lui Taylor poate fi scrisa dar restul nu tinde catre zero cand ![]() .
.
5.7. Observatie.
Daca in formula (17) schimbam ![]() cu
cu ![]() si cerem ca
si cerem ca ![]() ,
atunci obtinem dezvoltarea functiei
,
atunci obtinem dezvoltarea functiei ![]() dupa puterile lui
dupa puterile lui ![]() :
:
![]() , (17')
, (17')
Fie functia ![]() .
.
a)
Analizam
cazul cand ![]() .
Atunci functia
.
Atunci functia 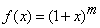 este bine definita pentru orice
este bine definita pentru orice
![]() si admite
derivate de orice ordin pe
si admite
derivate de orice ordin pe ![]() .
Cum derivata de ordinul
.
Cum derivata de ordinul ![]() a lui
a lui ![]() este identic nula, deducem ca
este identic nula, deducem ca ![]() si avem
si avem

Atunci pentru dezvoltarea functiei ![]() folosim binomul lui Newton
folosim binomul lui Newton
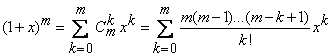 ,
pentru orice
,
pentru orice ![]() , (20)
, (20)
unde ![]() ,
reprezinta combinari de
,
reprezinta combinari de ![]() elemente luate cate
elemente luate cate ![]() ,
,
![]() .
.
b)
Pentru cazul
cand ![]() nu este numar natural, atunci functia
nu este numar natural, atunci functia ![]() este bine definita,
este bine definita,
impreuna cu toate derivatele sale de orice ordin,
pentru orice ![]() .
Asadar, pentru
.
Asadar, pentru ![]() putem scrie formulele
putem scrie formulele

si formula lui Taylor, scrisa in jurul punctului ![]() ,
devine
,
devine
![]() , (7.21)
, (7.21)
unde, restul sub forma lui Lagrange are expresia
![]() . (22)
. (22)
Daca ![]() si
si ![]() atunci restul tinde la zero cand
atunci restul tinde la zero cand ![]() .
In cazul cand
.
In cazul cand ![]() ,
folosind restul sub forma lui Cauchy
,
folosind restul sub forma lui Cauchy
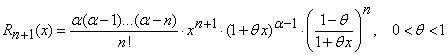 , (23)
, (23)
deducem ca restul
tinde la zero cand ![]() .
Pentru
.
Pentru ![]() restul nu tinde catre zero cand
restul nu tinde catre zero cand ![]() .
.
Serii Taylor
5.8. Fie functia ![]() si
si ![]() ,
oarecare, dar fixat. Presupunem ca functia
,
oarecare, dar fixat. Presupunem ca functia ![]() este indefinit derivabila intr-o vecinatate
este indefinit derivabila intr-o vecinatate ![]() (adica, functia
(adica, functia ![]() admite derivate de orice ordin intr-o
vecinatatea a punctului
admite derivate de orice ordin intr-o
vecinatatea a punctului ![]() ).
Atunci putem scrie formal seria Taylor
asociata functiei
).
Atunci putem scrie formal seria Taylor
asociata functiei ![]() in
punctul
in
punctul ![]()
![]() ,
, ![]() . (1)
. (1)
sau
seria de puteri a lui ![]() dupa puterile lui
dupa puterile lui ![]() .
Pentru valori fixate ale lui
.
Pentru valori fixate ale lui ![]() si
si ![]() seria poate fi convergenta sau divergenta. In
cazul cand seria Taylor asociata functiei
seria poate fi convergenta sau divergenta. In
cazul cand seria Taylor asociata functiei ![]() este convergenta atunci suma seriei este egala cu
este convergenta atunci suma seriei este egala cu ![]() .
.
Seria Taylor este convergenta catre functia ![]() daca si numai daca restul
daca si numai daca restul ![]() ,
al formulei lui Taylor
,
al formulei lui Taylor
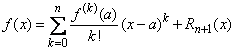 ,
, ![]() , (2)
, (2)
tinde la zero cand ![]() .
Altfel spus, daca
.
Altfel spus, daca ![]() ,
atunci din (2) rezulta ca sirul sumelor partiale
,
atunci din (2) rezulta ca sirul sumelor partiale
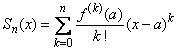 (3)
(3)
converge uniform catre ![]() pentru orice
pentru orice![]() si reciproc (vezi, siruri de functii).
si reciproc (vezi, siruri de functii).
In acest caz vom spune ca seria Taylor este convergenta avand suma egala cu ![]() si scriem
si scriem
![]() . (4)
. (4)
5.9. Observatie. Toate functiile analizate in
exemplele ![]() sunt dezvoltabile in serie Taylor dupa
puterile lui
sunt dezvoltabile in serie Taylor dupa
puterile lui ![]() (dezvoltabile in serie de puteri in jurul
punctului
(dezvoltabile in serie de puteri in jurul
punctului ![]() )
si avem:
)
si avem:
![]() . (5)
. (5)
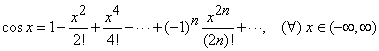 . (6)
. (6)
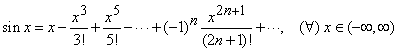 . (7)
. (7)
![]() . (8)
. (8)
![]() ,
,![]() . (9)
. (9)
Exercitiul 1. Sa se dezvolte in serie Taylor in jurul punctului ![]() functia
functia ![]() .
.
Indicatie. Fie ![]() .
Pentru calculul derivatelor de ordin superior ale lui
.
Pentru calculul derivatelor de ordin superior ale lui ![]() se poate folosi
se poate folosi
identitatea: ![]() .
Deducem ca
.
Deducem ca ![]() si
si ![]() ,
,
![]()
In consecinta, obtinem seria Taylor
![]()
5.10. Formula lui Taylor poate fi utilizata la
calculul "elegant" al unor limite de
functii, in cazurile de nedeterminare de tipul ![]() etc..
etc..
Exemple: 1). 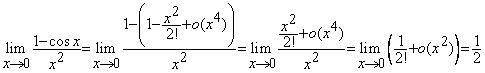 .
.
. 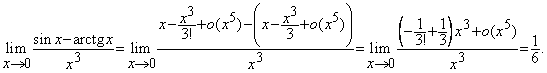
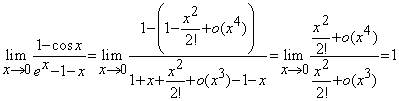 .
.
Calculati integrala ![]() cu o precizie mai mica decat
cu o precizie mai mica decat ![]() .
Avem
.
Avem
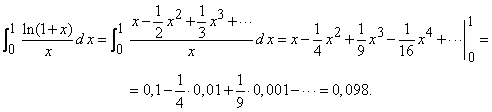
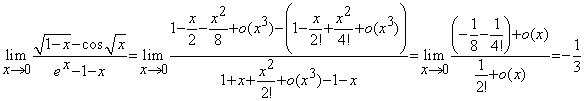 .
.
Calculati limitele: (i).![]() (ii).
(ii).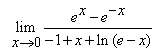 .
.
(iii). 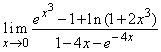 ; (iv).
; (iv). ![]() .
.
5.11. Observatie.
Exista functii de clasa ![]() pe
pe ![]() care nu sunt dezvoltabile in serie Taylor.
care nu sunt dezvoltabile in serie Taylor.
De exemplu, functia ![]() ,
definita prin
,
definita prin 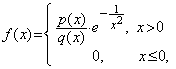 unde
unde
![]() sunt polinoame,
sunt polinoame, ![]() ,
este de clasa
,
este de clasa ![]() pe
pe
![]() ,
insa nu este dezvoltabila in serie Taylor in jurul punctului
,
insa nu este dezvoltabila in serie Taylor in jurul punctului ![]() .
.
Demonstratie. Aratam ca ![]() este
functie continua pe
este
functie continua pe ![]() .
Intr-adevar, prin definitie, functia
.
Intr-adevar, prin definitie, functia ![]() este continua pentru
este continua pentru ![]() .
In punctul
.
In punctul ![]() putem scrie
putem scrie
![]()
![]() si
si ![]() .
.
Deci ![]() este continua pe
este continua pe ![]() si
si ![]() .
.
Aratam ca ![]() si
si ![]() Intr-adevar, pentru
Intr-adevar, pentru ![]() avem
avem

unde ![]() sunt polinoame,
sunt polinoame, ![]() si
si ![]() .
.
Daca ![]() atunci
atunci ![]() .
Asadar, derivata in
.
Asadar, derivata in ![]() exista si este egala cu zero. Rezulta ca
exista si este egala cu zero. Rezulta ca ![]() este diferentiabila pe
este diferentiabila pe ![]() si derivata
si derivata ![]() are aceeasi forma cu
are aceeasi forma cu ![]() .
Prin recurenta deducem ca
.
Prin recurenta deducem ca ![]() este diferentiabila si are aceeasi forma cu
este diferentiabila si are aceeasi forma cu ![]() ,
deci
,
deci ![]() si avem
si avem ![]() .
.
Analog
se arata ca functia 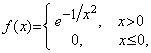 este de clasa
este de clasa ![]() pe
pe ![]() si nu este dezvoltabila in serie Taylor in
jurul punctului
si nu este dezvoltabila in serie Taylor in
jurul punctului ![]() .
.
Extreme libere. Maxime si minime relative
5.12. Definitie. Fie ![]() un spatiu metric si
un spatiu metric si ![]() .
Punctul
.
Punctul ![]() se numeste punct de maxim relativ pentru
se numeste punct de maxim relativ pentru ![]() (sau, functia
(sau, functia ![]() are in punctul
are in punctul ![]() un maxim
relativ) daca si numai daca exista o vecinatate
un maxim
relativ) daca si numai daca exista o vecinatate ![]() ,
,
![]() a.i.
a.i. ![]() .
.
In aceleasi conditii ca mai sus, punctul ![]() se numeste punct de minim relativ pentru
se numeste punct de minim relativ pentru ![]() (sau, functia
(sau, functia ![]() are in punctul
are in punctul ![]() un minim
relativ) daca si numai daca exista o vecinatate
un minim
relativ) daca si numai daca exista o vecinatate ![]() ,
,
![]() a.i.
a.i. ![]() .
.
Daca
proprietatile din definitie au loc pentru orice ![]() ,
atunci punctul
,
atunci punctul ![]() se numeste extrem
absolut (global) care poate fi un
maxim absolut, respectiv un minim absolut.
se numeste extrem
absolut (global) care poate fi un
maxim absolut, respectiv un minim absolut.
5.13. Teorema
lui Fermat . Fie ![]() un interval deschis si
un interval deschis si ![]() ,
,
![]() .
Daca
.
Daca ![]() este punct de extrem local pentru
este punct de extrem local pentru ![]() (maxim sau minim local) si
(maxim sau minim local) si ![]() este diferentiabila in
este diferentiabila in ![]() ,
atunci
,
atunci ![]() .
.
Demonstratie. Vom presupune ca ![]() este punct de maxim local. Atunci exista o
vecinatate
este punct de maxim local. Atunci exista o
vecinatate ![]() in
in ![]() ,
a.i.
,
a.i.![]() pentru orice
pentru orice ![]() .
Deoarece
.
Deoarece ![]() este diferentiabila in
este diferentiabila in ![]() ,
rezulta ca exista
,
rezulta ca exista ![]() si deci,
si deci,
![]() si
si ![]() .
.
Cum ![]() si
si ![]() atunci, datorita
atunci, datorita
egalitatii anterioare, deducem ![]() .
.
5.14.
Observatie. Conditia ![]() este o conditie necesara ca
este o conditie necesara ca ![]() sa fie un punct
de extrem local, dar in general nu este si suficienta. De exemplu, fie
functia
sa fie un punct
de extrem local, dar in general nu este si suficienta. De exemplu, fie
functia ![]() .
Atunci
.
Atunci ![]() derivabila pe
derivabila pe ![]() si
si ![]() desi
desi ![]() nu este punct de extrem local.
nu este punct de extrem local.
5.15. Teorema. Fie ![]() si
si ![]() .
Presupunem ca exista intervalul
.
Presupunem ca exista intervalul ![]() a.i.
a.i. ![]() ,
,
![]() diferentiabila pe
diferentiabila pe ![]() si
si ![]() iar
iar ![]() .
Atunci
.
Atunci ![]() este punct de maxim local pentru
este punct de maxim local pentru ![]() .
.
(Enuntati
teorema in cazul cand punctul ![]() este minim
local).
este minim
local).
Demonstratie. Deoarece ![]() pe
pe ![]() ,
atunci
,
atunci ![]() .
Din relatia
.
Din relatia ![]() pe
pe ![]() ,
rezulta ca
,
rezulta ca ![]() .
.
In concluzie, avem ![]() care arata ca
care arata ca ![]() este un maxim local pentru
este un maxim local pentru ![]() .
.
5.16. Teorema
lui Cauchy. Fie ![]() un interval oarecare (nu se precizeaza natura intervalului),
un interval oarecare (nu se precizeaza natura intervalului), ![]() si
si ![]() ,
avand proprietatile:
,
avand proprietatile:
i)
functiile ![]() sunt diferentiabile in
sunt diferentiabile in ![]() ;
;
ii)
![]()
iii)
![]()
atunci exista
o vecinatate ![]() ,
, ![]() continuta
in
continuta
in ![]() ,
a.i.
,
a.i. ![]() si avem
si avem
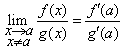
Demonstratie. Fie ![]() si
si ![]() (in cazul cand
(in cazul cand ![]() ,
atunci luam
,
atunci luam![]() ).
Daca
).
Daca ![]() si
si ![]() ,
atunci putem scrie
,
atunci putem scrie 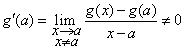 ,
deci exista o vecinatate
,
deci exista o vecinatate ![]() a lui
a lui ![]() continuta in
continuta in ![]() a.i. pentru orice
a.i. pentru orice ![]() sa avem
sa avem ![]() .
Cum
.
Cum ![]() ,
rezulta ca
,
rezulta ca ![]() .
Avem
.
Avem
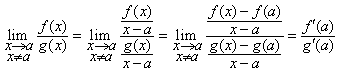
Exemplu. Consideram functile 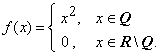 si
si ![]() .
.
Atunci ![]() ,
,
![]() este functie diferentiabila pe
este functie diferentiabila pe ![]() si
si ![]() ,
iar
,
iar ![]() este diferentiabila in
este diferentiabila in ![]() si
si ![]() .
Asadar, conditiile teoremei lui Cauchy sunt verificate si avem
.
Asadar, conditiile teoremei lui Cauchy sunt verificate si avem

5.17. Lema. Fie ![]() un interval oarecare (nu se precizeaza natura
intervalului),
un interval oarecare (nu se precizeaza natura
intervalului), ![]() ,
,
![]() o functie de
o functie de ![]() diferentiabila in
diferentiabila in ![]() ,
,
![]() .
Atunci exista
.
Atunci exista ![]() a.i. functia
a.i. functia ![]() este continua in
este continua in ![]() ,
,
![]() si sa avem egalitatea:
si sa avem egalitatea:
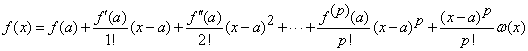 , (9.1)
, (9.1)
pentru orice ![]() .
.
Demonstratie. Definim functia
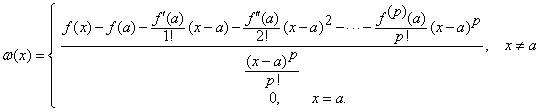
Aratam ca ![]() este functie continua in
este functie continua in ![]() ,
adica
,
adica ![]() .
.
Pentru ![]() avem
avem ![]() .
Aplicand teorema lui Cauchy, deducem, pentru
.
Aplicand teorema lui Cauchy, deducem, pentru ![]() ,
ca
,
ca ![]() .
.
Pentru ![]() avem
avem 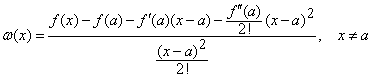 .
.
Se verifica, relativ usor, ca functiile care apar in
acest raport satisfac conditiile teoremei lui l'Hospital si deci, exista limita
![]() si avem
si avem ![]() .
.
Pentru calculul acestei limite vom observa ca sunt indeplinite conditiile teoremei lui Cauchy. Atunci, deducem
![]()
In cazul general, aplicand de ![]() teorema lui l´Hospital, deducem
teorema lui l´Hospital, deducem
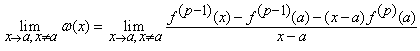
Apoi, aplicand teorema lui Cauchy, obtinem ![]() ,
deci functia
,
deci functia ![]() este continua in
este continua in ![]() .
.
5.18. Teorema. Fie ![]() un interval deschis,
un interval deschis, ![]() ,
,
![]() o functie
de
o functie
de ![]() diferentiabila
in
diferentiabila
in ![]() ,
,
![]() si
si ![]() ,
iar
,
iar ![]() .
Atunci
.
Atunci
1). Daca ![]() este numar par, atunci
este numar par, atunci ![]() este punct de extrem local pentru
este punct de extrem local pentru ![]() si avem:
si avem:
i). daca ![]() ,
atunci
,
atunci ![]() este punct
de maxim local;
este punct
de maxim local;
ii). daca ![]() ,
atunci
,
atunci ![]() este punct
de minim local.
este punct
de minim local.
2). Daca ![]() este numar impar si
este numar impar si ![]() ,
atunci
,
atunci ![]() nu este punct de extrem local pentru
nu este punct de extrem local pentru ![]() .
.
Demonstratie. Conform lemei, exista ![]() ,
,
![]() functie continua in
functie continua in ![]() ,
,
![]() ,
a.i.
,
a.i.
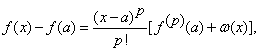 oricare ar fi
oricare ar fi ![]() .
.
Consideram functia ![]() ,
,
![]() .
Din felul cum a fost definita functia
.
Din felul cum a fost definita functia ![]() este continua in
este continua in ![]() si
si ![]() .
Presupunem
.
Presupunem ![]() ,
atunci exista o vecinatate
,
atunci exista o vecinatate ![]() care este continuta in
care este continuta in ![]() ,
a.i.
,
a.i. ![]() .
.
Fie ![]() numar par. Atunci
numar par. Atunci 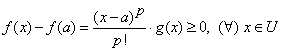 ,
deci
,
deci ![]() pentru orice
pentru orice ![]() si
si ![]() este punct de minim local pentru
este punct de minim local pentru ![]() .
.
Fie ![]() numar impar. Deoarece s-a admis ca
numar impar. Deoarece s-a admis ca ![]() ,
atunci avem
,
atunci avem ![]()
![]() si din relatia
si din relatia 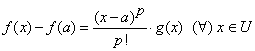 ,
rezulta ca diferenta
,
rezulta ca diferenta ![]() nu pastreaza semn constant. In adevar,
deoarece
nu pastreaza semn constant. In adevar,
deoarece ![]() pentru
pentru ![]() putem considera situatia
putem considera situatia ![]() si atunci avem
si atunci avem ![]() ,
iar pentru
,
iar pentru ![]() si
si ![]() ,
avem
,
avem ![]() .
.
Exerctiul 1. Aratati ca functia ![]() are un minim local in punctul
are un minim local in punctul ![]() .
.
Solutie. Determinam punctele
critice ale lui ![]() (acestea
sunt radacinile ecuatiei
(acestea
sunt radacinile ecuatiei ![]() ).
Avem
).
Avem ![]() si deci,
si deci, ![]() este singurul punct critic. Incercam sa vedem,
cu ajutorul derivatei de ordinul al doilea, daca acest punct critic este un
extrem local. Avem
este singurul punct critic. Incercam sa vedem,
cu ajutorul derivatei de ordinul al doilea, daca acest punct critic este un
extrem local. Avem ![]() si deci
si deci ![]() .
.
In acest caz nu putem preciza natura punctului critic ![]() si de aceea, studiem semnul derivatei de ordin
minim, care nu se anuleaza in acest punct. Asadar, calculam derivatele de ordin
superior. Obtinem
si de aceea, studiem semnul derivatei de ordin
minim, care nu se anuleaza in acest punct. Asadar, calculam derivatele de ordin
superior. Obtinem ![]()
![]() .
Prin urmare, in punctul critic
.
Prin urmare, in punctul critic ![]() avem:
avem:
![]() si
si ![]() ,
,
deci, punctul
critic ![]() este un punct de minim local.
este un punct de minim local.
Exerctiul 2. Determinati punctele de extrem local si valorile extreme ale functiei
![]()
Solutie. Punctele critice ale lui ![]() sunt radacinile ecuatiei
sunt radacinile ecuatiei ![]() .
Avem
.
Avem ![]() .
Deci,
.
Deci, ![]() si
si
![]() sunt singurele puncte critice. Fie
sunt singurele puncte critice. Fie ![]() .
Deoarece
.
Deoarece ![]() rezulta ca
rezulta ca ![]() este punct de minim local si valoarea minima a
lui
este punct de minim local si valoarea minima a
lui ![]() este
este ![]() .
In punctul critic
.
In punctul critic![]() avem
avem ![]() si nu putem decide natura acestui punct
critic. Observam ca
si nu putem decide natura acestui punct
critic. Observam ca ![]() ,
deci punctul
,
deci punctul ![]() nu este extrem local. Acesta este punct de
inflexiune (vezi fig. 1)
nu este extrem local. Acesta este punct de
inflexiune (vezi fig. 1)
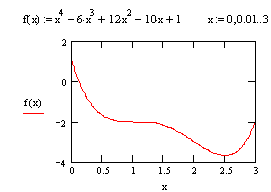
Figura 1.
Brook Taylor (1685-1731), matematician englez, membru al Royal Society din Londra. In lucrarea "Methodus incrementorum directa et inversa" (1715), expune metoda dezvoltarii in serie a unei functii. A pus, pentru prima data, problema coardei vibrante, de la care ulterior Fourier a ajuns la seriile trigonometrice.
Colin MacLaurin (1698-1746), matematician scotian. Numele sau este legat de calculul infinitesimal si in special de dezvoltarea functilor in serii de puteri.
Aceasta expresie se numeste restul sub forma lui Schlömilch . Schlömilch O.X. (1823-1901), matematician german.
Giuseppe Peano (1858-1932), logician si matematician italian. Profesor la Academia regala de artilerie si geniu si la Universitatea din Torino. In lucrarile sale a dat o prezentare axiomatica si deductiva a aritmeticii, geometriei proiective, teoriei multimilor etc.. Considera primul exemplu de curba continua, in sensul lui Jordan, care trece prin toate punctele interioare unui patrat.
Pierre Fermat (1601-1665), matematician
francez (autodidact). A facut studii de drept, a fost Consilier al
Parlamentului din Toulouse. Creator al geometriei analitice (ca si Descartes)
si al calculului probabilitatilor (alaturi de Pascal). A enuntat in 1637
formula celebra: ecuatia ![]() nu are solutii intregi
pentru
nu are solutii intregi
pentru ![]() (cunoscuta sub numele
de " Marea Teorema a lui Fermat"). Demonstratia acestei celebre teoreme a fost
data in 1995 de matematicianul englez Andrew Wiles, profesor la Universitatea
din Princeton.
(cunoscuta sub numele
de " Marea Teorema a lui Fermat"). Demonstratia acestei celebre teoreme a fost
data in 1995 de matematicianul englez Andrew Wiles, profesor la Universitatea
din Princeton.
|