Repartitii discrete
6.5.1.1 Repartitia discreta uniforma
Este una dintre cele mai simple repartitii. Probabilitatea totala, egala cu 1 sau 100%, se împarte în mod egal la mai multe posibilitati care pot apare în experimentul în care aceasta densitate intervine. De exemplu, prin aruncarea unui zar, se pot obtine cele sase valori corespunzatoare celor sase fete ale zarului, fiecare având probabilitatea 1/6.
În
acest caz, functia de repartitie este variabila aleatoare definita
de ![]() ,
, ![]() , adica
r r r r r r . Graficul acestei repartitii simple
este dat de figura 6.20:
, adica
r r r r r r . Graficul acestei repartitii simple
este dat de figura 6.20:
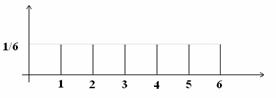
Figura 6.20 Repartitia discreta uniforma în cazul aruncarii unui zar
6.5.1.2. Repartitia binomiala
Este una dintre cele mai importante repartitii deoarece are aplicatii în statisticile epidemiologice si în toate statisticile unde intervin proportii. Daca într-o populatie, proportia indivizilor afectati de o maladie, (sau expusi la un factor de risc sau orice alta astfel de dichotomie), este p iar a celor neexpusi este q=1-p, atunci daca extragem aleator din populatie un numar de n indivizi, probabilitatea ca dintre ei, exact k sa fie afectati, este:
![]()
Densitatea de repartitie corespunzatoare este data de functia
![]() ,
, ![]()
Deci, o variabila aleatoare X, care se repartizeaza binomial, are urmatorul tabel al probabilitatilor:
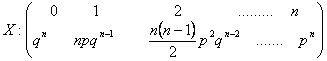
Caracteristicile de baza, anume valoarea asteptata si dispersia sunt:
![]() si
si ![]()
Aici este de fapt vorba de o infinitate de repartitii, deoarece poate fi schimbat si n si p. Daca n este în aplicatii numarul de indivizi extrasi de experimentator din populatie, adica este cunoscut, proportia p de indivizi afectati este de obicei necunoscuta si trebuie evaluata. În figurile sunt aratate graficele repartitiei binomiale pentru câteva valori ale lui n, de fiecare data pentru aceleasi valori ale lui p, din 0,1 în 0,1, de la 0,1 la 0,9.
Repartitia binomiala este asimetrica cu exceptia celei pentru p=0,5 pentru care este simetrica. Asimetria acestei repartitii este cu atât mai puternica cu cât n este mai mic. Pentru valori mari ale lui n, repartitia este aproximativ simetrica, atâta timp cât p nu este prea aproape de 0 sau de 1. Fiind o distributie discreta, repartitia nu este o curba ci poate fi reprezentata bine printr-o histograma
În figura 6.21 este reprezentata repartitia binomiala pentru n=5. Se obeserva ca este cu atât mai asimetrica, cu cât valoarea lui p este mai mica sau mai mare. Pentru p=0,5, repartitia este perfect simetrica
În figura 6.22 este reprezentata repartitia binomiala pentru n=15. Se obeserva ca este cu atât mai asimetrica, cu cât valoarea lui p este mai mica sau mai mare. Pentru p=0,5, repartitia este perfect simetrica. De asemenea, pentru p=0,4 si p=0,6, repartitia este foarte simetrica.
În figura 6.23 este reprezentata repartitia binomiala pentru n=50. Se obeserva ca este cu atât mai asimetrica, cu cât valoarea lui p este mai mica sau mai mare. Pentru p=0,5, repartitia este perfect simetrica. De asemenea, pentru p=0,4, p=0,6, p=0,3, p=0,7, repartitia este foarte simetrica. Practic, repartitia este simetrica pentru toate valorile lui p, exceptând p=0,1 si p=0,9.
În figura 6.24 este reprezentata repartitia binomiala pentru n=250. Se obeserva ca este simetrica pentru toate valorile lui p.
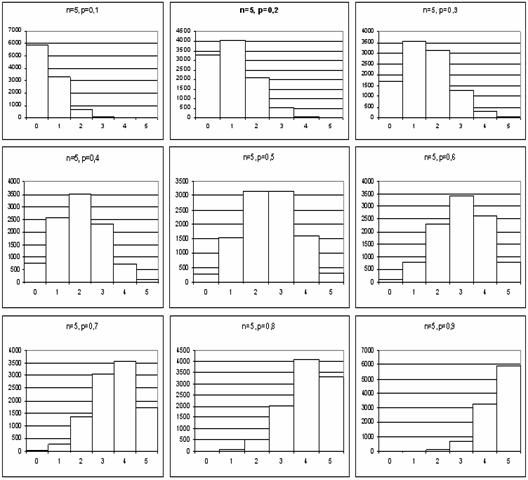
Figura 6.21 Repartitia binomiala pentru n=5 si pentru valori ale lui p de la 0,1 la 0,9, din 0,1 în 0,1. Se obeserva ca este cu atât mai asimetrica, cu cât valoarea lui p este mai mica sau mai mare. Pentru p=0,5, repartitia este perfect simetrica. Fiind o distributie discreta, repartitia nu este o curba ci poate fi reprezentata bine printr-o histograma
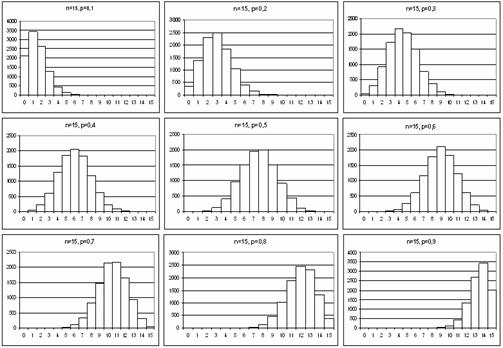
Figura 6.22 Repartitia binomiala pentru n=15 si pentru valori ale lui p de la 0,1 la 0,9, din 0,1 în 0,1. Se obeserva ca este cu atât mai asimetrica, cu cât valoarea lui p este mai mica sau mai mare. Pentru p=0,5, repartitia este perfect simetrica. De asemenea, pentru p=0,4 si p=0,6, repartitia este foarte simetrica. Fiind o distributie discreta, repartitia nu este o curba ci poate fi reprezentata bine printr-o histograma
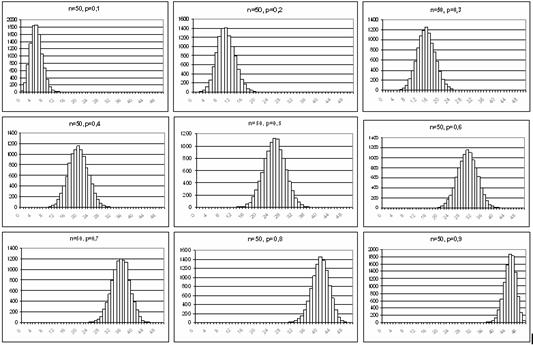
Figura 6.23 Repartitia binomiala pentru n=50 si pentru valori ale lui p de la 0,1 la 0,9, din 0,1 în 0,1. Se obeserva ca este cu atât mai asimetrica, cu cât valoarea lui p este mai mica sau mai mare. Pentru p=0,5, repartitia este perfect simetrica. De asemenea, pentru p=0,4, p=0,6, p=0,3, p=0,7, repartitia este foarte simetrica. Practic, reparrtitia este simetrica pentru toate valorile lui p, exceptând p=0,1 si p=0,9. Fiind o distributie discreta, repartitia nu este o curba ci poate fi reprezentata bine printr-o histograma
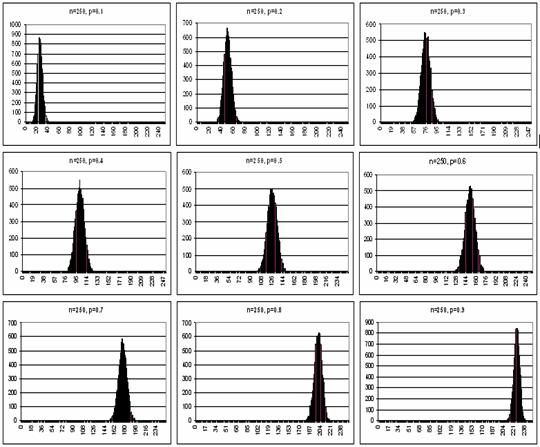
Figura 6.24 Repartitia binomiala pentru n=250 si pentru valori ale lui p de la 0,1 la 0,9, din 0,1 în 0,1. Se obeserva ca este simetrica pentru toate valorile lui p. Fiind o distributie discreta, repartitia nu este o curba ci poate fi reprezentata bine printr-o histograma
|