|
|
|
|
SPAŢII EUCLIDIENE
Parcurgând aceasta lectie ve ti dobândi cunostinte referitoare la:
Spatii vectoriale euclidiene;
Produs scalar, norma unghi, distanta;
Baze ortonormate, transformari ortogonale, procedee de ortogonalizare;
Operatori autoadjuncti pe spatii euclidiene;
Aducerea unei forme patratice la o suma de patrate prin metoda transformarilor ortogonale.
Timpul minim pe care trebuie sa-l acordati aces 13113f56n tei lectii este de 4 ore.
L.VI.2.1 Produs scalar, norma, unghi, distanta
Notiunea de produs scalar
În spatiul vectorial real tridimensional al vectorilor geometrici, reprezentati de sageti, am pus în evidenta si alte operatii în afara de cele care definesc structura de spatiu vectorial: produsul scalar, produsul vectorial, produsul mixt. Aceste operatii au fost definite, ca si cele de adunare si de înmultire a vectorilor cu numere, folosindu-se notiunile geometrice de unghi si distanta, de care nu dispunem în cazul spatiului real cu mai multe dimensiuni.
Notiunea de produs scalar, într-un spatiu oarecare, se defineste preluând proprietatile esentiale ale produsului scalar din spatiul fizic.
Definitie
Se numeste produs scalar pe spatiul vectorial real V o operatie în care la
fiecare
pereche de vectori x si y din V se asociaza un scalar
(numar real) notat ![]() astfel încât sunt îndeplinite urmatoarele conditii:
astfel încât sunt îndeplinite urmatoarele conditii:
![]() ;
;
![]() ;
;
![]() ;
;
![]() , daca si
numai daca
, daca si
numai daca ![]() .
.
Asa cum s-a stabilit în capitolul "Calculul vectorial", produsul scalar al vectorilor geometrici îndeplineste aceste conditii. Acest fapt are doua semnificatii. În primul rând el ofera un exemplu de produs scalar în sensul definit aici. Ca atare definitia este consistenta. În al doilea rând putem spune ca acest produs scalar este o generalizare a celui definit geometric în spatiul tridimensional.
Conditiile (2) si (3) exprima faptul ca produsul scalar, ca functie reala de doua variabile vectoriale x si y, este definit astfel încât, daca se fixeaza variabila x, se obtine o functie reala liniara în y. Conditia (1), de simetrie asigura ca produsul scalar este liniar si în x. Asadar, conditiile (1), (2) si (3) exprima faptul ca produsul scalar este o forma biliniara simetrica. Urmatoarea propozitie releva continutul conditiei (4).
Propozitie
O forma biliniara simetrica definita pe spatiul vectorial real V este produs scalar daca si numai daca forma patratica asociata ei este pozitiv definita.
Demonstratie
Fie o forma
biliniara simetrica![]() a spatiului V.
a spatiului V.
Notând ![]() , sunt îndeplinite conditiile (1), (2) si (3).
Daca forma patratica asociata
, sunt îndeplinite conditiile (1), (2) si (3).
Daca forma patratica asociata ![]() este pozitiv
definita, atunci exista o baza în care expresia formei
patratice este:
este pozitiv
definita, atunci exista o baza în care expresia formei
patratice este:
![]() ,
,
în care ![]() sunt coordonatele
vectorului x în acea baza.
Deoarece
sunt coordonatele
vectorului x în acea baza.
Deoarece ![]() este o suma de
patrate rezulta ca
este o suma de
patrate rezulta ca ![]() . În plus, suma de patrate
. În plus, suma de patrate ![]() daca si
numai daca toti termenii sumei sunt nuli, deci atunci si numai
atunci când
daca si
numai daca toti termenii sumei sunt nuli, deci atunci si numai
atunci când ![]() .
.
Reciproc,
sa presupunem ca forma biliniara simetrica din care provine
forma patratica ![]() este un produs scalar
adica îndeplineste conditia (4):
este un produs scalar
adica îndeplineste conditia (4): ![]() daca si
numai daca
daca si
numai daca ![]() . Fie
. Fie ![]() o baza în care
expresia formei patratice este o suma de patrate:
o baza în care
expresia formei patratice este o suma de patrate: ![]()
![]() . Rezulta ca pentru orice
. Rezulta ca pentru orice ![]() si deci
si deci ![]() , adica forma patratica
, adica forma patratica ![]() este pozitiv
definita. Q.E.D.
este pozitiv
definita. Q.E.D.
Din propozitia anterioara rezulta ca un produs scalar este o forma biliniara simetrica a carei forma patratica este pozitiv definita. Evident ca pe un spatiu vectorial real se pot defini mai multe produse scalare si anume atâtea câte forme patratice pozitiv definite sunt.
Daca
spatiul este finit generat, de dimensiune n, atunci multimea formelor patratice pozitiv definite
(deci a produselor scalare) este în corespondenta bijectiva cu
multimea matricelor patratice reale de ordinul n, simetrice, având toti minorii 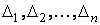 care au fost
definiti în metoda Iacobi strict pozitivi.
care au fost
definiti în metoda Iacobi strict pozitivi.
Notiunea de spatiu euclidian
Se
numeste spatiu euclidian un
spatiu vectorial real împreuna cu un produs scalar pe care-l vom nota
ca mai sus: ![]() înseamna produsul
scalar al vectorilor x si y. Pentru a desemna un spatiu
euclidian vom folosi de regula litera E
în loc de V.
înseamna produsul
scalar al vectorilor x si y. Pentru a desemna un spatiu
euclidian vom folosi de regula litera E
în loc de V.
Asa cum am mentionat, pe un spatiu vectorial real V exista o infinitate de produse scalare. Alegerea unuia dintre acestea confera spatiului V o structura algebrica prevazuta cu o operatie în plus fata de cele ale spatiului vectorial. Aceasta structura poarta numele de spatiu euclidian.
Inegalitatea lui Cauchy
Pentru
orice vector x al spatiului
euclidian E notam: ![]() .
.
Din definitia
produsului scalar, numarul de sub radical este pozitiv (chiar strict
pozitiv daca ![]() ), astfel încât radacina sa patratica
este corect definita ca numar real pozitiv si îl numim norma lui x. Pentru orice pereche de vectori x si y este
îndeplinita urmatoarea inegalitate numita inegalitatea lui Cauchy:
), astfel încât radacina sa patratica
este corect definita ca numar real pozitiv si îl numim norma lui x. Pentru orice pereche de vectori x si y este
îndeplinita urmatoarea inegalitate numita inegalitatea lui Cauchy:
![]() .
.
Într-adevar,
pentru orice numar real ![]() , din definitia produsului scalar, avem
, din definitia produsului scalar, avem ![]() , deci
, deci ![]() . Rezulta ca discriminantul acestui trinom de
gradul doi în
. Rezulta ca discriminantul acestui trinom de
gradul doi în ![]() este negativ:
este negativ: ![]() , de unde se obtine inegalitatea enuntata.
, de unde se obtine inegalitatea enuntata.
Inegalitatea triunghiului (Mincowski)
![]()
Pentru
demonstratie folosim proprietatile din definitia produsului
scalar: ![]() . Cu notatia introdusa aceasta înseamna:
. Cu notatia introdusa aceasta înseamna:
![]()
de unde, folosind inegalitatea lui Cauchy, ![]() , obtinem inegalitatea triunghiului.
, obtinem inegalitatea triunghiului.
Spatii normate, spatii Banach, spatii Hilbert.
Se
numeste norma pe
spatiul vectorial real V o
functie ![]() având urmatoarele
proprietati:
având urmatoarele
proprietati:
![]() daca si
numai daca
daca si
numai daca ![]() ;
;
![]() ;
;
![]() .
.
Un spatiu vectorial real se numeste spatiu vectorial normat daca pe acest spatiu s-a definit o norma.
Exemplu
În
orice spatiu euclidian E se
poate defini norma: ![]() . Din proprietatile produsului scalar si din
inegalitatile Cauchy si Mincowski, rezulta cele trei
conditii din definitia normei.
. Din proprietatile produsului scalar si din
inegalitatile Cauchy si Mincowski, rezulta cele trei
conditii din definitia normei.
Un vector al unui spatiu normat (în particular euclidian) se numeste versor daca are norma egala cu unu.
O
multime oarecare X se
numeste spatiu metric
daca exista o functie: ![]() numita distanta având
urmatoarele proprietati:
numita distanta având
urmatoarele proprietati:
![]() .
.
![]() .
.
![]() daca si
numai daca
daca si
numai daca ![]() .
.
Exemple
Pe
orice spatiu normat (si deci pe orice spatiu euclidian) se poate
defini distanta în felul urmator: ![]() . Folosind proprietatile din definitia normei
se pot demonstra cu usurinta proprietatile din
definitia distantei.
. Folosind proprietatile din definitia normei
se pot demonstra cu usurinta proprietatile din
definitia distantei.
Pe
un spatiu vectorial real se pot defini distante care sa nu
provina din nici-o norma, cum ar fi: ![]() pentru
pentru![]() si
si ![]() pentru
pentru ![]() .
.
Pe orice spatiu metric se poate defini o topologie cunoscuta sub numele de
"topologia spatiului metric". Mentionam ca un spatiu topologic se numeste spatiu topologic complet daca orice sir fundamental este convergent.
Se numeste spatiu Banach un spatiu normat care, cu topologia corespunzatoare, este complet. Daca, în plus, spatiul este euclidian, adica norma este definita de un produs scalar, atunci spatiul se numeste spatiu Hilbert.
Unghiul a doi vectori nenuli într-un spatiu euclidian
Fie
E un spatiu euclidian si x, y doi vectori nenuli din E. Numim unghiul vectorilor x si y, notat ![]() unghiul din intervalul
unghiul din intervalul
![]() definit de:
definit de:
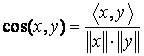 .
.
Inegalitatea
lui Cauchy asigura ca membrul drept al egalitatii este un
numar cuprins în intervalul ![]() deci poate fi
cosinusul unui unghi. Pe de alta parte, din monotonia functiei cos pe
intervalul
deci poate fi
cosinusul unui unghi. Pe de alta parte, din monotonia functiei cos pe
intervalul ![]() rezulta ca
acest unghi este determinat.
rezulta ca
acest unghi este determinat.
Spunem
ca vectorii x si y sunt ortogonali daca unghiul lor este drept. Acest lucru este
echivalent cu conditia: ![]() .
.
Alegând pe spatiul vectorial al vectorilor geometrici (definiti cu ajutorul sagetilor) produsul scalar obisnuit, unghiul definit mai sus este acelasi cu cel obtinut prin masurarea cu ajutorul raportorului. La fel, norma unui vector, coincide cu lungimea lui obtinuta prin masurarea cu ajutorul riglei gradata adecvat.
Daca însa alegem pe acest spatiu alt produs scalar, atunci nici lungimea vectorilor si nici unghiul lor nu vor mai fi aceleasi. De exemplu, pe de o parte se pierde atât calitatea de versor, cât si calitatea de vectori ortogonali, iar pe de alta parte unii vectori cu lungimea diferita de unu devin versori si alti vectori ce formeaza unghiuri ascutite sau obtuze devin ortogonali.
L.VI.2.2 Baze ortonormate, transformari ortogonale
Baze ortonormate
Fie
E un spatiu euclidian finit
generat. Se numeste baza
ortonormata o baza ![]() formata din
versori ortogonali doi câte doi.
formata din
versori ortogonali doi câte doi.
Din
definitia versorului si a unghiului a doi vectori rezulta
ca o baza ortonormata se caracterizeaza prin faptul ca
![]() simbolul lui Kronecker, care este
elementul generic al matricei unitate. Asadar o baza este ortonormata daca si numai daca
matricea produsului scalar, considerat ca forma biliniara
simetrica este tocmai matricea unitate
simbolul lui Kronecker, care este
elementul generic al matricei unitate. Asadar o baza este ortonormata daca si numai daca
matricea produsului scalar, considerat ca forma biliniara
simetrica este tocmai matricea unitate ![]() .
.
Reamintim ca daca A este matricea unei forme biliniare φ în baza :
![]() sunt coordonatele lui x,
iar
sunt coordonatele lui x,
iar ![]() sunt coordonatele lui y, atunci:
sunt coordonatele lui y, atunci:
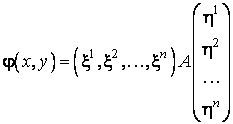 .
.
Luând în locul formei
φ produsul scalar, faptul ca, în acest caz, ![]() conduce la:
conduce la:
![]()
Asadar o baza ortonormata se poate caracteriza prin faptul ca produsul scalar a doi vectori este egal cu suma produselor coordonatelor corespunzatoare ale celor doi vectori în aceasta baza.
Metoda lui Gauss pentru construirea unei baze ortonormate
În capitolul anterior am aratat deja ca daca o forma patratica este pozitiv definita atunci exista o baza în care matricea sa este matricea unitate. Produsul scalar se defineste tocmai ca forma biliniara simetrica a carei forma patratica este pozitiv definita. Asadar exista o baza în care matricea produsului scalar este matricea unitate.
Reamintim procedeul
de obtinere a unei astfel de baze. Folosind metoda lui Gauss se aduce la o
suma de patrate forma patratica definita de produsul
scalar. Se obtine o baza ![]() în care matricea acestei
formei patratice este o matrice diagonala.
în care matricea acestei
formei patratice este o matrice diagonala.
Deoarece forma este
pozitiv definita elementele de pe diagonala sunt numere strict
pozitive. Faptul ca matricea produsului scalar este o matrice
diagonala înseamna ca ![]() pentru
pentru ![]() , adica vectorii
, adica vectorii ![]() sunt ortogonali doi
câte doi. Evident ca ei vor ramâne tot ortogonali daca vor fi
înmultiti cu scalari nenuli.
sunt ortogonali doi
câte doi. Evident ca ei vor ramâne tot ortogonali daca vor fi
înmultiti cu scalari nenuli.
Pe de alta parte
orice vector nenul x devine versor
daca se înmulteste cu scalarul ![]() . Într-adevar,
. Într-adevar,
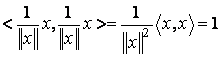 .
.
Operatia
prin care din vectorul nenul x
obtinem versorul  se numeste normare. Matricea coordonatelor
versorilor
se numeste normare. Matricea coordonatelor
versorilor ![]() în baza
în baza ![]() este matricea
diagonala având pe diagonala inversele normelor vectorilor
este matricea
diagonala având pe diagonala inversele normelor vectorilor ![]() , deci este o matrice nesingulara, de unde rezulta
ca acesti versori constituie o baza.
, deci este o matrice nesingulara, de unde rezulta
ca acesti versori constituie o baza.
Metoda lui Gramm de ortonormare
Urmatoarea
metoda descrie construirea pas cu pas a unei baze ortonormate. Fie ![]() o baza oarecare a
spatiului euclidian E si
notam
o baza oarecare a
spatiului euclidian E si
notam ![]() versorul obtinut prin normarea lui
versorul obtinut prin normarea lui ![]() .
.
Pentru
a obtine urmatorul versor al unei baze ortonormate calculam
vectorul auxiliar ![]() . În primul rând sa observam ca
. În primul rând sa observam ca ![]() deoarece
deoarece ![]() este o combinatie
liniara a vectorilor
este o combinatie
liniara a vectorilor ![]() în care coeficientul
lui
în care coeficientul
lui ![]() este egal cu unu
(vectorul
este egal cu unu
(vectorul ![]() se obtine prin
înmultirea vectorului
se obtine prin
înmultirea vectorului ![]() cu un numar). Pe
de alta parte,
cu un numar). Pe
de alta parte,
![]() ,
,
adica ![]() este ortogonal pe
este ortogonal pe ![]() . Notând cu
. Notând cu ![]() versorul obtinut
prin normarea lui
versorul obtinut
prin normarea lui ![]() , acesta va fi, de asemenea, ortogonal pe
, acesta va fi, de asemenea, ortogonal pe ![]() .
.
Analog, consideram vectorul auxiliar ![]() .
.
Deoarece ![]() si
si ![]() sunt combinatii
liniare numai de vectorii
sunt combinatii
liniare numai de vectorii ![]() rezulta ca
rezulta ca ![]() este o combinatie
liniara de vectorii liniar independenti
este o combinatie
liniara de vectorii liniar independenti ![]() în care
coeficientul lui
în care
coeficientul lui ![]() este nenul, deci
este nenul, deci ![]() .
.
Vom
arata ca ![]() este ortogonal si pe
este ortogonal si pe ![]() si pe
si pe ![]() .
.
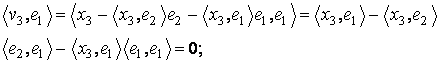
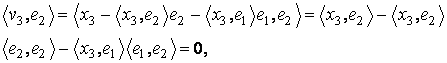
unde am folosit liniaritatea produsului scalar si ca
![]() .
.
Versorul
![]() al lui
al lui ![]() va fi iarasi
ortogonal si pe
va fi iarasi
ortogonal si pe ![]() si pe
si pe ![]() .
.
Se
continua acest procedeu pâna se obtin versorii ![]() ortogonali doi câte
doi. Acestia sunt liniar independenti deoarece daca
ortogonali doi câte
doi. Acestia sunt liniar independenti deoarece daca ![]() , înmultind scalar ambii membri ai acestei
egalitati cu versorul
, înmultind scalar ambii membri ai acestei
egalitati cu versorul ![]() se obtine
se obtine ![]() pentru orice indice i. Asadar ei formeaza o
baza.
pentru orice indice i. Asadar ei formeaza o
baza.
Este util de retinut ca orice sistem de n versori ortogonali doi câte doi constituie o baza.
În continuare vom studia multimea bazelor ortonormate ale unui spatiu euclidian finit generat.
Transformari ortogonale
Se
numeste transformare ortogonala
trecerea de la o baza ortonormata ![]() la o alta baza ortonormata
la o alta baza ortonormata ![]() .
.
Notând
![]() matricea de trecere,
observam ca:
matricea de trecere,
observam ca:
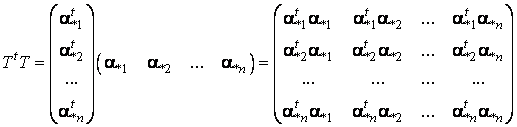 .
.
Ţinând
seama ca atât baza ![]() , cât si baza
, cât si baza ![]() sunt ortonormate
rezulta ca elementul generic al produsului TtT este:
sunt ortonormate
rezulta ca elementul generic al produsului TtT este:
![]()
adica ![]() . Asadar
. Asadar ![]() .
.
Mentionam
ca o matrice T care are
proprietatea: ![]() se numeste matrice ortogonala. Am ajuns la
concluzia ca matricea de trecere de
la o baza ortonormata la o alta baza ortonormata este
o matrice ortogonala.
se numeste matrice ortogonala. Am ajuns la
concluzia ca matricea de trecere de
la o baza ortonormata la o alta baza ortonormata este
o matrice ortogonala.
Reciproc,
daca baza ![]() este ortonormata,
atunci elementul generic al matricei
este ortonormata,
atunci elementul generic al matricei ![]() este
este ![]() . Daca, în plus, matricea T este ortogonala, atunci elementul generic al matricei
. Daca, în plus, matricea T este ortogonala, atunci elementul generic al matricei ![]() este
este ![]() , deci
, deci ![]() adica baza
adica baza ![]() este ortonormata.
este ortonormata.
În
concluzie, daca baza ![]() este ortonormata,
atunci
este ortonormata,
atunci ![]() este ortonormata
daca si numai daca matricea de trecere T este ortogonala.
este ortonormata
daca si numai daca matricea de trecere T este ortogonala.
În
acest fel, multimea bazelor ortonormate se identifica cu
multimea matricelor ortogonale de ordinul n. Aceasta multime se noteaza cu ![]() si se poate
usor verifica faptul ca este un grup fata de operatia de
înmultire a matricelor, numit grupul
ortogonal liniar.
si se poate
usor verifica faptul ca este un grup fata de operatia de
înmultire a matricelor, numit grupul
ortogonal liniar.
Proprietati ale matricelor ortogonale
I)
Daca matricea T a unui operator f al spatiului euclidian E
într-o baza ortonormata ![]() este ortogonala,
atunci matricea lui f în orice
alta baza ortonormata va fi tot ortogonala.
este ortogonala,
atunci matricea lui f în orice
alta baza ortonormata va fi tot ortogonala.
Într-adevar, fie
![]() o alta baza ortonormata, notam
o alta baza ortonormata, notam ![]() matricea de trecere de la baza
matricea de trecere de la baza ![]() la baza
la baza ![]() si S matricea lui f în baza
si S matricea lui f în baza ![]() . Ca si T,
matricele
. Ca si T,
matricele ![]() si S sunt ortogonale si
si S sunt ortogonale si ![]() . Rezulta:
. Rezulta:
![]() si
si ![]() adica
adica ![]() .
.
Definitie
I) Un operator f al spatiului euclidian E se numeste operator ortogonal daca matricea sa într-o baza ortonormata este ortogonala.
Consistenta acestei definitii se bazeaza pe proprietatea anterioara.
II)
Daca f este un operator
ortogonal al spatiului euclidian E,
atunci pentru orice vectori x si
y, ![]() . Altfel spus, un operator ortogonal pastreaza
produsul scalar.
. Altfel spus, un operator ortogonal pastreaza
produsul scalar.
Într-adevar,
fie T matricea lui f într-o baza ortonormata ![]() si
si
X, Y coloanele coordonatelor vectorilor x
si y în aceasta baza.
Rezulta ca T este
ortogonala si![]()
III)
Valorile proprii reale ale unei matrice ortogonale T sunt egale cu 1
sau -1.
Într-adevar,
fie f operatorul spatiului
euclidian E care în baza
ortonormata ![]() este reprezentat de
matricea T. Rezulta ca f este un operator ortogonal. Fie λ
o valoare proprie si v un vector
propriu corespunzator, adica
este reprezentat de
matricea T. Rezulta ca f este un operator ortogonal. Fie λ
o valoare proprie si v un vector
propriu corespunzator, adica ![]() . Rezulta pe de o parte ca
. Rezulta pe de o parte ca ![]() , iar pe de alta parte
, iar pe de alta parte ![]() . Asadar
. Asadar ![]() si cum
si cum ![]() deducem ca
deducem ca ![]() .
.
Transformarile ortogonale ale dreptei
Pentru
![]() matricea T se identifica cu un numar
real
matricea T se identifica cu un numar
real ![]() . Conditia
. Conditia ![]() revine la
revine la ![]() , de unde rezulta
, de unde rezulta ![]() . Grupul ortogonal de ordinul unu,
. Grupul ortogonal de ordinul unu, ![]() , se identifica cu grupul radacinilor de
ordinul doi ale unitatii. Daca fixam un punct pe o
dreapta, spatiul euclidian de dimensiune unu se identifica cu
multimea punctelor dreptei. Daca e
este unul din cei doi versori ai dreptei, atunci bazele e si -e constituie
cele doua baze ortonormate corespunzatoare celor doua elemente
ale grupului
, se identifica cu grupul radacinilor de
ordinul doi ale unitatii. Daca fixam un punct pe o
dreapta, spatiul euclidian de dimensiune unu se identifica cu
multimea punctelor dreptei. Daca e
este unul din cei doi versori ai dreptei, atunci bazele e si -e constituie
cele doua baze ortonormate corespunzatoare celor doua elemente
ale grupului ![]() .
.
Transformarile ortogonale ale planului
Determinam
mai întâi multimea matricelor ortogonale de ordinul doi. Daca 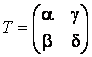 este o astfel de
matrice, atunci conditia
este o astfel de
matrice, atunci conditia ![]() este echivalenta
cu:
este echivalenta
cu:
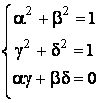 .
.
Prima
ecuatie a sistemului înseamna ca ![]() se pot scrie sub
forma:
se pot scrie sub
forma: ![]() . Analog, din a doua ecuatie rezulta:
. Analog, din a doua ecuatie rezulta: ![]() . În acest fel cele patru necunoscute s-au redus la
doua,
. În acest fel cele patru necunoscute s-au redus la
doua, ![]() situate în intervalul
situate în intervalul ![]() . Ele trebuie sa satisfaca ecuatia a treia,
adica:
. Ele trebuie sa satisfaca ecuatia a treia,
adica:
![]() .
.
Deoarece
![]() se afla în
intervalul
se afla în
intervalul ![]() rezulta ca:
rezulta ca: 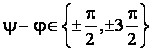 . În plus sa observam ca
. În plus sa observam ca ![]() determina
aceleasi valori pentru γ si
determina
aceleasi valori pentru γ si ![]() ca si
ca si ![]() . La fel,
. La fel, ![]() determina
aceleasi valori pentru γ si
determina
aceleasi valori pentru γ si ![]() ca si
ca si ![]() . Asadar sunt doua cazuri posibile.
. Asadar sunt doua cazuri posibile.
Cazul I. ![]() de unde
de unde 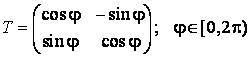 . Sa observam mai întâi ca toate matricele de
aceasta forma au determinantul egal cu unu.
. Sa observam mai întâi ca toate matricele de
aceasta forma au determinantul egal cu unu.
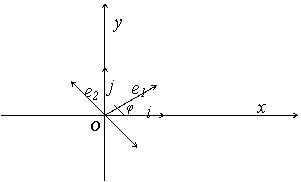
În
continuare ne propunem sa identificam bazele ortonormate reprezentate
de aceste matrice. Pornim de la baza ortonormata constituita de
versorii ![]() si
si ![]() ai axelor unui sistem
cartezian de axe ortogonale xOy.
Matricea T este matricea de trecere
de la aceasta baza la o alta baza ortonormata
formata din vectorii
ai axelor unui sistem
cartezian de axe ortogonale xOy.
Matricea T este matricea de trecere
de la aceasta baza la o alta baza ortonormata
formata din vectorii ![]() ale caror
coordonate în baza initiala sunt pe coloanele matricei T:
ale caror
coordonate în baza initiala sunt pe coloanele matricei T:
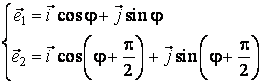
Vectorul
![]() se obtine prin
rotirea lui
se obtine prin
rotirea lui ![]() cu unghiul
cu unghiul ![]() în sens trigonometric
în jurul originii. La fel, vectorul
în sens trigonometric
în jurul originii. La fel, vectorul ![]() se obtine
prin rotirea lui
se obtine
prin rotirea lui ![]() cu unghiul
cu unghiul ![]() , ceea ce este acelasi lucru cu rotirea lui
, ceea ce este acelasi lucru cu rotirea lui ![]() cu unghiul
cu unghiul ![]() .
.
Prin
urmare, sistemul de vectori ![]() se obtine prin
rotirea sistemului rigid
se obtine prin
rotirea sistemului rigid ![]() cu unghiul
cu unghiul ![]() în sens trigonometric în jurul originii.
în sens trigonometric în jurul originii.
Cazul II. ![]() de unde
de unde 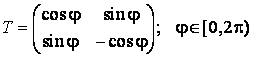 . Observam de aceasta data ca aceste
matrice au determinantul egal cu minus unu.
. Observam de aceasta data ca aceste
matrice au determinantul egal cu minus unu.
Vectorii
![]() ai noii baze,
reprezentate de matricea ortogonala T
sunt:
ai noii baze,
reprezentate de matricea ortogonala T
sunt:
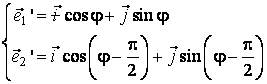 ,
,
adica ![]() , dar
, dar ![]()
Asadar,
noua baza ![]() se obtine prin
rotirea sistemului rigid de vectori
se obtine prin
rotirea sistemului rigid de vectori ![]() cu unghiul
cu unghiul ![]() urmata de
simetria acestui sistem fata de axa lui
urmata de
simetria acestui sistem fata de axa lui ![]() .
.
Transformari ortogonale în spatiu
Fie
T o matrice ortogonala de
ordinul trei pe care o interpretam ca matricea de trecere de la baza ![]() a versorilor axelor
unui triedru triortogonal Oxyz la o
alta baza ortonormata
a versorilor axelor
unui triedru triortogonal Oxyz la o
alta baza ortonormata ![]() .
.
Ne
propunem sa studiem operatorul liniar f
al spatiului euclidian tridimensional care în baza ![]() este reprezentat de
matricea T. În acest scop, îi punem
în evidenta valorile proprii si vectorii proprii.
este reprezentat de
matricea T. În acest scop, îi punem
în evidenta valorile proprii si vectorii proprii.
Polinomul
caracteristic al matricei T fiind de
gradul trei, el are cel putin o radacina reala ![]() . Una din proprietatile matricelor ortogonale
demonstrate mai sus atesta ca
. Una din proprietatile matricelor ortogonale
demonstrate mai sus atesta ca ![]() . Daca matricea T
nu are valoarea proprie
. Daca matricea T
nu are valoarea proprie ![]() , atunci sigur matricea -T
are aceasta valoare proprie. Deci putem presupune ca
, atunci sigur matricea -T
are aceasta valoare proprie. Deci putem presupune ca ![]() este valoare proprie a
matricei T.
este valoare proprie a
matricei T.
Fie
![]() un versor al
directiei vectorilor proprii corespunzatori valorii proprii
un versor al
directiei vectorilor proprii corespunzatori valorii proprii ![]() adica
adica ![]() . Completam sistemul liniar independent constituit de
vectorul
. Completam sistemul liniar independent constituit de
vectorul ![]() pâna la o
baza, pe care ortonormând-o prin procedeul lui Gramm obtinem baza
pâna la o
baza, pe care ortonormând-o prin procedeul lui Gramm obtinem baza ![]() .
.
Sa notam U matricea lui f în baza ![]() . Deoarece
. Deoarece ![]() rezulta ca
pe prima coloana se afla coordonatele lui
rezulta ca
pe prima coloana se afla coordonatele lui ![]() în baza
în baza ![]() adica 1, 0, 0. Fie
adica 1, 0, 0. Fie ![]() coordonatele lui
coordonatele lui ![]() în baza
în baza ![]() adica
adica ![]() .
.
Pe de o parte
![]() .
.
Pe de alta parte,
notând ![]() coloanele
coordonatelor vectorilor
coloanele
coordonatelor vectorilor ![]() , respectiv
, respectiv ![]() si tinând
seama ca
si tinând
seama ca ![]() , rezulta:
, rezulta:
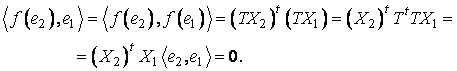
Asadar, ![]() . În mod analog, notând
. În mod analog, notând ![]() elementele celei de a
treia coloane a matrice U, care sunt
coordonatele lui
elementele celei de a
treia coloane a matrice U, care sunt
coordonatele lui ![]() în baza
în baza ![]() , ajungem la concluzia ca
, ajungem la concluzia ca ![]() . Deci matricea U
are forma:
. Deci matricea U
are forma:
 .
.
Sa aratam ca blocul
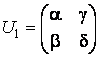 este o matrice
ortogonala de ordinul doi. Fie S
matricea de trecere de la baza
este o matrice
ortogonala de ordinul doi. Fie S
matricea de trecere de la baza ![]() la baza
la baza ![]() . Deoarece ambele baze sunt ortonormate, matricea S este ortogonala. Pe de alta
parte, din formula de transformare a matricei unui operator la schimbarea bazei
rezulta:
. Deoarece ambele baze sunt ortonormate, matricea S este ortogonala. Pe de alta
parte, din formula de transformare a matricei unui operator la schimbarea bazei
rezulta: ![]() . Deci matrice U ,
fiind un produs de matrice ortogonale, este ortogonala, adica
. Deci matrice U ,
fiind un produs de matrice ortogonale, este ortogonala, adica ![]() . De aici rezulta ca matricea
. De aici rezulta ca matricea ![]() este ortogonala.
este ortogonala.
Asadar,
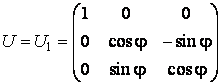 sau
sau 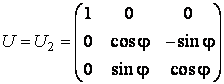
Interpretare geometrica
Sa
notam ![]() axele versorilor
axele versorilor ![]() respectiv. Reamintim
ca asociind punctelor vectorii lor de pozitie (cu sursa în O) coordonatele carteziene ale unui
punct în reperul cartezian OXYZ sunt
coordonatele vectorului de pozitie în baza
respectiv. Reamintim
ca asociind punctelor vectorii lor de pozitie (cu sursa în O) coordonatele carteziene ale unui
punct în reperul cartezian OXYZ sunt
coordonatele vectorului de pozitie în baza ![]() .
.
Fie
v vectorul de pozitie al
punctului oarecare P. Vrem sa
vedem ce devine ![]() . Vectorul v se
descompune
. Vectorul v se
descompune ![]() în care
în care ![]() este proiectia
lui v pe axa OX, deci are directia lui
este proiectia
lui v pe axa OX, deci are directia lui ![]() iar
iar ![]() este în planul OYZ, adica este o combinatie
liniara de
este în planul OYZ, adica este o combinatie
liniara de ![]() . Deoarece
. Deoarece ![]() rezulta ca
rezulta ca![]() .
.
Daca
![]() atunci
atunci ![]() se obtine prin
rotirea lui
se obtine prin
rotirea lui ![]() cu unghiul
cu unghiul ![]() în planul YOZ în sens trigonometric privit din
semispatiul în care se afla axa OX.
Rezulta ca vectorul v (deci
punctul P) se roteste în jurul axei lui
în planul YOZ în sens trigonometric privit din
semispatiul în care se afla axa OX.
Rezulta ca vectorul v (deci
punctul P) se roteste în jurul axei lui ![]() cu unghiul
cu unghiul ![]() în sensul dat de regula surubului drept.
în sensul dat de regula surubului drept.
Daca
![]() atunci
atunci ![]() se obtine din
rotirea ca mai sus a lui
se obtine din
rotirea ca mai sus a lui ![]() urmata de
simetria fata de axa lui
urmata de
simetria fata de axa lui ![]() . Transformarea
. Transformarea ![]() a vectorului v este aceeasi rotire a lui v descrisa mai înainte, urmata de simetria fata de
planul determinat de
a vectorului v este aceeasi rotire a lui v descrisa mai înainte, urmata de simetria fata de
planul determinat de ![]() si
si ![]() .
.
Sa mai observam ca trecerea de la f la -f înseamna simetria fata de origine care este compunerea a trei simetrii fata de plane.
În concluzie orice transformare ortogonala este o rotatie în jurul unei axe urmata, eventual, de o simetrie fata de un plan.
Deoarece produsul a doua matrice ortogonale este tot o matrice ortogonala rezulta ca rezultatul rotirii succesive în jurul unor axe este rotirea în jurul unei a treia axe.
L.VI.2.3 Operatori simetrici în spatii euclidiene
Adjunctul unui operator
Pe
spatiul euclidian E se
considera operatorii ![]() care în baza
ortonormata
care în baza
ortonormata ![]() sunt reprezentati
de matricele
sunt reprezentati
de matricele ![]() , respectiv
, respectiv ![]() . Sa observam ca daca
. Sa observam ca daca ![]() , atunci în orice alta baza ortonormata
matricea lui
, atunci în orice alta baza ortonormata
matricea lui ![]() este transpusa
matricei lui
este transpusa
matricei lui ![]() .
.
Într-adevar,
fie ![]() o alta baza
ortonormata si T matricea
de trecere de la baza
o alta baza
ortonormata si T matricea
de trecere de la baza ![]() la baza
la baza ![]() . Matricea T este
ortogonala. Matricele
. Matricea T este
ortogonala. Matricele ![]() ale operatorilor
ale operatorilor ![]() , respectiv
, respectiv ![]() în noua baza
sunt:
în noua baza
sunt:
![]()
si deci:
![]() .
.
Aceasta constatare da sens urmatoarei definitii.
Definitie
Fie
f un operator liniar al
spatiului euclidian finit generat E.
Se numeste adjunctul operatorului f,
operatorul ![]() a carui matrice
într-o baza ortonormata este transpusa matricei lui f în acea baza.
a carui matrice
într-o baza ortonormata este transpusa matricei lui f în acea baza.
Pentru adjunctul unui operator se poate da o caracterizare "intrinseca", adica fara sa facem apel la o baza a spatiului.
Propozitie
Fie
f un operator liniar al
spatiului euclidian finit generat E.
Operatorul g este adjunctul lui f daca si numai daca
pentru orice pereche de vectori x si
y din E se îndeplineste relatia: ![]() .
.
Demonstratie
Fie ![]() o baza
ortonormata, A si B matricele operatorilor f, respectiv g în aceasta
baza, X si Y coloanele coordonatelor vectorilor x, respectiv y.
o baza
ortonormata, A si B matricele operatorilor f, respectiv g în aceasta
baza, X si Y coloanele coordonatelor vectorilor x, respectiv y.
Daca
g este adjunctul lui f , atunci ![]() si deci:
si deci:
![]() .
.
Reciproc,
presupunem ca pentru orice pereche de vectori x si y este
îndeplinita relatia: ![]() . Aceasta relatie este echivalenta cu:
. Aceasta relatie este echivalenta cu: ![]() sau:
sau: ![]() pentru orice pereche
de matrici coloana X si Y. Rezulta atunci
pentru orice pereche
de matrici coloana X si Y. Rezulta atunci ![]() adica
adica ![]() . Q.E.D.
. Q.E.D.
Operatori simetrici. Proprietati
Operatorul
f al spatiului euclidian finit
generat E se numeste operator simetric sau autoadjunct daca ![]() .
.
Daca
A este matricea lui f într-o baza ortonormata,
atunci conditia ca f sa fie
simetric este echivalenta cu: ![]() . Deci un operator este
simetric daca si numai daca matricea sa într-o baza
ortonormata este simetrica.
. Deci un operator este
simetric daca si numai daca matricea sa într-o baza
ortonormata este simetrica.
În continuare, mentionam doua proprietati remarcabile ale operatorilor simetrici.
Propozitia 1
Valorile proprii ale unui operator simetric al unui spatiu euclidian finit generat sunt numere reale.
Demonstratie.
Fie f un operator simetric, A matricea sa în baza ortonormata ![]() si
si ![]() o valoare proprie.
Deoarece
o valoare proprie.
Deoarece ![]() , sistemul omogen
, sistemul omogen ![]() are cel putin o
solutie nebanala
are cel putin o
solutie nebanala ![]() , formata din numere, în principal, complexe daca
, formata din numere, în principal, complexe daca ![]() este un numar
complex. Din sistem rezulta
este un numar
complex. Din sistem rezulta ![]()
Conjugata unei matrice se obtine înlocuind elementele matricei cu conjugatele lor. Din regulile de calcul cu numere complexe rezulta ca produsul conjugatelor a doua matrice este conjugatul produsului matricelor. În plus, deoarece A este reala, rezulta:
![]() .
.
Mai departe,
tinând seama ca ![]() , obtinem:
, obtinem:
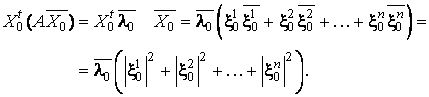
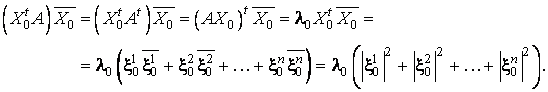
Din
asociativitatea înmultirii matricelor si din faptul ca ![]() este solutie
nebanala a sistemului, deducem ca
este solutie
nebanala a sistemului, deducem ca ![]() , adica
, adica ![]() este numar real.
Q.E.D.
este numar real.
Q.E.D.
Propozitia 2
Vectorii proprii ai unui operator simetric corespunzatori la valori proprii distincte sunt ortogonali.
Demonstratie
Fie f un operator simetric ![]() al spatiului
euclidian E si
al spatiului
euclidian E si ![]() vectori proprii
corespunzatori la doua valori proprii distincte
vectori proprii
corespunzatori la doua valori proprii distincte ![]() , adica
, adica![]() .
.
Pe
de o parte, ![]() . Pe de alta parte,
. Pe de alta parte, ![]()
Rezulta
![]() .
.
Cum ![]() , înseamna ca
, înseamna ca ![]() . Q.E.D.
. Q.E.D.
Teorema fundamentala a operatorilor simetrici
Teorema
Orice operator simetric al unui spatiu euclidian finit generat admite o baza ortonormata formata din vectori proprii.
Demonstratie
Efectuam demonstratia prin inductie dupa dimensiunea n a spatiului.
Etapa
de verificare. Daca ![]() , atunci orice vector nenul al spatiului este vector
propriu. Normând un vector oarecare nenul, versorul obtinut constituie o
baza ortonormata formata dintr-un singur vector care este vector
propriu.
, atunci orice vector nenul al spatiului este vector
propriu. Normând un vector oarecare nenul, versorul obtinut constituie o
baza ortonormata formata dintr-un singur vector care este vector
propriu.
Etapa de demonstratie
Ipoteza
Orice operator simetric al unui spatiu euclidian de dimensiune n admite o baza ortonormata formata din vectori proprii.
Concluzia
Orice operator simetric al unui spatiu euclidian de dimensiune n + 1 admite o baza ortonormata formata din vectori proprii.
Demonstratie
Fie f un operator simetric al spatiului
euclidian E de dimensiune ![]() . Propozitia 2. asigura ca operatorul f admite cel putin o valoare
proprie reala
. Propozitia 2. asigura ca operatorul f admite cel putin o valoare
proprie reala ![]() . Notam
. Notam ![]() un vector propriu
corespunzator acestei valori proprii.
un vector propriu
corespunzator acestei valori proprii.
Sistemul
format din singurul vector ![]() este liniar
independent (fiind vector nenul), deci se poate completa pâna la o baza:
exista vectorii
este liniar
independent (fiind vector nenul), deci se poate completa pâna la o baza:
exista vectorii ![]() , astfel încât
, astfel încât ![]() constituie o baza
a lui E. Fie
constituie o baza
a lui E. Fie ![]() baza ortonormata
obtinuta prin procedeul lui Gramm.
baza ortonormata
obtinuta prin procedeul lui Gramm.
Conform
acestei metode vectorul ![]() se obtine
prin normarea lui
se obtine
prin normarea lui ![]() adica prin
înmultirea lui
adica prin
înmultirea lui ![]() cu un anumit
numar nenul. Deoarece
cu un anumit
numar nenul. Deoarece ![]() este vector propriu
corespunzator valorii proprii
este vector propriu
corespunzator valorii proprii ![]() , rezulta ca la fel este si versorul
, rezulta ca la fel este si versorul ![]() , adica
, adica ![]() .
.
Notând cu ![]() matricea lui f în aceasta baza, prima
coloana a acestei matrici este constituita din numerele:
matricea lui f în aceasta baza, prima
coloana a acestei matrici este constituita din numerele: ![]() , care sunt
coordonatele lui
, care sunt
coordonatele lui ![]() în baza
în baza ![]() .
.
Pe de alta
parte, operatorul f fiind simetric
si baza ![]() fiind ortonormata
rezulta ca matricea
fiind ortonormata
rezulta ca matricea ![]() este simetrica.
Deci aceleasi numere
este simetrica.
Deci aceleasi numere ![]() constituie si
prima linie a matricei
constituie si
prima linie a matricei ![]() . Asadar matricea A
are forma:
. Asadar matricea A
are forma:

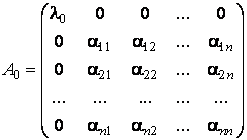
Notam
cu E
subspatiul generat de vectorii: ![]() . Ca orice subspatiu al unui spatiu euclidian,
subspatiul
. Ca orice subspatiu al unui spatiu euclidian,
subspatiul ![]() este si el un
spatiu euclidian (produsul scalar se ia acelasi cu cel din E). Subspatiul euclidian
este si el un
spatiu euclidian (produsul scalar se ia acelasi cu cel din E). Subspatiul euclidian ![]() are dimensiunea n, vectorii
are dimensiunea n, vectorii ![]() constituind o
baza ortonormata a acestui spatiu.
constituind o
baza ortonormata a acestui spatiu.
Fie
f ' restrictia lui f la subspatiul ![]() . Aceasta restrictie este, în principiu o aplicatie liniara de la E' la E. Dar cum a doua coloana a
matricei
. Aceasta restrictie este, în principiu o aplicatie liniara de la E' la E. Dar cum a doua coloana a
matricei ![]() este constituita
din coordonatele lui
este constituita
din coordonatele lui ![]() în baza
în baza ![]() , rezulta ca:
, rezulta ca:
![]() .
.
La fel se
arata ca si ceilalti vectori, ![]() sunt în
sunt în ![]() . Asadar în realitate
f ' este un operator liniar al lui
. Asadar în realitate
f ' este un operator liniar al lui ![]() . Matricea operatorului f
' al lui
. Matricea operatorului f
' al lui ![]() este tocmai blocul
este tocmai blocul ![]() al lui
al lui ![]() care este evident o matrice
simetrica din moment ce întreaga matrice
care este evident o matrice
simetrica din moment ce întreaga matrice ![]() este simetrica.
Deoarece matricea A a operatorului
este simetrica.
Deoarece matricea A a operatorului ![]() al spatiului
euclidian
al spatiului
euclidian ![]() în baza
ortonormata
în baza
ortonormata ![]() este simetrica,
rezulta ca operatorul
este simetrica,
rezulta ca operatorul ![]() este simetric.
este simetric.
Aplicând
ipoteza de inductie ![]() deducem ca
exista o baza
deducem ca
exista o baza ![]() a lui
a lui ![]() , tot ortonormata ca si
, tot ortonormata ca si ![]() , dar formata din vectori proprii.
, dar formata din vectori proprii.
Sa
aratam ca vectorii: ![]() constituie o baza ortonormata a lui
constituie o baza ortonormata a lui ![]() formata din
vectori proprii ai lui f.
formata din
vectori proprii ai lui f.
În
primul rând, versorii ![]() fiind vectori proprii
ai lui
fiind vectori proprii
ai lui ![]() , ei sunt, evident, vectori proprii si pentru f. Deci toti vectorii:
, ei sunt, evident, vectori proprii si pentru f. Deci toti vectorii: ![]() sunt vectori proprii
ai lui f. Pe de alta parte,
vectorul
sunt vectori proprii
ai lui f. Pe de alta parte,
vectorul ![]() fiind ortogonal pe
generatorii
fiind ortogonal pe
generatorii ![]() ai subspatiului
ai subspatiului ![]() va fi ortogonal pe
orice vector al acestui spatiu, deci implicit pe vectorii
va fi ortogonal pe
orice vector al acestui spatiu, deci implicit pe vectorii ![]() . Asadar, versorii
. Asadar, versorii ![]()
sunt ortogonali doi câte doi, deci ei constituie o baza ortonormata a
spatiului E. Q. E. D.
Metoda transformarii ortogonale de aducere a unei forme patratice la o suma de patrate.
În cazul spatiului euclidian, pe lânga metodele Gauss si Iacobi, vom elabora înca o metoda de aducere a unei forme patratice la o suma de patrate.
Consideram
![]() o forma
patratica a spatiului euclidian E care în baza ortonormata
o forma
patratica a spatiului euclidian E care în baza ortonormata ![]() este reprezentata
de matricea simetrica A.
este reprezentata
de matricea simetrica A.
Aceeasi matrice A poate reprezenta un operator f al spatiului E. Matricea A fiind simetrica si baza fiind ortonormata rezulta ca operatorul f este simetric.
Conform
teoremei fundamentale a operatorilor simetrici exista o baza
ortonormata ![]() a spatiului E constituita din vectori proprii
ai lui f. Notând cu T matricea de trecere de la baza
a spatiului E constituita din vectori proprii
ai lui f. Notând cu T matricea de trecere de la baza ![]() la baza
la baza ![]() , aceasta este o matrice ortogonala
, aceasta este o matrice ortogonala ![]() , iar matricea B a
lui f în noua baza va fi:
, iar matricea B a
lui f în noua baza va fi:
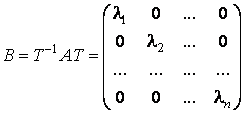 ,
,
în care ![]() sunt valorile proprii
ale matricei A.
sunt valorile proprii
ale matricei A.
Deoarece
![]() rezulta ca
matricea formei patratice
rezulta ca
matricea formei patratice ![]() în noua baza
va fi:
în noua baza
va fi: ![]() . Asadar matricea lui
. Asadar matricea lui ![]() în noua baza este
o matrice diagonala. Ca urmare, expresia formei patratice
în noua baza este
o matrice diagonala. Ca urmare, expresia formei patratice ![]() în aceasta
baza este o suma de patrate, coeficientii patratelor
fiind elementele de pe diagonala matricei B.
în aceasta
baza este o suma de patrate, coeficientii patratelor
fiind elementele de pe diagonala matricei B.
În
concluzie putem formula urmatoarea metoda de aducere a unei forme
patratice la o suma de patrate, numita "metoda
transformarii ortogonale": Se calculeaza valorile proprii ale
matricei A a formei patratice ![]() într-o baza
ortonormata. Aceste valori proprii stim ca sunt reale. Ele
constituie coeficientii patratelor în noua expresie a formei. Baza în
care forma
într-o baza
ortonormata. Aceste valori proprii stim ca sunt reale. Ele
constituie coeficientii patratelor în noua expresie a formei. Baza în
care forma ![]() are aceasta
noua expresie este o baza ortonormata formata din vectori
proprii ai matricei A. Teorema
fundamentala a operatorilor simetrici ne asigura ca exista
o astfel de baza.
are aceasta
noua expresie este o baza ortonormata formata din vectori
proprii ai matricei A. Teorema
fundamentala a operatorilor simetrici ne asigura ca exista
o astfel de baza.
Exemplu
Consideram
spatiul euclidian ![]() în care produsul scalar este definit,
astfel încât baza canonica este o baza ortonormata. Ne propunem
sa aducem la o suma de patrate forma patratica:
în care produsul scalar este definit,
astfel încât baza canonica este o baza ortonormata. Ne propunem
sa aducem la o suma de patrate forma patratica:
![]() ,
,
în care ![]() sunt coordonatele
vectorului variabil x în baza
canonica
sunt coordonatele
vectorului variabil x în baza
canonica ![]() . Matricea formei este:
. Matricea formei este:
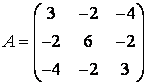 .
.
Coeficientii
polinomului caracteristic sunt: ![]() . Deci polinomul caracteristic este:
. Deci polinomul caracteristic este: ![]() care are
radacinile:
care are
radacinile: ![]()
Deci expresia formei patratice este:
![]() ,
,
în care ![]() sunt coordonatele
vectorului variabil x într-o
noua baza ortonormata
sunt coordonatele
vectorului variabil x într-o
noua baza ortonormata ![]() formata din
vectori proprii ai matricei A.
formata din
vectori proprii ai matricei A.
Determinam
aceasta baza. Pentru ![]() sistemul din care
se determina vectorii proprii este:
sistemul din care
se determina vectorii proprii este:
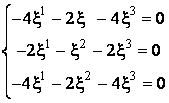
Ecuatiile fiind
proportionale sistemul este dublu nedeterminat, asa cum era de
asteptat deoarece valoarea proprie ![]() este dubla.
Luând ca necunoscute secundare
este dubla.
Luând ca necunoscute secundare ![]() , în spatiul bidimensional al solutiilor sistemului
se alege o baza formata din doi vectori, si anume:
, în spatiul bidimensional al solutiilor sistemului
se alege o baza formata din doi vectori, si anume:
-
din ![]() rezulta
rezulta ![]() si deci am
obtinut vectorul
si deci am
obtinut vectorul ![]() ;
;
-
din ![]() rezulta
rezulta ![]() si deci am
obtinut vectorul
si deci am
obtinut vectorul ![]() .
.
Folosind
procedeul lui Gramm, din baza ![]() a subspatiului
vectorilor proprii corespunzatori valorii proprii
a subspatiului
vectorilor proprii corespunzatori valorii proprii ![]() , se obtine o baza ortonormata
, se obtine o baza ortonormata ![]() :
:
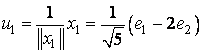 .
.
Pentru a afla pe ![]() se calculeaza mai întâi vectorul auxiliar
se calculeaza mai întâi vectorul auxiliar ![]() :
:
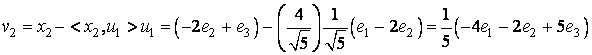
si apoi:
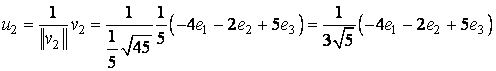 .
.
Pentru ![]() se obtine
sistemul:
se obtine
sistemul:
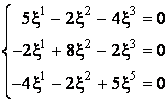 ,
,
care se rezolva prin metoda eliminarii succesive:
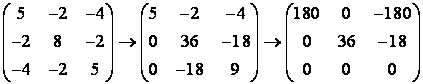 .
.
Sistemul
este simplu nedeterminat având ca necunoscuta secundara x careia-i atribuim valoarea arbitrara ![]() . Se obtine:
. Se obtine: ![]() ,
,![]() , deci vectorul
, deci vectorul ![]() . Se determina α, astfel încât v sa devina versor:
. Se determina α, astfel încât v sa devina versor:
![]() .
.
Luând, de exemplu ![]() se obtine:
se obtine: ![]() care împreuna cu
care împreuna cu ![]() constituie o baza
ortonormata formata din vectori proprii ai matricei A.
constituie o baza
ortonormata formata din vectori proprii ai matricei A.
L.VI.2.4 PROBLEME PROPUSE
PP.VI.2.4.1 Fie ![]() si
si ![]() doi vectori oarecare
din spatiul vectorial real
doi vectori oarecare
din spatiul vectorial real ![]() . Sa se cerceteze care dintre expresiile urmatoare
defineste un produs scalar pe
. Sa se cerceteze care dintre expresiile urmatoare
defineste un produs scalar pe ![]() :
:
a)
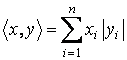 ;
;
b)
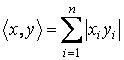 ;
;
c)
 ;
;
d)
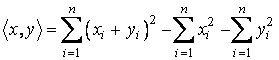 .
.
PP.VI.2.4.2 Fie ![]() spatiul
spatiul vectorial real al functiilor polinomiale reale definite pe
intervalul
spatiul
spatiul vectorial real al functiilor polinomiale reale definite pe
intervalul ![]() .
.
a)
Sa
se arate ca ![]() formeaza o
baza în
formeaza o
baza în ![]() ;
;
b) Sa se demonstreze ca ![]() este un spatiu
euclidian în raport cu aplicatia definita prin:
este un spatiu
euclidian în raport cu aplicatia definita prin: 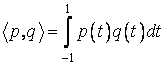 ;
;
c) Polinoamele obtinute din baza
canonica ![]() prin procedeul de
ortogonalizare se numesc polinoame Legendre. Sa se scrie primele cinci
polinoame Legendre.
prin procedeul de
ortogonalizare se numesc polinoame Legendre. Sa se scrie primele cinci
polinoame Legendre.
PP.VI.2.4.3 Fie ![]() un spatiu
euclidian,
un spatiu
euclidian, ![]() un subspatiu al
sau si
un subspatiu al
sau si ![]() produsul scalar în
spatiul
produsul scalar în
spatiul ![]() . Sa se arate ca:
. Sa se arate ca:
a) Multimea ![]() este un subspatiu
al lui
este un subspatiu
al lui ![]() (numit subspatiul
ortogonal al lui
(numit subspatiul
ortogonal al lui ![]() );
);
b) Subspatiile ![]() si
si ![]() admit suma
directa;
admit suma
directa;
c) ![]() .
.
PP.VI.2.4.4 Pe spatiul vectorial real al
functiilor continue ![]() , se defineste aplicatia:
, se defineste aplicatia: 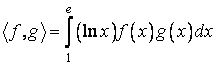 .
.
a) Sa se arate ca aplicatia defineste un produs
scalar pe ![]() ;
;
b) Sa se calculeze unghiul dintre ![]() si
si ![]() ;
;
c) Sa se calculeze ![]() pentru
pentru ![]() ;
;
d) Sa se determine o
functie ![]() care sa fie
ortogonala functiei constante
care sa fie
ortogonala functiei constante ![]() în spatiul euclidian
considerat.
în spatiul euclidian
considerat.
PP.VI.2.4.5 Fie spatiul euclidian canonic ![]() . Sa se gaseasca o baza ortonormata
pentru subspatiul generat de vectorii:
. Sa se gaseasca o baza ortonormata
pentru subspatiul generat de vectorii:
a) ![]() ;
;
b) ![]() .
.
PP.VI.2.4.6 Fie forma patratica ![]() definita prin:
definita prin: ![]() .
.
Sa se reduca la axele principale prin metoda transformarilor ortogonale si sa se gaseasca directiile principale si formulele de schimbare a coordonatelor.
L.VI.2.5 TEST DE AUTOEVALUARE
TAev.VI.2.5.1 a) Fie ![]() si
si ![]() doi vectori oarecare
din spatiul vectorial real
doi vectori oarecare
din spatiul vectorial real ![]() . Sa se arate ca aplicatia definita prin
. Sa se arate ca aplicatia definita prin 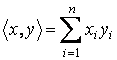 este un produs scalar
pe
este un produs scalar
pe ![]() ;
;
b) Fie ![]() si
si ![]() doi vectori oarecare
din spatiul vectorial
doi vectori oarecare
din spatiul vectorial ![]() . Sa se arate ca aplicatia definita prin
. Sa se arate ca aplicatia definita prin 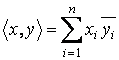 este un produs scalar
pe
este un produs scalar
pe ![]() ;
;
c) Sa se arate ca spatiul
vectorial complex al functiilor cu valori complexe, continue pe un
interval ![]() , este un spatiu euclidian complex în raport cu
aplicatia definita prin:
, este un spatiu euclidian complex în raport cu
aplicatia definita prin: 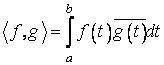 .
.
TAev.VI.2.5.2 Sa se descompuna vectorul ![]() din spatiul
euclidian
din spatiul
euclidian ![]() în suma a doi vectori:
în suma a doi vectori:
![]() , unde
, unde ![]() , cu
, cu ![]() .
.
TAev.VI.2.5.3 Sa se adauge matricei
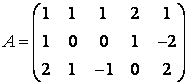
înca doua linii ortogonale între ele si cu primele trei linii.
TAev.VI.2.5.4 Sa se
arate ca subspatiile ![]() si
si ![]() din
din ![]() , unde
, unde ![]() ,
, ![]() si respectiv
si respectiv ![]() ,
, ![]() , sunt ortogonale.
, sunt ortogonale.
TAev.VI.2.5.5 Fie ![]() spatiul vectorial
real al functiilor polinomiale reale de grad cel mult
spatiul vectorial
real al functiilor polinomiale reale de grad cel mult ![]() si
si 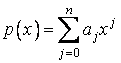 si
si 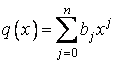 doi vectori din
doi vectori din ![]() .
.
a) Sa se arate ca aplicatiile:
(1) ![]() ,
, 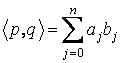 si
si
(2) ![]() ,
, 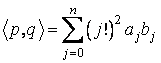
sunt produse scalare pe ![]() ;
;
b) Sa se stabileasca marimea
unghiurilor ![]() si
si ![]() , unde
, unde ![]() , utilizând produsul scalar (1);
, utilizând produsul scalar (1);
c) Sa se arate ca sistemul de
functii 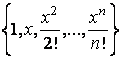 formeaza o
baza ortonormata fata de produsul scalar (2).
formeaza o
baza ortonormata fata de produsul scalar (2).
TAev.VI.2.5.6 Fie forma biliniara ![]() definita prin:
definita prin:
![]()
si
operatorul ![]() care are în baza
canonica matricea:
care are în baza
canonica matricea:
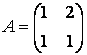 .
.
Sa se arate ca:
a)
![]() este produs scalar;
este produs scalar;
b)
![]() este autoadjunct
este autoadjunct ![]() .
.
M.VI TEMĂ DE CONTROL
TC.VI.1 Fie ![]() urmatoarele
matrice din
urmatoarele
matrice din ![]() :
:
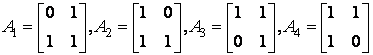 .
.
a)
Sa se gaseasca o forma liniara ![]() pe
pe ![]() astfel încât:
astfel încât:
![]() ;
;
b) Sa se determine
multimea ![]() , dimensiunea si o baza a acestui subspatiu.
, dimensiunea si o baza a acestui subspatiu.
TC.VI.2 Se da forma
biliniara ![]() :
: ![]()
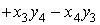 .
.
Sa se
scrie sub forma matriceala si sa se gaseasca
matricea corespunzatoare formei biliniare în raport cu baza: ![]() , unde:
, unde: 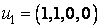 ,
, ![]() ,
, ![]() ,
, ![]() .
.
TC.VI.3 Se da forma patratica: ![]() :
: ![]() . Sa se scrie sub forma matriceala, sa se
aduca la expresia canonica prin metoda lui Gauss, metoda lui Jacobi
si respectiv prin metoda valorilor proprii, sa se stabileasca
matricea de trecere în fiecare caz si sa se verifice teorema de
inertie.
. Sa se scrie sub forma matriceala, sa se
aduca la expresia canonica prin metoda lui Gauss, metoda lui Jacobi
si respectiv prin metoda valorilor proprii, sa se stabileasca
matricea de trecere în fiecare caz si sa se verifice teorema de
inertie.
TC.VI.4 Fie aplicatia ![]() , definita prin:
, definita prin: ![]() ,unde
,unde ![]() si
si ![]() ,
, ![]() , unde
, unde ![]() .
.
a)
Sa se determine a si b astfel încât aplicatia ![]() sa fie o
forma biliniara simetrica de rang 2 în raport cu baza
canonica din
sa fie o
forma biliniara simetrica de rang 2 în raport cu baza
canonica din ![]() ;
;
b)
Pentru a si b astfel determinati sa se gaseasca matricea
formei ![]() , în raport cu baza
, în raport cu baza ![]() , unde:
, unde: ![]() ;
;
c)
Sa se gaseasca o baza ![]() în
în ![]() în care matricea
lui
în care matricea
lui ![]() sa fie matrice
diagonala, iar
sa fie matrice
diagonala, iar ![]() sa aiba
forma canonica;
sa aiba
forma canonica;
d) Sa se exprime ![]() în baza duala
în baza duala ![]() .
.
TC.VI.5 Sa se
demonstreze ca orice matrice pozitiv definita ![]() admite o descompunere
triunghiulara, adica exista o matrice superior
triunghiulara
admite o descompunere
triunghiulara, adica exista o matrice superior
triunghiulara ![]() astfel încât
astfel încât ![]() se poate reprezenta
sub forma produsului:
se poate reprezenta
sub forma produsului: ![]() . Sa se deduca aceasta descompunere pentru
matricea atasata fiecareia dintre formele patratice:
. Sa se deduca aceasta descompunere pentru
matricea atasata fiecareia dintre formele patratice:
1) ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3)![]() ,
, ![]() ;
;
TC.VI.6 Sa se arate ca în spatiul real al functiilor cu
valori reale, continue pe un interval ![]() , aplicatia definita prin:
, aplicatia definita prin: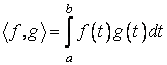 este un produs scalar care induce o structura de
spatiu euclidian.
este un produs scalar care induce o structura de
spatiu euclidian.
TC.VI.7 Fie ![]() spatiul vectorial
real al sirurilor de numere reale
spatiul vectorial
real al sirurilor de numere reale ![]() pentru care seria
pentru care seria ![]() este convergenta.
Fie
este convergenta.
Fie ![]() si
si ![]() doua elemente din
doua elemente din
![]() .
.
a) Sa se arate ca seria 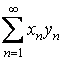 este absolut
convergenta;
este absolut
convergenta;
b) Sa se verifice ca aplicatia definita prin 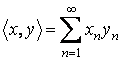 este un produs scalar
pe
este un produs scalar
pe ![]() ;
;
c) Sa se calculeze ![]() pentru
pentru ![]() si sa se
determine
si sa se
determine ![]() stiind ca
stiind ca 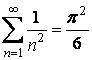 ;
;
d) Sa se arate ca sirul cu termenul general ![]() apartine
exteriorului sferei cu centrul în origine, de raza
apartine
exteriorului sferei cu centrul în origine, de raza ![]() si bilei deschise
cu centrul în origine, de raza
si bilei deschise
cu centrul în origine, de raza ![]() .
.
TC.VI.8 Fie ![]() spatiul vectorial
euclidian canonic al al functiilor reale, continue, definite pe
spatiul vectorial
euclidian canonic al al functiilor reale, continue, definite pe ![]() , înzestrat cu produsul scalar definit prin:
, înzestrat cu produsul scalar definit prin: 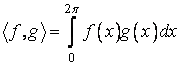 .
.
a) Sa se verifice ca multimea ![]() , unde
, unde ![]() este liniar
independenta si sa se ortonormeze;
este liniar
independenta si sa se ortonormeze;
b) Fie ![]() subspatiul de
dimensiune
subspatiul de
dimensiune ![]() generat de vectorii:
generat de vectorii: ![]() (spatiul
vectorial al polinoamelor trigonometrice), sa se expliciteze
proiectia lui
(spatiul
vectorial al polinoamelor trigonometrice), sa se expliciteze
proiectia lui ![]() pe
pe ![]() , unde
, unde ![]() .
.
TC.VI.9 Se dau formele patratice:
![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() .
.
Sa se arate ca
formele biliniare simetrice atasate celor doua forme patratice, ![]() si respectiv
si respectiv ![]() , sunt produse scalare pe
, sunt produse scalare pe ![]() si pentru fiecare
sa se gaseasca câte o baza ortonormata în raport cu
produsul scalar respectiv.
si pentru fiecare
sa se gaseasca câte o baza ortonormata în raport cu
produsul scalar respectiv.
TC.VI.10 Ecuatia carteziana a unei
suprafete din ![]() este:
este:
![]() .
.
Sa se stabileasca natura suprafetei, ecuatia sa redusa la axele principale, directiile axelor principale în care suprafata este redusa la forma canonica si formulele de schimbare a coordonatelor.
TC.VI.11 Fie
![]() un operator liniar a
carei matrice asociata în baza canonica a lui
un operator liniar a
carei matrice asociata în baza canonica a lui ![]() este
este ![]() , unde
, unde ![]() este matricea unitate
de ordinul
este matricea unitate
de ordinul ![]() , iar
, iar ![]() este matricea de
ordinul
este matricea de
ordinul ![]() cu toate elementele
egale cu 1.
cu toate elementele
egale cu 1.
a) Sa se calculeze valorile proprii ale operatorului ![]() ;
;
b) Pentru ![]() sa se reduca
forma patratica
sa se reduca
forma patratica ![]() , la forma canonica prin metoda transformarilor
ortogonale si sa se precizeze transformarea ortogonala
corespunzatoare.
, la forma canonica prin metoda transformarilor
ortogonale si sa se precizeze transformarea ortogonala
corespunzatoare.
TC.VI.12 Fie formele patratice:
![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() .
.
Sa se reduca la forma canonica prin metoda transformarilor ortogonale si sa se precizeze baza în care s-a obtinut forma canonica, directiile axelor principale, transformarea ortogonala corespunzatoare si formulele de schimbare a coordonatelor.
Bibliografie
Udriste C., s.a., -Probleme de algebra, geometrie si ecuatii diferentiale, Editura Didactica si Pedagogica, Bucuresti, 1981.
Udriste C., -Aplicatii de algebra, geometrie si ecuatii diferentiale, Editura Didactica si Pedagogica, Bucuresti, 1993.
Ion D.I., R. Nicolae, -Algebra, Editura Didactica si Pedagogica, Bucuresti, 1982.
Flondor D., N. Donciu, -Algebra si analiza matematica-culegere de probleme, vol I, Editura Didactica si Pedagogica, Bucuresti, 1978.
Otlacan E., s.a. -Algebra superioara-îndrumar teoretic si culegere de probleme, Editura Academiei Tehnice Militare, Bucuresti, 1995.
Mânzatu E., Gârban V. -Algebra cu aplicatii rezolvate la calculatorul electronic, Editura Academiei Militare, Bucuresti, 1982.
|