SUBIECTE PENTRU EXAMENUL
ANALIZĂ MATEMATICĂ II
(CALCUL INTEGRAL)
PROFESOR PAUL FLONDOR
Din cauza faptului ca numeroase subiecte se repetau la diferite versiuni ale examenului, exercitiile si problemele au fost grupate pe capitole, modul de combinare al acestora urmând a fi explicat la sfârsitul lucrarii.
Continuitatea si derivabilitatea integralelor improprii cu parametru.
Lungimea drumului.
Independenta integralei curbilinii de drum.
Teorema lui Poincaré pentru C2.
Teorema de convergenta monotona.
Teorema de convergenta dominanta.
2.1) Inegalitatea lui Cebâsev. Legea numerelor mari. Aplicatia Benoulli.
2.2) Lema lui Foton.
2.3) Legi de probabilitate uniforma, Poisson, Gauss si sa se defineasca densitatea de probabilitate, functia de repartitie si dispersia.
3.1) Formula integrala Cauchy si aplicatii la dezvoltarea în serie a functiilor olomorfe.
3.2) Teorema Cauchy (enunt, demonstratie) si formula integrala Cauchy.
3.3) Inegalitatile lui Cauchy, teorema lui Liouville si teorema fundamentala a algebrei.
II. INTEGRALE CU PARAMETRU (FUNCŢII DEFINITE DE INTEGRALE)
Sa se calculeze valoarea urmatoarelor integrale cu parametru
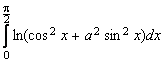
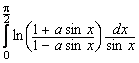 ,
, ![]()
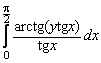
Pornind
de la valoarea integralei  sa
se determine valoarea integralei
sa
se determine valoarea integralei

III. INTEGRALE CURBILINII sI FORMULA LUI STOKES
Sa
se calculeze ![]() unde
unde
![]() reprezinta intersectia planului
reprezinta intersectia planului ![]() cu cubul
cu cubul
![]() direct si cu
formula lui Stokes.
direct si cu
formula lui Stokes.
Sa
se calculeze ![]() unde
unde
![]() este conturul
este conturul ![]() cu
cu ![]() ,
, ![]() si
si
![]() cu
cu ![]() , parcurs în
sensul laturilor triunghiului ABC direct si
cu Stokes.
, parcurs în
sensul laturilor triunghiului ABC direct si
cu Stokes.
Sa
se calculeze ![]() unde
unde
![]() este conturul obtinut
prin intersectia sferei
este conturul obtinut
prin intersectia sferei ![]() cu planele
cu planele ![]() ,
, ![]() si
si
![]() parcurs
în sensul invers al acelor de ceasornic daca se priveste dinspre semiaxa pozitiva Ox.
parcurs
în sensul invers al acelor de ceasornic daca se priveste dinspre semiaxa pozitiva Ox.
Sa
se calculeze ![]() , unde
, unde ![]() este
un drum de clasa C1 care uneste
un punct de pe sfera
este
un drum de clasa C1 care uneste
un punct de pe sfera ![]() cu un punct de pe
sfera
cu un punct de pe
sfera ![]() cu
cu ![]() .
.
Sa
se calculeze ![]() , unde
, unde ![]() este
un drum de clasa C1 care uneste
un punct de pe sfera
este
un drum de clasa C1 care uneste
un punct de pe sfera ![]() cu un punct de pe
sfera
cu un punct de pe
sfera ![]() cu
cu ![]() .
.
Sa
se calculeze ![]() , unde
, unde 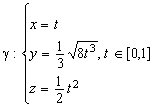
Sa se calculeze
![]() , unde
, unde 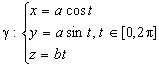
![]() , unde
, unde ![]() reprezinta
intersectia suprafetelor
reprezinta
intersectia suprafetelor
![]() si
si
![]() cu
cu ![]() .
.
Sa se studieze exactitatea formelor si sa se calculeze o primitiva (acolo unde este posibil) :
a)
![]() pe
pe
![]() ;
;
b)
![]() , cu
, cu ![]() ;
;
c)
Sa
se studieze independenta
de drum a integralei 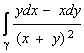 .
.
Sa se calculeze lungimile arcelor :
a)
![]() unde
unde ![]() , unde
, unde ![]() este
un numar real.
este
un numar real.
b)
![]() unde
unde
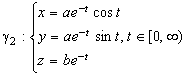
INTEGRALE EULERIENE
Sa
se calculeze 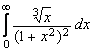 .
.
Sa
se calculeze 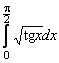 .
.
IV. INTEGRALE DUBLE sI ARII
Sa se calculeze ariile marginite de curbele

![]()
![]() ,
, ![]() ,
, ![]() si
si
![]() cu
cu ![]() si
si
![]()
Sa
se calculeze ![]() unde
D este domeniul marginit de curbele
unde
D este domeniul marginit de curbele ![]() ,
, ![]() ,
, ![]() si
si
![]() .
.
V. INTEGRALE TRIPLE sI VOLUME
Sa se calculeze urmatoarele integrale triple :
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Sa se calculeze volumele marginite de suprafetele

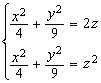
![]()
![]()
![]()
![]()
![]()
Sa se calculeze volumul delimitat de 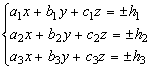 stiind
ca determinantul
stiind
ca determinantul  .
.
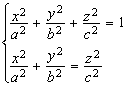
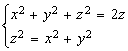
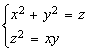
VI. INTEGRALE DE SUPRAFAŢĂ sI FORMULA GAUSS-OSTROGRADSKI
Sa
se calculeze aria decupata
de suprafata ![]() din suprafata
din suprafata ![]() .
.
Sa
se calculeze aria decupata
de suprafata ![]() din suprafata
din suprafata ![]() , cu
, cu ![]() .
.
Sa
se calculeze aria decupata
de suprafata ![]() din suprafata
din suprafata ![]() .
.
Sa
se calculeze aria suprafetei ![]() .
.
![]() , unde
, unde ![]() .
.
Fie câmpurile vectoriale ![]() si
si ![]() , unde
, unde ![]() este
un vector constant, iar
este
un vector constant, iar ![]() este
vectorul de pozitie. Sa
se calculeze acestor câmpuri pe fata
interioara a unei sfere centrate în origine
si de raza R si fluxurile pe fata
exterioara a sferei
din care se elimina originea.
este
vectorul de pozitie. Sa
se calculeze acestor câmpuri pe fata
interioara a unei sfere centrate în origine
si de raza R si fluxurile pe fata
exterioara a sferei
din care se elimina originea.
Se da câmpul vectorial ![]() si
piramida determinata de
si
piramida determinata de ![]() ,
, ![]() ,
, ![]() si
si
![]() . Sa se calculeze
fluxul câmpului
. Sa se calculeze
fluxul câmpului ![]() prin
suprafata piramidei
direct si cu Gauss-Ostrogradski.
prin
suprafata piramidei
direct si cu Gauss-Ostrogradski.
VII. ELEMENTE DE PROBABILISTICĂ
O variabila x are densitatea de repartitie având graficul ca în figura
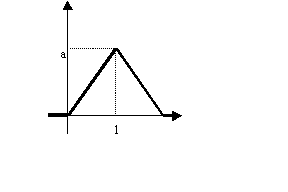
Se
cere sa se calculeze media, dispersia si probabilitatile ![]()
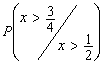 .
.
Fie
x o varaiabila repartizata
uniform în intervalul [-1 ]. Sa se calculeze
densitatea si repartitia lui ![]() .
.
Fie
x o variabila aleatoare
uniform distribuita. Se cere
sa se calculeze dispersia si densitatea lui ![]() .
.
sirul
de variabile aleatoare ![]() îndeplineste
conditia
îndeplineste
conditia 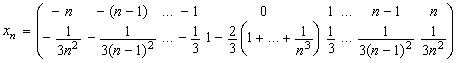
a) Sa se calculeze media si dispersia fiecareia;
b) Sa se stabileasca daca sirul verifica legea numerelor mari (Cebâsev).
Un sir de variabile aleatoare independente ![]() , ia valorile
, ia valorile ![]() si
si
![]() ,
, 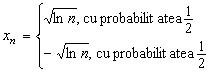 . Sa se stabileasca daca
sirul satisface legea numerelor mari a lui
Cebâsev.
. Sa se stabileasca daca
sirul satisface legea numerelor mari a lui
Cebâsev.
Sa
se calculeze masa lantisorului ![]() ,
, ![]() , daca densitatea de-a lungul arcului este egala cu patratul abscisei
, daca densitatea de-a lungul arcului este egala cu patratul abscisei ![]() .
.
VIII. ELEMENTE DE ANALIZĂ COMPLEXĂ
Sa se precizeze câte determinari are fiecare din expresiile urmatoare si sa se afle valoarea expresiei în determinarea principala :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() .
.
Sa
se demonstreze ca ![]() si
si
![]() sunt
simultan olomorfe, adica domeniul este invariant la conjugare.
sunt
simultan olomorfe, adica domeniul este invariant la conjugare.
Sa se dezvolte
în serie de puteri (
![]() în coroana circulara
în coroana circulara ![]() .
.
![]() în jurul punctelor
în jurul punctelor ![]() ,
, ![]() ,
, ![]() si
si
![]() .
.
![]() în jurul punctului
în jurul punctului ![]() .
.
![]() în coroana circulara
în coroana circulara ![]() .
.
![]() în jurul punctului
în jurul punctului ![]() .
.
Sa se calculeze urmatoarele integrale în domeniul complex :
![]() unde
unde ![]() este
un arc orientat parcurs o singura data.
este
un arc orientat parcurs o singura data.
![]() unde
unde ![]() este
o curba închisa orientata trigonometric, iar
este
o curba închisa orientata trigonometric, iar
![]() .
.
Se
da ![]() . Sa se dezvolte
în serie functia f în jurul punctului
. Sa se dezvolte
în serie functia f în jurul punctului ![]() .
.
Exista o functie f olomorfa în vecinatatea punctului ![]() , care sa ia în punctele
, care sa ia în punctele ![]() valorile
:
valorile
:
a) . ?
b)
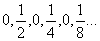 ?
?
c)
![]() ?
?
Exista o functie f analitica în vecinatatea punctului ![]() astfel
încât
astfel
încât ![]() începând
cu o valoare a lui n ?
începând
cu o valoare a lui n ?
Exista o functie întreaga f astfel încât sa existe
![]() si
si
![]() astfel încât
astfel încât ![]() ,
, ![]() ? Sa
se demonstreze ca f este
un polinom de grad maxim p.
? Sa
se demonstreze ca f este
un polinom de grad maxim p.
Exista o functie f într-o vecinatate a punctului ![]() astfel
încât
astfel
încât ![]() ,
, ![]() ?
?
Sa se calculeze urmatoarele integrale folosind teorema reziduurilor
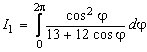
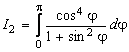
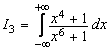
|