In acest capitol sunt tratate criteriile care arata când o descompunere a unei relatii determinata de o schema a unei baze de date este o reprezentare adecvata. Se introduce echivalenta prin date a schemelor bazelor de date. Aceste criterii sunt date la început pentru o multime arbitrara de relatii P, apoi se formuleaza rezultate suplimentare pentru cazul P=SAT(C).
9.1 Reprezentare adecvata
Vom introduce câteva notatii care vor fi folosite sistematic pe parcursul acestui capitol. Scopul este de a construi o reprezentare adecvata a elementelor multimii de relatii P. relatiile din P vor fi relatii de schema U.
Relatiile din Q le vom numi stari posibile (instantieri) pentru a le deosebi de relatiile care compun baza de date. Schema bazei de date va fi notata cu, R= unde U=R1R2.Rp. Multimea bazelor de date de schema R va fi notata cu D. Se pune problema reprezentarii instantelor din P prin baze de date din D si examinarea restrictiilor impuse schemei bazei de date pentru ca aceste reprezentari sa fie adecvate.
Definitia 9.1. Se numeste proiectie (transformare de proiectie) definita de schema R, notata pR transformarea care face sa corespunda unei instante r Q o baza de date d D, adica pR=d, unde d= si pRi ri 1≤i≤p.
Definitia 9.2. Transformarea care face sa corespunda unei baze
de date d D o instanta din Q si
este notata cu ![]() se numeste transformare de unire definita
de R. Pentru baza de date d= D d=r1 r2 rp.
se numeste transformare de unire definita
de R. Pentru baza de date d= D d=r1 r2 rp.
Descrierea schemei este implicita în structura bazei de date d.
Exemplul 9.1. Fie ![]() si
si ![]() Daca r este instanta
din figura 1, baza de date este
Daca r este instanta
din figura 1, baza de date este ![]()
![]() , unde
, unde ![]() si
si ![]() sunt în figura 2 ; iar instanta s=
sunt în figura 2 ; iar instanta s=![]() d este data în figura 3.
d este data în figura 3.
r(A B C) ![]() =
=![]() (A B )
(A B ) ![]() (B C) s(A B C)
(B C) s(A B C) ![]() '(B C)
'(B C)
3 5 1 3 3 5 1 3 5 9 8
1 4 6 1 4 4 6 1 4 5 3 9
2 4 5 2 4 4 5 1 4 6
2 4 6 2 4 5
2 4 6
Figura 1 Figura 2 Figura 3 Figura 4
Daca
se considera în locul relatiei ![]() relatia
relatia ![]() ' atunci
' atunci ![]() d= , adica instanta vida pe U.
d= , adica instanta vida pe U.
Definitia9.3. Fie P Q. Se numeste imagine directa a lui P determinata
de R, notata cu ![]() multimea: pR(P)=.
multimea: pR(P)=.
Pentru usurinta scrierii vom renunta la p. Din definitia transformarii de proiectie
rezulta ca pP pQ D. Ultima incluziune este stricta
deoarece nu orice baza de date este
proiectia unei stari
admisibile oarecare din Q. Baza de date ![]() unde
unde ![]() este dat în figura 1 iar
este dat în figura 1 iar ![]() este dat in figura 4, nu este proiectia
nici unei instante cu schema ABC.
Vom considera ca numai bazele de date din pQ pot candida pentru a reprezenta
cu ele instante din P. Multimea
pQ se compune din acele baze de date de schema R care se pot uni complet. In legatura
cu aceasta, se pun urmatoarele întrebari:
este dat in figura 4, nu este proiectia
nici unei instante cu schema ABC.
Vom considera ca numai bazele de date din pQ pot candida pentru a reprezenta
cu ele instante din P. Multimea
pQ se compune din acele baze de date de schema R care se pot uni complet. In legatura
cu aceasta, se pun urmatoarele întrebari:
sa se decida daca o multime de relatii se pot uni complet ?
bazele de date care nu se pot uni complet pot fi semnificative ?
sa se verifice daca o baza de date din pQ trebuie considerata în întregime ? Nu este
suficient sa consideram perechi de relatii în baze de date sau relatii individuale ?
Exemplu 9.2. Fie relatiile r1, r2 si r3 din figura 5.
r1 (A B) r2 (B C) r3 (A C)
2 3 3 6 2 8
4 5 5 8 4 6
Acestea se pot uni complet daca le luam ca perechi, însa toate trei împreuna nu pot fi unite. In continuare sunt prezentate restrictiile impuse relatiilor care compun baza de date derivata din Q de înlaturare a acestor contradictii.
CWR(P)=, ri pRi(P)}
se numeste imagine pe componente a lui P determinata de R
Adica CWR(P) consta din baze de date de schema R ale caror relatii sunt proiectii de instante din P dar nu în mod necesar ale aceleiasi instante. E clar ca pP CWR(P) care în cele mai multe cazuri este stricta. Pentru reprezentarea lui P trebuie utilizate numai acele baze de date care sunt proiectii de instante pentru care imaginile pe componente sunt proiectii de instante din Q. Multimea acestor baze de date o vom nota cu L. Ea este data de: L= CWR(P)∩pQ. Este clar ca pP L si pP pQ
Relatiile de incluziune între multimile introduse la momentul actual sunt aratate in figura 6.
pQ

 P D
P D
![]()

![]()
 Q
Q
![]()
![]()
 pP
pP
![]()
![]()
![]()
 P
P
![]()
![]()
Figura 6 L
Definitia 9.5. Daca
N D atunci N= ![]() .
.
Notiunea de reprezentare adecvata a fost introdusa de Rissanen / /.
Definitia 9.6. Schema bazei de date R descompune relatiile din P în componente independente daca au loc urmatoarele doua proprietati:
IC1: Daca d L atunci exista cel mult o instanta r P cu pr=d.
IC2: Daca d L atunci exista cel putin o instanta r P cu pr=d.
Proprietatea IC1 se numeste proprietate de reprezentare unica. Proprietatile IC1 si IC2 împreuna constituie conditia de componente independente. Conditia de componente independente impune ca transformarea p : P L sa fie bijectiva.
Se
poate transcrie IC1 si IC2 ca o singura conditie, dar cum în
continuare IC1 se va folosi în alte determinari ale adecvarii, le-am
formulat separat. Observam ca
IC2 este adevarata daca si
numai daca pP=L. Conditia de componente independente
provoaca greutati când vrem sa revenim de la baza de date
la instanta caci transformarea inversa a lui p e greu de calculat. Conditiile IC1 si IC2 nu cer ca ![]() sa fie inversa lui p. Este foarte posibila situatia reprezentata
în figura 7.
sa fie inversa lui p. Este foarte posibila situatia reprezentata
în figura 7.

 Q pQ
Q pQ
![]()
![]()

![]() P p L pP
P p L pP
![]()
![]() p
p
![]()
![]()
Figura 7
Exemplul 9.3. Fie: U=ABC, R=.
P se compune din asemenea stari admisibile ce satisfac
urmatoarea conditie: pentru orice pereche de tupluri ![]() si
si ![]() din r
din r ![]() determina
determina ![]()
Unirea unei baze de date din pQ poate sa nu fie o instanta din P.
Urmatoarea notiune de adecvare a fost introdusa de Arora si Carlson / /.
Definitia 9.7. Schema bazei de date R descrie o descompunere care conserva informatiile din P daca ea are urmatoarele proprietati:
AC1. Pentru d L exista cel mult o instanta r P astfel ca p(r)=d;
AC2. Daca instanta r Q este proiectata în L, adica p(r) L rezulta atunci ca r P.
Proprietatea AC2 se numeste restrictie de conservare. AC1 si AC2 constituie o conditie de conservare a informatiei.
Definitia 9.8. Pentru orice submultime N pQ se numeste preimagine a lui N, notata N , multimea : N
Multimea
care ne intereseaza este![]() . Relatia
dintre
. Relatia
dintre ![]() si alte multimi este aratata în figura urmatoare
si alte multimi este aratata în figura urmatoare
D pQ

![]()
![]()
![]()
 Q
Q
![]()
![]()


![]()
![]() L
L
![]()
![]()
![]()
![]() P
P
![]() pP
pP
Figura 8
Lema 9.1. AC2 este echivalenta cu proprietatea ![]()
Demostratie Presupunem
ca are loc AC2. Pentru orice ![]() , p(r) L, atunci
din AC2 rezulta ca r P deci
, p(r) L, atunci
din AC2 rezulta ca r P deci ![]() . Deoarece
. Deoarece ![]() , rezulta ca
, rezulta ca
![]() .
.
Presupunem ca ![]() . Pentru orice instanta
. Pentru orice instanta ![]() , unde p(r) L rezuLta ca r P. Deci AC2 este satisfacuta.
, unde p(r) L rezuLta ca r P. Deci AC2 este satisfacuta.
Observatie. ![]() determina L=pP. Din aceasta rezulta consecinta care leaga
conditia de componente independente de conditia de conservare a
informatiei.
determina L=pP. Din aceasta rezulta consecinta care leaga
conditia de componente independente de conditia de conservare a
informatiei.
Corolar 9.1. AC2 implica IC2, prin urmare AC1 si AC2 implica IC1 si IC2.
Observatie. In sens invers implicatia nu este adevarata.
Din proprietatile AC1 si AC2 rezulta ca, putem reprezenta orice instanta r P printr-o baza de date d L si de asemenea rezulta ca d nu este posibil sa reprezinte o alta instanta din Q-P. Conditia de conservare a informatiei specifica faptul ca exista inversa transformarii p
Observatie.
Intotdeauna ![]()
Lema 9.2. Proprietatea LJ implica proprietatea IC1.
Demonstratie. Presupunem ca LJ are loc. Fie instantele ![]() . Daca
. Daca ![]() . Din proprietatea LJ rezulta r=
. Din proprietatea LJ rezulta r=![]() p(r)). Prin urmare IC1 este corecta.
p(r)). Prin urmare IC1 este corecta.
Corolar9.2. LJ si AC2 implica AC1 si AC2.
Lema 9.3. Proprietatile AC1 si AC2 implica LJ.
Demonstratie. Presupunem ca sunt îndeplinite conditiile de
conservare a informatiei. Fie ![]() si d=p(r). Aratam
ca
si d=p(r). Aratam
ca![]() (d) este de
asemenea o instanta astfel ca
(d) este de
asemenea o instanta astfel ca ![]() Deoarece d L din AC2 rezulta ca
Deoarece d L din AC2 rezulta ca![]() (d) P. AC1 implica
(d) P. AC1 implica![]() (d) =r deoarece p(r)= =p
(d) =r deoarece p(r)= =p ![]() (d) Prin urmare r=
(d) Prin urmare r=![]() (d)
(d) ![]() care este proprietatea LJ.
care este proprietatea LJ.
Teorema 9.1. Daca AC2 este adevarata atunci proprietatile AC1 si LJ sunt echivalente.
Adica
în conditiile de conservare a informatiei ![]() este inversa lui p pe P.
este inversa lui p pe P.
Exemplul 9.4. Fie ![]() F-dependenta
F-dependenta ![]() asigura ca proprietatea LJ are loc. Daca
instanta r satisface
asigura ca proprietatea LJ are loc. Daca
instanta r satisface ![]() atunci
atunci ![]() satisface
satisface ![]() . Invers,
. Invers, ![]() satisface
satisface ![]() , atunci r va satisface
, atunci r va satisface ![]() . De aceea daca
. De aceea daca ![]() pentru instanta r, atunci
pentru instanta r, atunci ![]() . Multimea P satisface
proprietatea AC2, deci este indeplinita
conditia de consevare a informatiei.
. Multimea P satisface
proprietatea AC2, deci este indeplinita
conditia de consevare a informatiei.
Dupa cum am observat chiar în conditiile îndeplinirii proprietatilor IC1 sI IC2 transformarea inversa de la baza de date la instante poate sa nu fie usor de calculat. Am vazut ca din proprietatile AC1 sI AC2 rezulta ca aplicatia de unire este inversabila dar pentru aceasta trebuie sa verificam ca p(r) nu apartine lui L pentru r Q-P. Vom prezenta o conditie intermediara între conditia de componente independente si conditia de conservare.
Definitia 9.10. Vom spune ca schema bazei de date R satisface conditia de unire (join) pe P daca au loc urmatoarele proprietati :
J1) Aceeasi ca IC1;
J2) Pentru orice baza de date d L, ![]() d P.
d P.
Observatie
: J1 si J2 cer ca ![]() sa fie transformare inversa a lui p pe P.
sa fie transformare inversa a lui p pe P.
Daca
r P atunci p(r) L. Din J2 rezulta mR(r) P dar p(mR(r))=p(r), iar din J1 mR(r)=r. Vom arata ca
proprietatea LJ are loc pe multimea P.
Conditia de unire atrage dupa sine ca, orice baza de date d L poate fi reprezentata printr-o instanta
maximala r P astfel ca ![]() d=r
d=r
Lema 9.4. Proprietatea J2 are loc daca si numai daca FIX(R) L P.
Demonstratie Necesitatea.
J2 poate fi scrisa ca ![]() L P.
L P.
Fie r FIX(R) L . Deoarece r L rezulta
ca p(r) L si r FIX(R), r=![]() p(r) astfel ca r
p(r) astfel ca r ![]() L. Prin
urmare r P, deci FIX(R)
L P.
L. Prin
urmare r P, deci FIX(R)
L P.
Suficienta.
Presupunem ca FIX(R) L P si ca
r este o instanta r ![]() L, atunci
exista o baza de date d L asfel încât
r=
L, atunci
exista o baza de date d L asfel încât
r=![]() d. Deoarece FIX(R) L P atunci d=p(r), mR(r)=
d. Deoarece FIX(R) L P atunci d=p(r), mR(r)= ![]() p(r)=
p(r)= ![]() d FIX(R). Prin
urmare r FIX(R), deoarece d L atunci r L Din ipoteza ca
r P rezulta ca
d FIX(R). Prin
urmare r FIX(R), deoarece d L atunci r L Din ipoteza ca
r P rezulta ca ![]() L P.
L P.
Comparam conditiile de componente independente cu conditiile de conservare a informatiei.
Lema 9.5. Din proprietatea J2 rezulta IC2
Demonstratie Presupunem J2 adevarata, adica![]() L P atunci pentru orice d L exista r P astfel încât
L P atunci pentru orice d L exista r P astfel încât ![]() d=r.
d=r.
![]()
![]()
 s p
s p
s' ![]()
![]()
![]()
![]()
r' p
Figura 9
![]()
P ![]()
r
Teorema 9.2. Din proprietatile AC1 si AC2 rezulta J1 si J2, din care la rândul lor
rezulta IC1 si IC2.
Demonstratie. Presupunem
ca AC1 si AC2 sunt îndeplinite. Atunci J1 este adevarata.
Pentru a dovedi ca J2 este adevarata vom lua o instanta
arbitrara r ![]() L. Fie
L. Fie ![]() atunci din AC2 rezulta
ca r P prin
urmare
atunci din AC2 rezulta
ca r P prin
urmare ![]() L P deci J2 este îndeplinita. Restul implicatiilor
rezulta din lema 5. Atunci când se
compara AC1 si AC2 cu J1 si J2 se observa ca toate cer
realizarea conditiei LJ
L P deci J2 este îndeplinita. Restul implicatiilor
rezulta din lema 5. Atunci când se
compara AC1 si AC2 cu J1 si J2 se observa ca toate cer
realizarea conditiei LJ ![]() , iar AC2 impune
, iar AC2 impune ![]() în timp ce din
J1 si J2 rezulta ca P
este o submultime proprie a lui L
în timp ce din
J1 si J2 rezulta ca P
este o submultime proprie a lui L
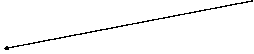
}i în ambele conditii nu pot sa existe r si r' aratata în figura 9 dar pot sa existe s si s' dar nu pot satisface conditiile AC1 si AC2.
Exemplul 9.5. Fie ![]() . Atunci L se compune din doua perechi de relatii care se unesc
complet pe AB si BC si
. Atunci L se compune din doua perechi de relatii care se unesc
complet pe AB si BC si ![]() este reformularea lui
este reformularea lui ![]() astfel ca R satisface LJ si deci J1. Reuniunea a doua relatii cu schema
AB si BC satisface
astfel ca R satisface LJ si deci J1. Reuniunea a doua relatii cu schema
AB si BC satisface ![]() rezulta ca J2 e adevarat. AC2 nu se satisface deoarece orice instanta
r satisface p(r) L rezulta P Q. Este posibil ca r P astfel încât
rezulta ca J2 e adevarat. AC2 nu se satisface deoarece orice instanta
r satisface p(r) L rezulta P Q. Este posibil ca r P astfel încât ![]()
Definitia 9.11. Schema bazei de date R conserva (pastreaza) P daca are loc proprietatea :
PR. Pentru orice instanta r P atunci mR(r) P adica mR(P) P unde mR(P) = ![]() p(P).
p(P).
Lema 9.6. Proprietatea J2 implica proprietatea PR. Invers nu e adevarat.
Demonstratie. Din ![]() L=P rezulta ca pentru orice r P avem mR(r) P.
L=P rezulta ca pentru orice r P avem mR(r) P.
Exemplul 9.6. Fie U=ABC, R= P=SAT(A »B,B »A)
Fie P SAT(B »A) , atunci ![]() , adica PR e adevarata. Sa examinam baza de date
, adica PR e adevarata. Sa examinam baza de date ![]() unde relatiile
unde relatiile ![]() si
si ![]() sunt prezentate în fig. 10. Baza de date d este în L deoarece
sunt prezentate în fig. 10. Baza de date d este în L deoarece ![]() date în fig. 11. E usor de vazut ca starea
admisibila
date în fig. 11. E usor de vazut ca starea
admisibila ![]() (d) data
în fig. 12 nu este în P astfel J2 nu e adevarat.
(d) data
în fig. 12 nu este în P astfel J2 nu e adevarat.
![]() (A B)
(A B) ![]() (B C) S (A B C) S (A B C)
(B C) S (A B C) S (A B C) ![]() (d) (A B C)
(d) (A B C)
3 5 1 3 5 1 3 5 1 3 5
1 4 3 6 1 4 5 1 3 6 1 3 6
2 4 4 5 2 4 5 2 4 5 1 4 5
4 6 2 4 6 1 4 6
4 7 2 4 7 1 4 7
2 4 5
2 4 6
2 4 7
Figura 10 Figura 11 Figura 12
Lema 9.7. Proprietatile PR si IC2 implica proprietatea J2.
Demonstratie. Fie r ![]() L si d o
baza de date din L, astfel ca
r=
L si d o
baza de date din L, astfel ca
r=![]() d, din IC2 avem pP=L astfel ca
d pP. Fie r' o instanta din P astfel ca p(r')=d. Atunci din PR rezulta
d, din IC2 avem pP=L astfel ca
d pP. Fie r' o instanta din P astfel ca p(r')=d. Atunci din PR rezulta ![]() . Prin urmare
. Prin urmare ![]() L P si J2 este adevarata.
L P si J2 este adevarata.
Corolar 9.3. Proprietatile IC1, IC2 si PR sunt îndeplinite daca si numai daca J1 si J2 sunt îndeplinite.
Observatie. Putem înlocui IC1 si PR cu LJ.
Lema 9.8. Proprietatea LJ implica proprietatea PR.
Demonstratie. Din ![]()
Teorema 9.3. Conditiile LJ si IC2 sunt adevarate daca si numai daca J1 si J2 sunt adevarate.
Demonstratie. Din lema 9.2 rezulta ca LJ implica IC1. Din lema 9.8 rezulta ca LJ implica PR. Prin urmare din corolarul teoremei 9.2 si lema 9.7 LJ si IC2 implica conditiile de unire. Din teorema 9.2 rezulta ca J1 si J2 implica IC2. Din J1 si J2 rezulta de asemenea LJ prin urmare din J1 si J2 rezulta LJ si IC2.
Vom studia acum ce fel de proprietati trebuie adaugate la conditiile de unire ca sa obtinem un sistem de conservare a informatiei.
Definitia 9.12. Schema bazei de date R satisface proprietatea S daca ![]()
Teorema 9. 4. Proprietatile J1, J2 si S au loc daca si numai daca AC1, AC2 au loc.
Demonstratie "< ". Din teorema
9.2 rezulta ca AC1 si AC2 implica J1 si J2. Din lema 9.1 proprietatea AC2 cere ca ![]() . Din lema 9.3 AC1 si AC2 implica
proprietatea LJ astfel ca P FIX(R). Prin
urmare L =P FIX(R) care
implica proprietatea S.
. Din lema 9.3 AC1 si AC2 implica
proprietatea LJ astfel ca P FIX(R). Prin
urmare L =P FIX(R) care
implica proprietatea S.
" >'. Se arata
ca J2 si S implica AC2. Fie r o instanta din L unde p(r)=d, pentru d L. Din J2 rezulta ca![]() d P. Din
d P. Din ![]() AC2 este adevarat.
AC2 este adevarat.
Diferenta între conditiile de unire si conditiile
de conservare necesita ![]() sau mai strict
sau mai strict 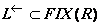 . In multe cazuri ne intereseaza situatiile
când P este descrisa de o multime de restrictii C. In acest caz
. In multe cazuri ne intereseaza situatiile
când P este descrisa de o multime de restrictii C. In acest caz ![]() este echivalenta cu
este echivalenta cu ![]() . Se cunoaste un astfel de
procedeu de verificare a conditiilor C daca acestea sunt formate din dependente functionale
si dependente multivoce. Conditia
. Se cunoaste un astfel de
procedeu de verificare a conditiilor C daca acestea sunt formate din dependente functionale
si dependente multivoce. Conditia 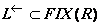 este aceeasi cu
este aceeasi cu ![]() . Unde am utilizat pC pentru proiectia restrictiilor C pe R.
. Unde am utilizat pC pentru proiectia restrictiilor C pe R.
9.2 D-echivalenta schemelor bazelor de date
Se spune despre schemele R si S ca sunt echivalente daca TR(r)=TS(r) pentru orice instanta r din P. Schemele R si S sunt echivalente pe P în cazul când transformarile TR(r) si TS(r) restrictionate la P coincid (adica când descompunerea determinata de R a starii admisibile r P are aceleasi pierderi de informatii ca si descompunerea determinata de S). Ne intereseaza doar acele instante care prin descompunere nu pierd informatii.
Definitia 9.13. Fie R o schema a unei baze de date si
P o multime de instante posibile de schema R. Se numeste multime
de puncte fixe determinata de R în P multimea : ![]()
Definitia 9.14. Schemele bazelor de date R si S
sunt d-echivalente pe P (se noteaza ![]() ) daca
) daca ![]()
Pentru verificarea d-echivalentei (echivalenta
determinata de datele din P)
trebuie demonstrate doua incluziuni. Mentionam ca
incluziunea ![]() se realizeaza atunci când
se realizeaza atunci când ![]()
Lema 9.9. Echivalenta
![]() determina
determina ![]()
Demonstratia este lasata cititorului.
Observatie: Reciproca lemei 9.8 nu este adevarata.
Exemplul 9.7 Fie U ABCD, iar R=![]() si S=
si S=![]() scheme de baze de date. Daca
P este compusa din doua
relatii r si s date în figura 1, atunci R si S sunt d-echivalente
(echivalenta determinata de datele din P). Instanta r se descompune fara pierderi fata
de R si fata de S, în timp ce s se altereaza la
descompunere. Dar TR si
TS nu sunt echivalente pe
P, deoarece s'=TR(s) nu
coincide cu s"=TR(s) (figura 2).
scheme de baze de date. Daca
P este compusa din doua
relatii r si s date în figura 1, atunci R si S sunt d-echivalente
(echivalenta determinata de datele din P). Instanta r se descompune fara pierderi fata
de R si fata de S, în timp ce s se altereaza la
descompunere. Dar TR si
TS nu sunt echivalente pe
P, deoarece s'=TR(s) nu
coincide cu s"=TR(s) (figura 2).
r (A B C D) s(A B C D) s'(A B C D) s''(A B C D)
1 3 5 7 1 3 5 7 1 3 5 7 1 3 5 7
1 3 6 8 2 3 6 7 2 3 6 7 1 3 6 7
2 4 6 8 2 4 6 8 2 4 6 7 2 3 5 7
2 3 6 8 2 3 6 7 2 4 6 8 2 4 6 8
Figura 1 Figura 2
Definitia 9.15. Fie R o schema de baza de
date. Submultimea ![]() a lui P determinata de R, se conserva
(prezerva) în P
a lui P determinata de R, se conserva
(prezerva) în P
Conditia de conservare a lui P, este 
Observatie
: ![]()
Teorema 9.5. Fie R si S doua scheme de baze de date si P o multime de instante. Presupunem ca exista o multime de instante P' care satisface conditia:
![]()
atunci ![]() are loc
are loc ![]() pentru orice
pentru orice ![]() .
.
Demonstratie. Necesitatea. Fie r instanta
arbitrara din P'. Deoarece ![]() rezulta ca
s=mR(r) este în P. Dar PJ-tranformarea este idempotenta, deci s
este în
rezulta ca
s=mR(r) este în P. Dar PJ-tranformarea este idempotenta, deci s
este în ![]() si, în consecinta
s
si, în consecinta
s ![]() . Din ipoteza s
. Din ipoteza s ![]() . Dar
. Dar ![]() , asa ca
, asa ca ![]() . Deoarece
. Deoarece ![]() atunci mS(s)=s. Combinând ambele
inegalitati rezulta
atunci mS(s)=s. Combinând ambele
inegalitati rezulta ![]() .
.
Suficienta.
Fie r o relatie din ![]() ; atunci
; atunci ![]() '. Din ipoteza
'. Din ipoteza ![]() , dar mR(r)=r
deci mS(r) r, dar si
mS(r) r deci r FIX(S) Astfel,
, dar mR(r)=r
deci mS(r) r, dar si
mS(r) r deci r FIX(S) Astfel, ![]()
Corolar 9.4. Urmatoarele trei afirmatii sunt echivalente:
1) ![]()
2) ![]() pentru K=FIXP(R);
pentru K=FIXP(R);
3) ![]() pentru K=PRESP(R);
pentru K=PRESP(R);
Demonstratia rezulta din teorema 1.
Corolarul 9.4. Daca R si S sunt scheme de baze de
date si R conserva P, atunci ![]() este echivalenta cu
este echivalenta cu![]()
Demonstratia se obtine direct din echivalenta afirmatiilor 1) si 3) corolarul 1.
Teorema 9.6.
Daca R si S sunt scheme de
baze de date care conserva P,
atunci ![]() daca si
numai daca
daca si
numai daca ![]()
}tim deja ca atât conditia de unire cât si conditia de conservare a informatiei cer îndeplinirea proprietatii PR. De aceea, în cazul determinarii a adecvarii reprezentarii putem alege oricare din aceste conditii.
9.3 Verificarea adecvarii reprezentarii si a echivalentei determinata restrictii
Conditiile de unire si de independenta pe
componente sunt echivalente în cazul când, unirea transforma o baza de date din
L într-o relatie din Q. Diferentele între conditiile de
unire si conservare a informatiei constau în verificarea incluziunii P FIX(R) sau a unei conditii mai stricte ca ![]() . Daca P este SAT(C), pentru o multime oarecare de restrictii C,
aceste conditii se exprima ca
. Daca P este SAT(C), pentru o multime oarecare de restrictii C,
aceste conditii se exprima ca ![]()
![]()
![]() si pC
si pC![]()
![]() Amintim ca pC este notatia
neformala a proiectiei restrictiilor din C pe R, adica a restrictiilor care
determina multimea
Amintim ca pC este notatia
neformala a proiectiei restrictiilor din C pe R, adica a restrictiilor care
determina multimea ![]() . In acest fel pC se compune din acele restrictii
care satisfac p(r) ( pentru orice
. In acest fel pC se compune din acele restrictii
care satisfac p(r) ( pentru orice ![]() si R R
si R R
Am determinat pC anterior, astfel ca L =SAT(pC). Una din greutatile introducerii determinarii formale este aceea ca restrictiile din pC nu se exprima obligatoriu prin aceleasi tipuri de dependente ca si restrictiile din C. Deseori în pC se întâlnesc dependente de acelasi tip ca si în C, dar acolo pot apare dependente si de alt tip.
Exemplul 9.8. Fie U=ABCDE, R=ABCD, P=SAT(A E, B E, CE D).
Multimea F-dependentelor pe care trebuie sa le satisfaca proiectia p(r) pentru un r arbitrar din P este ![]() . Sa examinam relatia
s data in figura 1. Relatia s SAT(F), dar s nu este proiectia
nici unei instante din P. Daca
. Sa examinam relatia
s data in figura 1. Relatia s SAT(F), dar s nu este proiectia
nici unei instante din P. Daca ![]() sunt tupluri din p(r) astfel încât :
sunt tupluri din p(r) astfel încât :
1) ![]()
2) ![]()
3) ![]()
atunci :
4) ![]()
Aceasta dependenta nu este echivalenta cu nici o multime de F-dependente. Observam ca s nu satisface aceasta dependenta.
s (A B C D) s (A B C)
1 3 5
2 4 5 8 1 4 6
1 4 6 8 2 4 5
Figura 1 Figura 2
Exemplul 9.9. Fie U=ABCD, R=ABC, P=SAT
Proiectiile p(r) pentru un r arbitrar din P satisfac numai MV-dependentele triviale. Relatia s data în figura 2 nu este proiectia nici unei instante din P.
9.4. Cazul când P este definita numai de dependente functionale
S-a aratat mai sus ca în determinarea lui pC, si în verificarea incluziunii ![]() exista anumite greutati. In
cazul când C este compus doar din F-dependente este suficient sa se
examineze aceleasi dependente din pC
exista anumite greutati. In
cazul când C este compus doar din F-dependente este suficient sa se
examineze aceleasi dependente din pC
Teorema 9.7. Daca P=SAT(F) pentru o multime F de F-dependente atunci conditiile de componente independente, unire si conservare a informatiilor sunt echivalente.
Demonstratie. Din teorema 9.2 este suficient sa aratam ca,
daca AC1 sau AC2 nu sunt îndeplinite, nu vor fi îndeplinite nici IC1 si
nici IC2. Este evident ca neîndeplinirea lui AC1 duce la neîndeplinirea
lui IC1. Sa presupunem ca AC2 nu este îndeplinita, adica ![]() . Fie r o instanta din
. Fie r o instanta din ![]() . Se poate presupune ca r
este compus numai din doua tupluri. Deoarece relatia r nu satisface F exista o F-dependenta
X A care rezulta din F. Deoarece în r sunt numai doua tupluri, ele trebuie sa
coincida pe X si sa se deosebeasca în A, adica r are
valori ce coincid în coloanele X si doua valori în coloana A. Daca
IC2 nu este îndeplinita, atunci totul este demosntrat. Sa presupunem ca este îndeplinita.
Fie d=p(r). Baza de date d este în L. Din IC2 rezulta ca în P exista o instanta r,
astfel ca p(r')=d. Relatia r' în fiecare din
coloanele X poate avea doar o singura valoare. Dar r' trebuie sa aiba
doua valori în coloana A, din aceasta cauza r' contrazice
. Se poate presupune ca r
este compus numai din doua tupluri. Deoarece relatia r nu satisface F exista o F-dependenta
X A care rezulta din F. Deoarece în r sunt numai doua tupluri, ele trebuie sa
coincida pe X si sa se deosebeasca în A, adica r are
valori ce coincid în coloanele X si doua valori în coloana A. Daca
IC2 nu este îndeplinita, atunci totul este demosntrat. Sa presupunem ca este îndeplinita.
Fie d=p(r). Baza de date d este în L. Din IC2 rezulta ca în P exista o instanta r,
astfel ca p(r')=d. Relatia r' în fiecare din
coloanele X poate avea doar o singura valoare. Dar r' trebuie sa aiba
doua valori în coloana A, din aceasta cauza r' contrazice ![]() . In consecinta r P si IC2 nu este adevarata. Sa examinam
acum verificarea conditiilor de unire în cazul când P=SAT(F), unde F este o multime de F-dependente.
Vom verifica proprietatile LJ si J2. Proprietatea LJ se scrie ca
. In consecinta r P si IC2 nu este adevarata. Sa examinam
acum verificarea conditiilor de unire în cazul când P=SAT(F), unde F este o multime de F-dependente.
Vom verifica proprietatile LJ si J2. Proprietatea LJ se scrie ca
![]()
![]()
![]() . Ea se verifica cu ajutorul
algoritmului chase. Examinam numai verificarea lui J2 adica
. Ea se verifica cu ajutorul
algoritmului chase. Examinam numai verificarea lui J2 adica ![]() L P.
L P.
Definitia 9.16. Fie R schema bazei de date, F o multime
de F-dependente. Vom numi restrictie a lui F la R multimea
tuturor dependentelor din F+, care sunt aplicabile la o schema de
relatie R din R. Vom nota
aceasta multime ![]()
Exemplul 9.10. Fie U=ABCD, R=, F=.
F-dependentele netriviale din ![]() sunt:
sunt: ![]() , BC A, BC AB, BC AC, BC ABC, AB C.
, BC A, BC AB, BC AC, BC ABC, AB C.
Reamintim
ca F este constrânsa
(enforceable) la R daca![]() F.
F.
Lema 9.10. Fie P=SAT(F), unde F este o multime de F-dependente. Proprietatea J2 este îndeplinita daca si numai daca F FR
![]() Demontratie Necesitatea. Vom arata ca daca F FR, atunci în L
exista o baza de date d, astfel încât
Demontratie Necesitatea. Vom arata ca daca F FR, atunci în L
exista o baza de date d, astfel încât ![]() d P Fie
d P Fie ![]() si
si ![]() nu este în
nu este în ![]() . Fie Z închiderea lui X în
raport cu G. Este clar ca
. Fie Z închiderea lui X în
raport cu G. Este clar ca ![]() . Construim instanta
. Construim instanta ![]() din Q dupa cum urmeaza. Ea va fi
compusa din doua tupluri:
din Q dupa cum urmeaza. Ea va fi
compusa din doua tupluri: ![]() compus din 0 si
compus din 0 si ![]() cu 0 în partea Z si cu 1 în rest. Se vede
ca
cu 0 în partea Z si cu 1 în rest. Se vede
ca ![]() nu apartine lui P. Fie d=p(rX). Instanta
nu apartine lui P. Fie d=p(rX). Instanta ![]() nu este în P deoarece
nu este în P deoarece ![]() . Vom arata acum ca orice
relatie din d este proiectia unei instante din P. Fie R R. Definim instanta rR din P astfel încât pR(rX)=pR(rR).
. Vom arata acum ca orice
relatie din d este proiectia unei instante din P. Fie R R. Definim instanta rR din P astfel încât pR(rX)=pR(rR).
![]() contine doua tupluri:
contine doua tupluri: ![]()
![]() si tX compus doar din 1 în afara de locurile
din
si tX compus doar din 1 în afara de locurile
din ![]() pe F, în care se afla 0.
Instanta
pe F, în care se afla 0.
Instanta ![]() nu contrazice pe F, deoarece
nu contrazice pe F, deoarece ![]() ar fi incorect definita. Pentru a arata ca
pR(rX)=pR(rR)
trebuie aratat ca
ar fi incorect definita. Pentru a arata ca
pR(rX)=pR(rR)
trebuie aratat ca ![]() (aceste multimi sunt compuse din coloane
în care pR(rR) si pR(rX)
contin câte doua simboluri). Sa presupunem ca B este un
atribut continut doar de prima multime. Este clar ca
(aceste multimi sunt compuse din coloane
în care pR(rR) si pR(rX)
contin câte doua simboluri). Sa presupunem ca B este un
atribut continut doar de prima multime. Este clar ca ![]() . Deoarece
. Deoarece ![]() , atunci
, atunci ![]()
![]()
![]() . Dar atunci
. Dar atunci ![]()
![]()
![]() astfel ca
astfel ca ![]() si în consecinta B Z R. Am obtinut o contradictie deoarece
si în consecinta B Z R. Am obtinut o contradictie deoarece ![]() d P ceea ce înseamna ca J2
nu este îndeplinita.
d P ceea ce înseamna ca J2
nu este îndeplinita.
In continuare vom descrie un procedura de complexitate
polinomiala care permite sa verifice daca F este constrânsa la R.
Algoritmul 1 calculeaza ![]() în raport cu
în raport cu ![]() . Incluziunea
din pasul 2.1.1 se va face în raport cu F.
. Incluziunea
din pasul 2.1.1 se va face în raport cu F.
Procedure PCLOSURE (F,R,X;Y)
Y: X
Z=O
WHILE(Y Z) 3.0 Z=Y
3.1 FOR fiecare R R
Y:=((Y R)+ R) Y
3. return (Y)
Exemplul 9.11. Fie U=ABCDE, R=, F=.
Atunci PCLOSURE(F,R,A;ABC). Remarcam
ca ![]() pe F este ABCDE.
pe F este ABCDE.
Teorema 9.8. PCLOSURE(F,R,X;![]() ) calculeaza
) calculeaza ![]() în raport cu
în raport cu ![]() .
.
Demonstratie. Fie Y multimea returnata de
procedura. Atunci Y este o submultime a lui ![]() si ramâne
astfel pe parcursul aplicarii procedurii deoarece F-dependenta care
se foloseste în pasul 2.1.1 este în
si ramâne
astfel pe parcursul aplicarii procedurii deoarece F-dependenta care
se foloseste în pasul 2.1.1 este în ![]() (aceasta este (Y R) (Y R)+ R, unde
incluziunea se face în raport cu F). Vom arata
ca orice atribut din
(aceasta este (Y R) (Y R)+ R, unde
incluziunea se face în raport cu F). Vom arata
ca orice atribut din ![]() se va adauga la Y. Fie H un graf aciclic
orientat derivat din
se va adauga la Y. Fie H un graf aciclic
orientat derivat din ![]() al lui
al lui ![]() . Sa presupunem ca
. Sa presupunem ca ![]() sunt reperele vârfurilor grafului, numerotate
în ordinea în care apar în constructia lui
sunt reperele vârfurilor grafului, numerotate
în ordinea în care apar în constructia lui ![]() . Afirmam ca dupa
sfârsitul iteratiei i a ciclului while,
. Afirmam ca dupa
sfârsitul iteratiei i a ciclului while, ![]() . Se observa ca
. Se observa ca ![]() . Sa presupunem ca la
trecerea de la
. Sa presupunem ca la
trecerea de la ![]() la
la ![]() s-a folosit F-dependenta
s-a folosit F-dependenta ![]() . Deoarece
. Deoarece ![]() este în
este în ![]() , exista o schema de
relatie R R astfel ca
, exista o schema de
relatie R R astfel ca ![]() . Mai mult decât atât,
. Mai mult decât atât, ![]() astfel ca
astfel ca ![]() la începutul iteratiei (i+1). Când se
termina ciclul for ajungem la R, iar V apare ca submultime a lui
la începutul iteratiei (i+1). Când se
termina ciclul for ajungem la R, iar V apare ca submultime a lui ![]() atunci W (Y R)+ R deoarece
atunci W (Y R)+ R deoarece ![]()
![]()
![]() . Inseamna ca W se adauga la Y si
fiecare atribut
. Inseamna ca W se adauga la Y si
fiecare atribut ![]() care se adauga la
care se adauga la ![]() la trecerea spre
la trecerea spre ![]() se adauga respectiv la Y. Prin urmare, când
procedura se termina
se adauga respectiv la Y. Prin urmare, când
procedura se termina ![]() astfel ca
astfel ca ![]()
Lema 9.11. Ordinul de complexitate al procedurii PCLOSURE este O(|U|*|R|*||F||) unde ||F|| este numarul tuturor F-dependentelor din F.
Demonstratie: Ciclul while din pasul 2 nu se poate
realiza mai mult de ![]() ori deoarece Y nu poate deveni mai mare decît
U. Pentru fiecare iteratie a ciclului while, ciclul for din pasul 2.1 se
realizeaza de
ori deoarece Y nu poate deveni mai mare decît
U. Pentru fiecare iteratie a ciclului while, ciclul for din pasul 2.1 se
realizeaza de ![]() ori. Pasul 2.1.1 care calculeaza
ori. Pasul 2.1.1 care calculeaza ![]() se realizeaza într-un timp liniar dupa
se realizeaza într-un timp liniar dupa
![]() . In consecinta durata
totala a calculului are valoarea O(|U|*|R|*||F||).
. In consecinta durata
totala a calculului are valoarea O(|U|*|R|*||F||).
Teorema 9.8. Fie F este o multime de F-dependente si P=SAT(F).
Timpul de verificare a unei conditii de unire este polinomial în raport cu
![]() si
si ![]()
Demonstratie. Conform celor afirmate anterior, timpul de verificare al proprietatii LJ este polinomial.
Dupa lema 9.2 proprietatea J2 este adevarata daca ![]() . Pentru verificare este nevoie
doar de a arata ca
. Pentru verificare este nevoie
doar de a arata ca ![]()
![]()
![]() , ceea ce se poate face utilizând
algoritmul PCLOSURE pentru
fiecare dependenta
, ceea ce se poate face utilizând
algoritmul PCLOSURE pentru
fiecare dependenta ![]() din F prin testarea incluziunii Y
din F prin testarea incluziunii Y ![]() Acest test implica
Acest test implica ![]() apelari ale
procedurii PCLOSURE care are complexiate polinomiala.
apelari ale
procedurii PCLOSURE care are complexiate polinomiala.
Urmatoarele doua exemple demonstreaza ca proprietatile LJ si J2 sunt independente pe P, daca aceasta este descrisa de o multime dependente functionale.
Exemplul 9.12. Fie U=ABC, R=, P=SAT().
Proprietatea LJ este îndeplinita
pentru aceste date deoarece A C, dar
proprietatea J2 nu este îndeplinita deoarece ![]()
![]()
![]() nu are loc, prin
urmare F nu este constrânsa la R.
nu are loc, prin
urmare F nu este constrânsa la R.
Exemplul 9.13. Fie U si P aceleasi ca în
exemplul anterior si ![]() . Atunci F este
aplicabila la R si prin
urmare constrânsa la R, deci
proprietatea J2 este îndeplinita. Se observa ca LJ nu este adevarata
deoarece
. Atunci F este
aplicabila la R si prin
urmare constrânsa la R, deci
proprietatea J2 este îndeplinita. Se observa ca LJ nu este adevarata
deoarece ![]()
![]()
![]() nu are loc.
nu are loc.
9.5 Cazul când P este determinata de dependente functionale si multivoce
Anterior
s-a aratat cum se verifica conditia de unire daca P este definit de o multime de
dependente functionale. Acum se va da o procedura de verificare
a acestor conditii în cazul când ![]() unde C se compune din F-dependente si
din MV-dependente, iar R este
schema bazei de date în FN4. Este necesara verificarea proprietatilor
LJ si J2. Verificarea proprietatii LJ se reduce la definirea, cu
ajutorul algoritmului chase, a corectitudinii relatiei
unde C se compune din F-dependente si
din MV-dependente, iar R este
schema bazei de date în FN4. Este necesara verificarea proprietatilor
LJ si J2. Verificarea proprietatii LJ se reduce la definirea, cu
ajutorul algoritmului chase, a corectitudinii relatiei ![]()
![]()
![]() . Pentru verificarea proprietatii J2 este necesar sa
se verifice daca este adevarata încluziunea
. Pentru verificarea proprietatii J2 este necesar sa
se verifice daca este adevarata încluziunea ![]() L P ceea ce în limbajul dependentelor apare ca pC
L P ceea ce în limbajul dependentelor apare ca pC ![]()
![]() . S-a aratat deja ca verificarea implicatiei
din pC provoaca
greutati. Vom arata ca în cazul când R este o schema în FN4, este suficient sa se verifice ca
. S-a aratat deja ca verificarea implicatiei
din pC provoaca
greutati. Vom arata ca în cazul când R este o schema în FN4, este suficient sa se verifice ca
![]()
![]()
![]() , unde F este multimea
F-dependentelor care rezulta din C.
, unde F este multimea
F-dependentelor care rezulta din C.
Lema 9.12. Fie
R o schema de baza de date în FN4 si P=SAT(C), unde C este o multime de F- si MV-dependente. Fie F omultime
de F-dependente care rezulta
din C, iar ![]() o F-dependenta
din F care nu rezulta din
o F-dependenta
din F care nu rezulta din ![]() si
si ![]() . Atunci
. Atunci ![]() nu rezulta din
pC si
nu rezulta din
pC si ![]() (adica orice
instanta din
(adica orice
instanta din ![]() contrazice
contrazice ![]()
Demonstratie. Pe parcursul demonstratiei cu simbolul ![]() , unde V este o submultime a lui U, vom
nota o instanta compusa dintr-un tuplu format doar din 0 si
din a al doilea tuplu format din 0 pentru atributele din V si 1 în rest. Se
poate considera ca
, unde V este o submultime a lui U, vom
nota o instanta compusa dintr-un tuplu format doar din 0 si
din a al doilea tuplu format din 0 pentru atributele din V si 1 în rest. Se
poate considera ca ![]() în raport cu
în raport cu ![]() si
si ![]() deoarece
deoarece ![]() si
si ![]() nu atrage dupa sine
nu atrage dupa sine ![]() , deci va contrazice si
, deci va contrazice si ![]() . Fie rX
instanta determinata mai sus, iar d baza de date p(rX).
Deoarece
. Fie rX
instanta determinata mai sus, iar d baza de date p(rX).
Deoarece ![]() , iar rX
contrazice
, iar rX
contrazice ![]() , atunci si d contrazice
, atunci si d contrazice ![]() . Trebuie demonstrat ca
. Trebuie demonstrat ca ![]() d este în
d este în ![]() L. Vom arata ca d este
în L. Pentru aceasta vom arata ca
fiecare relatie din d este proiectia unei instante. Fie R o
schema de relatie din R,
Y=R X, iar
L. Vom arata ca d este
în L. Pentru aceasta vom arata ca
fiecare relatie din d este proiectia unei instante. Fie R o
schema de relatie din R,
Y=R X, iar ![]() ( 0-urile le consideram ca variabile
principale iar 1-urile ca secundare). Multimea coloanelor din
( 0-urile le consideram ca variabile
principale iar 1-urile ca secundare). Multimea coloanelor din ![]() , formate doar din 0 va coincide
cu Y+ în raport cu C. Dar Y+ R=R X deoarece pentru un atribut B Y+, F-dependenta Y B este în F, si în consecinta, este în
, formate doar din 0 va coincide
cu Y+ în raport cu C. Dar Y+ R=R X deoarece pentru un atribut B Y+, F-dependenta Y B este în F, si în consecinta, este în ![]() , astfel B X. Sa presupunem ca pR(rX) pR(r*). Atunci în r* trebuie sa
fie tuplu t ale carui 0-uri sunt pe locurile din W unde
, astfel B X. Sa presupunem ca pR(rX) pR(r*). Atunci în r* trebuie sa
fie tuplu t ale carui 0-uri sunt pe locurile din W unde ![]() . Din teorema chase-ului pentru
MV-dependente,
. Din teorema chase-ului pentru
MV-dependente, ![]()
![]() Y W,
astfel ca Y R W se realizeaza pe R. Dar relatia
Y W,
astfel ca Y R W se realizeaza pe R. Dar relatia ![]()
![]()
![]() nu este îndeplinita (deoarece
nu este îndeplinita (deoarece ![]() ). De aceea nu este îndeplinita
nici
). De aceea nu este îndeplinita
nici ![]()
![]()
![]() . Inseamna ca R nu este în FN4, ceea ce contrazice conditia. De aceea proiectiile
amintite mai sus trebuie sa coincida si în consecinta
d
. Inseamna ca R nu este în FN4, ceea ce contrazice conditia. De aceea proiectiile
amintite mai sus trebuie sa coincida si în consecinta
d ![]() L.
L.
Lema
9.13. Fie R o schema de baza de date în FN4, iar P=SAT(C), unde C este
o multime F-dependente si
MV-dependente. Sa
presupunem ca LJ este îndeplinita.
Fie F o multime de F-dependente care rezulta din C, iar MV-dependenta X―»Y rezulta
din C si nu rezulta din ![]() si
si ![]() . Atunci X Y nu rezulta din pC si
. Atunci X Y nu rezulta din pC si![]()
Demonstratie. Sa presupunem ca Y este o multime minimala
care satisface ipotezele, adica nici o submultime proprie Y' a multimii
Y nu satisface concomitent conditiile ![]()
![]() X-―»Y' si
X-―»Y' si ![]()
![]() X―»Y. Sa
presupunem ca X este multimea maxima satiface ipotezele. Atunci
X―»Y. Sa
presupunem ca X este multimea maxima satiface ipotezele. Atunci ![]() , în raport cu
, în raport cu ![]() si
si ![]() ca si în demonstratia lemei 9.12 si
nici o submultime proprie Z a multimii U-XY nu satisface concomitent
conditiile
ca si în demonstratia lemei 9.12 si
nici o submultime proprie Z a multimii U-XY nu satisface concomitent
conditiile ![]()
![]() XZ―»Y si
XZ―»Y si ![]()
![]() XY―»Y. Notam
cu
XY―»Y. Notam
cu ![]() aceeasi relatie ca în demonstratia
lemei 1. Este clar ca
aceeasi relatie ca în demonstratia
lemei 1. Este clar ca ![]() satisface
satisface ![]() . Afirmam ca
. Afirmam ca ![]() satisface de asemeni si
satisface de asemeni si ![]() . Presupunem ca nu este asa
atunci algoritmul chase aplicat la
. Presupunem ca nu este asa
atunci algoritmul chase aplicat la ![]() în raport cu
în raport cu ![]() si
si ![]() va adauga la
va adauga la ![]() noi tupluri. Fie t unul din tuplurile adaugate.
Vom nota cu XW multimea de atribute în care t este egal cu 0, caz în care
noi tupluri. Fie t unul din tuplurile adaugate.
Vom nota cu XW multimea de atribute în care t este egal cu 0, caz în care ![]() . Conform teoremei chase-ului
pentru MV-dependente,
. Conform teoremei chase-ului
pentru MV-dependente, ![]()
![]() X―»Y. Conform
proprietatii LJ avem
X―»Y. Conform
proprietatii LJ avem ![]()
![]()
![]() astfel ca
astfel ca ![]()
![]() X―»Y. Evident
ca
X―»Y. Evident
ca ![]() . Daca
. Daca ![]() , atunci
, atunci ![]()
![]() XZ―»Y unde
XZ―»Y unde ![]() . Multimea Z nu este vida
deoarece
. Multimea Z nu este vida
deoarece ![]() . Dependenta XZ―»Y nu rezulta din
. Dependenta XZ―»Y nu rezulta din ![]() si
si ![]() deoarece
XZ―»Y si X―»Y implica X―»Y (aceasta
este usor de verificat cu ajutorul algoritmului chase). De aceea
deoarece
XZ―»Y si X―»Y implica X―»Y (aceasta
este usor de verificat cu ajutorul algoritmului chase). De aceea ![]() contrazice maximalitatea lui X. Daca
contrazice maximalitatea lui X. Daca ![]() , atunci
, atunci ![]() contine Y si
contine Y si ![]()
![]() X―»W' ceea ce ce conduce la contrazicerea aceealesi
ipoteze. Singura posibilitate ramasa este ca Y sa se
intersecteze partial cu W. Fie
X―»W' ceea ce ce conduce la contrazicerea aceealesi
ipoteze. Singura posibilitate ramasa este ca Y sa se
intersecteze partial cu W. Fie ![]() , iar
, iar ![]() . Atunci
. Atunci ![]()
![]() . Dar din
. Dar din ![]() si
si ![]() nu poate sa rezulte concomitent X―»Y' si X―»Y" deoarece din ele rezulta prin aditivitate X―»Y ceea ce contrazice minimalitatea lui Y. De aceeea
aplicarea algoritmului chase la
nu poate sa rezulte concomitent X―»Y' si X―»Y" deoarece din ele rezulta prin aditivitate X―»Y ceea ce contrazice minimalitatea lui Y. De aceeea
aplicarea algoritmului chase la ![]() si
si ![]() nu adauga noi tupluri si înseamna
ca
nu adauga noi tupluri si înseamna
ca ![]() satisface
satisface ![]() în raport cu
în raport cu ![]() . A mai ramas de aratat
ca baza de date d=p(rX) este în L
ceea ce determina faptul ca
. A mai ramas de aratat
ca baza de date d=p(rX) este în L
ceea ce determina faptul ca ![]() d= rX sa fie în
d= rX sa fie în ![]() L. Deoarece
L. Deoarece ![]() în raport cu
în raport cu ![]() si
si ![]() din demonstratia lemei 1 rezulta ca
d L.
din demonstratia lemei 1 rezulta ca
d L.
Noi am obtinut un procedeu de verificare a conditiilor
de unire pentru scheme de baze de date
în FN4 si multimi de instante P, determinate de o multime
de F- si MV-dependente. Mai exact, la început, prin folosirea
algoritmului chase se verifica proprietatea LJ, adica ![]()
![]()
![]() . Apoi trebuie gasita o
multime de dependente functionale ce rezulta din C sau
o acoperire a sa. Din pacate pentru
aceasta nu se cunoaste nici o metoda cu exceptia verificarii.
Urmatorul pas consta în a-l determina pe
. Apoi trebuie gasita o
multime de dependente functionale ce rezulta din C sau
o acoperire a sa. Din pacate pentru
aceasta nu se cunoaste nici o metoda cu exceptia verificarii.
Urmatorul pas consta în a-l determina pe ![]() . Folosind algoritmul chase se poate
verifica îndeplinirea conditiei J2
pe calea verificarii
. Folosind algoritmul chase se poate
verifica îndeplinirea conditiei J2
pe calea verificarii ![]()
![]()
![]() . Acest proces nu este atât de
eficient ca în cazul când C este compus numai din F-dependente. Sa
remarcam ca în cazul în care C este compus din F-dependente si
J-dependente, iar schema R este
arbitrara, în general nu se cunoaste
nici o metoda de verificare a conditiei de unire.
. Acest proces nu este atât de
eficient ca în cazul când C este compus numai din F-dependente. Sa
remarcam ca în cazul în care C este compus din F-dependente si
J-dependente, iar schema R este
arbitrara, în general nu se cunoaste
nici o metoda de verificare a conditiei de unire.
Exemplul 9.14. Fie U=ABCD, R=,C=.
Multimea
de dependente ![]() acopera
acopera ![]() unde F este multimea deF-dependente care rezulta din C.
De aici
unde F este multimea deF-dependente care rezulta din C.
De aici ![]()
![]()
![]() . In afara de aceasta
. In afara de aceasta ![]() si
si ![]() determina pe C deoarece conditia de
unire este realizata în acest caz.
determina pe C deoarece conditia de
unire este realizata în acest caz.
Exemplul 9.15. Fie U=ABCDE, R=,C=.
Multimea
dependentelor ![]() acopera
acopera ![]() , dar
, dar ![]() împreuna cu
împreuna cu ![]() nu determina pe C deoarece conditia
de unire nu este îndeplinita.
nu determina pe C deoarece conditia
de unire nu este îndeplinita.
9.6 Verificarea echivalentei determinata de date
Pentru a verifica R PS unde P=SAT(C),
R si S scheme de baze de date, este necesar sa se determine daca
este îndeplinita egalitatea ![]() . Dupa cum s-a observat,
. Dupa cum s-a observat, ![]() se realizeaza când
se realizeaza când ![]() . Aceasta incluziune este
echivalenta cu conditia
. Aceasta incluziune este
echivalenta cu conditia ![]()
![]()
![]() care se poate verifica folosind algoritmul
chase în cazul când C este compusa din F-dependente si J-
dependente.
care se poate verifica folosind algoritmul
chase în cazul când C este compusa din F-dependente si J-
dependente.
Lema 9.14. Fie schemele de baze de date R si S si C o multime de F-si J-dependente. Sa presupunem ca ![]() . Atunci
. Atunci ![]() daca si numai daca
daca si numai daca ![]()
Observatie
: Lema 9.14 este utila deoarece ![]() este foarte usor de verificat. Ca sa
demonstram aceasta incluziune este necesar sa gasim
C-transformarea din
este foarte usor de verificat. Ca sa
demonstram aceasta incluziune este necesar sa gasim
C-transformarea din ![]() în
în ![]() . Deoarece în
. Deoarece în ![]() variabilele
principale nu se repeta, este necesar doar sa se verifice daca
pentru orice linie w din
variabilele
principale nu se repeta, este necesar doar sa se verifice daca
pentru orice linie w din ![]() exista o linie w'
din
exista o linie w'
din ![]() care include w.
care include w.
![]() (A B C D E)
(A B C D E) ![]() (A B C D E) T (A B C D E)
(A B C D E) T (A B C D E)
a1 a2 a3 b1 a5 a1 b1 a3 b2 a5 a1 a2 a3 b1 b2
b3 a2 a3 a4 a5 b3 a2 a3 a4 b4 b3 a2 b4 a4 b5
b5 b6 b7 a4 a5 a1 a2 a3 b6 a5
b3 b6 a3 a4 a5
b5 a2 b7 a4 a5
Figura 1 Figura 2 Figura 3
Exemplul 9.16. Fie U=ABCDE, S=, R=,
C= si P=SAT(C).
In figurile
1 si 2 sunt date ![]() . Avem C-transformarea din
. Avem C-transformarea din ![]() în
în ![]() astfel încât
astfel încât ![]() . Dar nu exista C-transformare din
. Dar nu exista C-transformare din ![]() în
în ![]() , astfel ca
, astfel ca ![]() .
.
Stim ca
![]() este echivalenta
cu
este echivalenta
cu ![]() când R si S
prezerva
când R si S
prezerva ![]() . Daca multumea C este compusa numai din F-dependente putem aplica la
. Daca multumea C este compusa numai din F-dependente putem aplica la ![]() si
si ![]() algoritmul chase. Fie
algoritmul chase. Fie ![]() si
si ![]() rezultatele aplicarii
algoritmului chase. Incluziunile
rezultatele aplicarii
algoritmului chase. Incluziunile ![]() se pot verifica deoarece C-transformarile
respective se pot determina usor în aceste cazuri.
se pot verifica deoarece C-transformarile
respective se pot determina usor în aceste cazuri.
Definitia 9.16. Fie T un tablou. Vom spune ca T
descrie F-dependenta ![]() daca exista o linie în
T care are variabile principale exact în
coloanele XY. Tabloul T descrie o multimea de F-dependente daca fiecare F-dependenta din aceasta multime
este descrisa de T.
daca exista o linie în
T care are variabile principale exact în
coloanele XY. Tabloul T descrie o multimea de F-dependente daca fiecare F-dependenta din aceasta multime
este descrisa de T.
Este evident ca,
multimea de F-dependente este constrânsa la schema bazei de date
R daca si numai daca![]() descrie orice acoperire G ale multimii F.
descrie orice acoperire G ale multimii F.
Exemplul 9.17. Tabloul T dat în figura 3 descrie multimea de F-dependente ![]()
Teorema 9.9. Fie R o schema de baza de date si F o multime neredundanta de F-dependente. Schema R conserva SAT(F), (FIX(R)=SAT(F)) daca si numai daca T*R=chaseF(TR) descrie F.
Pentru demonstatie vezi Maier/ /. Aceasta teorema sta la baza algoritmului de verificare a propietatii de conservare.
START
INPUT R, F
Call TR(R: TR) //procedura genereza![]() //
//
Call ChaseF(TR:T*,m)
d
FOR fiecare X Y din F
5.1 w
5.2 i
5.3 WHILE i m si w=0
5.3.1 IF ti(XY)=variabile principale
THEN
. 1 w
ELSE
. 2 i i+1
5.3.2 Continue
5.4 IF w=0
THEN
5.4.1 d 1
5.5 Continue
6. CASE d OF
6.2 OUTPUT
6.2 OUTPUT
7. STOP
|