VECTORI
directie
sens
|
|
B |
|
|
origine |
extremitate |
Operatii:- adunarea - cu regula paralelogramului:-se aduc vectorii în aceeasi origine
-se construieste un paralelogram care are doua
laturi exact cei doi vectori
-rezultanta este suma celor doi vectori
cu regula triunghiului : -se aseaza vectorii unul în continuarea celuilalt
-se uneste prima origine cu ultima extremitate
-vectorul obtinut este suma lor
- scaderea - se foloseste
faptul ca 
deci orice scadere devine o adunare
-înmultirea cu
scalar: 
este un vector cu
aceeasi directie , de 
ori mai mare ,cu
acelasi
sens
daca e pozitiv si cu sens opus daca e negativ.
Vectori
coliniari- paraleli:
si 
sunt coliniari daca
si numai daca exista un numar real astfel încât
.
sau 
unde 
si 
sunt versorii
(vectorii de pozitie ai axelor de
coordonate)
vectori
paraleli: 
vectori perpendiculari: 
produsul scalar :
unghiul a doi
vectori :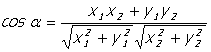 
daca A(
)si B(
) atunci vectorul 
|
