IV

Analiza starii de deformatie

Dupa cum s-a aratat, gradul de solicitare al unui corp se evidentiaza prin notiunea de tensiune. Tensiunea nu se poate masura direct. Tensiunile se pot determina cunoscānd marimea deformatiilor corpului.

Deoarece experimental masurarea deformatiilor se poate face numai pe suprafata exterioara a solidului, studiul starii plane de deformatie intereseaza īn mod deosebit. Īn ansamblul ei starea de deformatie reda modificarile geometrice ale corpului solicitat si indirect energia inmagazinata īn acesta.

Se numeste stare de deformatie īntr-u 19219v2119t n punct ansamblul marimilor ce permit caracterizarea distributiei deformatiilor īn jurul punctului.

IV.1 Deplasari si rotiri. Deformatii

Materialul

Otel carbon

Otel aliat

Fonta cenusie si alba

Bronz fosforos

Alama

Aliaje de aluminiu

Beton (marca 100-300)

Cauciuc

Pentru caracterizarea deformatiilor unghiulare se considera īn interiorul corpului un unghi drept, fig. (IV.5), cu laturile avānd lungimi elementare care, īn urma solicitarii, capata valoarea .

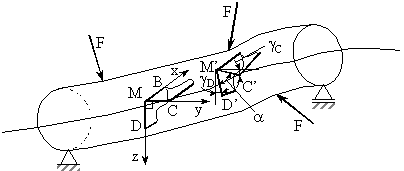
Fig. IV.5 Deformatii unghiulare

La limita diferenta dintre unghiuri are valoarea:

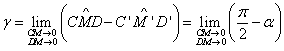, (IV.7)

unde (gama) reprezinta lunecarea specifica (s-a ales ca unitate de masura de referinta unghiul drept); se masoara īn radiani si este considerata pozitiva cānd unghiul drept se micsoreaza. Prin lunecarea specifica g, care are valori foarte mici exprimate īn radiani, se reflecta si deplasarea capetelor laturilor unghiului studiat īn baza ipotezei deformatiilor mici, fig. (IV.6).

Īn consecinta, īntr-o solicitare, unghiurile unui solid definit īn sistemul ortogonal Mxyz se vor modifica cu valorile , , . Primul indice reprezinta directia uneia din tensiunile t considerate, directie identica cu latura studiata din planul īn care se manifesta tensiunea, iar al doilea indice, defineste directia tangentei la traiectoria rotirii muchiei. Pentru cazul studiat, fig. (IV.5), se poate scrie:

Īn fig. (IV.6) este prezentata deformatia unghiulara a cubului elementar īntr-un singur plan yz.

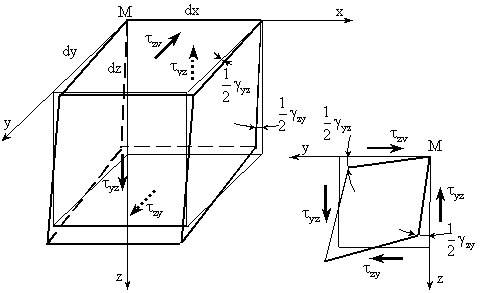
Fig. IV.6 Deformatia unghiulara a cubului elementar

IV.3 Tensorul deformatiilor. Deformatii principale;
directii principale

Ansamblul deformatiilor liniare si unghiulare definite de trei plane ortogonale cu originea īn M sunt suficiente pentru a determina starea de deformatie.

La fel ca si starea de tensiune, aceasta este determinata de sase componente distincte , , , , , . Avānd īn vedere relatiile (IV.10) si (IV.14) si tinānd seama de matricea deformatiilor din relatia (IV.7), rezulta tensorul deformatiilor specifice ce caracterizeaza complet starea de deformatie din jurul unui punct:

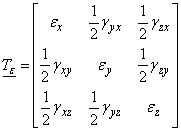(IV.15)

(IV.16)

. (IV.17)

(IV.18)

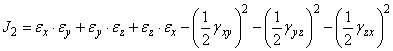(IV.19)

(IV.20)

unde este determinantul matricii asociate tensorului deformatiilor; scris pentru directiile principale 1, 2, 3 are forma:

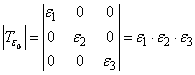(IV.21)

Pe directiile principale relatia (IV.16) se scrie:

(IV.22)

(IV.23)

La corpurile omogene si izotrope, directiile tensiunilor principale si ale deformatiilor principale coincid. Lunecarile maxime se dezvolta pe planele bisectoare ale planelor principale de deformatie si au valorile: g e e g e e g e e

Dimensiunile liniare ale paralelipipedului elementar dx, dy, dz variaza īn urma deformarii capatānd valorile , , . Variatia volumului elementar este:

(IV.24)

Neglijānd termenii infinit mici de ordin superior rezulta:

(IV.25)

Variatia specifica a volumului are valoarea:

(IV.26)

Se observa ca nu variaza cu modificarea sistemului de axe, fiind un invariant (J₁) al starii de deformatie.

Notānd cu intensitatea medie a deformatiilor specifice principale, adica

, (IV.27)

tensorul deformatiilor specifice scris pe directiile principale se poate descompune īn doi tensori de forma:

, (IV.28)

unde:

, (IV.29)

este numit tensor sferic al deformatiilor specifice, iar:

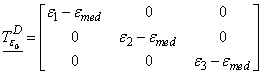(IV.30)

este numit tensor deviator al deformatiilor specifice.

Notānd , si , si facānd substitutie īn relatia (IV.26), variatia specifica a volumului este:

, (IV.31)

fapt ce conduce la concluzia ca tensorul deviator corespunde deformatiilor specifice ce reflecta numai modificarea formei corpului.

a fata de axa x. Dreptunghiul defineste o fata a paralelipipedului de grosime constanta studiat. Deplasarile si deformatiile punctului M si a vecinatatilor acestuia sunt reprezentate īn fig. (IV.10).

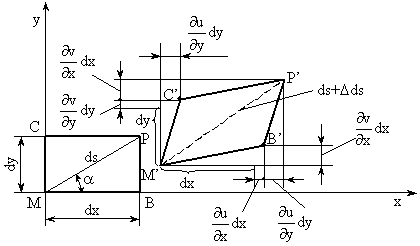
Fig. IV.10 Proiectia deplasarilor īn planul xy

Se observa ca marimea initiala a diagonalei are valoarea:

(IV.32)

Dupa deformare, diagonala capata valoarea:

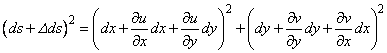(IV.33)

Dupa dezvoltarea parantezelor si neglijarea termenilor infinit mici de ordin superior si īmpartirea cu , rezulta lungirea specifica a diagonalei:

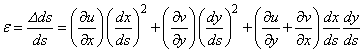(IV.34)

Avānd īn vedere relatiile dintre deplasari si deformatii, dupa īnlocuire expresia (IV.34) capata forma:

. (IV.35)

Relatia (IV.35) stabileste marimea deformatiei sub un unghi a fata de axa x (). Pentru argumentul 2a relatia capata forma:

(IV.36)

Relatia (IV.36) se poate obtine direct din expresia tensiunii facānd substitutia tensiunilor cu deformatiile corespondente. Continuānd analogia cu teoria tensiunilor, se poate afirma ca īn plan exista doua directii principale īn care lungirile au valori extreme si , iar lunecarile din planele ortogonale sunt nule.

(IV.37)

Prin acelasi rationament directiile lungirilor specifice principale se determina cu relatia:

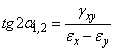(IV.38)

. (IV.39)

(IV.40)

(IV.41)

(IV.42)