
DEFINIRE. CLASIFICARE. CARACTERIZARE
Arborii sunt organe de masini cu miscare de rotatie destinate sa sustina alte organe de masini (roti dintate, roti de lant, roti de curea, semicuplaje etc.) în miscare de rotatie si sa transmita momente de torsiune în lungul axei lor.
Osiile sunt organe de masini cu miscare de rotatie sau fixe destinate numai sustinerii unor organe de masini în miscare de rotatie. Osiile nu transmit momente de torsiune.
|
Fig. 5.1 Partile componente ale unui arbore |
Tabelul 5.1
|
Forma axei geometrice |
Forma sectiunii transversale |
Forma suprafetei exterioare |
(cu mai mult de doua reazeme) |
||||
|
Forma sectiunii transversale |
(cu mai mult de doua reazeme) |
||||||
|
a
b Fig. 5.3 Osii |
MATERIALE sI TEHNOLOGIE
oteluri de uz general pentru constructii (OL 42, OL 50, OL 60 STAS 500/2), pentru arborii care nu necesita tratament termic;
oteluri carbon de caliate de îmbunatatire (OLC 45, OLC 60 STAS 880) sau oteluri aliate de îmbunatatire (40 Cr 10, 41 CrNi 12 etc. STAS 791), pentru arbori puternic solicitati si/sau durata mare de functionare impusa lagarelor sau canelurilor;
oteluri carbon de calitate de cementare (OLC 10, OLC 15 STAS 880) sau oteluri aliate de cementare (13 CrNi 30, 28 TiMnCr 12 etc. STAS 791), pentru arbori puternic solicitati si pentru arbori care functioneaza la turatii ridicate.
Semifabricatele pentru arbori si osii pot fi: bare laminate, pentru diametre sub 140 mm; bare laminate cu forjare ulterioara; bare laminate cu matritare ulterioara, în cazul productiei de de serie mare; semifabricate turnate, în cazul arborilor si osiilor de dimensiuni foarte mari. Executia arborilor din bare laminate cu forjare sau matritare ulterioara conduce la obtinerea unui semifabricat apropiat de forma finala a arborelui - cu importante economii de material, manopera si energie - si la realizarea unui fibraj continuu care urmareste forma arborelui, cu efect direct asupra maririi rezistentei acestuia.
Tehnologia de fabricatie a arborilor si osiilor consta în: strunjirea suprafetelor cilindrice sau conice si a filetelor, frezarea canalelor de pana sau a canelurilor - operatii executate înainte de tratamentul termic - rectificarea fusurilor, a portiunilor de calare, a suprafetelor canelurilor - operatii executate dupa tratamentul termic.
Tratamentele termice sau termochimice aplicate depind de materialul din care se executa arborii, putând fi: îmbunatatire sau îmbunatatire si calire superficiala a fusurilor, canelurilor, portiunilor de calare etc.; cementare urmata de calire a fusurilor, portiunilor de calare si a canelurilor; nitrurare etc.
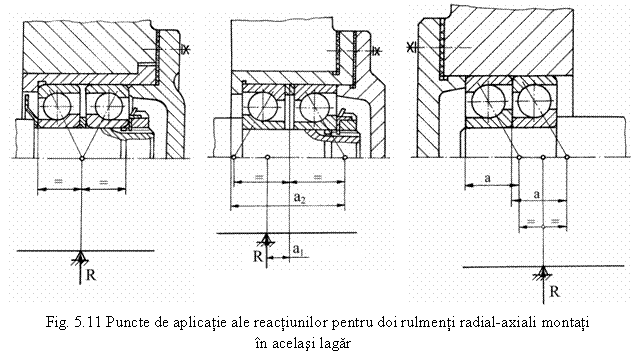
STABILIREA PUNCTELOR DE APLICAŢIE ALE FORŢELOR EXTERIOARE sI ALE REACŢIUNILOR DIN LAGĂRE
Stabilirea punctelor de aplicatie ale fortelor exterioare
Asupra unui arbore actioneaza forte - provenite de la rotile de transmisie montate pe acesta (roti dintate, roti de curea, roti de lant etc.) sau de la manivelele unor mecanisme - numite forte exterioare. Aceste forte actioneaza în plane normale pe axa arborelui sau în plane axiale fiind paralele cu axa arborelui. Fortele normale sunt fortele tangentiale si radiale din angrenaje, fortele din transmisiile prin curele sau lant, fortele din manivelele mecanismelor etc. si se transmit arborelui prin contactul dintre butuc si arbore. Fortele axiale provin în general din angrenaje (fortele axiale care apar la angrenajele cilindrice cu dantura înclinata, conice, melcate etc.) si se transmit arborelui prin intermediul umerilor sau a unor inele de sprijin.
Fortele exterioare actioneaza asupra arborilor într-un singur plan - fortele din transmisiile prin curea sau prin lant - sau în doua plane perpendiculare - fortele din angrenaje (fortele tangentiale actioneaza într-un plan, iar fortele radiale si cele axiale în celalalt plan).
Relatiile de determinare a marimilor fortelor exterioare sunt prezentate la capitolele respective (angrenaje, transmisii prin curele, transmisii prin lant etc.) [5, 11]. Pe lânga marimea fortelor exterioare, pentru întocmirea schemei de calcul al arborelui, intereseaza si punctul de aplicatie al acestor forte.
|
Fig. 5.5 Forte exterioare provenite de la roti de curea sau lant |
|
Fig. 5.6 Forte exterioare provenite de la Fig. 5.7 Forte exterioare provenite de la roti dintate cilindrice roti dintate conice |
Se întocmeste schema de
calcul considerând ca punctul de aplicatie al reactiunii ![]() este la mijlocul distantei dintre
rulmenti (punctul B' din fig. 5.14, a).
este la mijlocul distantei dintre
rulmenti (punctul B' din fig. 5.14, a).
Se întocmeste schema de calcul prin încarcarea arborelui cu fortele exterioare în cele doua plane, orizontal (H) si vertical (V).


 Se
determina marimile reactiunilor
Se
determina marimile reactiunilor ![]() , respectiv
, respectiv ![]() din cele doua
plane caracteristice si apoi reactiunea din punctul B',
din cele doua
plane caracteristice si apoi reactiunea din punctul B', ![]() .
.
Se
determina forta axiala suplimentara ![]() , Y fiind factorul axial care se ia din
catalogul de rulmenti.
, Y fiind factorul axial care se ia din
catalogul de rulmenti.
În
functie de tipul rulmentilor radial-axiali, cu bile sau cu role
conice, si de raportul ![]() , din fig. 5.13
[110] se determina raportul
, din fig. 5.13
[110] se determina raportul ![]() si cunoscând distanta a2,
se calculeaza distanta a1.
si cunoscând distanta a2,
se calculeaza distanta a1.
Se
determina distanta ![]() stabilindu-se pozitia punctului de
aplicatie al reactiunii RB. Cu distanta dintre
reactiuni l se recalculeaza reactiunile RA
si RB.
stabilindu-se pozitia punctului de
aplicatie al reactiunii RB. Cu distanta dintre
reactiuni l se recalculeaza reactiunile RA
si RB.
CALCULUL ARBORILOR
Solicitarile arborilor si ciclurile de variatie ale acestora
Sub actiunea fortelor exterioare si a momentelor de torsiune pe care le transmit, arborii sunt solicitati la torsiune, încovoiere si tractiune sau compresiune. Aceste solicitari actioneaza simultan, deci arborii sunt supusi la solicitari compuse. Ca urmare a acestor solicitari, în interiorul arborelui apar tensiuni interne - normale sau tangentiale - si tensiuni de suprafata - de strivire - între arbore si organele de masini sustinute.
Principalele solicitari sunt solicitarea de torsiune si cea de încovoiere. Aceste solicitari pot duce la ruperea statica a arborilor, iar variatia acestora dupa cicluri de solicitare diferite pot duce la ruperea arborelui prin oboseala materialului, în zonele cu concentratori de tensiune.
|
Fig. 5.15 Variatia tensiunilor de încovoiere datorita rotatiei arborelui |
Cele mai uzuale situatii de functionare a arborilor sunt când directia sarcinii este constanta, caz în care, la o rotatie completa a arborelui, fiecare fibra a materialului trece odata prin dreptul directiei sarcinii. În acest mod functioneaza arborii reductoarelor de turatie, cutiilor de viteze, de distributie si transmisiile centrale ale autovehiculelor, transmisiilor masinilor unelte etc. Ca urmare a acestui mod de functionare, tensiunea de încovoiere variaza dupa un ciclu alternant simetric (fig. 5.15). Fibrele arborelui sunt supuse alternativ la compresiune (fibra A) sau la tractiune (fibra B), iar dupa o rotire a arborelui cu 180ș, la compresiune (fibra B) si la tractiune (fibra A).
Tensiunile de torsiune pot fi constante (exemplu: arborii transmisiilor de actionare a ventilatoarelor si pompelor de debit si presiune constante, cu rare întreruperi în functionare) sau variabile, dupa un ciclu pulsator (exemplu: arborii transmisiilor care functioneaza cu încarcari si descarcari frecvente sau cu opriri dese) sau alternant simetric (exemplu: arborii amplasati dupa cutia de viteze din transmisiile tractoarelor industriale sau de îmbunatatiri funciare, tractoare care functioneaza cu schimburi frecvente ale sensului de deplasare, înainte si înapoi).
Schitele ciclurilor de variatie a tensiunilor de încovoiere si de torsiune si caracteristicile acestor cicluri sunt prezentate în tabelul 5.2.
Tabelul 5.2
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculul de rezistenta al arborilor
Pentru a prelua tensiunile de interior (de torsiune si de încovoiere) diversele diametre ale arborelui se determina din conditii de rezistenta sau din conditii constructive. Pentru a rezista la solicitari variabile (oboseala), datorita variatiei tensiunilor de încovoiere si/sau de torsiune, sectiunile cu concentratori de tensiuni se verifica prin calcule la solicitari variabile.
În continuare, se prezinta etapele si recomandarile pentru calculul arborilor.
Calculul de predimensionare
Predimensionarea are drept scop determinarea preliminara a diametrului arborelui, necesar la întocmirea schemei subansamblului arbore - organe de masini sustinute si de rezemare si la întocmirea schemei de calcul la solicitari compuse. Predimensionarea se face din conditia de rezistenta la solicitarea de torsiune, utilizând o rezistenta admisibila conventionala, care prin valorile reduse acceptate evidentiaza faptul ca arborele este solicitat si la încovoiere.
În cazul arborilor plini, diametrul se determina cu relatia
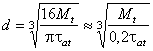 (5.1)
(5.1)
 (5.2)
(5.2)
alegându-se, initial, raportul dintre
diametrul interior d1 si cel exterior d al arborelui
din intervalul ![]() [16]. Diametrele obtinute se rotunjesc la
valori întregi.
[16]. Diametrele obtinute se rotunjesc la
valori întregi.
Tensiunea
admisibila conventionala se alege din intervalul ![]() MPa, valorile mai mari se recomanda în
cazul arborilor scurti, iar valorile mai mici în cazul arborilor lungi. În
cazul unor arbori foarte rigizi si la care deformatiile de încovoiere
nu conduc la functionari incorecte ale ansamblului respectiv (de
exemplu, arborele de iesire din reductoarele cu doua sau trei
trepte), se pot lua si valori mai mari pentru rezistenta
admisibila conventionala la torsiune,
MPa, valorile mai mari se recomanda în
cazul arborilor scurti, iar valorile mai mici în cazul arborilor lungi. În
cazul unor arbori foarte rigizi si la care deformatiile de încovoiere
nu conduc la functionari incorecte ale ansamblului respectiv (de
exemplu, arborele de iesire din reductoarele cu doua sau trei
trepte), se pot lua si valori mai mari pentru rezistenta
admisibila conventionala la torsiune, ![]() MPa. Pentru arborii reductoarelor cu doua
trepte, se recomanda urmatoarele valori pentru rezistentele
admisibile conventionale la torsiune:
MPa. Pentru arborii reductoarelor cu doua
trepte, se recomanda urmatoarele valori pentru rezistentele
admisibile conventionale la torsiune: ![]() MPa, pentru arborele de intrare;
MPa, pentru arborele de intrare; ![]() MPa, pentru arborele intermediar;
MPa, pentru arborele intermediar; ![]() MPa, pentru arborele de iesire.
MPa, pentru arborele de iesire.
Calculul la solicitari compuse
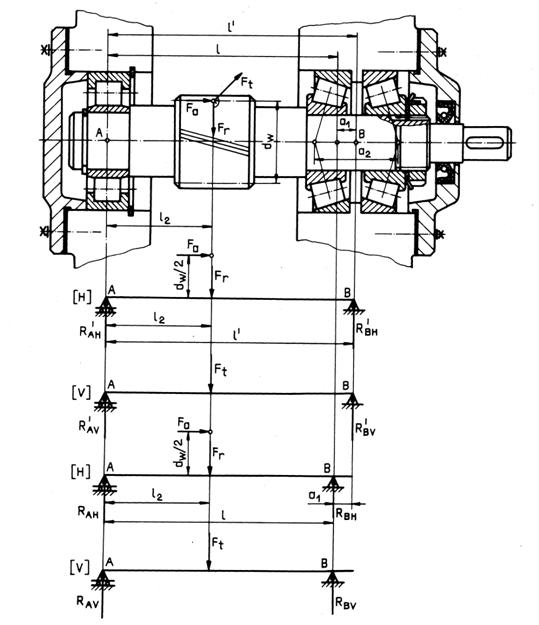
Pentru calculul la solicitari compuse, arborele trebuie reprezentat sub forma unei grinzi, pe doua reazeme, încarcata cu fortele exterioare provenite de la organele de masini sustinute de acesta. Pentru a întocmi aceasta schema de calcul, este necesar sa se realizeze schita subansamblului arbore - organe de masini sustinute - lagare cu rulmenti, schita care se întocmeste numai dupa ce s-a efectuat calculul angrenajelor, s-au ales preliminar rulmentii si sistemul de etansare. La întocmirea schitei subansamblului (spre exemplificare, în fig. 5.16 se prezinta arborii de intrare si intermediar ai unui reductor cilindric orizontal cu doua trepte) se tine seama de urmatoarele:
|
Fig. 5.16 Schita subansamblului arborilor de intrare si intermediar ai unui reductor cilindric cu doua trepte |
diametrul obtinut la predimensionare este diametrul portiunii de calare a rotii, pentru arborele intermediar si cel de iesire, si diametrul de lânga pinion pentru arborele de intrare
la stabilirea diametrelor treptelor arborelui se tine seama de marimea umerilor de sprijin pentru organele de masini sustinute (roti dintate, roti de curea, roti de lant, semicuplaje etc.), de diametrul impus de sistemul de etansare (ales din standardul etansarii respective), de diametrele interioare ale rulmentilor (alese din catalogul de rulmenti);
lungimile diferitelor portiuni ale arborelui se stabilesc tinând seama de latimile rotilor dintate (stabilite din calculul de rezistenta al angrenajelor celor doua trepte), latimile sistemului de etansare si ale rulmentilor, precum si distantele dintre roti sau dintre roti si marginile carcasei etc.
Pe baza schemei din fig. 5.16, rezulta distantele dintre punctele de aplicatie ale fortelor exterioare si dintre acestea si punctele de aplicatie ale reactiunilor din lagare, pentru arborele intermediar:
![]()
![]() ; (5.3)
; (5.3)
![]() ,
,
respectiv indice V, pentru planul vertical), diagramele de momente încovoietoare în cele doua plane). Fortele axiale din lagare produc momente încovoietoare concentrate, determinate cu relatiile
![]() . (5.4)
. (5.4)
Fig. 5.17 Schema de calcul la solicitari compuse pentru arborele intermediar al unui reductor cu doua trepte, cilindric obisnuit
Ecuatia de momente în punctul D, pentru planul orizontal, este
![]() , (5.5)
, (5.5)
![]() , (5.6)
, (5.6)
![]() , (5.7)
, (5.7)
![]() . (5.8)
. (5.8)
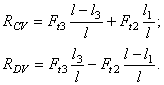 (5.9)
(5.9)
![]()
![]() . (5.10)
. (5.10)
![]() . (5.11)
. (5.11)
În continuare, se traseaza diagrama fortelor axiale si diagrama de momente încovoietoare - în planul orizontal - diagrama de momente de torsiune si diagrama de momente încovoietoare - în planul vertical (v. fig. 5.17) si se stabilesc sectiunile periculoase ( sectiunile 2 si 3 ale arborelui intermediar reprezentat în fig. 5.17).
Solicitarile din cele doua sectiuni periculoase 2 si 3 sunt:
compresiune data de forta Fa3, tensiunile produse fiind
![]() ; (5.12)
; (5.12)
torsiune data de momentul de torsiune Mt
![]() ; (5.13)
; (5.13)
încovoiere data de momentele încovoietoare maxime, obtinute prin însumarea geometrica a momentelor încovoietoare maxime din cele doua plane, orizontal si vertical; rezultând
![]() (5.14)
(5.14)
pentru sectiunea 2, respectiv
![]() (5.15)
(5.15)
Actionând simultan cele doua tensiuni, normale si tangentiale, calculul la solicitari compuse consta în determinarea unei tensiuni echivalente
![]() (5.16)
(5.16)
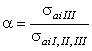 (5.17)
(5.17)
în care ![]() reprezinta rezistenta
admisibila la încovoiere a materialului arborelui dupa ciclul
constant (I), pulsator (II) sau alternant simetric (III).
Valori orientative pentru rezistentele admisibile la încovoiere, pentru
arbori din otel, pentru cele trei cicluri de solicitare, se dau în
lucrarile [6, 14, 23].
reprezinta rezistenta
admisibila la încovoiere a materialului arborelui dupa ciclul
constant (I), pulsator (II) sau alternant simetric (III).
Valori orientative pentru rezistentele admisibile la încovoiere, pentru
arbori din otel, pentru cele trei cicluri de solicitare, se dau în
lucrarile [6, 14, 23].
Cu tensiunile stabilite, se poate verifica arborele la solicitari compue sau se poate redimensiona arborele.
Pentru verificarea arborelui la solicitari compuse, în sectiunile periculoase, trebuie sa se îndeplineasca conditia
![]() (5.18)
(5.18)
Daca nu se îndeplineste aceasta conditie sau daca diferenta dintre aceste tensiuni este prea mare, se recomanda dimensionarea arborelui la solicitari compuse.
Pentru dimensionarea arborelui la
solicitari compuse, se impune conditia ![]() si tinând seama ca
si tinând seama ca ![]() si considerând σtc = 0, se obtine modulul de
rezistenta necesar la încovoiere
si considerând σtc = 0, se obtine modulul de
rezistenta necesar la încovoiere
![]() , (5.19)
, (5.19)
respectiv diametrul necesar al arborelui
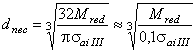 .
.
Verificarea la solicitari variabile
Scopul calculului la solicitari variabile este de a evita ruperea arborilor prin oboseala materialului si consta în determinarea unui coeficient de siguranta - în sectiunile în care exista concentratori de tensiuni (salturi de diametre, degajari, canale de pana, caneluri, filete, ajustaje presate etc.) - si compararea acestuia cu un coeficient de siguranta considerat admisibil, determinat experimental.
Coeficientii de siguranta la oboseala se calculeaza în functie de solicitarile arborilor din sectiunea cu concentrator de tensiune dupa una din metodele date de Rezistenta materialelor (metoda Serensen, metoda Soderberg, metoda Buzdugan etc.). Cea mai utilizata este metoda Serensen, pe baza careia sunt prezentate relatiile pentru calculul coeficientilor de siguranta la oboseala:
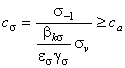 (5.21)
(5.21)
 unde
unde ![]() (5.22)
(5.22)
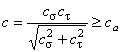 (5.23)
(5.23)
Tensiunile σ-1, σ 0, τ -1 si τ 0 reprezinta tensiunile de rupere prin oboseala pentru solicitarea de încovoiere (σ) sau pentru cea de torsiune (τ) corespunzatoare ciclului de solicitare alternant simetric (-1) sau pulsator (0), determinate în functie de materialul arborelui [7, 23].
Tensiunile v m v si m (v. tabelul 5.2) sunt determinate de marimea solicitarii efective si de caracteristica ciclului de variatie a acesteia.
Coeficientii k si , respectiv k si [7, 16, 23], sunt coeficienti de corectie care tin seama de faptul ca tensiunile de oboseala, determinate pe epruvete standard, trebuie corectate în functie de formele concrete ale arborelui - tipuri de concentratori, dimensiuni, calitate a suprafetei si tratament termic diferite fata de cele ale epruvetei. Coeficientii de concentrare a tensiunii k si k se aleg în functie de tipul si dimensiunile concentratorului de tensiuni (canal de pana, trecere de sectiune, filet etc) si de materialul arborelui. Coeficientii dimensionali si tin seama de diametrul arborelui si de materialul acesuia. Coeficientii de calitate a suprafetei si depind de modul de prelucrare a suprafetei si de tratamentul termic aplicat.
Rezistenta la oboseala a arborilor este data de marimea coeficientului de siguranta determinat cu una din relatiile (5.21), (5.22) sau (5.23). Umarind aceste relatii se poate observa ca marirea rezistentei la oboseala poate fi realizata prin: alegerea unui material cu caracteristici mecanice mai bune (prin cresterea tensiunilor ) sau prin micsorarea concentratorilor de tensiuni (modificarea coeficientilor k si , respectiv k si
Cel mai întâlnit procedeu utilizat pentru marirea rezistentei la oboseala este micsorarea concentratorului de tensiuni prin masuri constructive.
În cazul trecerilor de diametre care nu sunt utilizate ca umeri de sprijin pentru organele de masini montate pe arbore, se recomanda [14, 23, 32, 33] urmatoarele solutii (fig.5.18):
raza de racordare cât mai mare (fig. 5.18, a), doua raze de racordare diferite (fig. 5.18, b), racordare de forma eliptica (fig. 5.18, c) în cazul arborilor foarte solicitati;
tesirea capatului de diametru mai mare (fig. 5.18, d), tesire urmata de racordare (fig. 5.18, e) la salturi mari de diametre;
raza de racordare combinata cu canal de descarcare (fig. 5.18, f);
gaura interioara în portiunea de arbore cu diametru mai mare (fig. 5.18, g).
Fig. 5.18 Masuri constructive pentru reducerea concentratorului de tensiuni la trecere de diametru fara rezemare
Daca trecerea de diametru este utilizata pentru rezemarea axiala a unor organe de masini sau daca treapta de diametru mai mic trebuie rectificata, se recomanda una din urmatoarele solutii:
cu canal de trecere executat la capatul treptei cu diametru mai mic (fig. 5.19, a), dimensiunile acestuia fiind b = 2,5.3 mm si t = 0,25.0,5 mm, pentru d ≤ 50 mm, respectiv, b = 4.5 mm si t = 0,5.1 mm, pentru d > 50 mm, marirea latimii b (fig. 5.19, b) reducând concentratorul de tensiuni;
cu degajare interioara în umarul de sprijin (fig. 5.19, c), mai greu de executat dar fara sa reduca diametrul treptei mici;
cu canal de trecere combinat cu degajare interioara (fig. 5.19, d);
cu raza de racordare cat mai mare (fig. 5.19, e si f), caz în care alezajul piesei sprijinita axial necesita o tesire sau o raza de racordare marita, uneori utilizându-se piese intermediare (fig. 5.19, f).
canalele de pana sa fie executate cu freza deget - cu capetele rotunjite (fig. 5.20, a), deoarece reprezinta un concentrator de tensiuni mai redus decât canalele de pana executate cu freza disc rotunjite (fig. 5.20, b);
diametrul exterior al portiunii canelate sa fie egal cu diametrul arborelui (fig. 5.20, c), iar trecerea de la partea canelata la cea necanelata sa se faca prin raze mari de racordare.
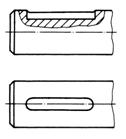

Fig. 5.20 Forme constructive pentru canale de pana sau caneluri practicate în arbore
La marginile portiunilor de sprijin al organelor de masini, pe arbori apar concentrari de tensiuni care pot fi diminuate prin urmatoarele masuri constructive:
marirea diametrului portiunii de sprijin (fig. 5.21, a);
rotunjirea sau tesirea alezajului din butuc (fig. 5.21, b);
executarea unor canale de degajare în arbore (fig. 5.21, c);
marirea elasticitatii butucului prin formele constructive prezentate în fig. 5.21, d sau e;
combinarea unor solutii prezentate anterior (fig. 5.21, f).
Verificarea arborelui la deformatii
Sub actiunea sarcinilor exterioare, arborii sufera deformatii de încovoiere si de torsiune. Calculul arborelui la deformatii este un calcul de verificare, efectuat în scopul preîntâmpinarii functionarii necorespunzatoare a organelor de masini sustinute si a lagarelor.
Verificarea arborelui la deformatii de încovoiere consta în stabilirea deformatiilor efective (sageti în dreptul fortelor exterioare si unghiuri de rotire în lagare) si compararea acestora cu deformatiile maxime admise.
Deformatiile se determina prin una din metodele cunoscute din Rezistenta materialelor, metode bazate pe ecuatia fibrei medii deformate (integrarea analitica a ecuatiei diferentiale a fibrei medii deformate, metoda grinzilor fictive, metoda ecuatiei celor doua rotiri si a celor doua sageti, metoda ecuatiei celor trei sageti) sau pe expresiile energiei de deformatie, bazate pe ecuatia Mohr-Maxwell, teorema lui Castiliano, teorema lui Betti; metoda Mohr-Maxwell-Veresceaghin etc.
În cazul în care fortele exterioare actioneaza în doua plane perpendiculare, se determina separat deformatiile din cele doua plane, orizontal (δH, φH ) si vertical (δV, φV ), deformatiile totale obtinându-se prin însumarea geometrica a deformatiilor din cele doua plane.
![]() ;
; 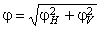 . (5.24)
. (5.24)
Deformatiile efective de încovoiere ale arborilor trebuie sa fie mai mici decât deformatiile admisibile (δ ≤ δa; φ ≤ φa), care depind de conditiile de functionare ale ansamblului din care face parte arborele. Pentru evitarea modificarii exagerate a jocurilor din angrenaje, sagetile în dreptul rotilor dintate se limiteaza la valori admisibile δa = (0,01.0,03)m, unde m este modulul danturii. Pentru functionarea corespunzatoare a lagarelor, unghiurile de rotire din lagare se limiteaza la valorile admisibile dependente de tipul lagarului (lagar cu alunecare, lagar cu rulmenti radiali cu bile sau role cilindrice, lagar cu rulmenti oscilanti etc.).
|