Nr. etapei	Data	Etapa	Procent	Semnatura cadrului didactic
		Primirea temei de proiect.
		Al 646i88g egerea motorului electric. Calculul energetic al transmisiei mecanice. Calculul puterilor, turatiilor si momentelor de torsiune pe fiecare arbore. Al 646i88g egerea si verificarea cuplajelor. Predimensionarea arborilor de transmisie. Calculul transmisiei cu curele.
		Calculul integral al lagarului radial hidrodinamic. Desen de ansamblu preliminar al lagarului hidrodinamic.
		Predimensionarea angrenajului. Calculul elementelor geometrice caracteristice ale angrenajului. Desen de ansamblu definitiv al lagarului hidrodinamic.
		Verificarea angrenajului din punct de vedere al rezistentei mecanice. Al 646i88g egerea penelor. Desen de ansamblu preliminar al reductorului.
		Proiectarea constructiva a arborilor transmisiei. Verificarea arborilor la oboseala. Al 646i88g egerea si verificarea rulmentilor. Desen de ansamblu avansat al reductorului.
		Calculul de incalzire al reductorului. Desen de ansamblu definitiv al reductorului. Desen de executie preliminar al arborelui.
		Desen de executie definitiv. Transcrierea proiectului.
		Predare si sustinere proiectului.

UNIVERSITATEA POLITEHNICA BUCURESTI STUDENT: Huiban V. Valeriu Cristian

FACULTATEA DE INGINERIE MECANICA AN: III GRUPA: 932

CATEDRA: O.M.T. INDR. PR.: s. l. dr. ing. LUCIAN SEICIU

TEMA DE PROIECT

Sa se proiecteze o transmisie mecanica alcatuita din:

ME – motor electric asincron trifazat

TCT – transmisie prin curele trapezoidale

R – reductor de turatie cu roti dintate cilindrice cu dinti inclinati

CEB – cuplaj elastic cu bolturi

CRF – cuplaj rigid cu flansa

LHD – lagar hidrodinamic

ML – masina de lucru

Arborele rotii mari de curea este sprijinit pe doua lagare hidrodinamice radiale independente, cu racire naturala si ungere prin inel.

Se dau:

puterea la arborele masinii de lucru: P_ML = 17 kW

turatia arborelui masinii de lucru: n_ML = 180 rotmin

coeficientul de suprasarcina: b = 1,6. Schema cinematica a transmisiei mecanice propuse se prezinta in figura de mai jos:

CUPRINS

1.1. Al 646i88g egerea motorului electric …………………………………………………………..

1.2. Calculul cinematic ……………………………………………………………………

1.3. Calculul energetic …………………………………………………………………….

Predimensionarea arborilor ………………………………………………………………..

Proiectarea transmisiei prin curele trapezoidale …………………………………………..

3.1. Al 646i88g egerea tipului curelei ……………………………………………………………….

3.2. Al 646i88g egerea diametrului primitiv al rotii mici ……………………………………………

3.3. Calcularea diametrului primitiv al rotii mari ………………………………………….

3.4. Distanta preliminara intre axe …………………………………………………………

3.5. Unghiul dintre ramurile curelei ………………………………………………………..

3.6. Unghiul de infasurare ………………………………………………………………….

3.7. Lungimea primitiva a curelei …………………………………………………………..

3.8. Viteza periferica a curelei ……………………………………………………………

3.9. Numarul de curele (preliminar) ………………………………………………………..

3.10. Frecventa indoirii curelelor …………………………………………………………….

3.11. Forta periferica transmisa ………………………………………………………………

Calculul lagarului hidrodinamic …………………………………………………………….

4.1. Stabilirea temperaturilor de echilibru termic …………………………………………

4.2. Calculul parametrilor pentru temperaturile de echilibru ……………………………….

4.3. Al 646i88g egerea ajustajului si a raportului B/D optim …………………………………………

Calculul angrenajului ………………………………………………………………………..

5.1. Predimensionarea angrenajului …………………………………………………………

Al 646i88g egerea materialelor pentru rotile dintate si a tratamentelor termice sau termochimice ……………………………………………………………………

Predimensionarea angrenajului ………………………………………………….

5.2. Calculul elementelor geometrice ale rotilor dintate …………………………………….

5.3. Calculul fortelor din angrenaj …………………………………………………………..

5.4. Verificarile angrenajului ………………………………………………………………..

Verificarea incadrarii in limitele angrenarii si generarii ………………………

Verificarea rezistentei danturii rotilor dintate …………………………………

Verificarea dimensionala a danturii rotilor dintate ………………………………

Calculul reactiunilor. Diagrama de momente incovoietoare si de torsiune ………………….

6.1. Arborele pinion ………………………………………………………………………….

6.2. Arborele rotii conduse …………………………………………………………………..

Al 646i88g egerea si verificarea rulmentilor …………………………………………………………..

Al 646i88g egerea si verificarea penelor ………………………………………………………………

Al 646i88g egerea si verificarea cuplajelor …………………………………………………………….

9.1. Cuplajul elastic cu bolturi ………………………………………………………………..

9.2. Cuplajul cu flanse ………………………………………………………………………..

Verificarea arborilor ………………………………………………………………………….

10.1. Verificarea la oboseala …………………………………………………………………..

10.2. Verificarea la solicitare compusa ………………………………………………………..

10.3. Verificarea deformatiilor arborilor ………………………………………………………

10.4. Verificarea la vibratii …………………………………………………………………….

Al 646i88g egerea lubrifiantului si a sistemului de ungere al angrenajului ……………………………

Calculul termic al reductorului cu roti dintate …………………………………………………

12.1. Calculul randamentului total al reductorului ……………………………………………

12.2. Calculul temperaturii de functionare a reductorului ………………………………………

A. MEMORIU TEHNIC

Al 646i88g egerea motorului electric. Calculul cinematic si energetic

Al 646i88g egerea motorului electric

Intrucat datele initiale prevad cunoasterea puterii la arborele de lucru, rezulta ca puterea necesara motorului electric se obtine din relatia:

n₃ = n₂/i_RT = 720,3 / 4 =180 rot/min

Calculul energetic

Puterile primite de arborii ce apartin transmisiei mecanice sunt:

Ø arborele 1:

Ø arborele 2:

Ø arborele 2’:

Ø arborele 3:

Momentele de torsiune transmise de arbori sunt:

Ø arborele 1:

Ø arborele 2:

Ø arborele 2’:

Ø arborele 3:

Predimensionarea arborilor

Solicitarile la care sunt supusi arborii reductorului sunt incovoierea si torsiunea. In calculul de predimensionare a acestora se va lua in consideratie numai torsiunea, iar pentru a tine cont si de incovoiere se vor folosi valori admisibile reduse t_at (uzual t_at = 10÷12N/mm² pentru arborii I si III, iar pentru arborele intermediar II, t_at = 15÷20N/mm²).

Relatia de predimensionare este:

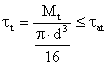
diametrul arborelui I: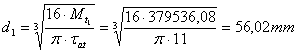

diametrul arborelui II: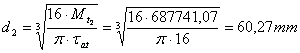

diametrul arborelui II’: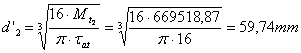

diametrul arborelui III: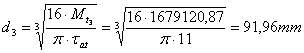

Diametrul capetelor de arbore in functie de momentul transmisibil se alege conform STAS 8724/3-74 tinandu-se seama si de STAS 8724/2-74. Pentru capatul arborelui III, pe care se monteaza cuplajul elastic cu bolturi, se consulta STAS 5982/6-81, iar pentru cuplajul cu flanse STAS 769-73. Lungimile se aleg pentru serie scurta.

arborele I: d₁ = 56mm

toleranta/abateri: m6

l₁ = 82mm

arborele II, II’: d₂ = 60mm = d₂’

toleranta/abateri: m6

l₂ = 105mm

arborele III: d₃ = 95mm

toleranta/abateri: m6

l₃ = 130mm

Proiectarea transmisiei prin curele trapezoidale

Calculul transmisiei prin curele trapezoidale cu arbori paraleli este standardizat: STAS 1163-71.

Marimile de intrare sunt: - puterea la arborele motorului de antrenare:

turatia rotii conducatoare: n₁ = n_M = 1450 rot/min

turatia rotii conduse: n₂ = 720,3 rot/min (sau i_TCT = 1,99)

Al 646i88g egerea tipului curelei

Pe baza nomogramei pentru curele trapezoidale inguste se alege cureaua tip SPB, deoarece conform prescriptiilor se recomanda alegerea tipului de curea de sub linia oblica daca se afla in apropierea frontierelor dintre domenii; plaja de valori ale diametrului primitiv al rotii mici fiind .

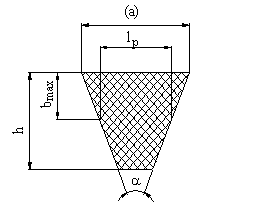
Al 646i88g egerea diametrului primitiv al rotii mici

Aceasta alegere se face in functie de tipul curelei respectandu-se indicatiile din STAS 1164-87; astfel s-a ales .

Fig. 3.1.

Calcularea diametrului primitiv al rotii mari

Calculul se realizeaza cu relatia:

Rezulta: . Standardizam conform STAS 1164-87 si se obtine .

Distanta preliminara intre axe

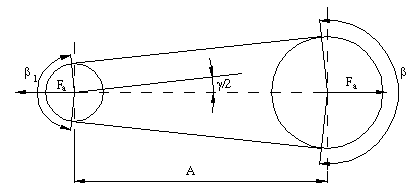
Relatia de calcul:

Fig. 3.2.

Rezulta: A = 640mm.

Unghiul dintre ramurile curelei

Relatia de calcul: .

Rezulta:

Unghiul de infasurare

Q pe roata mica:

Q pe roata mare:

Lungimea primitiva a curelei

Relatia de calcul: Þ L_p = 2497,99mm.

Conform STAS 1164-87: L_p = 2500mm Þ SPB 2500 .

Cu aceasta valoare se recalculeaza A, g b si b₂:

Þ ; prin urmare, A = 640 mm.

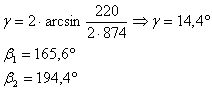
Viteza periferica a curelei

Relatia de calcul: Þ v = 9,14 m/s

Numarul de curele (preliminar)

Relatia de calcul: .

c_f = k_s = 1,3 – coeficient de functionare

c_L = 0,94 – coeficient de lungime

c_b b) – coeficient de infasurare; c_b

P₀ – puterea nominala transmisa de o curea se alege conform STAS 1163-71 pentru conditiile specifice cinematice (n₁) si tipului de curea ales sau folosind relatia de calcul:

Fig. 3.3.

Elementele geometrice ale curelei SPB 2500, conform STAS 7192-83, sunt:

l_p = 14 mm e = 19 ± 0,4 mm

n_min = 4,2 mm a

m_min = 14 mm r = 1,0

f = mm

Calculul lagarului hidrodinamic

Date de intrare:

forta care apasa asupra fusului F_fus = 5060,17 N;

turatia fusului n_II = 487,4 rot/min;

diametrul capatului de arbore: d₂ = 60 mm; diametrul lagarului hidrodinamic se obtine astfel: d_LHD = D ³ d_e + 2÷5 mm, d_e ³ d₂ + 12÷15 mm Þ d_e = 60 +14 = 74 mm Þ d_LHD = = 74 + 4 = 78 mm Þ

diametrul lagarului D = 78 mm.

Date alese:

raportul diametral:

temperaturile de calcul:

jocul relativ:

uleiul: L 46

vascozitatile cinematice ale uleiului corespunzatoare celor cinci valori ale temperaturii considerate sunt:

fig. 4.2.

Fig. 4.1.

Fig. 4.2.

Rezulta doua siruri de valori ale temperaturii de echilibru: t_1e =

t_2e =

Calculul parametrilor pentru temperaturile de echilibru

Grosimea minima a filmului de lubrifiant: , unde reprezinta grosimea minima a filmului de lubrifiant. Totodata d e, unde e - excentricitatea relativa. Rezulta e_i d_i

Debitul hidrodinamic de lubrifiant: , unde - coeficientul debitului hidrodinamic.

In tabelul 3, respectiv tabelul 4, sunt centralizate rezultatele calculelor pentru cele doua valori ale raportului diametral.

t_e, [˚C]

Fig. 4.3.

Fig. 4.4.

Fig. 4.6.

Fig. 4.5.

Fig. 4.7.

Fig. 4.8.

Se considera excentricitatea relativa admisibila e_a = 0,35; temperatura maxima admisibila a lubrifiantului t_a = 60˚C; iar valoarea admisibila a grosimii filmului de lubrifiant s-a stabilit h_a = 6mm.

Jocul relativ la montaj se calculeaza cu relatia: , unde k_d = 11 10^-6 este coeficientul de dilatare a jocului, considerand cuzinetul prelucrat din bronz. Din figura 4.3. se remarca faptul ca pentru nici o valoare y_i adoptata initial nu exista restrictii, astfel incat intervalul rezultat este y I [0,5; 2,5]. Jocul diametral la montaj se calculeaza cu relatia J₂₀ = Dּy. S-au obtinut urmatoarele rezultate:

B/D = 0,5. S-au ales mai multe ajustaje standardizate care sa verifice conditiile: J_{20 min STAS}³ mm si J_{20 max STAS} £ mm. Dintre aceste ajustaje s-a optat pentru H7/e7 caz in care J_{20 min STAS} = 50 mm, iar J_{20 max STAS} = 100 mm, astfel ca y_{20 min STAS}= =0,001087 si y_{20 max STAS} = 0,002174 iar prin interpolarea graficului functiei y = f(y) se obtine y_{min STAS} = 0,001557 si y_{max STAS} = 0,00257 de unde rezulta, mai departe, J_{min STAS} = 71,615 mm si J_{max STAS} = 118,205 mm.

In final, calculam valorile probabile ale caracteristicilor tehnice ale lagarului hidrodinamic:

Prin urmare: B = 23mm

Calculul angrenajului

Predimensionarea angrenajului

Al 646i88g egerea materialelor pentru rotile dintate si a tratamentelor termice sau termochimice

Rotile dintate care fac parte din compunerea reductoarelor de turatie, de orice tip ar fi ele, sunt organe de masini puternic solicitate. Principalele solicitari sunt cea de incovoiere la piciorul dintelui – efort unitar s_F – si solicitarea hertziana la contactul flancurilor – efort unitar s_H, ambele solicitari fiind variabile in timp dupa cicluri de tip pulsator.

Din calculul la tensiune superficiala de contact prin oboseala (pitting) se impune ca cele doua roti sa fie executate din materiale diferite astfel incat flancul dintilor pinionului sa fie mai dur decat flancul dintilor rotii conduse.

Materialele alese sunt:

Predimensionarea angrenajului

Pe baza calculului la solicitare hertziana (pitting) se dimensioneaza diametrul de divizare al pinionului pe conul frontal median :

Verificarea continuitatii angrenarii

Pentru angrenajul conic cu dinti drepti se calculeaza gradul de acoperire al angrenajului cilindric inlocuitor (echivalent) care trebuie sa verifice conditia:

Verificarea rezistentei danturii rotilor dintate

Verificarea dimensionala a danturii rotilor dintate

Calculul reactiunilor. Diagrama de momente incovoietoare si de torsiune

Arborele pinion

Arborele rotii conduse

Document Info

Accesari: 9917
Apreciat:

Comenteaza documentul:

Nu esti inregistrat
Trebuie sa fii utilizator inregistrat pentru a putea comenta

Creaza cont nou

A fost util?

Daca documentul a fost util si crezi ca merita
sa adaugi un link catre el la tine in site

Copiaza codul:
in pagina web a site-ului tau.

eCoduri.com - coduri postale, contabile, CAEN sau bancare

Politica de confidentialitate | Termenii si conditii de utilizare