REZISTENTA SI RIGIDITATEA - ELEMENTELOR DE TIP BARA

REZISTENTA SI RIGIDITATEA - ELEMENTELOR DE TIP BARA

1. ELEMENTE SOLICITATE LA INTINDERE SI COMPRESIUNE CENTRICA

1.1. INTINDEREA SI COMPRESIUNEA CENTRICA. DEFINITIE; EXEMPLE

Intinderea/compresiunea centrica este solicitarea simpla în prezenta careia, în sectiunea transversala, interactiunea este exprimata printr-o pereche de forte axiale (fig.3.1).

fig.3.1.

O pereche de forte echilibrate aplicate pe o bara dreapta de-a lungul axului ei genereaza între punctele de aplicatii întindere/compresiune centrica (fig.3.2). Forta axiala N are intensitatatae P a fiecaruia din cele doua forte exterioare

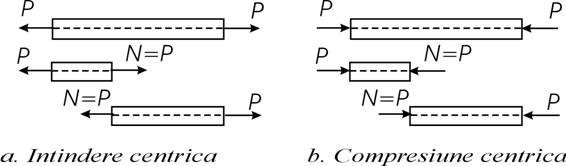
Fig.3.2.

In practica, întinderea/compresiunea centrica este solicitarea caracteristica barelor grinzilor cu zabrele (si în general sistemelor alcatuite din bare drepte articulate la capete, încarcate cu forte în punctele de articulare), numai sub forma de întindere, ea este proprie firelor (drepte, poligonale sau curbe).

1.2. REZISTENTA BARELOR INTINSE/COMPRIMATE CENTRIC

1.2.1. Eforturi unitare pe sectiunea transversala

Studiul geometric (privind modul de deformare). Pe suprafetele laterale ale unei bare drepte cu sectiune dreptunghiulara se traseaza un sistem de linii longitudinale (paralele cu axa) si transversale (perpendiculare pe axa). In regim de solicitare (fig.3.3) liniile transversale se departeaza /aproape (prin translatii) ramânând drepte, paralele între ele si normale pe cele longitudinale.

Fig.3.3.

Observatia corespunde ipotezei Bernoulli (sectiuni transversale plane si normale pe axa ramân plane si normale tot timpul deformarii), confirmând-o (cu putin pe suprafata - vizibila - a barei)

Cu privire la cele doua tipuri de deformatii (liniare si unghiulare) se constata

- lipsa deformatiilor unghiulare ( = 0) caci unghiurile retelei nu se modifica

- prezenta unor deformatii liniare egale în toate fibrele longitudinale ale barei (Dl = const., deci e = const.).

Studiul fizici consemneaza conditia de elasticitate liniara (legea lui Hooke) acceptata în Rezistenta materialelor.

Sinteza studiu geometrica - studiu fizic. Daca g = 0, rezulta t = 0. Daca e = const., rezulta = const. Pe sectiunea transversala, interactiunea punctuala este exprimata prin eforturi unitare normale t egale (uniform distribuite) (fig.3.4).

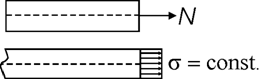
Fig.3.4.

Studiul static. Efortul sectional N si sistemul de eforturi unitare sunt masura aceleasi interactiuni. Studiul static consemneaza echivalenta dintre cele doua moduri de exprimare ale ei:

N = s dA

Sinteza studiu geometric - studiu static. Intrucât s = const.

N = sdA = t_A,

de unde:

s = (3.1).

Marimea efortului unitar s depinde de doi parametri:

- forta axiala N, parametrul global al interactiunii din sectiune, masura solicitarii

- aria A, parametrul geometriei sectiunii transversale.

I.2.2. Proiectarea de rezistenta a sectiunii barelor întinse/comprimate centric

s_a

Relatia contine trei parametri; ei corespund celor trei factori care apar an procesul celor trei factori care apar în procesul proiectarii sectiunii:

- solicitarea, exprimata prin forta axiala N;

- materialul, exprimat prin rezistenta sa admisibila t_a

- geometria suprafetei sectiunii transversale, exprimata prin aria A. 737h72h

Dupa felul în care acestia intervin (ca parametrii cunoscuti sau necunoscuti), proiectaread îmbraca trei aspecte: verificarea, dimensionarea si determinarea capacitatii portante a sectiunii.

Cele trei aspecte ale proiectarii sunt prezentate sintetic în tabelul 3.1 si comentate în continuare.

Parametri

cunoscuti

Parametri necunoscuti

Relatia de calcul

Verificare

N, s_a, A

s_a

Dimensionare

N, s_a

Aria necesara

A_nec

A_nec =

Capacitate portanta

s_a, A

forta capabila

N_cap

N_cap = s_aA

In problemele de dimensionare, dupa stabilirea ariei necesare A_nec, dimensiunile sectiunii (carora le va corespunde aria efectiva Aef) se aleg astfel, încât, indiferent de forma ei , A_ef A_nec.

Capacitatea portanta a unei sectiuni se masoara prin forta axiala - numita forta capabila, N_cap - corespunzatoare unor eforturi unitare egale cu rezistenta admisibila. Rezistenta barei este asigurata daca efortul axial N corespunzator solicitarii (determinat în functie de încarcari) nu depaseste efortul capabil N N_cap.

1.2.2.2. Observatie privind proiectarea barelor comprimate.

Barele comprimate se pot distruge mai înainte cu eforturile unitare (determinate cu raport între forta axiala si aria sectiunii transversale) sa atinga limita de rupere sau de curgere a materialului, prin fenomenul numit flambaj*. In principiu, pericolul flambajului este cu atât mai mare cu cât barele sunt mai svelte. Numai barele robuste (cu lungimea redusa si sectiuni transversale desvoltate) pot fi proiectate la compresiune în conditiile analizate în capitolul de fata.

1.2.3. Concentrari de eforturi

In sectiuni transversale foarte apropiate de punctul de aplicatie a fortei exterioare axiale (fig.3.8) ipoteza lui Bernoulli (a sectiunilor plane.) este infirmata de experiment. Fibrele longitudinale din preajma axei barei, cu deformatii longitudinale mai mari, vor fi mai puternic solicitate;

*) Flambajul va fi analizat pe larg în unul din capitolele urmatoare ale cursului.

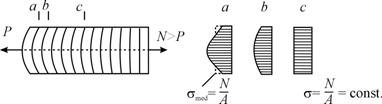
Fig.3.8.

fig.3.8 prezinta distributia eforturilor unitare s în trei sectiuni (a, b, c) aflate la distante diferite de punctul de aplicatii a fortei exterioare.

In sectiuni transversale suficient de departate de punctul de aplicatie a fortelor exterioare, distributia în sectiune a eforturilor unitare nu este influentata de modul de aplicare a acestor forte (principiului Saint-Venant).

Neuniformitatile în distributia eforturilor unitare pe sectiunea transversala apar si la variatii ....ale formei sectiunii (gauri, crestaturi etc.) (fig.3.9).

Concentratiile de eforturi din sectiunile slabite de gauri sau crestaturi au consecinte diferite la materialele casante si ductile.

La materialele casante bara se rupe brusc când "vârful" eforturilor atinge tr (deci la o valoare a efortului mediu mult mai mica decât tr (fig.3.10). La materialele ductile (cu curgere, sau cu deformatii plastice mari) ruperea este un proces îndelungat, care se sfârseste chiar dupa ce, treptat, pe masura ce creste solicitarea, toate eforturile unitare din sectiune ating rezistenta de curgere; distributia eforturilor unitare în câteva faze premergatoare ruperii unei bare alcatuite din material ductil este prezentata în fig.3.11.

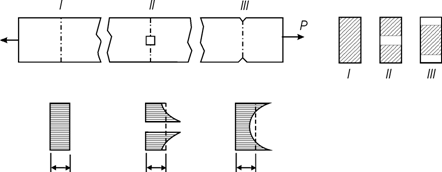
fig.3.10

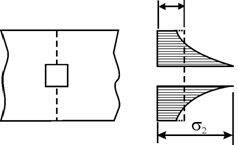
fig.3.10

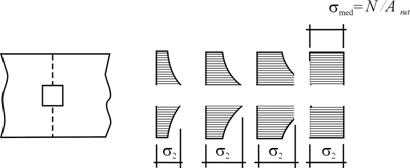
fig.3.11.

1.3. DEFORMATIILE BARELOR INTINSE/COMPRIMATE CETRIC

1.3.1. Calculul deformatiilor

Intre deformatii si eforturi exista legatura liniara exprimata de legea lui Hook s = Ee; de aici se deduce expresia formatiilor specifice liniare e

e =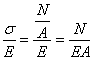

Deformatia specifica liniara e este proportionala cu solicitarea (N) si invers proportionala cu factorul de rigiditate la întindere /compresiune (produsul EA); acesta, la rândul lui, depinde de doua categorii de parametri: modulul de elasticitate E (care exprima rigiditatea materialului) si aria suprafetei sectiunii transversale A (care exprima rigiditatea sectiunii).

Cum e reprezinta deformatia unitatii de lungime, deformatia întregii unitati de lungime, deformatia întregii bare (alungirea sau scurtarea Dl) e proportionala cu lungimea l:

Dl = el (3.3)

Dl = (3.4)

1.3.2. Efectul static al variatiilor de temperatura în bare

O bara libera, cu lungimea l, supusa unei variatii de temperatura Dt^o se dilata/contracta (alungeste/scurteaya) cu cantiatea.

Dl_t = Dt^o a l (3.5)

unde a este coeficientul de dilatatie termica al materialului; pentru otel,

a

Aplicatie. La o variatie de temperatura de 30^o, o bara de otel de 8 m lungime se alungeste/scurteaza cu

Dl_t = 30 . 1,2 . 10^-5 . 8000 mm = 2,88 mm

Daca dilatatia/contractia barei este împiedicata de legaturile acesteia în sistem, în bara apar eforturi t_t de compresiune/întindere corespunzatoare alungirii/scurtarii blocate (ca si cum eforturi axiale de compresiune N ar constrânge bara dilatata cu cantitatea Dl_t sa revina la pozitia initiala printr-o scurtare Dl_N egala

Dl_t = Dl _N;

Dt^o . a . l = ,

de unde

s_t = = Dt . a . E (3.6)

Aplicatie. Pentru bara din exemplul precedent, blocarea deformatiilor de dilatare/contractie genereaya eforturi unitare care consuma mai mult de jumatate din reyistenta admisibila a materialului:

s_t = 30 . 1,2 . 10^-5 . 2,1 . 10⁶ = 755 Kgf/cm²

De remarcat ca în expresia eforturilor unitare (3.6) nu intervine geometria barei (nici aria sectiunii transversale, nici lungimea). Eforturile nu pot fi moderate prin dimensionare, ci printr-o conformare de ansamblu a structurii care sa permita deformatii libere.

In sistemul static determinate (cu numar minim de legaturi) deformatiile de dilatare/contractie se produc liber (fig.3.12.a), deci fara consecinte asupra starii de efort din bare.

Legaturile suplimentare ale sistemelor static nedeterminate îngradesc libertatea de deformare, generând în bare eforturi (fig.3.12.b).

fig.3.12

2.1. FORFECARE PURA. DEFINITIE; EXEMPLE

Forfecarea pura este solicitarea simpla în prezenta careia, în sectiunea transversala, interactiunea este exprimata printr-o pereche de forte taietoare (fig.3.14).

Fig.3.14.

Doua forte P, paralele, egale si de sens contrar, actionând, la distanta neglijabila între ele, normal pe axul barei, genereaza forfecare pura (fig.3.15). Forsa taietoare T are intensitatea P a fiecareia din cele doua forte exterioare.

Fig.3.14.

2.2. CADRUL PROBLEMEI

Sub forma pura (sau macar aproximativ) solicitarea apare rar.

In cele ce urmeaza studiul se limiteaza la cazane curent al forfecarii pieselor cu sectiuni transversale mici (mituri, buloane, cordoane de sudura , etc. - folosite la îmbinarile elementelor din metal) la care efectul unor solicitari secundare este redus.

2.3. APROXIMATIV SI IPOTEZE SIMPLIFICATOARE

A. Chiar si în cazul din fig.3.15 forfecarea lor însotita la încovoiere; momentul cuplului este mic însa si se neglijeaza.

B. La forfecarea pieselor cu suprafata sectiunii redusa se admite ca forta taietoare este rezultanta unor eforturi elementare tangentiale paralele, a caror masura este un efort unitar t cu intensitate constanta.

2.4. EFORTURI UNITARE PE SECŢIUNEA TRANSVERSALA

In conditiile ipotezei B facuta în paragraful precedent (t = const),

T = A;

de unde,

t = (3.7)

2.5.1. Descrierea imbinarii

O îmbinare realizeaza legarea elementelor într-un ansamblu indeformabil.

Imbinarilse cu nituri solicitate axial blocheaza deplasarile relative în lungul unui ax comun celor doua elemente. Fig.3.16 prezinta o astfel de îmbinare.

Fig.3.16.

Niturile sunt piese din otel (rezistenta otelului nitului este putin inferioara celei a otelului pieselor care se îmbina) cu forma din fig.3.17.a. Imbinarea se realizeaza prin introducerea niturilor încalzite la rosu în gauri date în prealabil si formarea, prin baterie, a celui de-al doilea cap (fig.3.17.b.).

fig.3.17.

2.5.2. Proiectarea îmbinarilor cu nituri

2.5.2.1. Modul de lucru. Sub actiunea fortelor P, de sens contrar, care solicita îmbinarea, cele doua elemente au tendinta de a luneca relativ (fig.3.18). Ca urmare, îmbinarea se poate distruge în doua feluri:

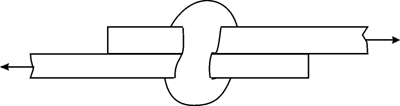
fig.3.18

- prin forfecarea tijei sitului în sectunea transversala din dreptul planului de separatie a celor doua elemente;

- prin strivirea tijei pe suprafata de contact dintre tija si peretii gaurii de nit.

"Transportul" fortelor prin îmbinare (adica efectul lor pe suprafata forfecata si pe suprafata strivita) este reprezentat în fig.3.19 prin forte interioare de legatura.

fig.3.19.

Se remarca echilibrul care controleaza parametrii tuturor acestor forte.

Forta pe care o poate transmite îmbinarea prin intermediul unui singur nit (numita rezistenta nitului) depinde de rezistenta la forfecare Rf (în sectiunea transversala a tijei) si de rezistenta la strivire Rs (pe suprafata de contact dintre dija si elementele îmbinate.

2.5.2.2. Rezistenta nitului la forfecare. Capacitatea de rezistenta în sectiunea transversala a tijei depinde de aria sectiunii forfecate, Af, si de rezistenta admisibila la forfecare, t_af, a materialului tijei. In baza relatiei (3.7);

Rf = Af . af

Rf = af, (3.8)

unde d este diametrul nitului.

Pe baza experimentale, se considera

ta,

unde ta este rezistenta admisibila la compresiune a materialului elementelor care se îmbina. Pentru elemente din OL37 (cu nituri din OL34), af = 0,8 x 1500 = 1200 Kgf/cm².

2.5.2.3. Rezistenta nitului la strivire. Presiunile reciproce dintre tija si peretii gaurii au distributia neuniforma din fig.3.2 pentru simplificarea calculelor, volumul matizat, având o distributie uniforma, pe edeala, de forma dreptunghiulara, a unui plan diametral (fig.3.20.b).

fig.3.20

In aceste conditii simplificatoare, capacitatea de rezistenta la strivire Rs depinde de aria sectiunii strivite.

si de rezistenta admisibila la strivire de peretii gaurii de nit tag. Daca elementele care se îmbina au grosimi diferite (t1ft2), aceeasi forta P se distribuie pe suprafete cu arii diferite; eforturile unitare de strivire fiin mai mari pe piesa mai subtire, în determinarea ariei As se va considera tmin :

Rs = dt_min t_ag (3.9)

Rezistenta admisibila la strivire t_ag se considera dat în raport cu rezistenta admisibila t_a a materialului elementelor de îmbinat:

ag = 2 a

Pentru OL37, ag = 2 x 1500 = 3000 Kgf/cm²

2.5.2.4. Rezistenta nitului. Rezistenta nitului (forta P pe care o poate transmite îmbinarea prin intermediul unui singur mit), R, este cea mai mica dintre valorile Rf si Rs definite anterior.

2.5.2.5. Rezistenta nitului cu mai multe sectiuni de forfecare. La o îmbinare de trei elemente (fig.3.21) forta P se transmite prin forfecare a doua sectiuni. Rezistenta nitului la forfecare Rf se va dubla, caci numai jumatate din forta P trebuie echilibrata de eforturile tangentiale dintr-o sectiuune transversala a tijei. La limita de rezistenta,

= Af . af,

de unde

Rf = 2 af

Pentru mai multe sectiuni de forfecare, daca nf este numarul lor

Rf = ng af (3.10)

La determinarea rezistentei nitului la strivire, interactiunile ce apar la contactul tijei cu elementele cu tendinte de lunecare opuse

Fig.3.21.

se considera separat; strivirea maxima apare pe suprafeta minima si aceasta este suprafata care intervine în determinarea rezistentei Rs

Rs = d (St) min   ag (3.11)

unde (St) min este suma minima a grosimilor elementelor care tind sa se deplaseze în acelasi sens.

2.5.2.6. Determinarea numarului de nituri. La îmbinarea elementelor solicitate la întindere sau compresiune centrica se admite ca forta transmisa prin îmbinare se repartizeaza în mod egal tuturor niturilor. In aceasta ipoteza, numarul necesar de nituri, n, se determina împartind forta P care "traverseaza" îmbinarea la rezistenta R a unui singur mit:

n = (3.12)

Diametrul nitului (care intervine în calculul rezistentei sale) se alege în functie de grosimea celui mai subtire element din pachet, pe baza unor prevederi constructive cuprinse în standarde (cu aproximatie, d = 2t). Tot standardele precizeaza reguli privind propozitia niturilor în îmbinare.

Desi calculul îmbinarilor nituite are un caracter conventional (fiind condus pe baza mai multor ipoteze simplificatoare), rezultate obtinute corespund capacitati reale de rezistenta, întrucât rezistentele admisibile acceptate sunt determinate, experimental, tocmai prin ruperea unor astfel de îmbinari.

2.6. COMPORTAREA IMBINARILOR CU BULOANE

La îmbinarea elementelor metalice se folosesc doua categorii de buloane:

- buloane obisnuite (buloane brute, cu tija neprelucrata , care se introduc liber în gauri cu diametrul mai mare si buloane pasuite, cu tija prelucrata, introduse fortat în gauri de acelasi diametru);

- buloane de înalta rezistenta, pretensionate la montaj.

Imbinarea cu buloane obisnuite se comporta la foc cu îmbinarea cu nituri (cu rezistente admisibile identice celor folosite la îmbinarile cu nituri - în cazul buloanelor pasuite - sau cu rezistente ceva mai mici - în cazul buloanelor brute).

La îmbinarea prin buloane de înalta rezistenta, transmiterea fortelor prin îmbinare se bazeaza pe frecarea dintre elementele strivite puternic prin intermediul buloanelor. In aceste conditii bulonul este solicitat la întindere.

2.7. PROBLEME DE FORFECARE LA IMBINARI SUDATE SOLICITATE AXIAL

2.7.1. Descriere

Solidarizarea elementelor sudate se realizeaza cu material topit sub forma unui cordon.

Dupa pozitia relativa a elementelor care se îmbina, rândurile se împart în doua categorii:

- suduri în adâncime, folosite la îmbinarea cap la cap a doua elemente în prelungire (fig.3.22);

- suduri în relief sau de colt, executate la elemente suprapuse (fig.3.23).

fig.3.22   fig.3.23

2.7.2. Proiectarea îmbinarilor sudate

. Se constata experimentul ca sudurile în relief se distrug prin forfecarea cordonului de sudura în planul sau bisector; fig.3.24 prezinta ruperea unui cordon lateral, iar fig.3.25 - ruperea unui cordon frontal.

fig.3.24 fig.3.25

2.7.2.2. Conditii de rezistenta. Capacitatea de rezistenta a cordonului de sudura (forta taietoare din planul suprafata forfecate corespunzatoare unei distributii de eforturi unitare egale cu rezistenta admisibila) depinde de aria forfecata As si rezistenta admisibila a materialului sudurii, as, admitând ca eforturile tangentiala t se distribuie uniform pe suprafata forfecata, capacitatea cordonului este

t_as A

Se considera ca rezistenta admisibila la forfecare a cordonului de sudura tas este doua treimi din rezistenta admisibila t_a a materialului pieselor îmbinarii; pentru OL 37, t_as = 2/3 . 1500 = 1000 Kgf/cm².

Suprafata forfecata a cordonului de sudura este un dreptunghi cu latura mica egala cu grosimea cordonului, de sudura si latura mare egala cu lungimea cordonului de sudura. Grosimea de calcul, a, se considera, acoperitor, egala cu înaltimea triunghiulara isoscel înscris în forma sectiunii transversale prin cordon (fig. 3.2.b) : a 0,7 b; ea corespunde sectiunii forfecate cu aria (deci si capacitate de rezistenta) minima. Lungimea de calcul, l, rezulta din lungimea efectiva ls a cordonului prin

scaderea zonelor de capat (fiecare cu o lungime aproximativ egala cu grosimea de calcul a) unde sudura este de slaba calitate : l = ls - 2a. Cu observatiile de mai sus:

As = Sl . a

Alegând grosimea unui cordon (se recomanda b t_min), rezulta lungimea sa, astfel încât capacitatea însumata a tuturor cordoanelor forfecate sa fie superioara fortei axiale transmise prin îmbinare.

x

Sudurile în adâncime lucreaza la întindere, si sunt solicitate la eforturi normale t

3. ELEMENTE SOLICITATE LA INCOVOIERE PURA

3.1. DEFINITIE; EXEMPLE

Incovoierea pura este solicitarea simpla în prezenta careia, în sectiunea transversala interactiunea este exprimata printr-o pereche de momente încovoietoare (vectori cuplu cuprinsi în planul sectiunii).

Sub forma pura, încovoierea apare iar. Doua cazuri sunt furnizate la situatiile particulare de încarcare din fig.3.27; tronsoanele 1 - 2 ale celor doua grinzi (unde T=0) sunt solicitate la încovoiere pura.

De obicei, încovoierea apare însotita de forfecare; sub aceasta forma, tipica grinzilor va fi tratata în subcapitolul 4.

In functie de directia vectorului moment încovoietor fata de axele principale de inertie ale sectiunii transversale, se deosebesc urmatoarele doua cazuri:

- încovoiere pe doua directii sau încovoiere oblica (cazul general), când directia vectorului cuplu este oarecare fata de directia axelor;

- încovoiere pe o directie sau încovoiere simpla (cazul particular), când directia vectorului cuplu coincide cu directia uneia din axe.

Grinzile cu sectiuni simetrice (în raport cu cel putin o axa), încarcate cu forte în planul de simetrie longitudinal, sunt solicitate la încovoiere pe o singura directie (fig.3.28). Este cazul cel mai des întâlnit în practica si el va fi studiat în continuare.

O pava de acoperis (fig.3.29) este solicitata la încovoiere oblica (pe doua directii) ; dar fiecare din cele doua componente Mx si My (pe directiile principale de

fig.3.28

inertie) este masura unei solicitari de încovoiere simpla.

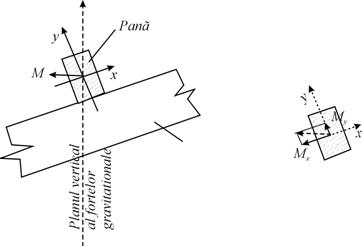
fig.3.29

3.2. REZISTENTA BARELOR INCOVOIATE

EFORTURI UNITARE PE SECTIUNEA TRANSVERSALA. FORMULA LUI NAVIER

Studiul geometric. Pentru a evidentia modul de deformare, pe suprafetele laterale ale unei bare drepte cu sectiune dreptunghiulara se traseaza un sistem de linii longitudinale (paralele cu axa) si transversale (perpendiculare pe axa) (fig. 3.30.a). In regim de solicitare (fig.3.30.b) liniile longitudinale se curbeaza în liniile transversale se curbeaza în liniile transversale se rotesc, ramânând - în spiritul ipotezei lui Bernoulli - drepte si normale pe cele longitudinale.

Cu privire la cele doua tipuri de deformatii (liniare si unghiulare) se constata:

- lipsa deformatiilor unghiulare (g = 0), caci unghiurile retelei nu se modifica;

- prezenta unor deformatii liniare pe directia axei barei.

In zonele cu încovoiere pozitiva (cazul din figura) fibrele longitudinale de la partea inferioara se alungesc, iar cele de la partea superioara se scurteaza. Se intuieste prezenta unui plan de fibre (fibre neutre) care se curbeaza fara

a-si modifica lungimea; intersectia dintre acest plan si planul sectiunii transversale se numeste axa neutra.

Doua sectiuni aflate la distanta elementara dz se rotesc cu unghiul elementar d (fig.3.31.a); pe desen s-au pus în evidenta fibra neutra AB cu lungimea neschimbata (AB = dz) si raza de curbura a fibrei neutre (OA = OB = ).

Variatia de lungime a unei fibre oarecare (MNN') aflata la cota y' fata de firbra neutra este pusa în evidenta în fig. 3.31.b prin segmentul NN'. Din asemanarea triunghiurilor OAB si BNN' rezulta:

sau

;

primul raport (dintre alungirea fibrei si lungimea ei initiala) este deformatia specifica e si relatia de asemanare devine:

e = >'; (3.13)

deformatiile specifice e, nule în dreptul axei neutre, variaza liniar pe înaltimea sectiunii transversale (fig.3.32.a).

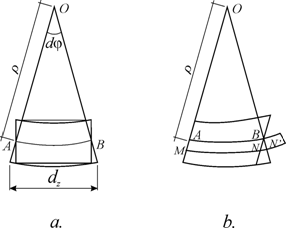
fig.3.31

Studiul fizic consemneaza conditia de elasticitate liniara (legea lui Hooke) acceptata în Rezistenta materialelor:

s = Ee

t = 6g

Sinteza studiu geometric - studiu fizic. Daca g t = 0. Pe sectiunea transversala, interactiunea este masurata numai prin eforturi unitare normale t. Introducând relatia (3.13) în legea lui Hooke, rezulta:

s = E y'; (3.14)

ca si deformatiile specifice e, eforturile unitare normale t, nule în dreptul axei neutre, variaza liniar pe înaltimea sectiunii transversale (fig.3.32.b si 3.32.c). Axa neutra împarte sectiunea în doua zone: una comprimata si alta întinsa (fig.3.32.d).

Studiul static consemneaza echivalenta dintre cele doua moduri de exprimare a interactiunii: prin eforturi

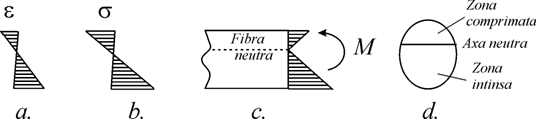
a - diagrama de distributie a deformatiilor specifice e

b - diagrama de distributie a eforturilor unitare normale

c - masura interactiunii: prin eforturi unitare normale si prin momentul încovoietor M

d - sectiunea transversala si axa neutra

Fig.3.32

sectionale (Mx 0; N = 0) si prin eforturi unitare ( ) (fig.3.33):

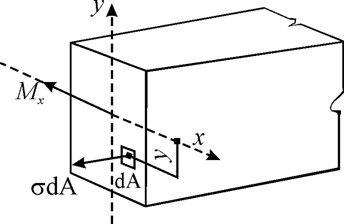
Fig.3.33

N = S_A td_A = 0; (3.15)

Mx = S_A td_A . y   (3.16)

Sinteza studiu geometric - studiu fizic - studiu static. Cu (3.24), prima relatie de contravalenta devine

N = E . S_A y'd_A

adica

S_A y'd_A = 0

Integrala reprezinta un moment static (al suprafetei sectiunii transversale fata de axa neutra a sectiunii); din faptul ca e nul, rezulta ca axa neutra trece prin centrul de greutate al suprafetei sectiunii; ea coincide cu axa x, motiv pentru care y si y' masoara aceeasi distanta.

Cu (3.14) a doua relatie de echivalenta devine:

Mx = E S_A y²dA

sau

Mx = E S_A Ix, (3.17)

unde Ix reprezinta momentul de inertie ale suprafetei sectiunii în raport cu axa x. Revenind la relatia (3.14), din care rezulta

E

(3.17) devine

Mx =

t = (3.18)

Expresia (3.18) cunoscuta sub numele de formula lui Navier precizeaza marimea efortului unitar normal t într-un punct M situat la distanta y fata de axa neutra (fig.3.34).

Fig.3.34

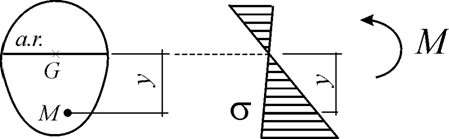
3.2.2. EFORTURI UNITARE MAXIME

Valorile maxime ale eforturilor unitare se dezvolta în fibrele extreme (cele mai departate de axa neutra). Daca Ymax este distanta de la fibra extrema la axa neutra rezulta

t_max = Y_max

t_max =

unde la numitor apare expresia modulului de rezistenta Wx al suprafetei sectiunii în raport cu axa netura x (2.9). Cu aceasta observatie,

t_max = (3.19)

Marimea efortului unitar maxim deprinde de doi parametri:

- momentul încovoietor M, parametrul global al interactiunii din sectiune, masura solicitarii;

- modulul de rezistenta W, parametrul geometriei sectiunii transversale.

3.2.3. Trei forme ale interactiunii sectionale

Rezultanta fortelor interioare de legatura de pe zona întinsa, Fi, si comprimata, Fc, sunt doua forte egale si de sens contrar (fig.3.35); ele formeaza un cuplu al carui

Fig.3.35.

moment este echivalent cu momentul încovoietor M. Momentul încovoietor M, cuplul fortelor Fc si Fi (rezultantele fortelor interioare de legatura) si sistemul de forta interioare de legatura cu distributie continua (a caror masura sunt eforturile unitare normale s) reprezinta trei forme ale aceleasi interactiuni.

Proiectarea de rezistenta a sectiunii barelor încovoiate

Conditii de rezistenta. Verificare; dimensionare; capacitate portanta

Conditii de rezistenta impusa de metoda de calcul a rezistentelor admisibile (1.1) devine

s_a (3.20)

Relatia contine trei parametri; ei corespund celor trei factori care intervin în procesul proiectarii sectiunii barelor încovoietoare:

- solicitarea, exprimata prin momentul încovoietor M;

- materialul , exprimat prin rezisnteta sa admisibila s_a

- geometria suprafetei sectiunii transversale, exprimata prin modulul de rezistenta W, determinat în raport cu axa neutra (axa principala centrala de inertie ce coincide cu suportul vectorului moment).

Dupa felul în care acestia intervin (ca parametri cunoscuti sau necunoscuti), proiectarea îmbraca trei aspecte; verificarea rezistentei sectiunii, dimensionarea sectiunii si determinarea capacitatii portante a sectiunii.

Cele trei aspecte ale proiectarii sectiunii sunt sintetic în tabelul 3.2.

Parametrii cunoscuti

Parametrii necunoscuti

Relatia de calcul

Verificare

M, s_a,W

s_a

Dimensionare

M, s_a

modulul de rezis- tenta necesar W_nec

W_nec =

Capacitate portanta

s_a, M

momentul capabil M_cap

M_cap = s_aW

La materialele cu rezistente admisibile diferite la întindere si la compresiune (de ex. fonta) sunt necesare doua verificari: una în zona întinsa, alta în zona comprimata a sectiunii.

In problemele de dimensionare dimensiunile sectiunii se aleg astfel, încât

W_ef W_nec,   (3.21)

unde W_ef este modulul de rezistenta efectiv (al sectiunii propuse prin proiectare). Pentru bare cu sectiune circulara,

W_nec

de unde rezulta diametrul. Pentru bare cu sectiunea dreptunghiulara,

W_nec;

relatia contine doua necunoscute - b si h; determinarea lor se face propunând fie una din ele, fie cu anumit raport (orientativ) între ele. Pentru barele cu sectiuni stadardizate care se confectioneaza într-un numar limitat de tipuri (cazul profilelor laminate din otel, sau al majoritatii grinzilor din lemn cu sectiune dreptunghiulara), sectiunea rezulta direct prin compararea valorii W_nec cu valoarea W_ef din tabelele de caracteristici ale fiecarui tip de sectiune. Pentru sectiuni de alte forme, dimensionarea se face prin încercari, verificând relatia (3.2) pentru diferite sectiuni propuse.

Capacitatea portanta a unei sectiuni se masoara prin momentul încovoietor (numit moment capabil, Mcap), caruia îi corespunde un efort unitar maxim egal cu rezistenta admisibila. Rezistenta barei în sectiunea analizata este asigurata daca momentul încovoietor M generat de încarcare nu depaseste momentul capabil: M M_cap.

Verificarea si dimensionarea cu momentul încovoietor maxim.

3.2.4.2. Criterii de conformare. Sectiuni rationale; randamentul sectiunii.

Criteriul de rezistenta W_nec = M/s_a aplicat la dimensionarea sectiunii ofera o infinitate de solutii. El poate fi satisfacut de sectiuni cu forme si arii diferite; urmând reducerea consumului de material se prefera formele cu arie minima. Pe de alta parte, la arii egale, forme diferite asigura capacitati diferite; forma rationala va corespunde capacitatii maxime.

Capacitatea sectiunii (exprimata ca moment al cuplului rezultantelor fortelor interioare de legatura) este proportionala cu valoarea - egala - a celor doua rezultante (Fc = Fi) si cu bratul lor de pârghie Z (fig.3.36).

A. Cresterea capacitatii sectiunii prin cresterea valorii rezultantelor fortelor interioare de legatura

Suprafata sectiunii nu este solicitata uniform. Cu cât o parte cât mai mare din suprafata sectiunii se va afla în zonele cele mai solicitate (cu eforturi unitare mari), cu atât rezultanta fortelor interioare de legatura (ca suma a produselor dintre efortul unitar si elementul de arie) va fi mai mare.

Pentru o sectiune dreptunghiulara cu aria A,

Fc = Fi = s_a Fc = Fi = s

Pentru o sectiune fictiva, ideala, cu aceeasi arie, cu suprafata concentrata în mod simetric la cele doua extremitati (acolo unde toate eforturile unitare ating rezistenta admisibila ) (fig.3.37.b), rezultanta va fi dubla;

Fc = Fi = s_a

Fig.3.36

Fig.3.37

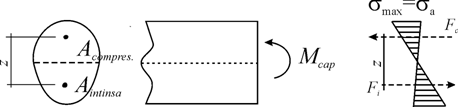
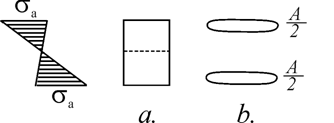
B. Cresterea capacitatii sectiunii prin cresterea bratului de pârghie.

Este evident ca bratul creste odata cu cresterea înaltimii sectiunii.

Dar cresterea înaltimii h este limitata de diferite considerente (functionale, estetice, etc.). La înaltimea constanta, bratul creste (ca si rezultantele fortelor interioare de legatura) tot prin îndepartarea materialului axa neutra.

Pentru sectiunile de forma dreptunghiulara, indiferent de proportiile lor,

Z = h (3.22)

Bratul de pârghie maxim, z = h, corespunde sectiunii ideale cu suprafata concentrata la cele doua extremitati.

Iata acum, pentru cele doua tipuri de sectiune luate ca repere în exemplele precedente, valoarea capacitatii portante, Mcap, ca produs între rezultantele fortelor interioare de legatura si bratul de pârghie:

- pentru sectiunea dreptunghiulara,

s_a . h = s_a

- pentru sectiunea ideala,

s_a . h = s_a

Daca sectiunile au aceeasi arie, aceeasi înaltime si sunt alcatuite din aceleasi material, capacitatea sectiunii ideale este de trei ori mai mare decât capacitatea sectiunii de forma dreptunghiulara.

O sectiune nationala tinde, prin conformarea ei, catre forma ideala descrisa mai sus. Aceasta forma constituie reperul sectiunilor de tip I sau U ale parapetelor laminate sau ale grinzilor din otel "cu sectiune compusa", confectionate prin sudare sau solidarizarea cu nituri (fig.3.38).

Fig.3.38

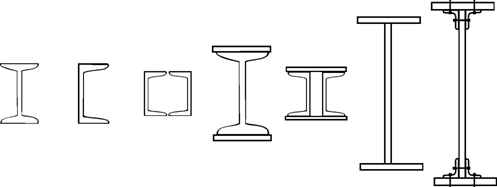
Este de semnalat si tipul de grinda metalica "expandata", realizata prin sudarea, în poziâie decalata, a doua jumatati de inima taiate dupa o linie poligonala (fig.3.39).

Fig.3.39

Caracteristica geometrica a suprafetei sectiunii care determina nemijlocit capacitatea portanta este modelul de rezistenta W:

s_a

capacitatea este direct proportionala cu modulul de rezistenta.

In legatura cu sectiunea ideala se defineste modulul de rezistenta ideal:

W_ideal =

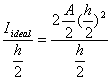
W_ideal =

Raportul dintre modulul de rezistenta W al unei sectiuni de forma data si modulul de rezistenta ideal reflecta raportul dintre capacitatile portante ale celor doua sectiuni si se numeste randament al sectiunii:

r = (3.23)

Randamentul sectiunii dreptunghiulare este doar 1/3. Randamentul sectiunii profilelor laminate de tip I si U este aproape 2/3, deci dublu.

3.3. DEFORMAREA BARELOR INCOVOIATE

3.3.1. Parametrii deformarii

Parametrii fundamentali (privind deformatia unui volum elementar)

Parametrii care definesc deformarea unui volum elementar sunt deformatia specifica liniara e si de formatia specifica unghiulara g. In elementele solicitate de încovoiere pura, deformatiile unghiulare sunt nule (g = 0) iar deformatiile liniare e, masurate în lungul axului barei, variaza liniar pe înaltimea sectiunii, cu valori nule în dreptul axei neutre (care o împarte în doua zone: una comprimata, cu fibre scurtate, alta întinsa, cu fibre alungite) (fig.3.40).

Parametrii globali (privind deformarea unui tronson elementar de baza. Parametrii globali sunt raza de curbura barei 1/s, rotirea elementara dr (rotirea elementara a doua sectiuni aflate la distanta elementara dz), rotirea specifica cu (rotirea relativa a doua sectiuni aflate la distanta unitara( (fig. 3.41).

Fig.3.41.

Parametrii practici ai deformarii (privind deformatiile absolute ale bazei). Parametrii practici ai deformarii sunt rotirea j (rotirea absoluta a unei sectiuni) si sageata v (deplasarea, pe directia normala la axa barei, a centrului de greutate al unei sectiuni ) (fig.3.42).

Fig.3.42 Fig.3.43

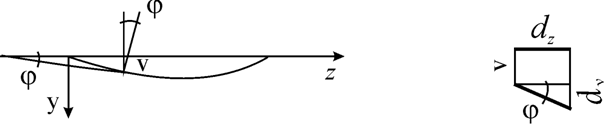
3.3.1.4. Relatii între parametrii deformarii. Deformatia specifica e este proportionala cu curbura 1/r (conform relatiei 3.24):

e =

Din fig.3.41 se deduce relatia dintre parametrii globali ai deformarii:

(3.24)

Din fig.3.43, care prezinta un tronson elementar de bara în doua pozitii - înainte si dupa deformarea barei, se deduce relatia dintre cei doi parametri practici ai deformarii:

(3.25)

De unde, prin derivare, considerând si relatia (3.24), rezulta:

care face legatura între toti parametrii deformarii.

3.3.2. Determinarea parametrilor deformarii

3.3.2.1. Relatii între parametrii statici si parametrii geometrici ai raspunsului si schema relatiilor; expresia curburii.

=

t

Parametrii s eE

raspunsului

e = y

geometrici parametrul

global 1/r

Introducând în legea lui Hooke (relatia dintre parametrii fundamentali ai raspunsului - t si e) expresiile lor în functie de parametrii globali M si 1/r, rezulta

(3.27)

Curbura barei este proportionala cu solicitarea, masurata prin momentul încovoietor M. Produsul EI, numit factor de rigiditate la incovoiere introduce în expresia curburii atât rigiditatea materialului, prin modulul de elasticitate E, cât si rigiditatea formei sectiunii, prin momentul de inertie I al suprafetei sectiunii în raport cu axa neutra.

De remarcat faptul ca expresia rotirii specifice

w = ,

care deriva din (3.27) si (3.24), are aceeasi structura cu expresia alungirii/scurtarii specifice e la solicitarea de întindere/compresiune centrica (3.2).

3.3.2.2. Ecuatia axei elastice a barei (a axei bazei în regim de deformare liniar - elastic) Cu (3.2b) relatia (3.27 devine

(3.28)

Intrucât pentru momente încovoietoare pozitive (în prezenta carora sagetile sunt pozitive) concavitatea barei este îndreptata spre sensul negativ al axei v, derivata a doua a sagetii trebuie sa fie negativa, cu aceasta observatie, relatia (3.28) devine

(3.29)

Fig.3.44

3.3.2.3. Determinarea rotirii si sagetii prin integrarea analitica a ecuatiei axei elastice. prin integrarea succesiva a ecuatiei (3.29) se obtin expresiile rotirii,

j(z) =

si sagetii v(z)

Urmatoarea aplicatie va urmari stabilirea ecuatiei elastice a barei si determinarea expresiilor rotirii si sagetii pentru o consola încarcata cu o forta concentrata la extremitatea ei (fig.3.45)

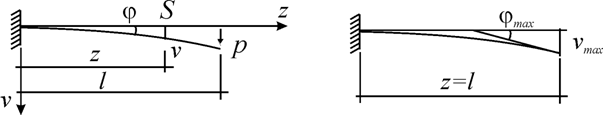
Fig.3.45 Fig.3.46

Intr-o sectiune S, la distanta z de încastrare, momentul încovoietor are expresia

M (z) = - P (l - z) (3.30)

Cu (3.30) ecuatia axei elastice devine

(l - z)

Integrând de doua ori, se obtine pe rând :

j = (l_z - ) + C_1,

v = + C_iz + C₂

Pentru z = 0 (în încastrare), si rotirea si sageata sunt nule; de unde, C1 = 0 si C2 = 0. Epresiile generale ale rotirii si sagetii sunt deci:

j(z) =

v(z) =

La capatul liber al consolei (pentru z = l), si sageata si rotirea sunt maxime (fig.3.46):

j_max = (3.31)

v_max = (3.32)

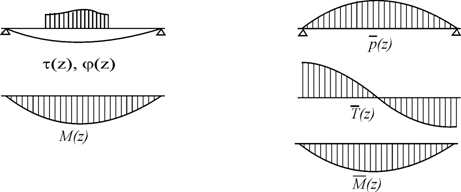
3.3.2.4. Determinarea rotirii si sagetii prin metoda grinzii conjugate (fictive). In paralel cu grinda reala (fig.3.49), pentru care urmeaza sa se determine parametrii deformarii j si v, se considera   o grinda fictiva, conjugata celei reale (fig.3.50).

Intre sageata v, rotirea j si momentul încovoietor M (parametrii ai situatiei reale) exista relatia, dedusa anterior.

(3.33)

Intre încarcarea p, forta taietoare T si momentul încovoietor M (parametri ai situatiei fictive) exista relatia dedusa în partea a III-a a cursului.

Daca

p = ;

si

iar în conditiile în care constantele de integrare sunt nule,

v = M (3.34)

si

j = T (3.35)

Ceea ce înseamna ca, în orice sectiune a grinzii reale, sageata si rotirea sunt egale cu momentul încovoietor si forta taietoare din sectiunea corespunzatoare a unei grinzi fictive, conjugata celei reale, supusa încarcarii

p (z) =

Anularea constantelor de integrare este conditionata de un anume mod de rezemare a grinzii fictive în functie de rezemarea grinzii reale. Unei încastrari a grinzii reale (cu j = 0 si v = o) în corespunde în grinda fictiva un capat liber (caci numai într-o astfel de situatie si T si M sunt nule); unui capat liber al grinzii reale (cu j 0 si v 0) îi corespunde în grinda fictiva o încastrare (care asigura F 0 si M 0) ; unui reazem simplu sau articulat (cu j 0 si v = 0) la capatul grinzii reale îi corespunde în grinda fictiva acelasi tip de reazem (pentru care F 0 si M = 0). Modul de rezemare a grinzii fictive este sintetizat în tabelul de mai jos.

Grinda reala

Grinda fictiva

jmax = Tmax = M max = vmax = Mmax = Aceleasi rezultate s-au obtinut si prin integrarea analitica a ecuatiei axei elastice, în cadrul aplicatiei de la punctul 3.3.2.3. 3.3.2.5. Formule uzuale pentru cazuri particulare de rezemare si încarcare. Tabelul urmator prezinta expresiile actiunii maxime si sagetii maxime pentru grinda simpla rezemata si grinda încastrata în doua situatii particulare de încarcare. jmax vmax 3.3.3. Proiectarea rigiditatii barelor încovoiate Functionarea corecta a unei constructii este conditionata si de o anume rigiditate a elementelor sale. Deformatii mari dauneaza exploatarii, chiar daca rezistenta este asigurata. Proiectarea rezistentei trebuie dublata de proiectarea rigiditatii. Conditia de rigiditate care se impune de obiecei urmareste limitarea sagetilor. Cu o sageata mare ste perceptibila numai în raport cu o deschidere relativ mica, conditia de serie sub forma (3.36) unde f este sageata maxima, l - deschiderea iar k - un coeficient care depinde de functiunea elementului, de importanta sa etc. Valorile sale curente sunt cuprinse între 200 si 400. 4.1. DEFINITIA SOLICITARII. EXEMPLE Incovoierea cu forte taietoare este o solicitare compusa în prezenta careia, în sectiunea transversala, interactiunea este exprimata prin doua tipuri de efort sectional: moment încovoietor si forta taietoare. Incovoierea cu forte taietoare este tipica elementelor de tip grinda (bare drepte încarcate cu forte normale pe axul lor). (fig.3.53). Fig.5.53. Intre momentul încovoietor si forta taietoare exista relatia stabilita anterior (partea a III-a) aceasta înseamna ca prezenta fortei taietoare atrage dupa sine variatia momentului încovoietor. Efectul momentului încovoietor (raspunsul barelor solicitate la încovoiere pura) a fost analizat în paragraful precedent. In paragraful de fata va fi analizat efectul fortei taietoare. 4.2. EFECTUL FORTEI TAIETOARE. FORFECAREA SI LUNECAREA Echilibrul tronsonului elementar din fig.3.54.a este asigurat, alaturi de fortele exterioare a-i revin, de eforturile sectionale M, T, M + dm, T + dT. Fig.3.54 Cele doua cupluri (M si M + dm) introduc în lungul fibrelor longitudinale compresiuni, respectiv întinderi, cu valori diferite în cele doua sectiuni (conf. schemei din fig. 3.54.b). Aceasta diferenta de valoare este sursa unei tendinte de lunecare de-a lungul oricarui plan longitudinal ce separa (imaginar) elementul de bara. Tendinta de lunecare este consecinta variatiei momentului încovoietor, deci a prezentei fortei taietoare în zona. (Pe zonele de bara cu forta taietoare nula, momentul încovoietor este constant si tendintele de lunecare sunt nule). Masura interactiunii dintre partea superioara si cea inferioara a elementului este perechea fortelor de lunecare dL; restabilind echilibrul fiecarei parti, fortele de lunecare blocheaza lunecarea si asigura integritatea formei. Pe un element de bara aflat deopotriva sub regimul fortelor taietoare si al fortelor de lunecare, interactiunea este masurata prin eforturi unitare tangentiale (fig.3.55). Conform principiului dualitatii eforturilor unitare tangentiale, eforturile unitare sunt egale si formeaza, împreuna cu cele de pe fetele opuse ale elementului , cupluri egale si de sens contrar (fig.3.56) Fig.3.55 Fig.3.56 4.3. REZISTENTA GRINZILOR IN PREZENTA FORTEI TAIETOARE 4.3.1. Eforturi unitare tangentiale. Formula lui Juravski Se considera volumul ABCD, decupat din bara (fig.3.57). Echilibrul de translatii pe directia axului barei (fig.3.58) este asigurat de fortele de interactiune a caror masura, pe sectiunea transversala este sistemul eforturilor unitare s, iar pe sectiunea longitudinala - forta elementelor de lunecare tbdz   (3.37) Fig.3.57 Fig.3.58 In prezenta unor momente încovoietoare pozitive, la partea superioara a barei, eforturile unitare t masoara compresiuni. Pe cele doua sectiuni transversale compresiunile sunt diferite, caci în prezenta fortei taietoare momentul încovoietor variaza. Cresterea de a rezultantei volumului de compresiuni este echilibrata de forta elementara de lunecare dL: dL = dC (3.38) Rezultanta volumului de compresiune cu expresia sdA unde A' este aria sectiunii transversale aflate în interactiune, înlocuind efortul s cu expresia (3.18), se obtine C = SA' , C = unde S'x este momentul static al suprafetei partiale A' a sectiunii transversale în raport cu axa x; de aici dC = dMx (3.39) Din (3.37), (3.38) si (3.39) rezulta bdz = dMx = si = (3.40) In expresia (3.40), care poarta numele lui Juravski, s reprezinta efortul unitar tangential yz din planul longitudinal egal cu efortul unitar tangential zy din planul sectiunii transversale; ambele planuri trec prin punctul C în care ne-am propus determinarea efectului fortei taietoare (fig.3.57 si 3.58). Semnificatia parametrilor din membrul drept al formulei lui Juravski este urmatoarea: T - forta taietoare din sectiune; S'x - momentul static în raport cu axa x (axa neutra a sectiunii) al suprafetei partiale A' determinate pe sectiunea transversala de planul longitudinal ce trece prin punctul C (punctul în dreptul caruia se defineste efortul tangential); momentul static al suprafetei A' este egal cu momentul static al suprafetei" (S'x + S"x = Sx = 0, caci Sx reprezinta momentul static al unei suprafete în raport cu o axa ce trece prin centrul de greutate; în valoare absoluta, S'x = S"x); b - latimea sectiunii transversale în dreptul punctului considerat; Ix - momentul de inertie al suprafetei sectiunii în raport cu axa x (axa neutra a sectiunii). Fig.3.58 4.3.2.1. Distributia eforturilor unitare pe sectiunea transversala; eforturi unitare tangentiale maxime. Asa cum rezulta din formula lui Juravski, parametrii care determina variatia eforturilor unitare . pe sectiunea transversala sunt b si S. La sectiunile dreptunghiulare (cu latime constanta), variatia eforturilor este determinata doar de variatia momentului static. Expresia momentului static, în functie de cota y a planului de lunecare, este (fig.3.59): S(y) = b ( Ei - si deci si efortului unitar - îi corespunde o variatie parabolica, simetrica în raport cu axa x, cu valori nule pentru y = h/2 (la extremitatile sectiunii) si valoarea Fig.3.59 maxima pentru y = 0 (în dreptul axei x, axa neutra a sectiunii). Pentru y = 0 Smax = tmax = tmax = 1,5 = 1,5 t med (3.41) unde s med s-a notat efortul unitar (fictiv) corespunzator unei distributii uniforme pe sectiunea transversala. La sectiunile de tip I si asimilate, cu sectiunea talpilor si a inimii de forma dreptunghiulara, distributia eforturilor unitare este cea din fig.3.60.a. Variatia parabolica este întrerupta de salturi în dreptul modificarii bruste a latimii sectiunii. Fig.3.60 Fig.3.61 In realitate aceasta variatie brusca a formei este sursa unor perturbatii în distributia teoretica a eforturilor unitare si generaeza concentraii de eforturi (fig.3.60.b). Pentru atenuarea vârfului de efort, sectiunile profilelor laminate de acest tip au laturile unite prin racordari (fig. 3.61). 4.3.2.2. Verificarea rezistentei la forfecare. La grinzi cu sectiune de forma dreptunghiulara eforturile unitare tangentiale sunt mici în comparatie cu eforturile unitare normale. Aplicatia din fig.3.ba este edificatoare. Fig.3.62 smax = tmax = 1,5 de unde Se vede ca pentru grinzi cu proportie normala, raportul tmax este net în favoarea efortului unitar t; de aceea aceste grinzi se verifica numai la încovoiere. In mod curent verificarea la forfecare nu este necesara nici în cazul grinzilor cu sectiune I sau asimilata acesteia, desi eforturile unitare tangentiale sunt mai mari ca cele corespunzatoare sectiunii dreptunghiulare. 4.3.3. Rezistenta barelor în sectiuni longitudinale (rezistenta la lunecare) 4.3.3.1. Determinarea fortei de lunecare. Variatia fortei de lunecare Observatie privind ipteza lui Bernoulli. Forta elementara de lunecare a fost determinata în paragraful 4.3.1. dL = dM Pe lungimea finita cuprinsa între doua sectiuni (A si B), unde AT este aria diagramei de forte taietoare cuprinsa între sectiunile A si B. La grinzile cu sectiune constanta (cazul curent), forta de lunecare este proportionala cu aria diagramei de forte taietoare, deci maxima spre reazemele grinzii. In planuri situate la cote diferite, forta de lunecare este proportionala cu momentul static, deci maxima în dreptul planului neutru. In fig.3.b se exprima aceasta variatii prin deplasari relative diferite între fâsii longitudinale de bara. Fig.3.63 Imaginea obtinuta infirma ipoteza lui Bernoulli (a sectiunilor plane..). Tipul de deformatie din fig.3.b3 este doar una din cele trei componente ale deformatii complexe cu care bara raspunde solicitarii de încovoiere cu forte taietoare; ele sunt prezentate în fig.3.64. Fig.3.64 4.3.3.2. Probleme practice privind asigurarea interactiunii longitudinale. Când dimensiunile prea mari ale sectiunii transversale nu permit realizarea grinzii dintr-o singura bucata, în planurile longitudinale care separa elementele componente ale grinzii se manifesta tendinte de lunecare (fig.3.65). In cele ce urmeaza se prezinta Fig.3.65 modul particular de blocare a acestor lunecari (asigurarea interactiunii longitudinale) la diferite tipuri de astfel de grinzi. I. Grinzi de lemn cu sectiune compusa La acest tip de grinda asigurarea interactiunii longitudinale se realizeaza, traditional, prin intermediul penelor (fig.3.66). Distanta dintre pene depinde de capacitatea lor la forfecare si de marimea de capacitatea lor la forfecare si de marimea fortelor de lunecare. La grinzile de mare deschidere sau în cazul în care forta taietoare prezinta variatii mari în lungul grinzii, se urmareste ca prin asezarea penelor la distante diferite (mici în zonele cu forta taietoare mare, deci lunecari puternice si mari zonele cu forta taietoare redusa) sa se realizeze o încarcare uniforma a penelor. fig.3.66 Istoria constructiilor si sistemul din fig.3.68, marcabil prin eleganta solutiei. fig.3.68 II. Grinzi metalice cu sectiune compusa de tip I sau asimilata. Asigurarea în turatiuni longitudinale între inima si talpi - elementele componente ale grinzii - se realizeaza prin îmbinari sudate (fig.3.69) sau nituite (3.70) fig.3.69 fig.3.70 III. Grinzi cu zabrele. Lunecarea dintre cele doua talpi este blocata de legaturi de tip pendul, asigurate de bare transversale simple, articulate la capete, compuse în sistem cu ochiuri triunghiulare (fig.3.71 si 3.72) Fig.3.71 Fig.3.72 Barele transversale (denumite, în functie de orientarea lor, diagonale sau montanti) sunt alternativ comprimate si întinse (pentru sensul tendintei de lunecare precizat în fig.3.71, diagonala din stânga este comprimata, iar cea din dreapta întinsa). IV. Grinzi Vierendel. Lunecarea dintre cele doua talpi este blocata de montanti robusti, încastrati la capete, formând, împreuna cu talpile, sisteme cu ochiuri dreptunghiulare (fig.3.73 si 3.74). Montantii sunt forfecati si încovoiati. V. Grinda de beton armat. Grinda de beton armat (fig.3.75 si 3.76) poate fi asimilata cu o grinda cu zabrele: talpa superioara (comprimata) este alcatuita din beton simplu (doar pe cca un sfert din înaltimea sa grinda de beton armat este comprimata), talpa inferioara (întinsa) este alcatuita din bare longitudinale de otel (armaturi) iar elementele transversale "de coasere" ale celor doua talpi - din "vine" de beton comprimat si armaturi întinse (în doua variante: bare înclinate, de tip diagonale si etrieri, de tip montanti). 5.1. DEFINITIA SOLICITARII. EXEMPLE Compresiunea (întinderea) excentrica este o solicitare compusa, în prezenta careia, pe sectiunea transversala, interactiunea este reprezentata de o forta axiala si un moment încovoietor (vector cuplu cuprins în planul sectiunii). In functie de directia vectorului moment încovoietor fata de axele principale de inertie ale sectiunii transversale, se deosebesc urmatoarele doua cazuri: - încovoiere oblica cu forta axiala (cazul general de compresiune sau întindere excentrica), când directia vectorului cuplu este oarecare fata de directia axelor; - încovoiere simpla cu forta axiala (cazul particular), când directia vectorului cuplu coincide cu directia uneia din axe. O pereche de forte echilibrate aplicate pe o bara dreapta de-a lungul unui suport paralel cu axa barei genereaza, între punctul de aplicatie, compresiune (întindere) excentrica (fig.3.77). In aria sectiuni transversala, masura interactiunii este o forta normala A = P, aplicata excentrica, de-a lungul suportului. fortelor exterioare, ea se reduce în centrul de greutate al sectiunii la o forta axiala N = P si un cuplu M = Pl, unde e este excentricitatea punctului de aplicatie a fortei interioare. Când punctul de aplicatie se afla pe una din axele principale de inertie (fig.3.78) se genereaza cazul particular de compresiune excentrica - încovoierea simpla cu forta axiala. fig.3.78 In practica, compresiunea excentrica este solicitarea caracteristica a stâlpilor de cadru în regim gravitantional de solicitare (fig.3.79). Fig.3.79 5.2. INCOVOIEREA SIMPLA CU FORTE AXIALE 5.2.1. Eforturi unitare pe sectiunea transversala Determinarea eforturilor unitare pe sectiunea transversala se face prin suprapunerea efectelor celor doua solicitari (simple) componente: compresiunea (întinderea) centrica si încovoierea .. Ambele genereaza pe sectiunea transversala eforturi unitare normale t (fig.3.80). Fig.3.80 Intr-un punct curent al sectiunii, efortul unitar corespunzator solicitarii compuse se obtine prin însumarea eforturilor unitare corespunzatoare fiecarei solicitari simple. t tN tM La distanta y de axa x , cu semnele corespunzatoare sensului eforturilor unitare t = 5.2.2. Semnele eforturilor si conditiile de încarcare Eforturile unitare însumate pot avea acelasi semn (când domina efectul fortei axiale) sau semne diferite (când domina efectul momentului încovoietor). Daca elementele supuse la compresiune excentrica (stâlpi, arce etc) sunt alcatuite din materiale nerezistente la întindere (piatra, caramida, etc.) se urmareste ca sectiunea sa fie comprimata în totalitatea ei. Pentru aceasta este necesar ca (în valoare absoluta) ......, unde ..... reprezinta efortul maxim de întindere corespunzator momentului încovoietor: de unde l = (3.43) La o sectiune dreptunghiulara, indiferent de proportiile ei, (3.44) Pentru excentricitati inferioare valorii h/b adica pentru pozitii ale fortei de compresiune cuprinse în treimea mijlocie a sectiunii dreptunghiulare, eforturile vor avea acelasi semn (compresiuni). Tipurile de diagrama, în corespondenta cu pozitia fortei fata de treimea mijlocie, sunt prezentate în fig.3.87. Fig.3.81 5.3. INCOVOIERE OBLICA CU FORTA AXIALA 5.3.1. Descompunerea solicitarii compuse in solicitari simple Forta P aplicata în punctul P (xo,y) se reduce în centrul de greutate al sectiunii la o forta axiala N = P si doua momente încovoietoare: Mx Pyo si My = Pxo. Reducerea s-a facut în doua etape. din punctul P în punctul P1 si din P1 în centrul de greutate; etapele sunt prezentate în fig.3.82. fig.3.82 Cele trei eforturi sectionale (N, Mx, My) le corespund eforturi unitare normale . Intr-un punct curent al sectiunii, efortul unitar corespunzator solicitarii compusa se obtine prin însumarea eforturilor unitare corespunzatoare fiecarei solicitari simple: t tn tMx tmy In punctul M (x,y), t = + , t = - , t = - , (3.45) 5.3.2. Axa neutra 5.3.2.1. Ecuatia axei neutre. Axa neutra este locul geometric al punctelor cu eforturi unitare nule. Din conditia t = 0 rezulta ecuatia axei: 1 + = 0 = 1 sau, cu notatiile - = a si - = b (3.46) = 1 (3.48) Axa neutra este o dreapta care taie axele de referinta la distantele a si b de originea aflata în centrul de greutate al sectiunii (fig.3.83) fig.3.83 5.3.2.2. Proprietatile axei neutre. A. Intrucât, conform relatiilor (3.46), la valori pozitive ale coordonatelor xo, yo corespund valori negative ale distantelor a si b, fata de punctul de aplicatie a fortei, axa neutra se afla de cealalta parte a centrului de greutate (fig.3.84). B. Punctelor de aplicatie a fortei aflate pe o dreapta ce trece prin centrul de greutate le corespund axe neutre parafele, caci = const. Conform relatiilor (3.46) , axa neutra se apropie de centrul de greutate când punctul de aplicatie se departeaza (fig.3.85). fig.3.84 fig.3.85 C. Punctelor de aplicatie ale fortei aflate pe o dreapta care nu trece prin centrul de greutate le corespund axe neutre concurente (fara demonstratie) (fig.3.86). fig.3.86 5.3.4.3. Sîmburele central al unei sectiuni dreptungiulare. Fie sectiunea dreptunghiulara din fig. 3.88, cu dimensiunile laturilor B si H. fig.3.87 conform (3.46) xo = - , yo = - Pozitiei (1) a axei neutru, tangenta la una din laturile mici ale sectiunii (cu a a si b = - H/2), îi corespunde punctul 1 de aplicatie a fortei, cu coordonatele. xo = 0 yo = - Pozitiei (2) a axei neutre, tangenta la una din laturile mari ale sectiunii, îi corespunde punctul 2 cu coordonatele xo = y = o Când axa neutra se roteste în jurul punctului A, punctul de aplicatie a fortei parcurge segmentul 1-2. Prin anologie, se deduce Fig.3.88 Fig.3.89. si pozitia punctelor simetrice 3 si 4 si segmentele 2-3, 3-4 si 4-1 care închid sâmburile central. Acesta este un romb cu diagonalele egale cu o treime din lungimea laturilor dreptunghiului (fig.3.89). 5.3.4.4. Sâmburele central al unei sectiuni circulare este un cerc cu diametrul egal cu un sfert din diametrul sectiunii (fig. 3.90 si 3.91): yo = Fig.3.90 Fig.3.91 5.4. Eforturi unitare pe talpa unei fundatii Pamântul este un material nerezistent la întindere. De aceea, la contractul dintre fundatie si teren, interactiunea nu poate fi realizata decât prin eforturi de compresiune. Daca forta este aplicata în interiorul sâmburelui central, distributia presiunilor se face pe toata suprafata talpii, dupa legea trapezoidala precizata anterior (fig.3.92). Daca forta este aplicata în afara sâmburelui central, distributia presiunilor se face pe o zona limitata a suprafetei talpii, numita zona activa (fig.3.93). Fig.3.92 Fig.3.93 Suprafata zonei active si valoarea efortului unitar maxim se determina din conditia ca forta P, aplicata exentric si rezultanta R a volumului de presiuni sa formeze un sistem echilibrat. Daca P calca pe una din axele de simetrie ale unei fundatii dreptunghiulare, la distanta C de marginea fundatiei (fig. 3.93), latimea zonei active este d = 3 c, iar efortul unitar maxim, de doua ori mai mare decât efortul mediu smax = 2 Document Info Accesari: 30328 Apreciat: Comenteaza documentul: Nu esti inregistrat Trebuie sa fii utilizator inregistrat pentru a putea comenta Creaza cont nou A fost util? Daca documentul a fost util si crezi ca merita sa adaugi un link catre el la tine in site Copiaza codul: in pagina web a site-ului tau. <a href="https://www.scritub.com/tehnica-mecanica/REZISTENTA-SI-RIGIDITATEA-ELEM337727.php" target="_blank" title="REZISTENTA SI RIGIDITATEA - ELEMENTELOR DE TIP BARA - https://www.scritub.com">REZISTENTA SI RIGIDITATEA - ELEMENTELOR DE TIP BARA</a> eCoduri.com - coduri postale, contabile, CAEN sau bancare Politica de confidentialitate | Termenii si conditii de utilizare Copyright © Contact (SCRIGROUP Int. 2024 )