SEMNALE ALEATOARE
3.1 Definitia si clasificarea semnalelor aleatoare:
Semnalele care apar in natura si in tehnica se impart in trei mari clase:
Dupa tipul discret sau continuu al domeniului amplitudinilor si multimii de timp T, semnalele aleatoare se impart in 4 categorii mai importante pe care le-am reprezentat in fig.3.2 printr-o singura realizare x(wk, t) = x(k)(t).
Procesul aleator continuu: semnalul aleator are atat domeniul amplitudinilor X cat si domeniul de timp continuu.
xk(t)
![]()
t
x1
x2
a) in sens larg
b) in sens strict
3.2 Variabile aleatoare
Expresia cantitativa a realizarilor unui eveniment aleator poarta numele de variabila aleatoare. Variabilele aleatoare pot fi continue sau discrete dupa cum valorile numerice pe care le pot lua apartin unui interval sau unei multimi numarabile de valori.
Ex.2:
F1(x3) = P = P1+P2+P3 = 0,75; avem in plus F1(x<x1) = 0 si F1(x>x5) = 1
Ex.3: sau
n
0.85 F1(x)=å Pk u(x-xk); Pk=P
0.75 k=1
³
si u (x) =
0 ; x<
fig.1.3
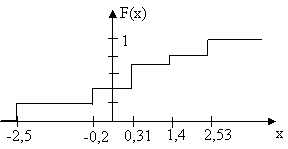
In cazul unei v.a. continue functia de repartitie arata ca in figura urmatoare:
P= F(x2)-F(x1)
Dem. F(x2)=P= P= P+ P=
==>P= F(x2)-F(x1) .
fig. 1.4
3.2.2 Densitatea de probabilitate a unei v.a.
Daca functia de repartitie a unei v.a. continue este continua si derivabila, derivata sa se numeste densitate de probabilitate:
![]()
![]()
Din probabilitatea ca o variabila aleatoare sa ia valori cuprinse intr-un interval (x1,x2) se poate deduce acum definitia densitatii de probabilitate:
x2
P= ò p1(x) dx
x1
Pentru cazul unor v.a. discrete
n
F1(x) = ∑ Pj u(x-xj); unde Pj=P
³
iar u(x)=
0 ; x<0
este functia treapta unitara; ca urmare functia
densitate de probabilitate va fi:
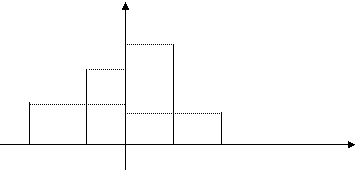
P3
P2 Fig.3.5
P1
P4
x1 x2 x3 x4 . . . . x
Fig. 3.6
F1(x)
P1(x) = = å Pj d(x-xj) si arata ca in fig .3.6 prezentata mai sus.
x j
In continuare prezentam doua din cele mai intalnite distributii de v.a. precum si cateva din proprietatile acestora.
3.2.3 Distributia uniforma
In acest caz functia de repartitie si densitatea de probabilitate de ordinul intai sunt:
![]()
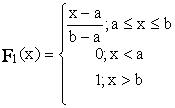
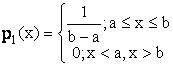
F1(x) P1(x)
b - a
a b x a b x
3.2.4 Distributia normala
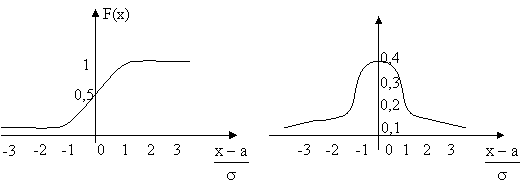
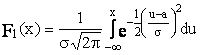
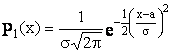
a = valoarea medie a v.a. s = dispersia v.a
sau normalizand: ![]()
![]() ;
; ![]()
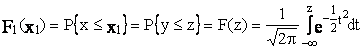
F(z) poarta numele de integrala Laplace si se gaseste in tabele.
3.2.5 Momentele de ordinul k ale v.a.
Functia de repartitie si densitatea de probabilitate a v.a. dau o caracterizare completa a v.a., dar in multe aplicatii sunt necesari doar niste parametrii pentru caracterizarea v.a.. Acesti parametrii sunt de obicei momentele de ordinul k.
¥
mk( x ò xk p1(x) dx pt. v.a. continua
-¥
n
mk( x å xkI pi unde pi=P
i=1
Cunoasterea tuturor momentelor de ordin k inseamna de obicei cunoasterea completa a v.a.. In practica se utilizeaza doar trei:
Valoarea medie de ordinul 1
¥
a = m1 = ò x p1(x) dx v.a. continua
-¥
n
å xi Pi v.a. discreta
i=1
Media de ordinul 2
Dispersia (sau varianta) v.a , s
3.3 Valori medii ale semnalelor aleatore
3.3.2 Valori medii temporale ale semnalelor aleatoare
In acest caz din multimea realizarilor wIW se considera o realizare particulara x(t, wk)=x(k)(t) si se calculeaza valorile medii temporale ale acesteia.
![]() care nu depinde de originea timpului t0 si reprezinta puterea
medie a semnalului pe o sarcina unitara.
care nu depinde de originea timpului t0 si reprezinta puterea
medie a semnalului pe o sarcina unitara.
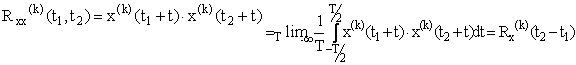
- functia de autocorelatie
temporala:
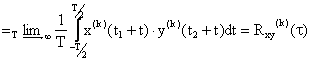
aceasta nu depinde de originea timpului si numai de t=t2-t1
![]()
- functia de corelatie
mutuala temporala:
acesta nu depinde de originea timpului. In general, Rxy (k)(t) nu este o functie simetrica.
Cu ajutorul definitiilor proprietatilor statistice ale semnalelor aleatoare putem caracteriza principalele clase de semnale aleatoare prezentate. O clasa de semnale aleatoare cu o deosebita importanta practica sunt semnalele aleatoare stationare. Acestea sunt acele semnale aleatoare ale caror proprietati statistice sunt invariante la schimbarea arbitrara a originii timpului.
Pn(x1,x2,.,xn,t1,.,tn)=pn(x1,.,xn,t1+t,.,tn+t
Semnalele care se bucura de proprietatea anuntata se numesc semnale aleatoare in sens STRICT.
Semnalele aleatoare 252g62c ergodice sunt semnale stationare in sens strict care au proprietatea ca mediile statistice sunt egale cu cele temporale. Adica :
![]()
![]()
![]()
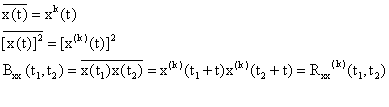
functiile de autocorelatie
Clasa semnalelor ergodice are o deosebita insemnatate deoarece elimina necesitatea obtinerii tuturor realizarilor unui semnal aleator x(t), putandu-se determina probabilitatile statistice dintr-o singura realizare.
Semnalul aleator pur este acel semnal pentru care variabilele aleatoare succesive ale lui x(t) luate la intervale oricat de mici sunt independente. Se poate exprima acest fapt prin:
Se observa ca acest semnal este descris complet de densitatea de probabilitate de ordinul intai. Zgomotul alb este un semnal aleator pur si are functia de autocorelatie egala cu functia Dirac.
Deoarece asa cum vom vedea densitatea spectrala de putere a semnalului aleator este pereche Fourier cu functia de autocorelatie, rezulta ca zgomotul alb are un spectru de putere uniform si infinit.
3.4 Densitatea spectrala de putere. Teorema Wiener - Hincin
3.4.1 Densitatea spectrala de putere a semnalelor aleatoare stationare
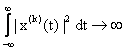
Si ca atare nu se poate aplica analiza armonica a semnalelor deterministe. Pentru a se putea extinde analiza spectrala si in cazul semnalelor aleatoare se considera semnalul xT(k)(t) dintr-o realizare particulara x(k)(t) a semnalului aleator x(t).
Puterea medie a semnalului trunchiat este:
![]()
Daca se noteaza cu:
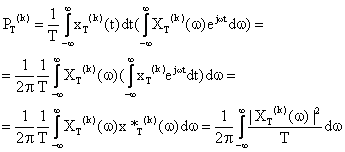
rezulta :
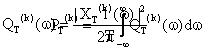
Densitatea spectrala de putere a semnalului trunchiat se defineste
prin relatia:
![]()
iar puterea medie a realizarii xT(k)(t) este:
![]()
Deoarece | xT(k)(w)|2 este o functie para de w, densitatea spectrala de putere poate fi definita in domeniul w>0 prin:
![]()
In cazul in care se considera ca intreaga realizare T tinde la infinit, rezulta puterea medie a semnalului, presupunand existenta limitei:
Aceasta presupunere este justificata deoarece semnalul are intotdeauna o putere finita. Deoarece nu ne intereseaza puterea unei realizari particulare (k), ci puterea medie a semnalului aleator inainte de a trece de la limita in relatia de mai sus se face o mediere peste toate realizarile si obtinem puterea medie:
![]()
este densitatea spectrala de putere DSP.
DSP se poate definii si pentru frecventele ne negative:
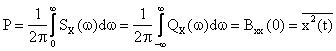
![]() U(w)=1 , daca w>=0
U(w)=1 , daca w>=0
U(w)=0 , daca w<0
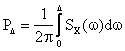
Puterea unui semnal aleator intr-o banda D finita se obtine din:
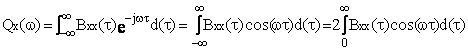 Teorema Wiener -
Hincin, reprezinta un rezultat remarcabil al teoriei semnalelor aleatoare
stationare si afirma ca densitatea spectrala de putere si functia de
autocorelatie ale unui semnal aleator sunt perechi Fourier. Adica
Teorema Wiener -
Hincin, reprezinta un rezultat remarcabil al teoriei semnalelor aleatoare
stationare si afirma ca densitatea spectrala de putere si functia de
autocorelatie ale unui semnal aleator sunt perechi Fourier. Adica
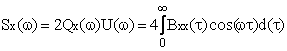
![]()
si reciproc.
![]()
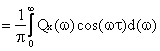
![]()
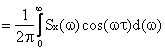
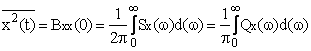 Puterea totala a unui semnal aleator este:
Puterea totala a unui semnal aleator este:
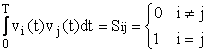
Dorim sa reprezentam semnalul aleator x(t) in forma
![]()
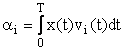
Aceasta integrala este o integrala de tip medie patratica si reprezinta o v.a.
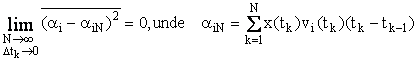
Iar limita se defineste in sensul mediei patratice
![]()
Trebuie sa alegem in asa fel functiile de baza astfel incat coeficientii dezvoltarii ai sa fie necorelati. Astfel daca presupunem ca media semnalului x(t) este nula, adica
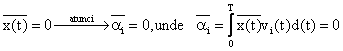
Stabilim acum ca daca functiile vi (t) sunt solutii ale ecuatiei integrale
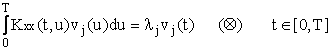
Unde Kxx (t,u) este functia de covariatie a semnalului aleator x(t), atunci coeficientii ai sunt necorelati si indeplinesc conditia
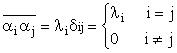
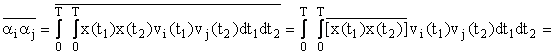
care este finita si neuniforma, forma sa fiind dictta de functia de transfer H(w) a sistemului liniar. Alta deosebire consta in faptul ca functia sa de autocorelatie nu mai este o functie Dirac.
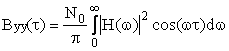
iar puterea totala are expresia
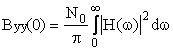
|