Studiul circuitului r, l, c in curent alternativ. imbunatatirea factorului de putere.

STUDIUL CIRCUITULUI R, L, C IN CURENT ALTERNATIV. IMBUNATATIREA FACTORULUI DE PUTERE

SCOPUL LUCRARII

Lucrarea are ca scop studiul unui circuit RLC serie si a rezonantei de tensiuni, al unui circuit RLC paralel si a rezonantei de curent, precum si imbunatatirea factorului de putere in curent alternativ monofazat.

2.CONSIDERATII TEORETICE

2.1. Studiul circuitului RLC serie in curent alternativ si a rezonantei de tensiuni

Se considera un circuit serie, format dintr-un rezistor ideal cu rezistenta R, o bobina ideala cu inductivitate L si un condensator ideal cu capacitatea C, alimentat cu tensiunea sinusoidala (figura 4.1):

Tensiunea pe bobina este data de relatia : 636c25g

(4.7)

sau in complex:

(4.8)

Complexul curentului se deduce din ecuatia (4.4):

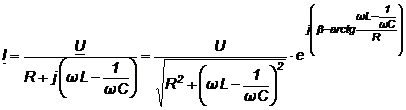(4.9)

Considerand reactantele inductiva si capacitiva:

(4.10)

reactanta circuitului va fi : (4.11)

daca defazajul j este nul ( fig. 4.2.b), deci circuitul are caracter rezistiv;

daca , defazajul j este pozitiv (fig. 4.2.c), deci circuitul are caracter inductiv.

In circuitele electrice care contin bobine si condensatoare, pot exista cazuri cand reactanta echivalenta a intregului circuit este nula (X=0), intrucat reactantele inductive si capacitive se compenseaza reciproc. In aceste cazuri, unghiul de defazaj j dintre tensiunea aplicata la borne si curentul care se stabileste in circuit este nul (j =0), de asemenea puterea reactiva consumata de circuit este nula (Q=UIsinj=XI =0). Aceste regimuri de functionare ale circuitului se numesc regimuri de rezonanta.

Asadar, pentru circuitul din figura 4.1, regimul este rezonant daca :

(4.16)

Analizand aceasta relatie se constata ca rezonanta poate fi realizata fie prin variatia frecventei (f= w p), fie prin variatia parametrilor (inductivitatea bobinei sau capacitatea condensatorului).

Rezonanta intr-un circuit R, L, C serie se mai numeste si rezonanta de tensiune, deoarece la rezonanta caderea de tensiune inductiva si capacitiva se compenseaza una pe alta (valorile lor efective putand fi mai mari decat valoarea efectiva a tensiunii aplicate U):

(4.17)

asa cum s-a reprezentat in figura 4.2.b.

La rezonanta, impedanta circuitului are valoarea minima (Z=R), iar valoarea efectiva a curentului atinge valoarea maxima :

(4.18)

2.2. Studiul circuitului RLC paralel in curent alternativ si al rezonantei de curenti

In figura 4.3 se reprezinta un circuit, format prin legarea in paralel a unui rezistor ideal cu rezistenta R, a unei bobine ideale cu inductivitatea L si a unui condensator ideal cu capacitatea C, alimentat cu tensiunea sinusoidala:

Figura 4.3

a.   b. c.

Figura 4.4

si valorile lor efective pot fi mai mari decat valoarea efectiva I a curentului i. Curentul I la rezonanta are valoarea minima data de relatia:

(4.27)

deoarece admitanta circuitului este minima:

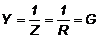(4.28)

a. b. c.

Figura 4.5

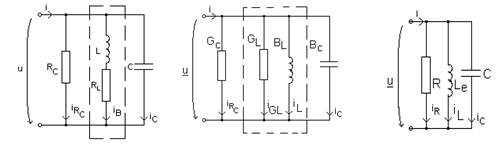
Se inlocuiesc cele doua conductante in paralel cu o conductanta echivalenta: (4.33)

respectiv cu o rezistenta echivalenta:

(4.34)

si susceptanta BL printr-o bobina echivalenta, adica cu reactanta Xe wLe, data de relatia:

(4.35)

respectiv cu o inductivitate:

(4.36)

a. b. c.

Figura 4.6

2.3. Imbunatatirea factorului de putere intr-un circuit alternativ monofazat

Figura 4.7

Figura 4.8

Puterea absobita de receptor inainte de compensare este:

(4.51)

Curentul absorbit de condensatorul C este :

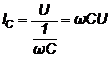(4.52)

fiind defazat cu p/2 inaintea tensiunii aplicate, astfel incat sursa furnizeaza curentul total dat de ecuatia in complex :

Figura 4.9

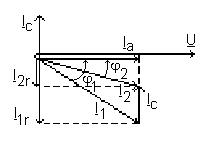
Din diagrama fazoriala (figura 4.9) rezulta:

(4.53)

sau

(4.54)

Fig.4.11 Montajul experimental pentru determinarea rezistentei R_L a bobinei

Figura 4.12 Montajul experimental pentru studiul circuitului RLC paralel in c.a. si a rezonantei de curenti

unde: K – intrerupator bipolar;

Figura 4.13 Montajul experimental pentru imbunatatirea factorului de putere

unde:

K,K₁ – intrerupatoare bipolare;

cosj – cosfimetru 5A, 220V;

A₁, A₂, A₃ – ampermetre de curent alternativ, 2A;

V – voltmetru de curent alternativ, 300V;

M – motor electric monofazat, cosj

C(C^’, C^”) – condensator 300V, montat in derivatie

4. DESFASURAREA LUCRARII

4.1. Studiul circuitului RLC serie in curent alternativ si a rezonantei de tensiuni

Se realizeaza montajul din figura 4.10. Se pune autotransformatorul ATR pe pozitia de tensiune nula si reostatul R_C pe valoarea medie a rezistentei. Se inchide intrerupatorul K.

Se regleaza cu ajutorul autotransformatorului ATR o tensiune U=50V, indicata de voltmetrul V.

Tabelul 4.1

Se determina rezistenta RL a bobinei (echivalenta pierderilor in fier si rezistentei infasurarii bobinei). In acest scop se realizeaza montajul din figura 4.11. Semnificatia aparaturii utilizate este aceeasi ca in figura 4.10. Se va efectua o masuratoare pentru o pozitie a bobinei cu inductanta variabila corespunzatoare rezonantei stabilindu-se prin bobina curentul mediu obtinut in timpul masuratorilor pentru obtinerea rezonantei. Rezistenta bobinei determinata in c.a. este:

si valoarea sa se trece in tabelul 4.2.

Tabelul 4.2

Pe baza masuratorilor efectuate la punctul 4.1.1 se vor ridica experimental curbele de variatie a curentului I, a caderii de tensiune pe bobina UB , a caderii de tensiune pur inductive UL, a caderii de tensiune pe condensator UC, a factorului de putere a circuitului cos j, obtinute prin variatia inductivitatii bobinei, in functie de reactanta bobinei XL, care au alura din figura 4.14.

Figura 4.14

Rezistenta reostatului este:

iar rezistenta echivalenta a circuitului este:

Caderea de tensiune pur inductiva este:

La rezonanta:

Factorul de putere al circuitului este:

Factorul de putere al circuitului este maxim la rezonanta.

Marimile calculate se trec in tabelul 4.3

Tabelul 4.3

Se executa montajul din figura 4.11. Se alimenteaza montajul cu tensiune de la versatester si se modifica frecventa pana la obtinerea rezonantei. Parametrii circuitului nu se modifica. Se citeste indicatia aparatelor de masura, iar rezultatele se trec in tabelul 4.4.

Tabelul 4.4

4.2. Studiul circuitului RLC paralel in curent alternativ si al rezonantei de curenti

Se realizeaza montajul din figura 4.12. Se pune autotransformatorul ATR pe pozitia de tensiune nula si reostatul R_C pe valoarea maxima a rezistentei. Se inchide intrerupatorul K.

Se regleaza cu ajutorul autotransformatorului ATR o tensiune U=50V, indicata pe voltmetrul V.

valori care se trec in tabelul 4.6.

Tabelul 4.6

Pe baza masuratorilor efectuate la punctul 4.2.1 se vor ridica experimental curbele de variatie a curentului I, a curentului prin bobina IB, a componentei reactive IL a curentului prin bobina , a curentului prin condensator IC, a factorului de putere a circuitului cos j, obtinute prin variatia inductivitatii bobinei, in functie de reactanta bobinei XL, care au alura din figura 4.15.

Figura 4.15.

Se vor calcula parametrii circuitului si se vor construi grafic diagramele fazoriale ale tensiunilor pentru trei puncte de functionare: inainte, dupa si la rezonanta (vezi figura 4.4).

Conductanta reostatului este:

Conductanta echivalenta a circuitului este:

Impedanta bobinei (ZL), reactanta sa (XL), susceptanta inductiva (BL), si inductanta (L), se calculeaza cu relatiile:

Componenta reactiva a curentului prin bobina se determina cu relatia:

Susceptanta (Bc) si capacitatea (C) a condensatorului se determina cu relatiile:

Susceptanta echivalenta (B) si admitanta echivalenta(Y) a circuitului se determina cu relatiile:

Tabelul 4.7

4.2.5. Se executa montajul din figura 4.12. Se alimenteaza montajul cu tensiune de la versatester si se modifica frecventa pana la obtinerea rezonantei. Parametrii circuitului nu se modifica. Se citeste indicatia aparatelor de masura, iar rezultatele se trec in tabelul 4.8.

Tabelul 4.8

4.3. Imbunatatirea factorului de putere intr-un circuit alternativ monofazat

Se efectueaza montajul din figura 4.13, K fiind deschis, se inchide K. Se citesc U, I , cosj

Tabelul 4.9

5. Continutul referatului

Se vor completa tabelele de mai sus si se vor face observatii si interpretari asupra rezultatelor masuratorilor.

Se va raspunde la urmatoarele intrebari :

1. Ce se intelege prin rezonanta de tensiune?

2. In ce conditii are loc rezonanta de tensiune pentru un circuit RLC serie?

3. Ce se intelege prin rezonanta de curenti?

4. In ce conditii are loc rezonanta de curenti pentru un circuit RLC paralel?

5. Ce metode se folosesc pentru imbunatatirea factorului de putere?

6. De ce este necesara imbunatatirea factorului de putere?