Vom
considera un punct material care executa oscilatii īn jurul unei
pozitii de echilibru, de-a lungul unei axe pe care o vom lua drept
axa ![]() . Se constata ca sistemul are un singur grad de
libertate si vom nota cu
. Se constata ca sistemul are un singur grad de
libertate si vom nota cu ![]() abscisa punctului de
echilibru. Fie
abscisa punctului de
echilibru. Fie ![]() energia
potentiala a sistemului, cu conditia
energia
potentiala a sistemului, cu conditia ![]() minim. Īn vecinatatea punctului de echilibru
functia
minim. Īn vecinatatea punctului de echilibru
functia ![]() se poate dezvolta īn
serie Taylor:
se poate dezvolta īn
serie Taylor:
|
|
(II.84) |
Notānd ![]() abaterea de la
pozitia de echilibru, relatia (II.84) devine:
abaterea de la
pozitia de echilibru, relatia (II.84) devine:
|
|
(II.85) |
Īn expresia (II.85) se pot face urmatoarele simplificari:
- īntrucāt energia potentiala
este definita pāna la o constanta aditiva arbitrara,
pute 727e46h m considera ![]() ;
;
- īn pozitia de echilibru ![]() fiind minima,
fiind minima, ![]() .
.
Notānd
|
|
(II.86) |
expresia (II.85) devine:
|
|
(II.87) |
Īn cazul
oscilatiilor armonice termenii de gradul ![]() sunt nuli; daca
acesti termeni nu sunt nuli, oscilatiile sunt anarmonice.
sunt nuli; daca
acesti termeni nu sunt nuli, oscilatiile sunt anarmonice.
Energia
cinetica a particulei va fi ![]() , deci functia Lagrange se scrie:
, deci functia Lagrange se scrie:
|
|
(II.88) |
Ecuatia
Lagrange ![]() devine:
devine:
|
|
(II.89) |
care este o ecuatie diferentiala de ordinul al doilea.
Īn cazul oscilatiilor armonice ecuatia de miscare va fi:
|
|
(II.90) |
care are solutia:
|
|
(II.91) |
sau notānd ![]()
|
|
(II.92) |
O alta forma pentru solutia ecuatiei (II.90) este:
![]()
unde constantele de integrare
sunt ![]() si
si ![]() .
.
Oricare ar
fi forma solutiei, cele doua constante care apar se determina
din conditiile la momentul initial. Daca, de exemplu, la
momentul initial particula era īn pozitia de echilibru ![]() si avea viteza
si avea viteza ![]() , obtinem pentru cele doua constante sistemul de
ecuatii:
, obtinem pentru cele doua constante sistemul de
ecuatii:
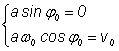
din care ![]() iar
iar ![]() , deci solutia va fi:
, deci solutia va fi:
|
|
(II.93) |
Rezolvānd
aceeasi problema īn formalismul Hamilton, functia ![]() va fi:
va fi:
![]()
care īnsa trebuie
exprimata īn functie de ![]() si
si ![]() . Din expresia (II.88):
. Din expresia (II.88):
![]() , de unde
, de unde ![]() iar
iar
|
|
(II.94) |
Sistemul ecuatiilor canonice:
![]()
devine
|
|
(II.95) |
din care se elimina ![]() si se obtine
si se obtine
![]()
adica aceeasi ecuatie (II.90) ca si īn cazul formalismului Lagrange.
Pentru
oscilatorul armonic unidimensional spatiul fazelor este bidimensional
si are "axele" ![]() si
si ![]() .
.
Sa determinam ecuatia traiectoriei punctului reprezentativ al sistemului īn spatiul fazelor. Pentru aceasta scriem energia oscilatorului:
|
|
(II.96) |
care este o integrala prima a miscarii, deci este constanta. Relatia (II.96) se mai poate scrie:
|
|
(II.97) |
care este ecuatia unei
elipse cu semiaxele ![]() si
si ![]() .
.
Fie un
sistem conservativ cu ![]() grade de libertate, a
carui configuratie este descrisa de coordonatele generalizate
grade de libertate, a
carui configuratie este descrisa de coordonatele generalizate ![]() avānd la echilibru
valorile
avānd la echilibru
valorile ![]() . Īn cazul micilor oscilatii īn jurul pozitiei de
echilibru si tinānd seama ca
. Īn cazul micilor oscilatii īn jurul pozitiei de
echilibru si tinānd seama ca 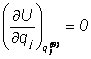 , expresia energiei potentiale se scrie:
, expresia energiei potentiale se scrie:
|
|
(II.98) |
Admitānd ca īn starea de echilibru energia potentiala este nula si notānd:

relatia (II.98) devine:
|
|
(II.99) |
care este o functie patratica omogena de coordonatele generalizate.
Vom arata ca si energia cinetica a unui sistem conservativ se poate scrie sub o forma asemanatoare:
fie
![]() coordonatele
carteziene ale punctelor sistemului, exprimate īn functie de coordonatele
generalizate
coordonatele
carteziene ale punctelor sistemului, exprimate īn functie de coordonatele
generalizate ![]() prin relatiile:
prin relatiile:
![]()
- vitezele carteziene:
![]()
energia cinetica:
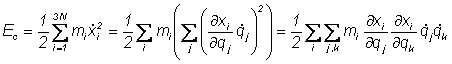
|
|
(II.100) |
unde am notat ![]()
Din relatiile (II.99) si (II.100), functia Lagrange se scrie:
|
|
(II.101) |
Ecuatiile Lagrange vor fi:
|
|
|
(II.102) |
care constituie un sistem
de ![]() ecuatii
diferentiale liniare de ordinul al doilea, cu coeficienti
constanti. Solutiile acestor ecuatii vor fi de forma:
ecuatii
diferentiale liniare de ordinul al doilea, cu coeficienti
constanti. Solutiile acestor ecuatii vor fi de forma:
|
|
(II.103) |
care substituite īn
(II.102) duc la un sistem omogen de ecuatii algebrice pentru constantele ![]() de forma:
de forma:
|
|
|
(II.104) |
Acesta admite solutie nebanala cānd determinantul coeficientilor este nul, adica:
|
|
(II.105) |
cu mentiunea (evidenta din definitii) ca:
![]()
Expresia
(II.105) reprezinta o ecuatie algebrica de gradul ![]() īn
īn ![]() , denumita ecuatie
seculara; ea admite
, denumita ecuatie
seculara; ea admite ![]() radacini
reale
radacini
reale ![]() .
.
O valoare ![]() , radacina reala a acestei ecuatii,
se numeste pulsatie proprie a
sistemului.
, radacina reala a acestei ecuatii,
se numeste pulsatie proprie a
sistemului.
Constantele
![]() din (II.104) vor fi
functii de aceste pulsatii proprii iar solutia generala a
sistemului (II.102) va fi o combinatie liniara de solutii
particulare (II.103):
din (II.104) vor fi
functii de aceste pulsatii proprii iar solutia generala a
sistemului (II.102) va fi o combinatie liniara de solutii
particulare (II.103):
![]()
Partea ei reala se exprima astfel:
|
|
(II.106) |
unde ![]() sunt constante.
sunt constante.
Solutia
(II.106) este o suprapunere de ![]() oscilatii cu
pulsatiile
oscilatii cu
pulsatiile ![]() , amplitudinile
, amplitudinile ![]() si fazele
initiale
si fazele
initiale ![]() . O expresie de tipul:
. O expresie de tipul:
|
|
(II.107) |
se numeste coordonata normala ![]() si solutia
generala (II.106) devine:
si solutia
generala (II.106) devine:
|
|
|
(II.108) |
Cu
ajutorul coordonatelor normale ![]() functia Lagrange
se poate scrie:
functia Lagrange
se poate scrie:
|
|
(II.109) |
unde ![]() si
si ![]() sunt constante reale.
sunt constante reale.
Facānd
schimbarea de variabila ![]() si
si 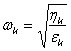 , expresia (II.109) devine:
, expresia (II.109) devine:
|
|
(II.110) |
Ecuatiile Lagrange vor fi:
|
|
|
(II.111) |
care reprezinta ![]() oscilatori independenti.
oscilatori independenti.
Īn concluzie,
micile oscilatii ale unui sistem cu ![]() grade de libertate
sunt echivalente cu micile oscilatii ale unui sistem de
grade de libertate
sunt echivalente cu micile oscilatii ale unui sistem de ![]() oscilatori
independenti, cu conditia ca acestia sa execute oscilatii normale.
oscilatori
independenti, cu conditia ca acestia sa execute oscilatii normale.
Consideram
un sistem format din doua corpuri cu masele ![]() si
si ![]() , ale caror pozitii sunt date de vectorii de
pozitie
, ale caror pozitii sunt date de vectorii de
pozitie ![]() si
si ![]() (fig.II.4)
(fig.II.4)
|
Fig.II.4 |
Presupunem
ca cele doua corpuri interactioneaza cu forte
conservative care provin din potentialul ![]() . Atunci functia Lagrange a sistemului se va scrie:
. Atunci functia Lagrange a sistemului se va scrie:
|
|
(II.112) |
Scrierea
si rezolvarea ecuatiilor Lagrange este īngreunata de faptul
ca variabilele ![]() si
si ![]() nu sunt separabile.
nu sunt separabile.
Vom face urmatoarea schimbare de variabile:
|
|
(a) |
(II.113) |
|
(b) |
Se
observa ca vectorul ![]() este vectorul de
pozitie al particulei
este vectorul de
pozitie al particulei ![]() relativ la particula
relativ la particula ![]() iar vectorul
iar vectorul ![]() este vectorul de
pozitie al centrului de masa al sistemului.
este vectorul de
pozitie al centrului de masa al sistemului.
Din
relatia (II.113) ![]() si
si ![]() īn functie de
noile variabile se scriu:
īn functie de
noile variabile se scriu:
|
|
(a) |
(II.114) |
|
(b) |
Calculānd ![]() si introducānd
aceste expresii īn (II.112) obtinem:
si introducānd
aceste expresii īn (II.112) obtinem:
|
|
(II.115) |
(expresia ![]() trebuie sa
depinda de modulul vectorului
trebuie sa
depinda de modulul vectorului ![]() pentru ca din ea
vor proveni doua forte de interactie egale si de sensuri
contrare specifice pentru sisteme conservative īnchise).
pentru ca din ea
vor proveni doua forte de interactie egale si de sensuri
contrare specifice pentru sisteme conservative īnchise).
Notānd ![]() - masa sistemului -
plasata īn centrul de masa si
- masa sistemului -
plasata īn centrul de masa si ![]() - masa redusa a
sistemului
- masa redusa a
sistemului 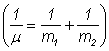 , relatia (II.115) devine:
, relatia (II.115) devine:
|
|
(II.116) |
Ecuatiile Lagrange vor fi:
|
|
(II.117) |
Dar ![]() , de unde se vede ca
, de unde se vede ca ![]() este coordonata
ciclica;
este coordonata
ciclica; ![]() va fi impulsul
centrului de masa si este constant
(se conserva).
va fi impulsul
centrului de masa si este constant
(se conserva).
Notānd ![]() viteza centrului de
masa (constanta) rezulta:
viteza centrului de
masa (constanta) rezulta:
|
|
(II.118) |
adica centrul de
masa al unui sistem de doua corpuri care interactioneaza
doar īntre ele se deplaseaza rectiliniu si uniform īn raport cu
referentialul ![]() ales.
ales.
Daca
referentialul ![]() este inertial
si sistemul de referinta legat de centrul de masa
este inertial
si sistemul de referinta legat de centrul de masa ![]() va fi tot
inertial. Īn raport cu
va fi tot
inertial. Īn raport cu ![]()
![]() , deci functia Lagrange a sistemului devine:
, deci functia Lagrange a sistemului devine:
|
|
(II.119) |
Din
aceasta expresie se vede ca problema miscarii a doua
corpuri s-a redus la miscarea unui singur corp de masa ![]() īn cāmpul de
forte cu potentialul
īn cāmpul de
forte cu potentialul ![]() , unde
, unde ![]() este vectorul relativ
de pozitie al unei particule fata de cealalta.
este vectorul relativ
de pozitie al unei particule fata de cealalta.
Miscarea
centrului de masa se va face independent de miscarea relativa a
corpurilor. Din relatia (II.119), cunoscānd forma concreta a
functiei ![]() se poate determina
se poate determina ![]() cu conditii
initiale date.
cu conditii
initiale date.
Fortele centrale sunt acele forte care actioneaza īn lungul liniei ce uneste centrele corpurilor aflate īn interactiune. Ele depind numai de distanta īntre centrele corpurilor respective.
Daca o particula se afla īntr-un cāmp de forte exterioare, cāmpul va fi central daca forta care actioneaza asupra particulei va fi orientata īn lungul liniei ce uneste particula cu un punct fix, numit centrul cāmpului de forte.
Sa consideram un sistem de referinta cu centrul īn centrul cāmpului de forte. Forta care actioneaza asupra particulei va fi:
|
|
(II.120) |
Daca
functia ![]() este dependenta
doar de modulul vectorului de pozitie
este dependenta
doar de modulul vectorului de pozitie ![]() , cāmpul va fi conservativ, adica provine dintr-un
potential
, cāmpul va fi conservativ, adica provine dintr-un
potential ![]() prin relatia:
prin relatia:
|
sau
|
(II.121.a) |
|
|
(II.121.b) |
Cāmpul
gravitational, cāmpul coulombian - sunt cāmpuri centrale. Pentru acestea
potentialul ![]() este de forma:
este de forma:
|
|
(II.122) |
Daca ![]() , deci
, deci ![]() este forta
atractiva.
este forta
atractiva.
Daca ![]() , deci
, deci ![]() este forta
repulsiva.
este forta
repulsiva.
Problema miscarii īn cāmp central a fost dezvoltata īn legatura cu miscarea planetelor īn jurul Soarelui.
Cānd
studiem fortele centrale, datorita simetriei sferice a problemelor,
este util sa folosim coordonatele polare īn spatiu (coordonatele
sferice) ![]() (fig.II.5.).
(fig.II.5.).
|
Fig.II.5 |
Legatura
īntre coordonatele carteziene ![]() si cele sferice
si cele sferice ![]() este data de
relatiile:
este data de
relatiile:
|
|
(II.123) |
Energia cinetica a unui punct material se va scrie:
|
|
(II 124) |
iar functia Lagrange va fi:
|
|
(II.125) |
Cele trei ecuatii Lagrange vor fi:
|
|
(II.126.a) |
|
|
(II.126.b) |
|
|
(II.126.c) |
Se
observa ca functia Lagrange nu depinde explicit de ![]() deci:
deci:
|
|
(II.127) |
Calculānd
pentru punctul material proiectia momentului cinetic pe axa ![]()
|
|
(II.128) |
se observa ca
impulsul ![]() canonic conjugat cu
coordonata (unghiul polar)
canonic conjugat cu
coordonata (unghiul polar) ![]() este chiar
proiectia momentul cinetic pe axa īn jurul careia se face
rotatia cu unghiul
este chiar
proiectia momentul cinetic pe axa īn jurul careia se face
rotatia cu unghiul ![]() .
.
Din
(II.127) si (II.128) rezulta ca ![]()
Teorema variatiei momentului cinetic (viteza de variatie a momentului cinetic este egala cu momentul fortelor rezultante) se va scrie:
|
|
(II.129) |
Daca
forta este centrala, momentul sau fata de centrul
cāmpului este nul, deci vectorul ![]() va fi constant (atāt
ca modul cāt si ca orientare). stiind ca momentul cinetic este
perpendicular pe planul vectorilor
va fi constant (atāt
ca modul cāt si ca orientare). stiind ca momentul cinetic este
perpendicular pe planul vectorilor ![]() si
si ![]() , rezulta ca si acest plan ramāne
acelasi īn miscarea īn cāmp central deci traiectoria particulei este plana.
, rezulta ca si acest plan ramāne
acelasi īn miscarea īn cāmp central deci traiectoria particulei este plana.
Daca
alegem ca plan al miscarii chiar planul ![]() , functia Lagrange devine:
, functia Lagrange devine:
|
|
(II.130) |
Iar
|
|
(II.131) |
Sa
gasim semnificatia fizica a acestui rezultat: consideram
planul miscarii (fig.II.6) si doua pozitii ![]() si
si ![]() ale punctului material
la momentele
ale punctului material
la momentele ![]() si
si ![]() .
.
|
Fig.II.6 |
Īn timpul ![]() raza vectoare
raza vectoare ![]() "matura"
suprafata
"matura"
suprafata ![]() cu aria:
cu aria:
|
|
(II.132) |
Viteza areolara (aria "maturata" de raza vectoare īn unitatea de timp) va fi:
|
|
(II.133) |
Deoarece ![]() , rezulta ca si viteza areolara este
constanta.
, rezulta ca si viteza areolara este
constanta.
Se poate atunci enunta legea a II-a a lui Kepler:
"Īn cāmp central de forte, raza vectoare "matura" arii egale īn intervale egale de timp"
Din expresia (II.131) obtinem:
|
|
(II.131') |
care introdus īn expresia energiei cinetice conduce la:
|
|
(II.134) |
iar energia totala va fi:
|
|
(II.135) |
De aici:
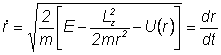
sau separānd variabilele:
|
|
(II.136) |
Aceasta se integreaza si se obtine:
|
|
(II.137) |
Scriind (II.131) sub forma:
![]()
separānd variabilele
si īnlocuind ![]() din (II.136)
obtinem:
din (II.136)
obtinem:

care se integreaza si se obtine:
|
|
(II.138) |
Relatia
(II.138) exprima dependenta ![]() si da de
fapt forma orbitei.
si da de
fapt forma orbitei.
Introducānd
![]()
si facānd
schimbarea de variabila ![]() , expresia (II.138) devine:
, expresia (II.138) devine:
|
|
(II.139) |
Notānd
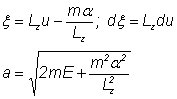
obtinem din (II.139):
![]()
sau, revenind la marimile fizice initiale:
|
|
(II.140) |
Alegānd
originea pentru unghiul ![]() astfel īncāt
astfel īncāt ![]() , obtinem:
, obtinem:
|
|
(II.141) |
Se introduc urmatoarele notatii:
|
|
(II.142) |
Cu acestea expresia (II.141) devine:
|
|
(II.143) |
Aceasta
este ecuatia unei conice (curba obtinuta prin sectionarea
unei suprafete conice cu un plan), cu focarul
īn originea axelor de coordonate; marimea ![]() se numeste parametrul conicei iar
se numeste parametrul conicei iar ![]() - excentricitatea conicei (orbitei). Se observa ca punctul
pentru care
- excentricitatea conicei (orbitei). Se observa ca punctul
pentru care ![]() are
are ![]() , care este distanta minima a punctului material
fata de centrul cāmpului. Pozitia corespunzatoare pe
orbita se numeste periheliul
orbitei.
, care este distanta minima a punctului material
fata de centrul cāmpului. Pozitia corespunzatoare pe
orbita se numeste periheliul
orbitei.
Īn
functie de valoarea excentricitatii ![]() exista patru
tipuri de curbe (orbite):
exista patru
tipuri de curbe (orbite):
elipsa,
pentru ![]() ;
;
hiperbola,
pentru ![]() ;
;
parabola,
pentru ![]() ;
;
cercul,
pentru ![]() ;
;
Din
definitia lui ![]() (relatia
(II.142)) se vede ca valorile lui
(relatia
(II.142)) se vede ca valorile lui ![]() depind de valorile
energiei
depind de valorile
energiei ![]() .
.
Pentru
"starile legate" ![]() deci
deci ![]() , traiectoria este o elipsa (miscarea este
finita).
, traiectoria este o elipsa (miscarea este
finita).
Se definesc parametrii elipsei (fig.II.7):
|
Fig.II.7 |
- semiaxa mare
|
|
(II.144) |
(depinde doar de ![]() , nu si de
, nu si de ![]() )
)
- semiaxa mica
|
|
(II.145) |
Distanta minima fata de centrul cāmpului de forte va fi:
|
|
(II.146) |
Distanta maxima (afeliu):
|
|
(II.147) |
Ţinānd
seama ca sistemul solar este stabil, ![]() , deci miscarea planetelor īn jurul Soarelui se
īncadreaza īn acest tip de miscare, astfel īncāt se poate afirma:
, deci miscarea planetelor īn jurul Soarelui se
īncadreaza īn acest tip de miscare, astfel īncāt se poate afirma:
"Miscarea planetelor īn jurul Soarelui se face pe orbite eliptice, īn unul din focare aflāndu-se Soarele". Aceasta este legea I a lui Kepler.
Īn ceea ce priveste perioada de revolutie pe orbita eliptica, folosind relatia (II.133) obtinem:
![]()
care integrata īn raport cu timpul (pe timp de o perioada) conduce la:
|
|
(II.148) |
Cum aria elipsei este:
![]()
si folosind relatiile (II.144) si (II.145) obtinem:
|
|
(II.149) |
Daca ![]() este masa unei planete,
este masa unei planete,
![]() este masa Soarelui iar
K - constanta atractiei
universale,
este masa Soarelui iar
K - constanta atractiei
universale, ![]() iar:
iar:
|
|
(II.150) |
Legea a III - a a lui Kepler se enunta atunci īn felul urmator:
"Patratul perioadei de revolutie a unei planete īn jurul Soarelui este proportional cu cubul semiaxei mari a orbitei planetei".
|