MODULATOARE sI DEMODULATOARE

MODULATOARE

sI

DEMODULATOARE

În scopul transmiterii la distanta a semnalelor se utilizeaza semnale variabile în timp cu modulatie în amplitudine (MA) sau cu modulatie în frecventa (MF).

Un semnal periodic sinusoidal numit semnal purtator (sau purtatoare)

v_p (t) = V_p cos w t

este caracterizat prin amplitudinea V _p si frecventa f ₀ (sau pulsatia

w =2 л f₀ ).

Prin intermediul semnalului purtator se pot transmite diferite informatii, exprimate prin valoarea amplitudinii purtatoarei sau valoarea frecventei.

Informatia poate fi binara ,alocând o valoare pentru zero logic si o valoare pentru unu logic. Spre exemplu daca se receptioneaza o putatoare cu amplitudinea de 10 V spunem ca s-a receptionat cifra 1, iar daca amplitudinea este de 5 V spunem ca s-a receptionat 0 - logic.

Un alt exemplu se refera la transmiterea numerica, prin linia telefonica, unde un semnal cu frecventa de 2025 kHz este interpretat drept 0 - logic , iar un semnal cu frecventa de 2225 kHz este interpretat drept 1 - logic.

În multe din aplicatii informatia este reprezentata de un semnal variabil în timp , care are mai mult de doua valori distincte (cum este în cazul semnalului binar) numit semnal modulator.

Daca semnalul modulator actioneaza asupra amplitudinii purtatoarei, frecventa purtatoarei fiind constanta, se obtine un semnal modulat în amplitudine (MA).

Daca semnalul modulator actioneaza asupra frecventei purtatoarei, amplitudinea purtatoarei fiind constanta, se obtine un semnal modulat în frecventa (MF).

Daca semnalul modulator actioneaza asupra fazei purtatoarei, amplitudinea purtatoarei fiind constanta, se obtine un semnal modulat în faza (MF).

Daca semnalul modulator actioneaza asupra fazei purtatoarei si asupra amplitudinii purtatoarei, se obtine un semnal modulat în cuadratura.

Transmiterea informatiei prin atmosfera, în prezenta unor semnale puternic pert 21421y245v urbatoare, se face cu ajutorul semnalelor modulate în frecventa, pentru ca frecventa este mai putin afectata decât amplitudinea semnalului la receptie semnalul informational va fi decodat cu mai putine erori .

10.1.Semnale modulate în amplitudine

Spunem ca un semnal este modulat în amplitudine daca semnalul util - numit semnal modulator, notat m - modifica amplitudinea V_p a purtatoarei.

Purtatoarea v_p este un semnal sinusoidal

v_p (t) = V_p cos w t

a carei frecventa (si pulsatie ω₀) este constanta.

Presupunând ca semnalul modulator este cosinusoidal

v _m(t) = V_m cos (ω_mt )

atunci semnalul v_p devine semnal purtator al informatiei pe care o contine semnalul modulator v_m si semnalul v_p modulat de v_m poate fi scris sub forma

v _MA (t) = (V _p + k _a v _m) cos (ω t )

numit semnal modulat în amplitudine cu modulatie MA normala.

Forma de unda a unui semnal modulat în amplitudine cu modulatie MA normala este prezentata figura 10.1.

Semnalul modulat în amplitudine poate fi descompus matematic

v_MA = V_p cos (ω₀t) + k_a v_m cos (ω₀t)

în doi termeni din care primul "V_pcosω₀t" reprezinta purtatoarea iar al doilea "K_av_mcosω₀t" reprezinta tot un semnal modulat în amplitudine.

S-a notat cu k _a - factorul de comprimare.

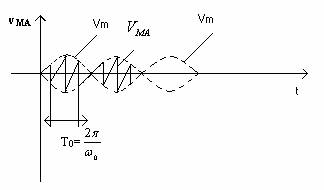
	Fig.  10.1.

Uneori nu se transmite purtatoarea v_p si spunem ca avem un semnal modulat în amplitudine cu purtatoare suprimata

v_MA.PS (t)=k_av_mcosω t .

În conditiile unui semnalul modulator armonic (v_m= V_m cosω_mt ) se poate scrie

v_MA (t) = (V_p+k_aV_mcosω_mt)cosω t =V_p(1+mcosω_mt)cosω₀t ,

putând defini gradul de modulatie

m= .

Matematic semnalul modulat în amplitudine poate fi exprimat astfel

v_MA(t) =V_pcosω₀t+mV_pcosω_mtcosω₀t

=V_pcosω t +cos(ω +ω_m)t + cos(ω -ω_m)t

încât sa fie evidentiate

V_pcosω t - purtatoarea,

cos(ω₀+ω_m)t - componenta laterala stânga

cos(ω₀-ω_m)t - componenta laterala dreapta.

Se constata ca semnalul purtator al informatiei V_m (definit prin

V_m = ) este prezent în componentele laterale ale semnalului modulat.

În figura 10.2 sunt reprezentate semnalele spectrale asociate unui semnal modulat în amplitudine (complet sau "normal" ).

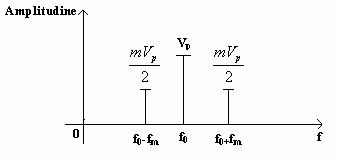
	Fig. 10.2.

Transmiterea semnalului modulat în amplitudine se poate face astfel :

- Cu modulatie normala =>

v_MA(t) = (V_p+k_av_m)cosω₀t ;

Fara purtatoare (MA- cu purtatoare suprimata) =>

v_MAPS(t) = k_av_mcosω t

Fara purtatoare si fara una din componentele laterale

(MA-PS-BLU), numita cu purtatoare suprimata si banda laterala unica =>

v_MABLU(t) = cos(ω₀+ω_m)t

v_MABLU(t) = cos(ω₀+ω_m)t ;

- Fara purtatoare cu o banda laterala si un rest al celeilalte benzi laterale.

Observatia 1 Puterea de emisie se repartizeaza

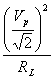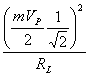P= +2=+2,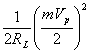

o parte pe purtatoare (primul termen din relatie) si egal pe cele doua componente laterale.

Expresia repartizarii puterii a condus la introducerea sistemelor de transmisie a semnalelor modulate fara purtatoare si numai cu una din benzile laterale (scade puterea necesara si emitatorul va avea un pret de cost mai mic).

Numai ca orice câstig (la emitator) se soldeaza cu pierderi în alta parte (la receptor), în sensul ca receptoarele pentru semnale MA-PS-BLU vor avea o schema mai complicata decât cele pentru receptia semnalelor MA normala - datorita faptului ca trebuie sa refaca purtatoarea - ceea ce conduce si la un pret de cost mai mare.

Observatia 2 Concluziile desprinse considerând un semnal modulator armonic (ca mai sus) se extind si în cazul semnalelor modulatoare de alta forma, pentru ca orice semnal modulator v _m se descompune într-o suma de semnale armonice

v _m(t) =

a caror frecventa este multiplul frecventei semnalului nesinusoidal.

Demodularea (detectia) - este procedeul de extragere a informatiei utile , adica a semnalului modulator , din semnal receptionat.

Având în vedere ca sunt mai multe procedee de transmitere a semnalului modulator , schemele electronice de detectie sunt specifice tipului de modulare.

În cazul transmisiei "normale" (atât a purtatoarei cât si a celor doua benzi laterale) se utilizeaza doua tipuri de detectoare

detectorul de valoare medie;

detectorul de valoare de vârf.

Daca se utilizeaza un sistem care nu transmite si purtatoarea (cu purtatoare suprimata) la receptie aceasta trebuie sa fie refacuta si apoi, în etapa urmatoare, sa se faca extragerea semnalului util.

Spre exemplu daca semnalul receptionat este MA-PS-BLU (cu modulatie a amplitudinii, cu purtatoare suprimata si banda laterala unica) demodularea se realizeaza cu un aparat realizat conform schemei din figura 10.3.

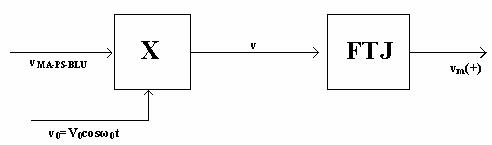
	Fig. 10.3.

Semnalul modulat

v_MA-PS = V_P m f(t) cos ω t

care în cazul modulatiei cu semnal sinusoidal ( f(t) = cosω_mt ) se poate rescrie sub forma

v_MA-PS =V_P m cos ω_mt cos ω₀t

este înmultit, în blocul "X", cu purtatoarea

v₀ = V₀cosω₀t.

La iesirea blocului de multiplicare se obtine semnalul produs notat " v "

v= v_MA-PS V_pV₀ m cos ω_mt cosω t =

v= cos ω_mt [1+cos(2ω₀t)] ,

v = cos ω_mt + cos ω_mt cos (2ω₀t)

care se compune dintr-un semnal de joasa frecventa

cosω_mt ,

si un semnal de frecventa mare

cos ω_mt cos (2ω₀t) .

Filtrul trece-jos FTJ de la iesirea circuitului de multiplicare are rolul de a permite trecerea semnalului de joasa frecventa, blocând componentele cu pulsatia 2ω₀ .

La iesirea schemei din figura 10.3 se obtine semnalul modulator a carei amplitudine depinde de amplitudinea purtatoarei V ₀ , de amplitudinea semnalului receptionat V_p si de gradul "m" de modulatie.

Modulatia în cuadratura este o modulatie atât în amplitudine si în faza unui semnal purtator. Se transmit astfel cu o singura frecventa doua semnale v_p1(t) si v_p2(t).

Se recurge la modulatia a doua semnale de aceeasi frecventa

v_p= V_p sin (ω₀t) de catre v_p1 ;

v_p= V_p cos (ω₀t) de catre v_p2 ;

dupa care cele doua semnale se compun pentru a fi transmise.

Fiecarui semnal i se asociaza fazorul (vectorul complex) corespunzator astfel

v_MA =(V_p+k_a v_m )sin ω t V_MA

v_MA =(V_p+k_a v_m )cos ω t V_MA

Nota. Se mai poate scrie v_MA2 =(V_p+k_av_m2)sin (ω₀t -).

Semnalul modulat în cuadratura este suma celor doua semnale (modulate în amplitudine)

v_c=v_MA +v_MA =V_a sinω t+V_a cosω t=V_a (sinω t+cosω t)=

v_c=V_a (sinω t+tg_ccosω₀

v_c=sin(ω t+_c)= sin(ω t+_c),

care se exprima sub forma

v_c=E_csin(ω₀t+_c) E_c =E_c.

Componentele vectorului asociat sunt functie de semnalele modulatoare, conform relatiilor

E_c= ;

tg _c = , cos =

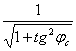
Informatia privind semnalele modulatoare v_a1,v_a2 este continuta în amplitudinea E_c cât si în faza semnalului _c.

De fapt modulatia în cuadratura este o modulatie atât în amplitudine cât si în faza semnalului modulator.

În continuare v_c se transmite MA , MA-PS sau MA-PS-BLU de fapt numai MA-PS-BLU.

Nota. Transmiterea MA-PS-BLU în conditia modulatiei în cuadratura impune cunoasterea exacta a momentului în timpul în care începe semnalul modulator , vezi figura 10.4.,pentru a avea originea unghiului _{c .}

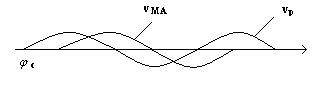
	Fig. 10.4.

Se procedeaza la refacerea putatoarei, pe baza unui semnal nemodulat transmis odata cu informatia continuta în semnalul modulat în cuadratura.

Circuite multiplicatoare analogice

Circuitele de multiplicare au rolul de a realizarea produsului a doua semnale v_x(t) si v_y(t) pentru a obtine

v (t)=k v_x(t) v_y(t).

Principiul de functionare al unui circuit de înmultire se bazeaza pe caracteristica de intrare exponentiala a tranzistorului

I_E=I_0.,

unde I_E este curentul de emitor al tranzistorului, V_BE este tensiunea

baza -emitor, iar celelalte marimi sunt constante pentru un tranzistor si o temperatura data.

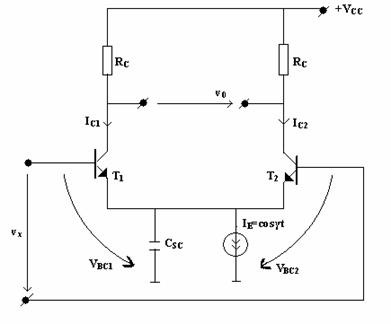
Fig. 10.5.

Daca V_BE se modifica la V_BE+∆V_BE atunci I_E se modifica de la I_E la

I_E + ∆I_E asa încât, prin diferentiere, avem

∆I_E = ∆V_BE = I₀ ∆V_BE = I_E ∆V_BE

∆I_E= ∆V_BE ,

unde V_T= este tensiunea termica a tranzistorului

În schemele de multiplicare nu se foloseste un singur tranzistor pentru modelarea ecuatiei de mai sus ci se prefera montajele diferentiale, ca în figura 10.5, pentru a realiza o compensare a variatiei parametrilor tranzistorului cu temperatura.

Fie v_x tensiunea variabila în PSF avem

I_E1 I_E2 ,

∆I_E1=

În regim variabil se poate exprima tensiunea de iesire

v =R_C (∆I_C - ∆I_C )= R_C (∆I_E + ∆I_E

v = R_C (∆V_BE -∆V_BE ) = v_x

unde

v_x =∆V_BE -∆V_BE

Se constata ca tensiunea v_x este diferenta tensiunilor din baza celor doi tranzistori. Temperatura va afecta la fel cele doua marimi, iar daca în montaj avem tranzistori identici, diferenta celor doua tensiuni nu va fi afectata de variatia temperaturii.

Tensiunea v₀=I_E v_x

reprezinta produsul a doua semnale si anume v_x cu I_E.

Curentul I_E se poate modifica conform unei a doua tensiuni v_y , spre exemplu ca în figura 10.6.

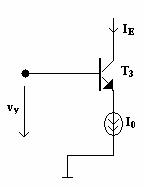
Fig. 10.6.

Tensiunea de iesire poate fi exprimata ca produs al tensiunilor

v₀= S v_x v_y.

Pe de alta parte avem

pentru v_y =0 I_E=I₀

pentru v_y0 I_E= ∆V_BE = v_y

ceea ce conduce la expresia

v₀= v_x v_y= S v_x v_y

Deoarece curentul I_E pleaca de la zero montajul de mai sus nu functioneaza pentru tensiuni negative .

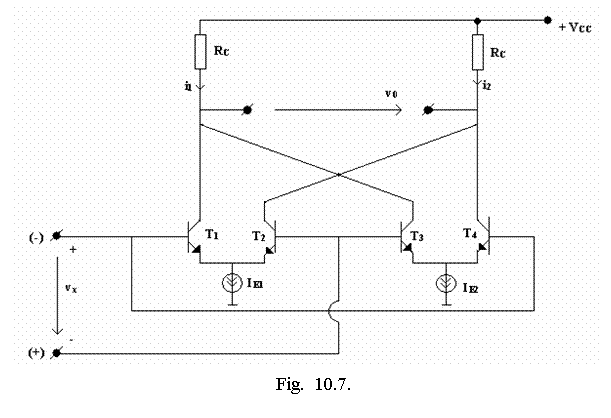
Pentru polaritati atât pozitive cât si negative ale tensiunilor de intrare se completeaza montajul, ca în figura 10.7, cu elemente care sa permita functionarea multiplicatorului si pentru tensiuni negative.

Pentru v_x >0 tranzitorii T₁ si T4 vor fi în conductie, pe baza acestora aplicându-se un semnal pozitiv, iar pentru v_x <0 tranzitorii T₂ si T₃ vor fi în conductie.

Tensiunea de iesire se exprima în functie de curenti

v =R_C (i -i )= R_C (i_C +i_C ) - R_C(i_C +i_C

v =R_C (i_C -i_C ) - R_C (i_C -i_C

v = R_C v_x (I_E -I_E

unde

i_C -i_C = v_x ; i_C -i_C =v_x

Cea de-a doua tensiune v_y (cu care se multiplica v_x) trebuie sa modifice diferenta curentilor I_E1 , I_E2

Schema completa a multiplicatorului tensiunilor v_x si v_y , pentru orice polaritate a acestor tensiuni, este prezentata în figura 10.8.

Fara tensiune aplicata la bornele v_y sursa de curent furnizeaza curenti de emitor egali pentru tranzistori T₅ si T₆ asa încât avem

I_E1=I_E2=.

Tensiunea v_y blocheaza în alternanta pozitiva tranzistorul T₆ si curentul furnizat de sursa este preluat de tranzistorul T₅ si

∆I_E5=.

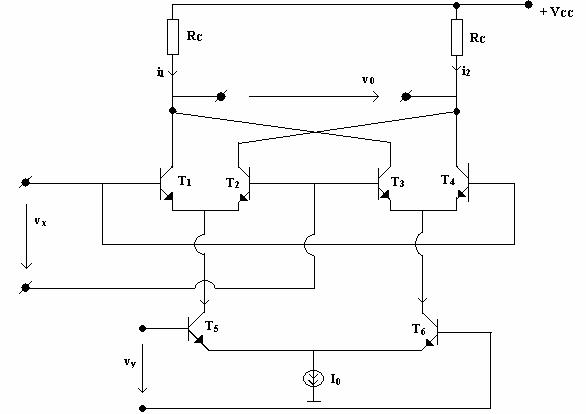
	Fig. 10.8.

Sursa de curent poate fii realizata cu un tranzistor, ca în figura 10.9, a carui baza se gaseste la potential constant fata de emitor.

I₀=I_S()

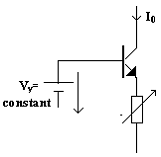
	Fig. 10.9.

Detectorul semnalelor MA cu circuit de multiplicare

Detectorul de semnale MA cu circuit de multiplicare este prezentat în figura 10.10.

Semnalul modulat în amplitudine de forma

v_i=V_i (1+v_m)cosω₀t,

modifica, în functie de polaritate valoarea curentului de emitor a tranzistorului Q₂₂ sau Q₂₃.

Semnalul

v_p=V_pcosω t

reprezinta purtatoarea nemodulata, care printr-un circuit de limitare este adusa la o forma trapezoidala, aproape dreptunghiulara

Purtatoarea poate fi descompusa într-o fundamentala si o serie de armonici

v_p=cosω₀t+cos(2k+1)ω₀t.

Tensiunea de iesire va contine numai armonicile impare

v_out=k_m(1+cosω t+cos3ω t+....)

si fundamentala purtatoarei.

Prin intermediul unui filtru trece - jos se elimina atât fundamentala cât si armonicile

FTJ v_out= V_i (1+v_m(t)).

Se constata ca la iesire s-a obtinut semnalul modulator a carei amplitudine este functie de câstigul multiplicatorului

k_m==

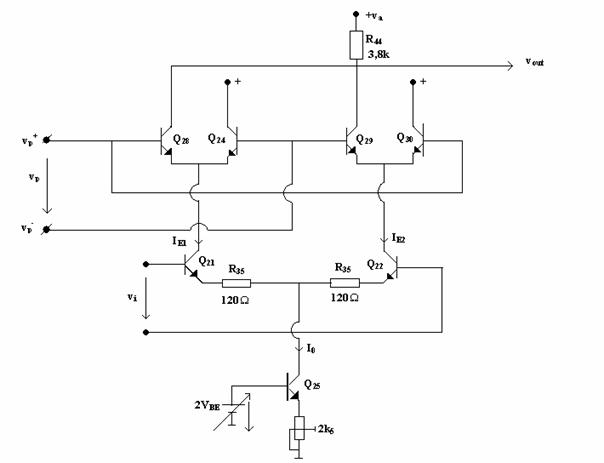
	Fig. 10.10.

Circuite pentru demodularea sincrona a semnalelor modulate în frecventa

Demodularea sincrona a semnalelor modulate în frecventa

Purtatoarea de frecventa f₀ (pulsatie ω₀ )

v_p=V_psin(ω₀t+_p)

si _pfaza initiala constanta sufera o modulatie a frecventei sub actiunea semnalului modulator astfel încât deviatia de frecventa se exprima

f=k_mv_m(t) ω=kv_m(t)

în functie de semnalul modulator.

Semnalul modulat în frecventa are expresia

v_MF(t)=V _psin (ωt+_p)

cu ω=ω₀+ω.

Domeniul de variatie al semnalului modulator în timp real t_inf..t_sup determina o modificare a pulsatiei ω în domeniul

ω₀-ω_mx<ω<ω₀+ ω_mx

Faza semnalului se calculeaza cu relatia

(t)==ω₀t+ ;

(t),

ceea ce conduce la o alta exprimare a semnalului modulat în frecventa

v_MF(t)=V_psin[ω t+] .

Pentru extragerea semnalului modulator semnalul v_MF este puternic limitat, ca în figura 10.11, pentru ca perturbatiile care afecteaza amplitudinea semnalelor sa fie eliminate .

Semnalul limitat în amplitudine, modulat în frecventa poate fi exprimat prin dezvoltarea în serie

v_MFv₁=V_p

unde s-a definit unghiul prin relatia

(t)= .

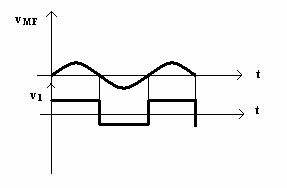
	Fig. 10.11.

Circuitul demodulator actioneaza asupra semnalului modulat în frecventa

v_MF=V_p sin(ωt+)

unde ω₀-ω_max<ω<ω₀+ω_{max ,}

=constant.

Principiul consta în transformarea modulatiei frecventei intr-o modulatie a fazei semnalului.

Semnalul v_MF limitat puternic , devine un semnal aproape dreptunghiular si se aplica unui circuit RLC paralel, cu schema în figura 10.12.

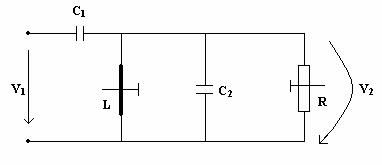
	Fig. 10.12.

Caracteristica de frecventa si caracteristica fazei pentru circuitul RLC sunt prezentate în figura 10.13.

Fig. 10.13.

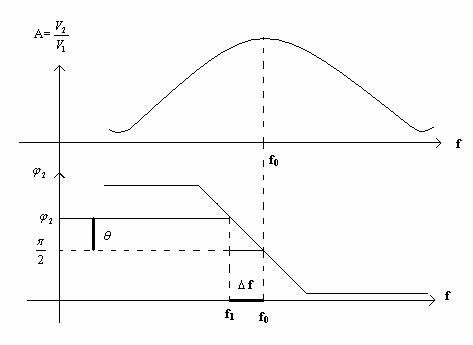
Caracteristic circuitului RLC este ca la frecventa de rezonanta f₀=, (C=C₁+C₂ ) tensiunea v₂=V₂ sin (ωt+) este defazata cu fata de tensiunea v₁=dreptunghiulara (V₁sinω₀t) aplicata circuitului.

În figura 10.14 sunt evidentiate doua puncte si anume

- daca v₁ = V₁( f₀ , 0) v₂ = V₂ ( f₀, ),

- daca v₁ = V₁(f₁,0) v₂ = V₂(f₁, =+) .

Deci v₂ are aceeasi frecventa ca v₁ dar depinde de deviatia de frecventa proportionala (f₁=f₀+f) .

Conform caracteristicii se poate scrie

=k₀f ; =+= +k₀f

si

v =V_psin(ω₁t+)=V₂sin(ω₁t+ +k₀ f)

v =V₂cos(ω₁t+ k f) .

Demodularea realizeaza produsul semnalelor v₁,v₂ urmate de un FTJ care blocheaza frecvente mai mici ca f₀, astfel

v v =V₁Vsinω₁t cos(ω₁t+)= [sin(2ω₁+)+sin()]=

-sin(kf) - = -k_θf

Schema demodulatorului MF

În figura 10.14 este prezentata schema unui demodulator MF.

Fig. 10.14.

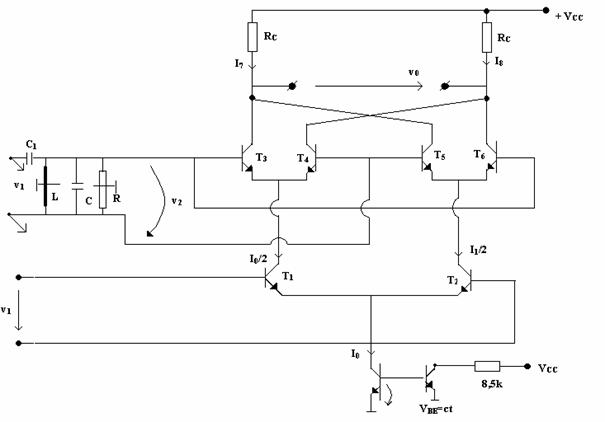
Curentul de referinta, realizat cu sursa de curent constant realizata cu doi tranzistori, are expresia

I_0==.

Comparând schema din figura 10.15 cu schema din figura 10.10, constatam ca tensiunea v₂ este formata din tensiunea v₁ de circuitul oscilant paralel RLC.

Rezistorul si inductivitatea sunt ajustabile (inductivitatea se modifica prin modificarea circuitului magnetic) în scopul acordarii frecventei de oscilatie a circuitului oscilant pe frecventa purtatoarei.

Tensiunea v₁ repartizeaza, în functie de polaritate, curentul generatorului catre unul din grupurile de tranzistori T₃ T₄ sau T₅ T₆ . Valoarea tensiunii v₁ modifica unul din curentii I₇ sau I₈.

Cuplajul la tensiunea v₁ a circuitului RLC se face prin condensator pentru a nu afecta functionarea în curent continuu a tranzistorilor T₃ T₄ sau T₅ T₆ .

Formele de unda sunt desenate, în figura 10.15, pentru frecventa de rezonanta, când defazajul între v₁ si v₂ este ₂=

La f₀(₂=) avem I₇ =I₈=. Daca f₁>f_{0 2} creste fata de ₂ =+f . Daca f₁<f_{0 2} scade .

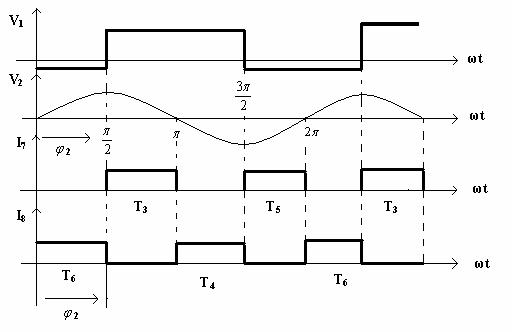
	Fig. 10.15.

Scaderea f₁ fata de f₀ implica f₁=f₀-f ceea ce determina o scadere a unghiului ₂ =-f scade timpul de conductie al curentului I₈ si creste timpul de conductie al curentului I₇.

I = =2==

I =2=()

Tensiunea de iesire este

V =R_C (I -I )= k()= k()

V =k()

V =kk_θf.

Ceea ce înseamna ca daca faza ₂ se modifica în functie de frecventa, tensiunea este proportionala cu deviatia de frecventa

V =k_vf ; =+f

Se verifica faptul ca tensiunea de iesire v₀ depinde de valoarea tensiunii de alimentare a circuitului (prin I₀) , motiv pentru care se impune ca tensiunea sursei de curent continuu sa fie foarte stabila.