Calculul complexitatii in cazul sortarii prin insertie

Probleme

1. Calculul complexitatii in cazul sortarii prin insertie

S se calculeze T(n) pentru algoritmul de sortare prin insertie.

Notatii: A - tabloul de sortat (numere intregi)

n - lungime[A] 10, 7, 5, 2,1

c_i - costul instructiunii din linia respectiv (de obicei in unitati de timp)

t_j numarul de executii ale testului din linia 4 (pentru fiecare j = 2,3lungime[A]

Atunci: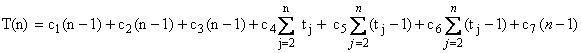

Pentru a calcula efectiv T(n) vom considera 3 cazuri.

1^o. Cazul cel mai favorabil cand A e sortat crescǎtor

Pentru fiecare j = 2,3lungime[A] avem Temp ³ A[i] Þ t_j = 1.

Deci

= an + b = W (n)

(o functie liniarǎ de n)

2^o. Cazul cel mai nefavorabil cand A e sortat descrescǎtor

Pentru fiecare j = 2,3lungime[A] avem cheie < A[i] Þ t_j = j

iar 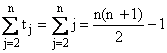si

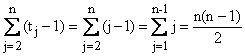
Deci:

= an² + bn+c = O(n²) (o functie polinomiala patratica de n)

3^o. Cazul mediu cand

Pentru fiecare j = 2,3lungime[A] avem t_j = j/2, adica jumatate din elementele secventei sunt sortate crescator, o presupunere destul de realista

iar si

Deci an² + bn+c = O (n²) (o functie polinomiala patratica de n)

Concluzie: T(n)=O(n²)

2. Sortarile fara comparatii intre elementele secventei

a)      Sortarea distributiilor (MathSort), determinarea T(n)=O(n), deci complexitate liniara

b)      Sortarea prin evaluarea cifrelor (RadixSort), determinarea T(n)=O(n), deci complexitate liniara

3. Sa se determine complexitatea (T(n)=?) pentru algoritmul

Pt i 1, n executa C₁

j i C₂

CatTimp j ¹ 0 executa C₃

j j div 2 C₄

SfCatTimp

SfPt

Avem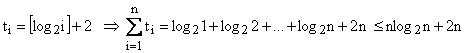

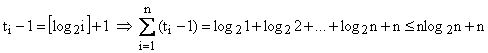
Þ T(n) = (c₁+c₂)n + (c₁+c₂) + c₃(nlog₂n + 2n) + c₄(nlog₂n +n)=

= (c₁+c₂+2c₃+c₄) n + (c₃+c₄) nlog₂n + (c₁+c₂) = O(n *log₂n).

4. Turnurile din Hanoi

Procedura Hanoi(n,A,B,C)

Daca n=1

Atunci @ Se muta discul 1 de pe A pe B

Altfel Hanoi (n-1, A,C,B)

@ Se muta discul n de pe A pe B

Hanoi (n-1,C,B,A)

SfDaca

SfProcedura

Recurenta dedusa este

Rezolvare: iteram si adunam membru cu membru apoi reducem:

T(n) = 2T(n-1) + 1

2T(n-1) = 2²T(n-2) + 2

2²T(n-2) = 2³T(n-3) + 2²

2^n-2 T(2) = 2^n-1 T(1) + 2^n-2

^{__________ ______ ____ _______}

T(n)= 1 + 2 + 2² + +2^n-2 + 2^n-1 =

5. Probleme pentru teorema Master.

Reamintim metoda Master

Aceasta metoda se aplica problemelor recursive care au timpul de executie de forma:

Avem 3 cazuri (demonstrate in CORMEN, THOMAS H. LEISERSON, CHARLES

RIVEST,  RONALD R.: Introducere in algoritmi. Cluj-Napoca: Editura Computer Libris Agora,

2000).

1^o Daca pentru o anumita constanta e Þ

2^o Daca Þ

3^o Daca , pentru o anumita constanta e > 0, si daca (numita si conditie de regularitate) pentru o constanta c si n suficient de mari, atunci

Observam ca practic se compara f(n) cu si solutia o va da cea mai mare dintre ele; f(n) trebuie sa fie polinomial mai mica (in primul caz) si polinomial mai mare (in cazul 3) decat .

Sa se rezolve:

T(n) = 4T(n/2) +n; T(n) = 4T(n/2) +n²;

T(n) = 4T(n/2) +n³; T(n) = 2T(n/2) +n³;

T(n) = T(9n/10) +n; T(n) = 16T(n/4) +n²;

T(n) = 7T(n/3) +n²; T(n) = 7T(n/2) +n²;

T(n) = 2T(n/4) +; T(n) = 3T(n/2) +nlog₂n;

T(n) = 2T(n/2) +n/log₂n;  T(n) = T(n-1) +n;

T(n) = T() +1 T(n) = T(n-1) +1/n;

T(n) = T(n-1) +log₂n;  T(n) = T() +n;

T(n) = T(n/2) +Q cautare binara

6. Alte probleme

a)      Problema steagului olandez (bile de 3 culori, amestecate la inceput, trebuie puse compact pe culori distincte, parcurgand o singura data secventa de bile)

b)      Sa se arate ca parcurgand o singura dat o secventa de n elemente se poate determina atat valoarea minima cat si valoarea maxima efectuand cel mult 3*[n/2] +C comparatii unde C este o constanta ce trebuie determinata.

c)      Algoritmi pe o tabla de operatii (asociativitate, comutativitate, elemente neutru, element invers ) cu determinarea complexitatii, se poate da ca si tema de casa;

d)      Pentru urmatoarea secventa de pseudocod sa se numere cate atribuiri se fac:

Pentru i ← n-2,-2,-1 executa // n intreg

Pentru j ← i+3,n executa

@ o(una) atribuire

SfPentru

SfPentru

Rezolvare posibila:

Nr(atribuiri) =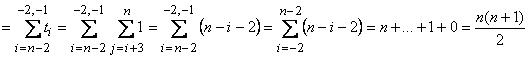

Doar pentru n ≥1. Pentru valorile lui n <1 avem nr(atribuiri)=0.

Altfel: vom incerca sa dam valori succesive lui n apoi sa vedem ce multimi parcurg indicii i si j;

Pentru inceput observam ca trebuie ca n-2≥-2, pentru ca sa se intre in primul ciclu deci n≥0. Concluzie pentru valorile lui n I nr(atribuiri)=0.

In tabelul urmator vom da valorile indicilor i si j

Concluzia nr(atribuiri)=n(n+1)/2, pentru n ≥1.

7. Se executa pe doua calculatoare 2 programe de sortare pentru a sorta 1 milion (10⁶) de numere.

Primul calculator este un SuperComputer(notat Super) care executa 10⁸ operatii pe secunda, iar al 2-lea este un PC care executa 10⁶ operatii pe secunda.

Pe Super s-a codificat un program de sortare care are T(n) = 2n², iar pe PC s-a impementat un program cu T(n) = 50nlog₂n. Sa vedem ce nevoie de timp are fiecare computer:

Pentru Super:

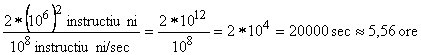
Pentru PC:

8. Despre Heap-ul binar.

ReMakeHeap - pentru intretinerea proprietatii de heap;

BuildHeap - genereaza un heap dintr-un vector neordonat, furnizat la intrare. 

HeapSort  - ordoneaza un vector in spatiul alocat acestuia.

Reconstituirea proprietatii de Heap (ReMakeHeap)

-se presupune ca la apel pentru nodul i, subarborii cu radacina STANGA(i) si DREAPTA(i) sunt

heap-uri.

-sarcina procedurii este de a ,"scufunda" in HEAP pe A[i] astfel incat subarborele, care are

radacina valorii A[i] sa devina un heap.

Procedure ReMakeHeap(A,i)

l ← STANGA(i) // l=2i

r ← DREAPTA(i) // l=2i+1

Daca l ≤ DimHeap[A]si A[l] > A[i]

Atunci maxim ← l

Altfel maxim ← i

SfDaca

Daca r ≤ DimHeap[A] si A[r] > A[maxim]

Atunci maxim ← r

SfDaca

Daca maxim ≠ i

Atunci

A[i] ↔ A[maxim]

ReMakeHeap (A,maxim)

SfDaca

SfProcedura.

Complexitate

Dimensiunea unui subarbore binar este cel mult 2n/3, pentru un arbore binar de n noduri.

Deci T(n)≤T(2n∕3)+Θ(1) ══> T(n)=0(log₂n)

Suntem in cazul 2 al teoremei master:

a=1, b=3/2, f(n) = Θ(1)

══> T(n)=0(log₂n) sau pentru inaltimea h avem O(h).

Dam in continuare procedura de construire a unui heap dintr-un vector:

Procedure BuildHeap(A)

DimHeap[A] ← Lungime[A]

Pentru i ← ,1,-1 executa

ReMakeHeap(A,i)

SfPentru

SfProcedura.

Complexitate

Pentru o inaltime h oarecare (interioara, inaltimea arborelui fiind log₂n) a unui arbore binar

aproape complet de n noduri, exista cel mult noduri de inaltime h.

Avem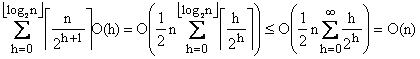

deoarece:

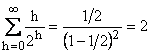, aplicand formula 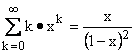, pentru x=1/2.

Dam in continuare procedura de sortare a unui heap:

Procedure HeapSort(A)

BuildHeap(A)

Pentru i ← ,2,-1 executa

A[1] ↔ A[i]

DimHeap[A] ← DimHeap[A]-1

ReMakeHeap(A,1)

SfPentru

SfProcedura.

Complexitatea este evidenta: T(n) = O(n) +O(nlog₂n) = O(nlog₂n)

Aplicatii la vector (array)

TAD Polinom. Sa se scrie doi algoritmi pt. calculul valoarea unui polinom intr-un punct .si pt suma polinoamelor. Se cere ca unul dintre algoritmi sa aiba complexitatea de ordinul Q(n), iar celalalt - de ordinul: Q(n²).

Discutie despre DS folosita:

Pt pol de gr. N folosesc un array de n+1 elem

Sau folosesc un vector dynamic cu elemente (grad,valoare)

10. Propunere de tema. Se considera problema de a determina daca un sir arbitrar de numere contine cel putin 2 termeni egali. Aratati ca exista un algoritm care rezolva aceasta problema in Q(n log(n)).