Densitatea Normala

Densitatea Normala

Curba Gauss, sau clopotul lui Gauss a jucat în istoria stintei si joaca si acum un rol foarte important, iar în medicina foarte multi parametri legati de organismul uman, de legile fundamentale ale viului, sunt repartizati dupa aceasta curba. Ce este de fapt aceasta curba?

Formula curbei lui Gauss, este:

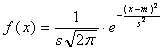
Se observa ca aceasta curba depinde de doi parametri, m si s, si ea este perfect determinata în momentul în care se cunosc acesti parametri. Deoarece curba descrie repartitia unei populatii, cei doi parametri reprezinta media (m) si abaterea standard (s) ale populatiei respective.

Graficul din figura 6.6, care este graficul unei curbe Gauss, ne arata ca, spre centru probabilitatile sunt cu atât mai mari cu cât suntem mai aproape de medie, iar spre margini probabilitatile scad apropiindu-se de zero pe masura ce ne îndepartam din ce în ce mai mult de medie. Curba 141w2219b este simetrica, niciodata însa simetria nu este perfecta pe o histograma particulara sau pe un poligon al freceventelor, dar curba ideala este perfect simetrica. Subliniem ca prin curba ideala întelegem curba catre care se îndreapta poligonul frecventelor când numarul de cazuri tinde la infinit iar lungimea claselor se apropie de zero. Uneori, graficul functiei este denumit "clopotul lui Gauss" datorita formei lui deosebite, asemanatoare unui clopot.

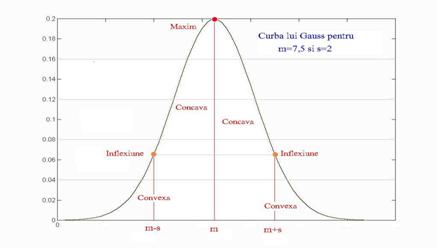
Figura 6.6 Curba repartitiei normale, sau curba lui Gauss. Are un maxim în dreptul mediei, doua puncte de inflexiune (în dreptul valorilor m-s si m+s), tinde la zero pe masura ce ne îndepartam de medie la stânga si la dreapta

În analiza matematica se arata ca graficul acestei functii, cel din figura 6.6, are un maxim pentru x=m si doua puncte de inflexiune (în care devine din concava convexa), la m-s si la m+s.

Curba normala mai este cunoscuta sub denumirea de legea Gauss-Laplace sau legea normala si apare pentru prima data într-o lucrare a matematicianului Moivre (1667 - 1754), apoi în lucrarile lui Pierre Simon de Laplace (1749 - 1827). Celebra este facuta de lucrarile matematicianului Gauss (1777 - 1855). Utilitatea acestei repartitii se datoreaza mai multor cauze, printre care:

Multe fenomene aleatoare din natura se supun exact sau aproximativ acestei legi. Astfel, deviatiile stânga-dreapta de la medie ale erorilor de masurare urmeaza aceasta lege simetrica si cu proprietatea ca, erori din ce în ce mai mari sunt din ce în ce mai rare.

O teorema foarte importanta, teorema limita centrala, asigura acestei repartitii un rol privilegiat prin faptul ca suma unui numar mare de variabile aleatoare independente una de alta, dar identic repartizate, este repartizata Gauss sau aproximativ Gauss. Aceasta teorema ne asigura de exemplu, de faptul ca, media calculata pe un lot are o repartitie Gauss sau apropiata.

S-a demonstrat ca multe repartitii empirice întâlnite în practica pot fi aduse la o repartitie Gauss prin transformari simple si în felul acesta devin mai usor de studiat.

Trebuie retinut ca repartitia Gauss are urmatoarele proprietati importante:

Este simetrica fata de media m

Are doua puncte de inflexiune, la m-s si m+s

Are maximul pentru x = m

Are doua cozi spre + si - infinit care se apropie din ce în ce mai mult de axa orizontala, fara sa o atinga

Mediana si modul, coincid cu media

Deoarece mediana coincide cu media, jumatate din aria de sub curba se afla în stânga mediei si jumatate în dreapta. Deci, într-o populatie repartizata Gauss, 50% din indivizi sunt sub medie si 50% peste medie

Aria cuprinsa între curba si axa orizontala este 1 indiferent de medie si de deviatia standard.

Aria cuprinsa între curba, axa orizontala si doua verticale în dreptul numerelor a si b, este probabilitatea ca, extragând aleator un individ din populatie si facând masuratoarea pe acel individ, valoarea obtinuta x, sa fie între a si b (Vezi figura 6.7).

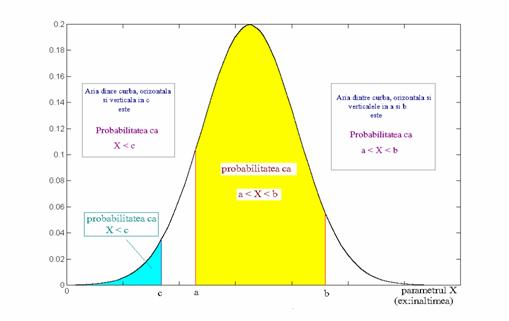
Figura 6.7 Aria cuprinsa între curba, axa orizontala si doua verticale în dreptul numerelor a si b, este probabilitatea ca, extragând aleator un individ din populatie si facând masuratoarea pe acel individ, valoarea obtinuta x, sa fie între a si b

Repartitia Gauss, este de fapt o famile de repartitii ce depinde cei doi parametri: media si deviatia standard. În figura 6.8, sunt desenate câteva curbe de repartitie Gauss, mai mult sau mai putin aplatizate, dupa cum deviatia standard este mai mica sau mai mare.

Figura 6.8 Diferite curbe Gauss mai mult sau mai putin aplatizate, aplatizarea fiind data de valoarea deviatiei standard, s. Cu cât valoarea lui s este mai mare, cu atât curba este mai aplatizata. Când s ia valori mici, curba este mai înalta.

Avem de asemenea, o infinitate de curbe Gauss care au aceeasi deviatie standard dar au medii diferite. Ele sunt identice ca forma, doar sunt localizate diferit în plan si pot fi suprapuse prin translatii stânga-dreapta. În figura 6.9, sunt desenate câteva curbe Gauss care difera numai prin medie. Având toate aceeasi deviatie standard, au aceeasi aplatizare.

Figura 6.9 Curbe Gauss cu aceeasi deviatie standard. Ele sunt la fel de aplatizate si pot fi suprapuse prin translatii stânga-dreapta.

Daca fixam media dar permitem orice deviatie standard, exista o infinitate de curbe Gauss care au aceeasi medie. Ele sunt localizate identic stânga-dreapta, dar difera prin aplatizare mai mult sau mai putin accentuata. În figura 6.10, sunt desenate 3 curbe Gauss cu aceeasi medie si cu deviatiile standard 1, 1.2 si 1.5.

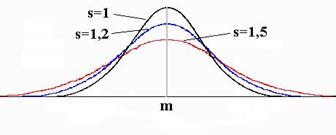
Figura 6.10 Trei curbe Gauss cu aceeasi medie si deviatii standard diferite

Un caz special de curba Gauss se obtine daca m=0 si s=1, caz în care functia f are forma:

expresie care are graficul în figura 6.11. Pentru x=0, valoarea functiei este aproximativ 0,4, deoarece e⁰=1. Valorile lui f scad foarte repede odata cu cresterea lui x, fie în sensul pozitiv, fie în sensul negativ. Aceasta deoarece expresia lui f se mai scrie ca:

Dupa cum se stie, exponentiala este una din functiile care cresc extrem de rapid (crestere exponentiala), ceea ce face ca f(x) sa scada extrem de repede cu cresterea lui x. De exemplu, daca x = 3, sau x = -3, atunci f(x)=0,004, aproximativ. Pentru valori ale lui x mai mari decât 3 sau mai mici decât -3, valoarea lui f este neglijabil de mica (vezi subcapitolul 6.3 pentru amanunte privind aceasta repartitie speciala).

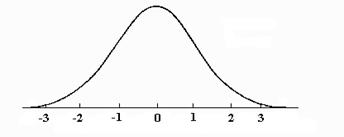
Figura6.11 Curba lui Gauss corespunzatoare la m=0 si s=1. Are un maxim egal cu aproximativ 0,4. Se observa ca scade extrem de repede odata cu îndepartarea de 0. Valorile ei dincolo de 3 si de -3 sunt neglijabil de mici. Se mai numeste curba Gauss standard

Asa cum am aratat, repartitia normala sau Gaussiana este des întâlnita în studiul fenomenelor biologice si are unele proprietati utile. În biologie, una din problemele importante care se pun în legatura cu datele pe care le masuram este aceea daca se încadreaza sau nu în limitele de normalitate. Repartitia normala ne poate ajuta sa dam un raspuns acestei întrebari, cel putin pentru acele date care sunt distribuite normal. Daca o variabila are repartitie Gauss, atunci se poate stabili cât de plauzibila este media si deviatia standard gasite prin masuratori pe un lot si se pot face comparatii cu mediile care ar trebui sa fie obtinute si care sunt cunoscute din literatura de specialitate (vezi capitolul despre esantionare si cel dsepre teste statistice pentru amanunte).

Cunoscând despre o variabila ca are repartitie Gauss, se pot deduce unele afirmatii despre valorile pe care le poate lua. Cum folosim aceasta repartitie pentru a deduce anumite concluzii despre variabila care ne intereseaza? Dupa cum am mai afirmat, pentru o variabila repartizata normal, procentul din populatie situat între doua limite date este aria cuprinsa între curba Gauss, axa orizontala si cele doua verticale la limitele fixate. De obicei se considera intervalele în jurul mediei, simetrice, cu limite situate la o distanta de una sau mai multe abateri standard de medie. Astfel, se poate demonstra ca:

În intervalul m-s, m+s se afla aproximativ 68% din indivizii unei populatii repartizate normal (vezi figura 6.12). Aceasta însa nu este o majoritate suficient de mare pentru a fi aproape de siguranta daca ne întrebam între ce limite sunt situate valorile masurate pentru indivizii din populatie.

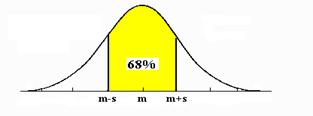
Figura 6.12 Între m-s, m+s se afla aproximativ 68% din indivizii unei

populatii repartizate normal

De aceea se ia cel mai adesea în considerare intervalul m-2s, m+2s în care se situeaza aproximativ 95% din indivizii unei populatiei repartizate normal. Acest interval este suficient de larg si cuprinde o majoritate zdrobitoare a populatiei asa ca este cel mai indicat sa fie folosit ca interval de normalitate.

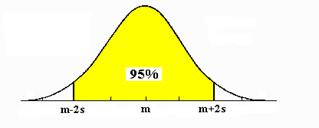
Figura 6.13 Între m-2s, m+2s se afla aproximativ 95% din indivizii unei

populatii repartizate normal

Uneori, se iau intervale mai cuprinzatoare, ca m-3s, m+3s interval în care se situeaza peste 99% din populatia considerata (vezi figura 6.14).

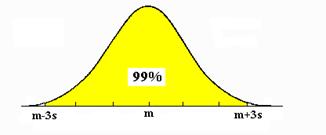
Figura 6.14 Între m-3s, m+3s se afla peste 99% din indivizii unei

populatii repartizate normal

Chiar daca se considera de obicei ca pentru variabilele folosite uzual în practica medicala valorile medii sunt cunoscute si se cunosc si asa-numitele intervale de normalitate, în realitate se cunosc doar foarte bune aproximari ale lor obtinute pe baza unor studii foarte atente, pe loturi largi.valorile reale ale mediei si deviatiei standard pentru o populatie distribuita normal, notate cu m si s, sunt aproximate cu si s care sunt indicatorii medie si abatere standard pentru un lot extras din populatia respectiva.

Cum se stabileste cât de bune sunt aceste aproximari, care se mai numesc estimari, se va vedea în capitolul 7. Oricum, se folosesc din plin proprietatile distributiei Gaussiene.