Ecuatii si inecuatii de gradul intai

Ecuatii si inecuatii de gradul întâi

VI.1. Ecuatii de gradul întâi sau ecuatii afine

ax + b = 0, a,b,x R

Fie S multimea de solutii a acestei ecuatii. Dacã

a 0, x = (solutie unicã). S = .

a = 0 si b 0, ecuatia nu are solutii: S = ;

a = 0 si b = 0, orice numãr real x este solutie a ecuatiei afine date; S = R.

Semnul functiei afine f:R R, f(x) = ax + b, a 0

Graficul functiei de gradul întâi va fi o linie dreaptã.

y

A(0,b)

x

B(,0)

VI.2. Inecuatii de gradul întâi sau ecuatii fine

Cazul 1. ax + b > 0, a,b,x R. Fie S multimea solutiilor. Dacã:

a > 0, S =(, + );

a < 0, S = (- ,);

a = 0, b > 0, S = R;

a = 0, b = 0, S = .

Cazul 2. ax + b = 0, a,b,x R. Dacã:

a > 0, S = (+ ,]

a < 0, S = [,+ )

a = 0, b = 0, S = R;

a = 0, b > 0, S = .

Inecuatiile ax + b < 0 si ax + b 0 se reduc la cele douã cazuri (prin înmultirea inecuatiei respective cu -1 si schimbarea sensului inegalitãtilor).

VI.3. Modului unui numãr real

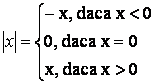
Proprietãti:" x,y R, avem:

1. ;

2. ;

sau ;

R;

;

;

;

;

;

.

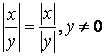Ecuatii si inecuatii fundamentale, care contin modulul:

, (a,b,x R, S = multimea solutiilor)