Progresii

Progresii

Progresii aritmetice

Def.Sirul pentru care fiecare termen al sau , incepand cu al doilea , se obtine din precedentul prin adaugarea aceluiasi numar r se numeste progresie aritmetica.

Deci este o progresie aritmetica daca avem relatia de recurenta .

Pentru a proba ca sirul este o progresie aritmetica trebuie aratat ca = constant.

Orice problema cu progresie aritmetica poate fi reformulata cu ajutorul lui si r.

Notatie :

Proprietatile progresiei aritmetice

1) (monotonia).Progresia aritmetica este un sir :

- strict crescator , daca ratia r > 0 ;

- strict descrescator , daca ratia r < 0.

2) (formula termenului general) Daca sirul este o progresie aritmetica avand primul termen si ratia r , atunci termenul general are forma ;.

Sirul este o progresie aritmetica daca si numai daca orice termen al sau , incepand cu al doilea , este medie aritmetica a termenilor vecini lui , adica daca .

Daca numerele sunt in progresie aritmetica , atunci :

Suma oricaror doua numere egal departate de numerele extreme () este egala cu suma numerelor extreme ().

5) (suma primilor n termeni)Daca este o progresie aritmetica , atunci :

;

Suma primilor n termeni ai unei progresii aritmetice este egala cu produsul dintre semisuma termenilor extremi si numarul termenilor sumei.

Obs.1)

2) ; .

Scrierea convenabila a 3 termeni in progresie aritmetica:

Scrierea convenabila a 4 termeni in progresie aritmetica :

Scrierea convenabila a 5 termeni in progresie aritmetica:

Progresia geometrica

Def.Sirul cu 0 (primul termen)pentru care fiecare termen al sau , incepand cu al doilea , se obtine din precedentul prin inmultirea cu acelasi numar q 0 se numeste progresie geometrica.Numarul q se numeste ratia progresiei.

Daca este progresie geometrica daca avem relatia de recurenta : ; .

Pentru a proba ca sirul este progresie geometrica daca = constant , .

Proprietatile progresiei geometrice

1) (monotonia) Fie o progresie geometrica de ratie q.

Daca - > 0 si q > 1 , atunci este strict crescator : ;

- > 0 si q (0 ,1) , atunci este strict descrescator : ;

- < 0 si q > 1 , atunci este strict descrescator;

- < 0 si q (0 ,1) , atunci este strict crescator.

2) (formula termenului general) Daca sirul este progresie geometrica de ratie q , atunci termenul general , are forma .

Sirul cu termenii nenuli este progresie geometrica daca si numai daca pentru orice termen al sau , incepand cu al doilea avem : ,.

Daca numerele sunt in progresie geometrica, atunci  .

Produsul oricaror doua numere egal departate de numerele () este egal cu produsul numerelor extreme (.

5) (suma primilor n termeni) Daca este progresie geometrica de ratie q , atunci :

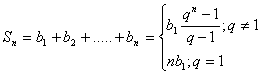
Scrierea convenabila a 3 termeni in progresie geometrica :

Scrierea convenabila a 4 termeni in progresie geometrica :

Scrierea convenabila a 5 termeni in progresie geometrica :