ALTE DOCUMENTE
|
||||||||||
LABORATOR 5
EsANTIONAREA SEMNALELOR
Deoarece semnale de interes practic sunt analogice, pentru a prelucra semnalele cu ajutorul procesoarelor numerice este nevoie de a le transforma în secvente, motiv pentru care se impune discretizarea variatiei lor în timp prin esantionare. Nu numai semnalele anaologice pot fi esantionate ci si cele discrete. Exista mai multe metode de a esantiona un semnal analogic. În continuare se considera cazul esantionarii periodice sau uniforme care este cea mai întalnita în practica. Aceasta este descrisa de 19119r178t relatia:
![]()
unde x[n] este semnalul discret obtinut prin retinerea valorilor semnalului analogic xa(t) la fiecare T secunde.
Intervalul de timp T dintre doua esantioane succesive se numeste perioada de esantionare sau interval de esantionare. Inversa acestei marimi (1/T=Fs) se numeste viteza sau rata de esantioanare (esantioane /secunda) sau frecventa de esantionare (Hertz).
Esantionarea periodicica existenta unei relatii între variabilele independente ale semnalului analogic si discret, adica între t si n
![]()
deci, va exista o relatie între
frecventa F (sau![]() )a semnalului analogic si f (sau
)a semnalului analogic si f (sau ![]() ) a semnalului discret. Pentru a stabili aceasta relatie, se considera un semnal
analogic de forma:
) a semnalului discret. Pentru a stabili aceasta relatie, se considera un semnal
analogic de forma:
![]()
care este esantionat periodic cu Fs=1/T esntioane pe secunda si produce semnalul:
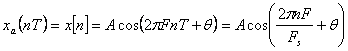
daca se compara cele doua relatii anterioare se observa ca frecventele F si f sunt legate prin relatia:
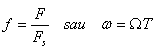
Domeniile
în care pot lua valori marimile F si ![]() pentru semnalele analogice
sunt:
pentru semnalele analogice
sunt:
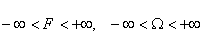
în
timp ce pentru semnalele discrete f si ![]() iau valori în domeniile:
iau valori în domeniile:
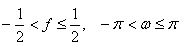
rezulta: ![]() respectiv
respectiv ![]()
În cazul esantionari în domeniul timp a unui semnal analogic se prezinta în continuare esantionarea uniforma cu memorare si naturala.
În
esantionarea ideala, modelul de extragere a unui esantion din
semnal consta în înmultirea semnalului cu un impuls Dirac. Daca
se considera cazul esantionarii uniforme, cu pasul de
esantionare T=1/Fs, modelul esantionarii ideale se
extinde la înmultirea semnalului analogic cu semnalul periodic ![]() , care este distributia
Dirac periodica. În figura 1a. se prezinta un semnal analogic
esantionat uniform, iar modelul matematic al esantionarii uniforme
este prezentata în figura 1b.
, care este distributia
Dirac periodica. În figura 1a. se prezinta un semnal analogic
esantionat uniform, iar modelul matematic al esantionarii uniforme
este prezentata în figura 1b.

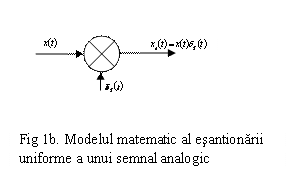
Conform modelului, semnalul esantionat xs(t) are expresia:
![]()
din xs(t) se extrag valorile semnalului la momentele de timp ce ssunt multipli de T, la restul momentelor fiind zero. Aceste valori vor reprezenta esantioanele semnalului discret.
În sistemele de transmisie a
informatiei care utilizeaza modulatia impulsurilor în
amplitudine se utilizeaza o esantionare cu memorare.
Dupa obtinerea esantionului xa(nT) se genereaza
un impuls cu amplitudinea egala cu valoarea esantionului si
durata ![]() . Semnalul esantionat xsm(t)
se prezinta sub forma unui tren de impulsuri, cu perioada de
repetitie T, modulat, în amplitudine cu valorile semnalului xa(t)
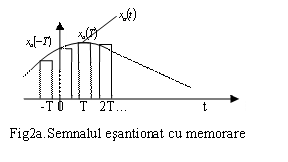
la momentele de timp nT. În figura 2a. se prezinta un semnal
esantionat cu memorare pe durata
. Semnalul esantionat xsm(t)
se prezinta sub forma unui tren de impulsuri, cu perioada de
repetitie T, modulat, în amplitudine cu valorile semnalului xa(t)
la momentele de timp nT. În figura 2a. se prezinta un semnal
esantionat cu memorare pe durata ![]() , iar în figura 2b. modelul
matematic al esantionarii cu memorare.
, iar în figura 2b. modelul
matematic al esantionarii cu memorare.
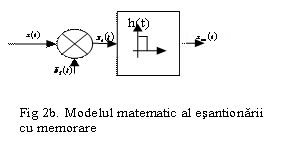
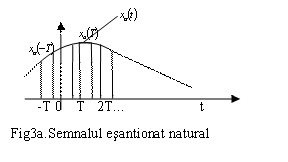
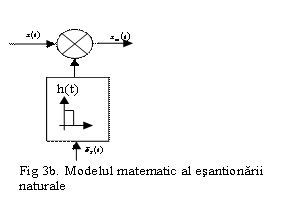
Esantionarea naturala sau
cu
urmarire corespunde operatiei de retinere a unor
portiuni din semnalul de durata ![]() si distantate între ele cu T. în
figura 3a. este prezentata un semnal esantionat natural xsn(t)
iar în figura 3b.modelul mathematic al esantionarii naturale, care corespunde
înmultirii semnalului cu un tren de impulsuri de amplitudine unitara,
durata
si distantate între ele cu T. în
figura 3a. este prezentata un semnal esantionat natural xsn(t)
iar în figura 3b.modelul mathematic al esantionarii naturale, care corespunde
înmultirii semnalului cu un tren de impulsuri de amplitudine unitara,
durata ![]() si interval de repetitie T.
si interval de repetitie T.
În aceasta lucrare se urmareste ilustrarea a doua notiuni de baza în procesul de esantionare: eroarea de alias si reconstructia semnalului.
Spectrul semnalului esantionat ideal
Fie xa(t) un semnal analogic aperiodic de energie finita, al carui spectru este:
![]()
Semnalul xa(t) poate fi refacut din spectrul sau prin transformata Fourier inversa:
![]()
Se observa ca pentru refacerea semnalului sunt necesare componentele de frecventa dintr-un domeniu infinit.
Spectrul semnalului esantionat x[n] se calculeaza cu relatia:
![]()
sau:
![]()
Semnalul x[n] poate fi refacut
din spectrul X(![]() ) sau X(f) prin
transformarea inversa:
) sau X(f) prin
transformarea inversa:
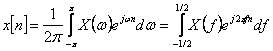
Pentru determinarea relatiei dintre spectrul semnalului analogic si al semnalului esntionat se foloseste urmatoarea relatie dintre variabilele independente t si n ale semnalelor xa(t) si x[n], adica:
t-nT-n/Fs
se obtine:
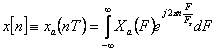
si
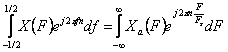
Esantionarea periodica implica o relatie între frecventele F si f corespunzatoare semnalului analogic si esantionat de forma:
f=F/Fs, unde Fs este frecventa de esantionare.
Rezulta relatia:
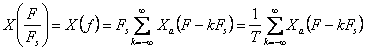
Aceasta relatie reprezinta legatura dintre spectrul X(f) a semnalului esantionat si spectrul Xa(F) al semnalului analogic. Spectrul semnalului esantionat este suma reprezentarilor periodice, cu perioada Fs, aspectrului semnalului anlogic scalat cu Fs.
Teorema esantionarii
Pentru a se putea stabili perioada de esantionare T, sau echivalent, frecventa de esantionare Fs optima pentru refacerea semnalului analogic din cel esantionat, trebuie cunoscuta frecventa cea mai înalta din spectrul semnalului analogic. În multe cazuri acest lucru este posibil. Uneori însa nu se cunosc astfel de detalii despre semnal (valoarea maxima a frecventei), scopul prelucrarii fiind chiar obtinerea acestora.
Daca semnalul analogic xa(t) este de banda limitata, adica Xa(F)=0 pentru |F|>B, atunci xa(t) este unic determinat de multimea esantioanelor sale , frecventa de esantionare este Fs≥2Fmax=2B. Semnalul initial poate fi reconstituit utilizand o relatie de interpolare.
Un exemplu de functie de interpolare ideala este:
![]() ,
,
caz în care semnalul analogic xa(t) este dat de relatia:
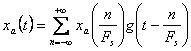 , unde
, unde 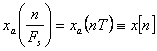 sunt esantioanele lui
sunt esantioanele lui ![]() .
.
Frecventa de esantionare FN=2B=2Fmax poarta numele de frecventa Nyquist.
Realatia anterioara poarta
numele de formula de interpolare
ideala pentru reconstructia semnalului analogic ![]() din esantioanele sale. Se
observa ca în fiecare punct de esantionare la formarea
semnalului contribuie o singura functie de interpolare. În intervalul
dintre doua esantionari, la formarea semnalului contribuie toate
functiile de interpolare.
din esantioanele sale. Se
observa ca în fiecare punct de esantionare la formarea
semnalului contribuie o singura functie de interpolare. În intervalul
dintre doua esantionari, la formarea semnalului contribuie toate
functiile de interpolare.
Daca frecventa de esantionare este mai mica decat frecventa Nyquist apar erori datorate fenomenului de aliere a lobilor spectrali vecini. (eroarea alias sau fenomenul de aliere)
Eroarea de alias determinata de esantionare.
Deoarece în MATLAB nu este posibil a avea un semnal analogic, trebuie simulata axa t a timpului real (caracteristic semnalelor analogice).
Eroarea alias a unui semnal sinusoidal.
Fie semnalul analogic sinusoidal:
![]()
pe care îl esantionam la Fs=1/Ts, pentru a obtine semnalul în timp discret:
![]()
Prezenta erorii alias ilustrata daca se reprezinta x n pentru diferite combinatii între F0 si Fs. Programul P5_1 ilustreaza procesul de esantionare:
Exercitiul 1 ( P5_1 ):
Pentru semnalul esantionat dat de relatia (1.2), fie Fs=8 kHz.
a)
Sa se reprezinte cu stem
semnalul sinusoidal esantionat. Frecventa semnalului sinusoidal este
F0=300 Hz si esantioanele luate de la 0 ms la 10 ms.
Faza ![]() este
arbitrara.
este
arbitrara.
b) Sa se reprezinte semnalul discret cu plot. În acest caz punctele sunt conectate cu linii, astfel încât alura sinusoidala este evidenta. Conectarea punctelor cu linii este o forma de reconstructie a semnalului care transforma semnalul discret în semnal continuu. Aceasta nu este forma ideala data de termenii esantionarii, dar, în multe situatii este satisfacatoare.
c) Sa se efectueze mai multe reprezentari ale semnalului discret, modificând F0 de la 100 Hz la 475 Hz în pasi de 125 Hz. Folositi subplot pentru reprezentare. Comentati.
d) Repetati c) dar variati frecventa sinusoidei de la 7525 la 7900 Hz în pasi de 125 Hz. Comentati fenomenul în comparatie cu punctul c).
e) Refaceti c) dar variati frecventa F0 de la 32100 la 32475 în pasi de 125 Hz. Anticipati forma semnalului în timp ce mariti sau micsorati frecventa sinusoidei.
Esantionarea vazuta în domeniul frecventa
Prin esantionarea unui semnal continuu, spectru sau poate prezenta fenomenul de alias datorita repetarii periodice cu frecventa de esantionare a spectrului semnalului initial. Pentru a observa acest fenomen în realitate este nevoie de un osciloscop. In MATLAB poate fi doar simulat efectul esantionarii, acesta fiind un dezavantaj al laboratorului.
Simularea consta în esantionare, urmata de conversia D/A ce include un filtru de reconstituire. Acestui sistem i se va aplica un semnal sinusoidal cu diferite frecvente si sunt comparate transformatele Fourier ale semnalelor analogice si discrete.
Pentru a simula semnale analogice se va folosi o viteza de esantionare foarte ridicata, de cel putin 5 ori, cea mai înalta frecventa pe care o are semnalul.
În concluzie, vor exista doua viteze de esantionare în aceasta problema: una pentru esantionare si una pentru simularea semnalului continuu mult mai mare decât cea de esantionare. O a doua problema este aceea de reprezentare a transformatei Fourier a semnalului analogic. Acesta poate fi numai simulat. Urmatorul program MATLAB poate fi folosit pentru reprezentarea spectrului analogic. Una din marimile de intrare este dt pentru simulare. Astfel se va alege ca frecventa de simulare o frecventa de cel putin 5 ori mai mare decât frecventa de esantionare (în cazul aplicatiilor Fsim se va lua de 10 ori mai mare decât Fs).
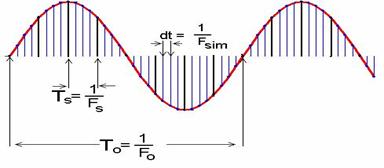
Exercitiul 2( P5_2 ): Generarea semnalului
se va folosi, pentru început, un semnal sinusoidal. Frecventa de simulare se considera a fi fsim=80 kHz.
a) Sa se genereze un semnal simulat analogic:
x(t)= cos(2pf0t+f 0 t T
Faza se considera aleatorie. Sa se genereze esantioanele (la frecventa fsim) în intervalul de lungime T. Sa se aleaga T astfel încât sa se obtina aproximativ 900-1000 esantioane ale semnalului analogic simulat.
b) Vizualizati semnalul cu plot, astfel încât esantioanele sa fie unite.
c) Sa se reprezinte transformata Fourier a acestui semnal cu functia fft.
Reconstructia semnalelor din esantioane
Procesarea digitala a semnalelor implica, printre altele, reconstructia semnalelor analogice din esantioane. În continuare sunt investigate diverse metode ce pot fi folosite pentru a reconstrui semnalul analogic din care provin esantioanele. Deoarece exista multe semnale analogice posibile care pot avea esantioanele date, alegerea semnalului analogic depinde de ipotezele ce se fac asupra reconstructiei. Fie cazul considerat în Fig.1, în care sunt prevazute trei esantioane ale unui semnal analogic x(t):
x(0)=2, x(1)=1, x(2)=x(t) t=2
fara alte precizari suplimentare.
Se pune problema de a afla carui semnal analogic corespund aceste esantioane. Este important de specificat ca nu exista un ,,raspuns corect" la aceasta problema. Acest lucru depinde de consideratiile asupra metodei de reconstituire. De exemplu, un posibil semnal este cel din Fig.2, dar evident se pot desena o multime de linii care sa uneasca cele 2 puncte.
Fig. 1 Fig 2
Concret, se efectueaza urmatoarele ipoteze: în exemplul considerat exista trei esantioane egal distante. Se presupune ca esantioanele sunt luate pentru toate valorile posibile ale lui n, de la - la + si numai acestea trei sunt diferite de zero. Pe de alta parte, se poate presupune ca aceste trei esantioane sunt o multime a tuturor esantioanelor posibile pentru n de la - la + , dar nu s-au dat toate cele diferite de zero, ci numai acestea trei.
În alegerea metodei de reconstituire, trebuie sa se decida daca aproximarea este polinomiala, cu functii sinusoidale, interpolare ideala, filtru trece-jos sau orice alta metoda. În continuare se va urmari aproximarea cu o functie sinusoidala, polinomiala si apoi cu filtrare trece-jos neideala.
Exercitiul 7 (teoretic):
Presupunem ca cele trei esantioane corespund unei functii sinusoidale
x(t)=Acos(wt+f
pentru care avem x(0),x(1),x(2). Este suficient pentru a determina A, w si f? Pot fi acestea rezolvate întotdeauna? Daca nu, dati valori particulare pentru care demersul esueaza.
Puteti intui raspunsul corect? Având raspunsul corect, gasiti un alt raspuns pentru o frecventa diferita w. Reprezentati sinusoidele rezultate folosind un grid foarte fin mai mic de Dt=0.01 s.
Exercitiul 8( P5_8 ): Interpolare liniara si polinomiala
a) Folosind MATLAB, conectati esantioanele cu linii drepte. Reprezentati rezultatul cu un grid Dt=0.01 s.
b) Efectuati convolutia celor trei esantioane cu un raspuns la impuls care este triunghiular, dar înainte inserati câte 4 zerouri între esantioane si folositi raspunsul la impuls. . Aratati ca acest rezultat este identic cu interpolarea liniara daca presupunem ca esantioanele la t=-1 si t=3 sunt zero.
c) Folosind MATLAB, aproximati semnalul analogic cu un polinom de gradul al 2-lea (polyfit, polyval). Reprezentati polinomul cu un grid fin pentru -5<t<5. Este aceasta cerinta realista în sens practic? Are sens extinderea domeniului semnalului în afara domeniului 0<t<2? Periodizati secventa si încercati sa aproximati semnalul analogic cu un polinom de gradul 10 .Ce observati?
Exercitiul 1
Fo=300;
Fs=8000;
tfinal=10*10^-3;
tn=0:1/Fs:tfinal-1/Fs; %ms
phi=0;
x=sin(2*pi*Fo*tn+phi);
subplot(211);stem(10^3*tn,x);
ylabel('Amplitude');
title('Semnalul esantionat x_(t)');
axis([0 10 -1.2 1.2])
subplot(212);plot(10^3*tn,x);
%xlabel('Time, msec');
ylabel('Amplitude');xlabel('Time, msec');
title('Semnalul continuu x_(t)');
axis([0 10 -1.2 1.2])
Exercitiu 2
N=499;
Fsim=80000;
Fo=300;
Fs=8000;
%a)
xa=cos(2*pi*(Fo/Fsim)*(0:N)+phi);
%b)
xs=[];
xn=[];
for i=1:length(xa)/(Fsim/Fs);
xn(i)=xa(1+(Fsim/Fs)*(i-1));
xs=[xs 1 zeros(1,(Fsim/Fs)-1)];
end;
figure(1);title('Semnalele din conversia A/D');
subplot(511);plot((0:length(xa)-1),xa);axis([0 (length(xa)-1) -1.2 1.2 ]);
legend('Continuu');
subplot(512);stem((0:length(xs)-1),xs);axis([0 (length(xs)-1) -1.2 1.2]);
legend('Semnalul folosit la esantionare');
subplot(513);stem((0:length(xn)-1),xn);axis([0 (length(xn)-1) -1.2 1.2]);
legend('Semnalul esantionat');
subplot(514);plot((0:length(xn)-1),xn);axis([0 (length(xn)-1) -1.2 1.2]);
legend('Semnalul esantionat scris cu plot');xlabel('timp');
P5_8
figure
x=[2 1 -1];
n=[0 1 2];
subplot(2, 1, 1);plot(n,x);grid
%b)
x1=[2 0 0 0 0 1 0 0 0 0 -1 0 0 0 0];
h=[0.2 0.4 0.6 0.8 1.0 0.8 0.6 0.4 0.2];
xr=conv(x1,h);
%c)
n=0:length(x1)-1;
p=polyfit(n,x1,2);
xr1=polyval(p,n);
subplot(212);plot((0:2/length(xr1):2-2/length(xr1)),xr1);grid
|