SURSE DE CURENT

tehnica mecanica

  R­_e ≈ (R_Bech+h_11e) / (R_Bechh_22e+Dh_e)

cu :

-Dh_e=h_11eh_22e-h_12eh_21e - determinantul matricii cu

parametri h_e

-valorile tipice ale parametrilor h_e de la curenti

mici, de exemplu la 20mA, sunt : h­_11e=200 kW

h_21e=200; h_12e=10^-5; h_22e= 0,2·10^-6 S ;

rezulta: Dh_e= h­_11eh_22e = 0,04

Deci la curenti de colector mici:

R­_e=(R_Bech+h_11e) / (R_Bechh_22e+ h­_11eh_22e) = 1/h_22e ≈ 5 MΩ

Desigur, este posibila si folosirea parametrilor " r ". Intre acestia si parametrii h se considera relatiile de legatura

r_e≈h_11e , β≈ h_21e si r_c sau r_o≈1/ h_22e

si rezulta o valoare egala aproximativ cu r_o.

Cazul 2. Rezistenta de iesire a unui tranzistor cu rezistenta în emitor.

Dh_e)] =

= (R_Bech+h_11e+h_21eR_E) / (R_Bech+R_E+h₁₁)h_22e

(deoarece ∆h_e = h­_11eh_22e ),

care este mai mare decât în cazul 1 datorita

termenului h_21eR_E .

Obs: când R_E devine mare

R_e h_21eR_E/h_22eR_E = h_21e/h_22e = h_21e (1/h_22e)

deci este de h_21e ori mai mare decât în cazul 1. Se vede astfel mecanismul de crestere a rezistentei de iesire.

Calculul rezistentei de iesire a sursei de curent simple, cel mai frecvent utilizata în circuitele integrate.

Circuitul este asemanator cu cel din cazul 1 deci

R_e=1/h_22e

: Cu aceasta ocazie se reaminteste valoarea rezistentei dinamice a unei diode realizata cu tranzistor (motivul folosirii tranzistorului drept dioda este : compensarea termica pentru efectele lui U_BE dar si b, ceea ce o dioda simpla - o jonctiune emitoare - nu asigura ! ). Se calculeaza pentru aceasta :

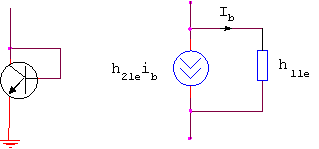
r_d = u_d/i_d = i_bh_11e/(h_21e+1)i_b h_11e/h_21e

care, la curent de ordinul 20 μA este de cca 1 kΩ.

Circuitul se încadreaza în cazul 2. Se considera parametri tranzistoarelor apropiati, pentru simplicitate.

R_e = (R_Bech+h_11e+h_21eR_E) / (R_Bech+R_E+h₁₁)h_22e

Aici R_Bech= R_B h_11e/ h_21e h_11e/ h_21e

deci :

Numeric, pentru un curent de 20 μA si R_E = 1 kΩ, se obtine R_e = 10 MΩ.

Calculul rezistentei de iesire a sursei ,,cascoda".

Circuitul se utilizeaza deoarece permite obtinerea unei rezistente R_e1 de valoare mare, întrucât T1 are în emitor o rezistenta R_E=R_e2=mare (dar care nu ocupa loc mult pe placheta - ca un R_E), de valoare mare.

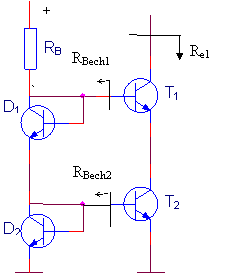Se considera tranzistoarele la acelasi curent. Se poate trata ca si în cazul 2 pentru ca reactia din baza lui T₂ si prin diodele D₁,D₂ este foarte slaba. Circuitul simplificat are forma :

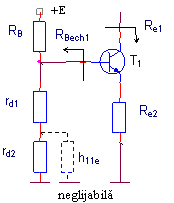
Pentru acestadeoarece, în baza diodei D₂ se vede rezistenta

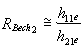
Pe circuitul simplificat

adica, o valoare foarte mare , scontata, asa cum s-a aratat la problema 1.2, pentru R_E de valoare foarte mare.

La curenti mai mari R_e1 este mai mica.

Calculul rezistentei de iesire a oglinzii Wilson (varianta 1)

Deoarece schema include o reactie negativa serie-paralel nu se mai poate determina rezistenta de iesire printr-o formula stabilita simplu, ca la alte oglinzi. Aici se va utiliza o metoda de calcul bazata pe teoria reactiei negative de la amplificatoare. Într-adevar, circuitul se poate considera ca un amplificator cu intrarea pe borna de alimentare a ramurii de referinta.

Desenarea circuitului "A" se face stiind ca circuitul A include etajul amplificator cu T₁ , la care se adauga:

rezistenta de sarcina mutata pe firul de legatura astfel încât la iesirea circuitului A sa se realizeze sarcina ideala pentru configuratia bucla : scurtcircuitul.

rezistenta R_B a sursei de semnal, mutata în paralel cu intrarea , dupa transfigurarea sursei de tensiune în sursa de curent (cu teorema lui Norton).

parte din circuitul de reactie, la iesirea circuitului A, prin scurtcircuitarea la masa a nodului de la intrare.

parte din circuitul de reactie, la intrarea circuitului A, prin întreruperea buclei de iesire (în emitorul lui T₁).

Astfel va rezulta circuitul 

Deoarece T₂ intervine în paralel cu h_11e/ h_21e (T₃) prin rezistenta sa de intrare mult mai mare - h_11e2 se poate neglija în circuitul din emitorul lui T₁.

Pentru calculul marimii A pe circuitul "A" se va face o aproximare prin neglijarea în modelul "h" al tranzistorului T₁ a rezistentei din circuitul de iesire. Atunci i_e h_21ei_b1 . Marimea A este aici o amplificare de curent . Notând

rezistentele în circuitul de intrare, avem:

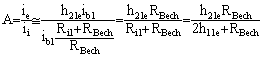
unde s-a folosit divizarea de curent în circuitul de intrare pentru a-l înlocui pe i_i în functie de i_b1 si s-a calculat rezistenta de intrare a lui T₁ cu relatia cunoscuta:

f)     

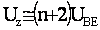
Neglijând I_oR₁ rezulta:

si luând pe U_z de exemplu 4,0V

Observatie : Aici avem nevoie de fapt de un tabel cu K_TUz , dat în functie de U_z , pentru a stabili corect numarul final de diode.

1.14 Pentru sursa de curent multipla din figura, alimentata cu tensiunea variabila U, se cer :

a) Sa se calculeze la 300K curentii de iesire I_C11 si I_C14 ai sursei si sa se verifice ca acestia nu depind de tensiunea de almentare U. Aria jonctiunii emitoare a lui T₁₀ este de 10 ori mai mare decât aceea a lui T₁₂ (asa cum arata cifrele înscrise lânga emitoarele acestor tranzistoare). Curentii de baza se neglijeaza.

b) Sa se calculeze rezistenta R₁ pentru care I_C10≈I_C11.

Observatie : Circuitul face parte din integratul « senzor de temperatura » βM335.

Solutie

a) Neglijând curentii de baza ai tranzistoarelor se poate scrie pe bucla ce include cele patru jonctiuni emitoare ale tranzistoarelor T₁₀.T₁₃ :

I_C13R₂=-U_BE13-U_BE10+U_BE11+U_BE12=

(deoarece I_Co este proportional cu aria jonctiunii emitoare iar la tranzistoarele nemarcate lânga emitor, se considera tot cifra 1 în raportul ariilor). Având însa

I_C11=I_C13 rezulta U_BE11=U_BE13 si

I_C10=I_C12 dar U_BE10≠U_BE12

se obtine

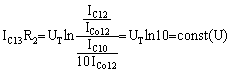
Deci

Cum la sursa de curent « standard » formata din T₁₃ si T₁₄ împreuna cu rezisten-tele din emitoarele lor avem :

rezulta   

b) Rezulta din legea lui Ohm :