UNDE ACUSTICE sI UNDE SONORE

Biofizica - Conf. Dr. Constanta GANEA - Curs 8.2

UNDE ACUSTICE sI UNDE SONORE

Perturbatiile mediului aerian, produse de cauze diverse, se propaga în mediul pe care-l strabat sub forma unor variatii de presiune. Aceste fluctuatii de presiune constituie undele acustice. Pentru anu 242s1820c mite valori ale frecventelor i presiunilor, undele acustice pot fi detectate de urechea umana sub forma sunetelor. Intervalul de frecvente la care este sensibila urechea umana este situat între aproximativ 16 - 20.000 Hz, iar undele acustice situate în acest domeniu se numesc si unde sonore. Uneori, termenul de unda sonora este utilizat în mod incorect si pentru undele acustice situate în afara intervalului de audibilitate la om. Undele acustice cu frecvente mai mici de 16 Hz se numesc infrasunete, iar cele cu frecvente mai mari de 20.000 Hz se numesc ultrasunete.

Desi termenul de sunet este corelat cu aspectul subiectiv al fenomenului acustic, el se utilizeaza în mod curent si atunci când se fac referiri la fenomenul fizic obiectiv, respectiv la undele acustice din domeniul de frecvente 16 - 20.000 Hz.

Cele mai simple unde acustice sunt undele sinusoidale de frecvente, amplitudini si lungimi de unda definite. Când astfel de unde din domeniul undelor sonore ajung la ureche, ele provoaca vibratia particulelor de aer din apropierea timpanului si dau nastere unui sunet daca presiunea este mai mare de 20 mPa (limita de audibilitate sau pragul auzului) si mai mica de 20 Pa (pragul dureros).

Viteza undei longitudinale

Viteza de propagare a unui puls longitudinal într-un fluid depinde numai de modulul de compresibilitate B si de densitatea fluidului r

Considerând, în cazul undelor acustice, procesele adiabatice:

B_ad = gp

Viteza undei, c, în cazul gazului ideal devine:

si este cunoscuta sub numele de formula Laplace. Expresia anetrioara poate fi rescrisa în functie de temperatura. Pentru un gaz ideal :, în care R este constanta gazului ideal, T este temperatura absoluta în grade Kelvin, iar M este masa molara în Kg/Kmol. Expresia vitezei undei pentru gazul ideal, în functie de temperatura, va fi:

Dar g, R si M sunt constante pentru un gaz ideal dat:

Daca se foloseste aceasta formula pentru a calcula viteza undelor longitudinale în aer, se obtine, înlocuind M = 28,8 Kg/Kmol, g= 1,4 si R = 8,31 10³ J/KmolK, pentru temperatura de 300 K (27⁰C):

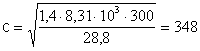m/s.

Acest rezultat obtinut pe cale teoretica concorda cu o eroare de pâna la 0,3% cu viteza masurata experimental la aceasta temperatura.

Presiune instantanee, presiune de vârf si presiune eficace

Presiunea acustica p(t) este o marime variabila; valoarea ei la un moment dat este numita presiune instantanee. Valoarea maxima a presiunii instantanee în intervalul de timp considerat se numeste presiune de vârf.

Presiunea eficace este:

Impedanta acustica

Notiunea de impedanta este întâlnita în diferite domenii ale fizicii, fiind definita, în general, ca raportul dintre o marime "activa", cum ar fi forta, presiunea sau tensiunea electrica si o marime "reactiva" cum ar fi viteza sau intensitatea curentului electric. De exemplu, într-un circuit de curent alternativ, conform legii lui Ohm:

unde:

Z - impedanta electrica

U - tensiunea electrica

I - intensitatea curentului electric

Impedanta reprezinta, deci, capacitatea unui sistem de a se opune actiunii marimii active.

Impedanta acustica, notata ca si impedanta electrica cu Z, este egala cu raportul dintre presiunea si viteza acustica:

Impedanta acustica se masoara în sistemul SI în Rayl (denumire data în onoarea lordului Rayleigh) sau Ohmi acustici.

1 Rayl (1 Ohm acustic) = 1 Kg m^-2s^-1.

Expresia impedantei acustice poate fi scrisa sub o alta forma, în functie de viteza undei si de densitatea mediului:

, unde si deci:

În conditii de presiune si temperatura bine determinate, impedanta unui mediu de densitate r se numeste impedanta caracteristica si este notata cu Z₀ :

Impedanta caracteristica a aerului la temperatura de 22⁰C si presiunea atmosferica de 1 bar (1,013 10⁵Pa) se calculeaza tinând cont de faptul ca viteza undei acustice este în aceste conditii 340 m/s, iar densitatea aerului r =1,206 Kg/m³:

1,2 340= 410 Kg m^-2 s^-1 = 410 Rayl (Ohmi acustici)

S-a normalizat aceasta valoare la 400 Ohmi acustici.

Pentru apa: Kg/m³,   c = 1410 m/s, Z_c=1,48 MOhmi acustici.

Intensitatea acustica

Intensitatea I a unei unde acustice reprezinta energia acustica transportata de unda, în unitatea de timp, prin unitatea de suprafata perpendiculara pe directia de propagare. Cu alte cuvinte, intensitatea este puterea medie transportata prin unitatea de suprafata. Se stie ca puterea dezvoltata de o forta F este egala cu produsul dintre forta si viteza: . Într-un punct al spatiului, la un moment dat, intensitatea instantanee i va fi data de raportul dintre puterea P si suprafata S:

, unde p_i si v_i sunt, respectiv, presiunea si viteza acustica instantanee. Intensitatea instantanee se masoara în Watt/m². Prin definitie, intensitatea este valoarea medie a intensitatii instantanee.

În cazul în care viteza si presiunea acustica sunt în faza . Folosind expresia impedantei acustice si înlocuind viteza acustica în expresia intensitatii, se obtine :

Între intensitatea acustica si impedanta acustica exista o relatie de proportionalitate inversa. Faptul ca intensitatea este proportionala cu patratul amplitudinii marimii ondulatorii considerate este o caracteristica a tuturor tipurilor de miscare ondulatorie. Intensitatea unei surse sonore având amplitudinea minima perceptibila de catre urechea umana poate fi calculata cu aceasta formula, considerând impedanta acustica a aerului, Z, aproximativ egala cu 400 Ohmi acustici. Presiunea prag este de 20 mPa:

W/m²

Deci, intensitatea pragului normal de audibilitate este 10^-12W/m² = 1 pW/m².

Puterea acustica

Puterea acustica a unei surse sonore este cantitatea de energie acustica emisa de sursa sau transportata de catre un fascicul sonor în unitatea de timp, în directia de propagare a undei. Puterea totala transportata printr-o suprafata de catre o unda sonora este egala cu produsul dintre intensitatea undei pe acea suprafata si aria suprafetei, daca intensitatea este uniforma pe suprafata:

Puterea acustica (sau fluxul acustic) se masoara în Watt.

Puterea medie dezvoltata sub forma de unde sonore de catre o persoana care vorbeste pe un ton obisnuit de conversatie este de cca. 10^-5 W.

NIVELE ACUSTICE. SCǍRI DE DECIBELI

Notiuni introductive privind marimile în decibeli

Numeroase domenii ale tehnicii utilizeaza notatia în decibeli, în scopul simplificarii expresiilor unor marimi care au valori într-un interval care acopera mai multe ordine de marime. Scarile de decibeli sunt scari logaritmice de evaluari relative, care exprima raportul a doua marimi de acelasi tip. Un asemenea raport este un numar adimensional. Pentru a exprima în decibeli o marime M, în cazul în care aceasta marime este o putere (putere acustica, putere electrica, etc.), se utilizeaza relatia:

reprezinta marimea exprimata în decibeli (dB);este valoarea de referinta a marimii respective, care se exprima în unitatile de masura adecvate; este marimea care trebuie transformata, exprimata în aceleasi unitati ca si . O alta unitate de evaluare relativa este Bel-ul (B), astfel încât:

si

Pentru exprimarea în decibeli a altor marimi, cum ar fi presiunea acustica, intensitatea sau tensiunea electrica, se folosesc relatiile dintre aceste marimi si puteri, asa cum se va vedea mai departe în cazul presiunii acustice.

Nivele acustice

În acustica, datorita faptului ca urechea este sensibila la un interval foarte mare de intensitati, respectiv presiuni acustice, scara logaritmica este mai comod de utilizat decât scara lineara. Astfel, intensitatea pragului normal de audibilitate este I₀=10^-12 W/m², iar pragul dureros se afla în jurul valorii de 1 W/m². Intervalul de valori în care se situeaza intensitatile sonore care pot fi percepute de ureche cuprinde, astfel, 12 ordine de marime. De asemenea, presiunile sonore variaza între 20 mPa si 20 Pa, reprezentând un interval care cuprinde 6 ordine de marime. De aceea, efectuarea calculelor de marimi acustice în valori absolute si, de asemenea, reprezentarea grafica a acestor marimi, ar prezenta o serie de dificultati si inconveniente. Marimile acustice care se exprima în mod curent în decibeli sunt: intensitatea, presiunea si puterea acustica. Relatiile de transformare corespunzatoare sunt:

Intensitatea acustica:

cu valoarea de referinta : I₀ =10^-12 W/m² = 1 pW/m².

Presiunea acustica: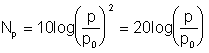

cu valoarea de referinta: p₀ = 2 mPa.

Puterea acustica:

cu valoarea de referinta: P₀ = 10^-12 W = 1 pW.

Pentru nivelele de intensitate si presiune, valorile de referinta corespund valorilor pragului normal de audibilitate la frecventa de 1.000 Hz. Nivelul de intensitate acustica si cel de presiune acustica sunt exprimate printr-un acelasi numar. Ele sunt caracteristice unui punct al câmpului. Se constata cu usurinta ca între cele 2 nivele exista o relatie strânsa, asa cum s-a aratat la începutul acestui paragraf. Folosind expresia intensitatii: , se poate deduce relatia:

Acest lucru este posibil datorita faptului ca în ambele cazuri s-a luat aceeasi valoare de referinta si anume cea corespunzatoare pragului normal de audibilitate. De aceea, cunoasterea uneia dintre cele doua marimi implica cunoasterea celeilalte, fara calcule suplimentare.

Pentru decibelii acustici se mai foloseste si notatia dBSPL, notatie care arata ca este vorba de decibeli pentru nivelul de presiune sonora (SPL -sound pressure level). Aceasta precizare se face pentru a evita eventualele confuzii cu alte scari de decibeli care se folosesc în audiometrie. Tabelul prezinta câteva nivele de intensitate sonora în dB ale unui numar de zgomote obisnuite.

Analiza Fourier

În cazul mediilor lineare, orice vibratie complexa poate fi obtinuta prin suprapunerea unor vibratii sinusoidale având diferite frecvente, amplitudini si faze. Pentru a afla compozitia unei vibratii complexe se utilizeaza tehnicile de analiza spectrala. Un spectru al unei marimi (de exemplu, intensitate, putere, nivel etc.) reprezinta totalitatea componentelor acelei marimi în functie de una dintre caracteristicile miscarii vibratorii (frecventa, perioada, lungime de unda). În optica, de exemplu, daca se reprezinta intensitatea luminoasa în functie de lungimea de unda, în urma trecerii unui fascicol luminos printr-o solutie, se obtine un spectru de absorbtie al acelei substante.

Matematicianul Fourier (1768-1830) a aratat ca o functie f(t) continua si periodica, nesinusoidala, poate fi descompusa într-o serie de termeni, primul constant si ceilalti sinusoidali. Fiecare termen sinusoidal, numit armonica si având frecventele ..., n , respectiv pulsatiile ,..., n , este caracterizat printr-o amplitudine si o faza determinate:

Primul termen este numit armonica 1-a sau fundamentala, termenul al doilea este numit armonica a 2-a s.a.m.d.

Coeficientii diferitilor termeni se calculeaza prin integrare, aplicând integralele Fourier. Determinarea armonicelor unei functii f(t) reprezinta analiza Fourier a acelei functii. Se poate spune ca o armonica este o unda a carei frecventa este un multiplu întreg al unei frecvente minime numita fundamentala. Des­com­punerea într-o serie Fourier este reprezentata grafic în functie de frecventa si se obtine în acest fel o reprezentare spectrala. Astfel, un acelasi fenomen vibratoriu poate fi reprezentat temporal sau spectral.