Starea de saturatie a rocilor

Starea de saturatie a rocilor

14.1. Definitii si generalitati

Rocile de zacamânt, dar si mediile poroase în general, contin diverse fluide. Porii rocii sunt în întregime ocupati cu una sau mai multe faze, cu rare exceptii când, în conditii de laborator, probele de carota sunt vidate. Masura si modul în care fluidele ocupa porii rocii reprezinta starea de saturatie*. Se disting doua moduri de abordare a acestui concept.

Primul, de refera la masura în care fiecare din fluidele existente în roca participa la ocuparea volumului de pori. Volumul de pori se poate referi la carote, la zacaminte, la parti din zacaminte etc. Privita astfel, starea de saturatie reprezinta un parametru global si constituie o medie pentru volumul considerat. Daca acest volum este divizat în mai multe parti, fiecare parte poate fi caracterizata de o alta stare de saturatie, care reprezinta, de asemenea, un parametru global pentru volumul în cauza. În mod obisnuit, în felul acesta se defineste starea de saturatie la scara macroscopica.

Cel de al doilea mod de abordare are în vedere modul în care fazele fluide sunt dispuse în pori, mai precis, locul pe care îl ocupa fluidele în porii individuali sau în grupurile de pori vecini. Aceasta este starea de saturatie la scara micro. Între cele doua exista, asa cum se va vedea mai departe o anumita legatura, fara a exista o dependenta stricta. În cele ce urmeaza vor fi discutate, pe rând, cele doua aspecte ale starii de saturatie.

14.2. Starea de saturatie la scara macro

Cuantificarea participarii fazelor fluide la "umplerea" porilor se face prin volumul fiecarei faze raportat la volumul de pori comunicanti. Se definesc coeficientii de saturatie, S_i , pentru fiecare faza prezenta în porii rocii, cu relatia:

(14.1.)

în care Vi reprezinta volumul fazei " i" iarV_p - volumul de pori comunicanti.

Multimea coeficientilor de saturatie reprezinta starea se saturatie a rocii la scara macro. În mod curent, pentru simplificarea si fluenta exprimarii, în

*Trebuie evitata similitudinea cu saturatia unei solutii, a unui titei etc.

locul termenului de coeficient de saturatie se foloseste termenul de saturatie (la fel ca în cazul coeficientilor de porozitate, de permeabilitate etc.). Spre exemplu, se defineste saturatia în apa a unei roci, S_a, prin relatia:

(14.2.)

Este lesne de observat ca saturatiile sunt marimi pozitive subunitare:

(14.3.)

iar legea de bilant a volumelor se scrie astfel:

(14.4.)

O modalitate obisnuita de a scrie valorile saturatiilor este sub forma procentuala. Spre exemplu, în loc de a scrie S_a = 0,25, se scrie S_a = 25%. Este vorba, evident, de procente volumice.

Starea de saturatie joaca rolul de functie sau de variabila, dupa caz. Indiferent de situatie, reprezentarea starii de 13213w2210n saturatie are aceeasi particularitate cu reprezentarea compozitiei sistemelor cu doi si cu trei componenti (v. vol. I, p. 38 si 54). În figura 14.1. este ilustrat modul de reprezentare a starii de saturatie.

Ca aplicatie, pe reprezentarea din figura 14.1. se vor surprinde câteva din starile de saturatie din zacamintele de hidrocarburi si din carotele extrase din aceste zacaminte:

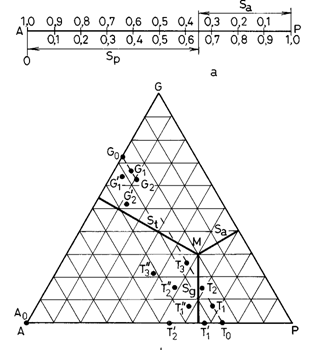
Fig. 14.1. Reprezentarea starii de saturatie.

a) sistem bifazic; b) sistem trifazic.

Tendinte de evolutie ale starii de saturatie în zacamintele de hidrocarburi.

A₀ - starea de saturatie din acviferele zacamintelor;

T₀ - starea initiala de saturatie din zacamintele de titei fara cap liber de gaze. Saturatia în apa este egala cu asa-zisa saturatie ireductibila S_a = S'_a, saturatia în titei este S_t =1 − S'_a. iar saturatia în gaze S_g = 0. Altfel scris, starea de saturatie este: . Aceasta stare de saturatie se pastreaza pâna când presiunea scade sub presiunea de saturatie. Din acest moment, saturatiile se modifica într-o maniera variata de la zacamânt la zacamânt. Spre exemplu, daca acviferul este inactiv, saturatia în apa ramâne constanta, saturatia în titei scade, iar ce în gaze creste. Punctul corespunzator starii de saturatie se deplaseaza pe o paralela la latura GT: T₀, T₁, T₂... Trebuie remarcat ca aceste puncte reprezinta starile medii de saturatie pe zacamânt. În realitate, în cuprinsul zacamântului, exista mari variatii ale starii de saturatie [84, 85]. Un caz complet diferit îl constituie zacamintele de titei cu acvifer foarte activ sau cele în care se face o injectie de apa la o scara mare, unde presiunea se mentine peste presiunea de saturatie (este un caz mai mult teoretic). În aceste zacaminte, saturatia în gaze ramâne nula, iar punctul corespunzator starii medii de saturatie de deplaseaza pe latura AT: T₀, T'₁, T'₂. Situatia cea mai frecventa este cea a zacamintelor de titei cu un acvifer care avanseaza pe masura ce presiunea de zacamânt scade. În acest caz, toate cele trei saturatii se modifica, iar punctul corespunzator se deplaseaza pe o traiectorie care poate fi anticipata, cu o anumita aproximatie, prin calcule de prevedere a exploatarii: T₀,T"₁, T"₂.

G₀ - starea initiala de saturatie din zacamintele de gaze si de gaze cu condensat. Saturatia în apa este tot saturatia ireductibila, S_a = S'_a, saturatia în gaze este S_g = 1 - S'_a, iar saturatia în condensat S_c = 0. În cazul zacamintelor de gaze fara acvifer activ. Starea de saturatie se pastreaza aproximativ constanta pe toata perioada exploatarii. Singura modificare este determinata de cresterea umiditatii odata cu scaderea presiunii (v. vol.I, p. 146) care duce la o scadere nesemnificativa a saturatiei în apa. Daca acviferul este activ, are loc o crestere a saturatiei medii în apa, iar punctul corespunzator deplaseaza pe o traiectorie predictibila prin calcule de prevedere a exploatarii [86]. În cazul zacamintelor de gaze cu condensat fara acvifer activ, starea de saturatie ramâne practic neschimbata pâna la atingerea presiunii punctului de roua, dupa care, creste saturatia în condensat si, corespunzator, scade saturatia în gaze. Dupa ce fenomenul de condensare retrograda înceteaza, satutatiile încep na se modifice în sens invers. Punctul care arata starea de saturatie se deplaseaza aproximativ pe o dreapta paralele cu latura GT cu o evolutie în timp greu, dar nu imposibil, de calculat: G₀, G₁, G₂. Daca acviferul este activ, are loc o crestere progresiva a saturatiei în apa, celelalte doua saturatii evoluând în sensul descris mai sus: la început, pâna la începerea condensarii, saturatia în condensat ramîne nula, ca apoi sa creasca si, eventual, sa scada. Traiectoria punctului de saturatie va fi G₀, G'₁, G'₂, G'₃.

Determinarea starii de 13213w2210n saturatie la scara macro are doua obiective: stabili-

rea resurselor de titei si gaze din zacaminte si evaluarea în laborator a unor proprietati ale rocilor sau simularea unor procese care au loc în zacaminte (curbe de presiune capilara, curbe de permeabilitate relativa, dezlocuirea titeiului etc. - v. capitolele urmatoare).

În principiu, metodele de determinare se împart în doua categorii: distructive si nedistructive.

Metodele distructive sunt acelea în care, în urma determinarii experimentale, starea de saturatie de modifica. Este cazul extractiei cu solvent, care consta în spalarea probei cu un solvent pâna la eliminarea completa a titeiului. Din bilantul material de afla masa si, ulterior, volumul titeiului extras, adica a celui existent la momentul initial în proba de roca. Cel mai folosit pentru extractia cu solvent este aparatul Soxtlet [18]. Odata cu extragerea titeiului are loc evaporarea si colectarea apei din proba, asa încât, dupa încheierea experimentului, proba ramâne complet saturata cu gaze.

Metodele nedistructive permit determinarea starii de 13213w2210n saturatie fara a o altereze. Acest tip de determinari este de neînlocuit în cursul urmaririi unor procese dinamice, când fluidele curg prin carota analizata (curgerea eterogena, dezlocuirea reciproca a fazelor etc.). Exista mai multe metode de acest fel, dar au un grad de complexitate ridicat. Cea mai simpla dintre ele este metoda bilantului material. Acest bilant consta în înregistrarea la anumite intervale de timp a volumelor intrate si a celor iesite. Cunoscând volumele existente la momentul initial în proba, se pot afla volumele existente la un moment dat în proba de roca si astfel se pot calcula saturatiile. Metoda presupune aparatura foarte exacta de masurare a volumelor.

Cea mai performanta metoda pentru determinarea starii de saturatie este tomografia. Prima varianta a tomografiei foloseste o sursa de raze X [38]. În ultimii ani a fost pusa la punct tomografia RMN (rezonanta magnetica nucleara), mai rapida, mai performanta si mai putin periculoasa.

În cele ce urmeaza, va fi prezentata, în linii generale, metoda tomografiei computerizate cu raze X.

Folosita mai întâi în medicina, tomografia cu raze X este o metoda de radiografiere a corpurilor opace prin care se determina densitatea si compozitia atomica. Autorul acestei metode revolutionare, Hounsfield, din Marea Britanie, a primit Premiul Nobel în anul 1979. Ulterior, metoda a fost adaptata si pentru studiul probelor de roca.

Rezultatul tomografiei este o imagine sau o succesiune de imagini color ale sectiunii transversale prin corpul studiat. "Petelor" de culoare din imaginea obtinuta le corespund elemente de volum cu proprietati distincte. Spre exemplu, daca într-o roca de precipitatie cu grad mare de omogeneitate exista o incluziune de alta natura (ex. o fosila sau un cristal de cuart) pe fondul de o anumita culoa-re a imaginii va aparea o pata de culoare diferita.

Pentru o mai buna întelegere, se prezinta mai întâi metoda conventionala

de radiografiere cu raze X (fig. 14.2.). Informatia privind atenuarea razelor X la traversarea corpului iradiat reprezinta o medie a atenuarii pe traseul de la in-trarea la iesirea din corp, asa încît contrastul de atenuare este estompat.

Legea care descrie atenuarea razelor X, scrisa de Beer are forma:

în care I₀ si I reprezinta intensitatea razei incidente si a celei care a traversat corpul cu grosimea h, iar m este coeficientul de atenuare lineara.

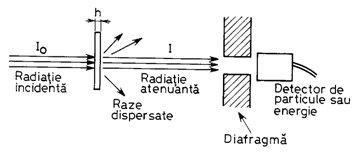
Fig. 14.2. Metoda conventionala a radiografiei cu raze X.

Coeficientul de atenuare lineara, m, depinde atât de densitatea electronica, deci si de densitatea corpului, r, cât si de numarul atomic, Z:

(14.6.)

unde a este un coeficient cvasiindependent de energie, denumit coeficientul Klein-Nishina si b este o constanta. E reprezinta energia de emisie.

Primul termen din relatia (14.6.) masoara împrastierea Compton, care este predominanta la energii mari ale razelor X (peste 100 kV) unde opereaza de regula aparatele medicale. Cel de al doilea termen al ecuatiei (14.6.) cuantifica absorbtia fotoelectrica, mai importanta la energii mai mici cu mult de 100 kV.

Prin scanarea corpului la doua nivele energetice se obtin doua imagini: una care evidentiaza densitatea corpului (la energie înalta), cealalta care evidentiaza compozitia corpului (la joasa energie).

Rezultatul scanarii este o imagine alcatuita din nxn "puncte". Un astfel de "punct" reprezinta un patrat cu latura de un pixel, cu dimensiunea în functie de rezolutia aparatului. Spre exemplu, pentru o imagine de forma unui patrat cu la-tura de 12,7 cm, alcatuita din 512x512 elemente ("puncte"), 1 pixel = 0,25 mm. Fiecarui pixel i se atribuie o nuanta de gri, de la alb pâna la negru, sau o o serie de culori, cu o paleta de nuante pentru fiecare culoare. Prin calibrare, o culoare cu nuanta respectiva reprezinta, spre exemplu, o densitate anume.

Pentru crearea imaginilor, pentru fiecare pixel se determina m din ecuatia (14.5.) care se introduce în ecuatia (14.6.), de unde se determina marimea de referinta (ex. densitatea).

În mod practic, scara intensitatii radiatiei captate de receptorul aparatului,

dupa traversarea probei, este asociata, prin calibrare, cu o paleta de culori.

Când sunt prezente mai multe specii de atomi, absorbtia fotoelectrica este proportionala cu numarul atomic efectiv, Z_e:

(14.7.)

în carer f_i este fractia de electroni a componentului i. Spre exemplu, numarul atomic efectiv al apei este de 7,4: doi electroni ai celor doi atomi de hidrogen (Z=1) si opt electroni ai oxigenului (Z=8): 2/10 1^3,8 + 8/10 8^3,8 = 7,4. Acest exemplu arata ca numarul atomic efectiv este mult mai apropiat de numarul atomic al elementului mai greu. Pe aceasta proprietate se bazeaza introducerea într-una din fazele fluide care satureaza roca a unei substante cu atomi grei, pentru a mari contrastul imaginii. Spre exemplu, iodul (Z=53) poate face parte atât din compusi solubili în titei, cât si din saruri solubile în apa.

Interpretarea atenuarii intensitatii razelor X se face prin folosirea scarii Hounsfield, cuprinsa între -1000 H (valoare corespunzatoare aerului) si 0 H (valoare corespunzatoare apei). Astfel, o unitate Hounsfield reprezinta o modificare de 1% a densitatii mediilor traversate. Pentru roci, se foloseste o scara mai extinsa, în functie de natura mineralogica. Spre exemplu, pentru gresii, termenul de referinta este cuartul topit, cu densitatea relativa de 2,2. Rezultatul unei calibrari pentru gresii este prezentat în figura 14.3.

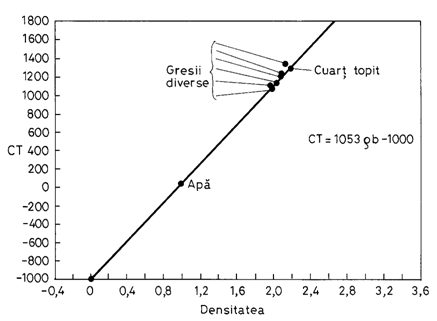
Fig. 14.3. Curba de calibrare pentru densitatea unei gresii.

Pe aceasta curba de calibrare, o modificare de 1 H este echivalenta cu o modificare Dr r de 0,5 10^-3, evident, pentru o gresie. Un procedeu similar de calibrare se aplica si pentru alte tipuri de roci supuse scanarii (calcar, dolomit etc.).

Tomografia computerizata se realizeaza astfel: sursa de raze X se roteste cu 360⁰ în jurul probei. Prin interpretarea semnalelor succesive receptate în pozitia diametral opusa sursei, se reconstiruie imaginea sectiunii transversale prin proba de roca (sau alt corp), dupa cum este aratat în figura 14.4.

Deplasând ansamblul sursa-receptor pe directie longitudinala în raport cu proba, în pasi succesivi, se obtine o succesiune de imagini ale sectiunilor transversale de-a lungul probei pentru fiecare pas (fig. 14.4. si 14.5.). Este, în fapt, o scanare a probei pe directie longitudinala.

Fig. 14.4. Principiul metodei tomografice.

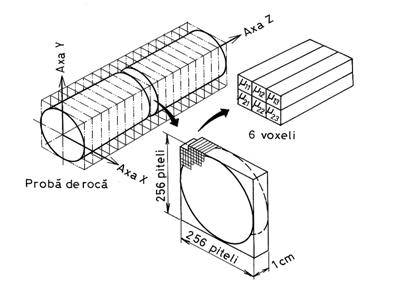
Fig 14.5. Ilustrarea modului de investigare a probelor de roca.

În felul acesta, se constituie o retea tridimensionala cu pasul de un pixel pe cele trei directii rectangulare ale unui spatiu cartezian, adica o retea cubica. Pentru fiecare nod al retelei se memoreaza o valoare de densitate, rezultata din valoarea intensitatii razei receptate.

Modul în care se acceseaza aceste data este la îndemâna operatorului. Prin sectionarea corpului cu un plan de ecuatie data se obtine sectiunea dorita. În mod curent, se realizeaza sectiuni transversale sau longitudinala cum este ilustrat în figura 14.6. Pentru fiecare plan de intersectie se obtine o imagine care reprezinta ceea ce s-ar vedea în cazul sectionarii reale a probei prin planul respectiv.

Cea mai importanta aplicatie a tomografiei computerizate cu raze X este determinarea starii de 13213w2210n saturatie, mai exact, a distributiei spatiale a starii de saturatie în probe de roca. Aceasta metoda nu altereaza în nici un fel starea de saturatie. Este, deci, prin excelenta, o metoda de determinare nedistructiva a starii de saturatie.

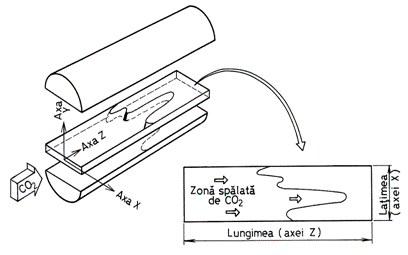
Fig. 14.6. Reconstituirea unei sectiuni longitudinale.

Când în proba sunt prezente numai doua faze, spre exemplu apa si titei, se foloseste scanarea la un singur nivel energetic. Între coeficientul de atenuare si saturatii exista relatiile:

(14.8.)

si

(14.9.)

în care m_t si m_a reprezinta coeuficientii de atenuare masurati pe aceeasi proba de roca saturata complet cu titei, respectiv cu apa. Prin rezolvarea sistemului de ecuatii de mai sus, se obtin saturatiile în cele doua faze. Sistemul se rezolva pen-tru fiecare pixel.

Când sunt prezente trei faze, spre exemplu titei, gaze si apa, sunt necesare deteminari la doua nivele de energie. O conditie suplimentara este aceea a contrastului mare între cele doua mecanisme de atenuare (împrastierea Compton si absorbtia fotoelectrica). În caz contrar, este necesar adaosul unor aditivi (ex. compusi ai iodului) pentru marirea contrastului. si în acest caz se obtine un sistem, dar cu trei ecuatii:

(14.10.)

(14.11.)

si

(14.12.)

Indicii 1 si 2 se refera la valorile determinate la cele doua energii de emisie.

Având în vedere ca determinarile se pot face pentru orice presiune si temperatura, deci si pentru conditii comparabile cu cele de zacamânt, aceasta lipsa de restrictii face ca tomografia sa poata fi aplicata în cursul unor procese dinamice, cum ar fi curgerea eterogena sau teste de dezlocuire a titeiului cu diferite substante (apa, solutii alcaline, tenside, dioxid de carbon etc.).

Prin înregistrarea sucesiunii imaginilor în diverse sectiuni la anumite intervale de timp, se poate realiza o animatie a proceselor. În felul acesta se poate urmari on-line experimentele de laborator prin imagini bi- sau chiar tridimensionale. Imaginile înregistrate pentru procese similare (spre exemplu dezlocuirea titeiului cu solutii alcaline de concentratii diferite) se pot compara între ele, concluziile putând avea nu numai o componenta cantitativa ci si una calitativa.

Exista si alte aplicatii ale tomografiei computerizate cu raze X. Fara a detalia, vor fi amintite aici numai câteva: determinarea densitatii, a compre-sibilitatii, a porozitatii, a suprafetei specifice ale rocilor, corelarea datelor obtinute prin investigarea geofizica a sondelor cu proprietatile carotelor, studiul invaziei cu fluid de foraj a carotelor etc.

Un interes special îl prezinta cunoasterea starii de saturatie in situ a rocilor traversate prin foraj, pentru a stabili intervalele în care se deschide stratul productiv. Acest interes major a dus la dezvoltarea metodelor geofizice de investigare a sondelor.  

Cu toate progresele spectaculoase înregistrate în geofizica de sonda, nu se poate înca stabili cantitativ starea de saturatie. Unul din motive este si modificarea starii de 13213w2210n saturatie în zona vecina sondei determinata, în principal, de invazia fluidelor de foraj. În schimb, se pot stabili cu o buna precizie intervalele de adâncime pe care rocile sunt saturate cu hidrocarburi. Discutia completa a subiectului este facuta în cursurile de geofizica de sonda [66].

14.3. Starea de saturatie la scara micro

Rolul major al starii de saturatie pentru procesele care au loc în zacamintele de hidrocarburi, în special cele de titei, se refera, în egala masura, la continutul în fluide al rocii (starea de saturatie la scara macro) si la modul în care fluidele respective sunt dispuse în porii rocii (starea de saturatie la scara micro).

Surprinderea pe cale experimentala a asezarii fazelor în pori este destul de dificila, fiind necesare multe artificii experimentale ce nu pot fi descrise aici. Mai comoda, dar si eficienta este studierea la microscop a acestui aspect pe micromodele de roca transparente. Chiar daca nu poate fi reprodusa com-plexitatea mediilor poroase naturale, în masura în care sunt construite în concordanta cu structura spatiului de pori al rocii în cauza, micromodelele ofera o imagine sugestiva a modului de dispunere a fazelor în pori. În cele ce urmeaza, vor fi ilustrate grafic cele mai importante aranjamente spatiale ale fluidelor în pori.

Figura 14.8. ilustreaza dispunerea asa-zis pendulara a unei faze. Caracteristic este faptul ca o faza dispusa pendular ocupa zonele periferice, în special acolo unde sectiunea transversala sufera variatii importante. Simbolul utilizat pe figura este u, pentru ca o astfel de dispunere este caracteristica fazei umezitoare. De asemenea, de o importanta speciala este faptul ca o faza dispusa pendular este discontinua*⁾.

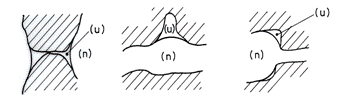
Fig. 14.8. Dispunerea pendulara a fazei umezitoare.

Cealalta faza fluida, notata cu n (neumezitoare), dispusa central, este o faza continua. Caracterul continuu sau discontinuu al dispunerii unei faze în pori este esential pentru întelegerea si descrierea curgerii si a dezlocuirii, dupa cum se va vedea în capitolele urmatoare. De aceea, de fiecare data, se va sublinia acest caracter de continuitate sau de discontinuitate a fazelor.

*) Ca terminologie, se spune despre o faza ca este discontinua daca este marginita de interfete pe un spatiu mic (unul sau mai multi pori, adica pe distante mici, microscopice). Prin antinomie, o faza este continua daca lipsesc interfetele pe distanta mai multor pori si chiar pe distante mari, macroscopice.

O astfel de dispunere este asemanatoare cu dispunerea pendulara din punct de vedere al locului de asezare. Diferenta majora este faptul ca o faza dispusa funicular sau inelar este o faza continua. Trecerea de la dispunerea pendulara la cea funiculara se face prin cresterea saturatiei în faza umezitoare, când are loc coalescenta gradata între elementele de volum situate în apropiere.

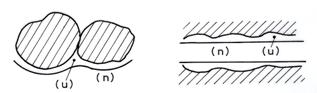
a. b.

Fig. 14.9. Dispunerea funiculara si inelara a fazei umezitoare.

Cealalta faza, faza neumezitoare, dispusa central, poate fi uneori continua, alteori discontinua.

Figura 14.10,a ilustreaza dispunerea insulara a fazei neumezitoare. Aceas-ta dispunere este asociata cu o saturatie mica în aceasta faza care este discon-tinua, fara a afecta, însa, continuitatea fazei umezitoare.

Fig. 14.10. Dispunerea insulara a fazei neumezitoare.

Figura 14.11 ilustreaza dispunerea fazelor sub forma dopurilor. Existenta dopurilor de faza umezitoare sau neumezitoare produce discontinuitatea celeilalte faze, astfel încât, ambele faze sunt discontinui în spatiul respectiv.

Fig. 14.11. Dispunerea sub forma de dopuri.

Ponderea fiecaruia din modurile de dispunere spatiala a fazelor în pori mentionate mai sus depinde de multi factori, între care: geometria interna a spatiului de pori (forma, dimensiunea si distributia pe dimensiuni a porilor), capacitatea de udare la nivel micro (determinata de modul de dispunere a mineralelor în roca si de numarul si natura fazelor fluide), de tensiunea interfaciala, de sensul de variatie a saturatiilor (crestere sau scadere) de histereza de udare etc.

Dintre toate aceste configuratii, cele mai stabile sunt cele sub forma pendulara si sub forma de dop. În cazul dispunerii pendulare, presiunea se exercita dinspre interiorul porului catre suprafata solida (presiunea în faza neumezitoare este mai mare decât în faza umezitoare). De mentionat ca dopurile de faza umezitoare sunt stabile în zona constrictiilor, pe când dopurile de faza neumezitoare între constrictii. Cea mai putin stabila este distributia inelara si cea funiculara datorita ariei mari a interfetei. Cele mai mici perturbatii, legate de miscare sau de variatia saturatiilor, duc la formarea dopurilor si, implicit, la o dispunere discontinua a fazelor. În ceea ce priveste distributia insulara, aceasta se transforma usor în dop prin antrenarea de catre faza umezitoare. Un astfel de dop are tendinta de a se bloca la intrarea într-o constrictie pe care o blocheaza partial sau total, asa cum se poate vedea din figura 14.12.

Mecanismul de blocare reprezinta un efect combinat al dimensiunii mici a sectiunii din aval în comparatie cu cea din amonte si al histerezei de udare. Mai precis, curbura interfetei din zona sectiunii minime (c_r) este mult mai mare decât curbura celeilalte parti a interfetei (c_p), c_r >> c_p.

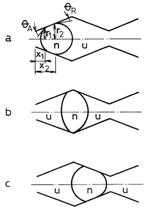
Fig. 14.12. Ilustrarea mecanismului de blocare

a dopurilor de faza neumezitoare între constrictii.

Diferenta capilara de presiune la nivelul dopului este de relatia (13.11.):

(13.11.)

Cu noratiile de pe figura, în pozitia c, expresia (13.11.) devine:

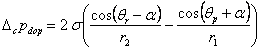(14.13.)

De o importanta capitala pentru procesele de curgere si de dezlocuire reciproca a fazelor este caracterul continuu sau discontinuu al fazelor la nivel micro. Discontinuitatea, adica separarea fazei de referinta prin interfete de celelalte faze, introduce diferente capilare de presiune care genereaza tendinta de imobilizare a fazei în asa-zisele microcapcane capilare sau face dificila miscarea fazei respective.

Determinarea experimentala a modului de distribuire a fazelor în pori este imposibila pe cale directa datorita opacitatii rocii. Informatii interesante se pot obtine pe micromodele transparente.

O metoda de studiu de data recenta [88] permite determinarea distributiei fazelor în pori pe probe reale de roca. Aceasta este cunoscuta sub denumirea de CrioSem si consta în congelarea fluidelor din pori, sectionarea printr-o tehnica speciala a probei de roca si analiza sectiunii la microscopul electronic. Sunt înca foarte putine laboratoare care au pus la punct aparatura si metodologia de lucru pentru aceasta metoda. Rezultatele care se pot obtine prin aceasta metoda, coroborate cu investigarea tomografica, pot furniza informatii de o importanta teoretica greu de anticipat. Este sigur ca în laboratoarele utilate corespunzator se fac astfel de cercetari, chiar daca nu sunt publicate decât sporadic. Este posibil ca în viitorul foarte apropiat sa fie lamurite multe din incertitudinile privind curgerea si dezlocuirea reciproca a fazelor nemiscibile la scara micro, cu implicatii practice si, implicit, economice greu de evaluat.

Aplicatia 1.

Sa se estimeze saturatia în apa aflata sub forma unui film continuu de lichid la suprafata granulelor si fixata în microcapcane capilare pentru un nisip udat preferential de apa. Se cunosc: porozitatea, m= 0,3, suprafata specifica A_s = 1,7 m²/g si densitatea granulelor ρ_s = 2660 kg/m³.

Raspuns.

Saturatia în apa a nisipului, S_a, va avea doua componente: saturatia corespunzatoare volumului de apa din filmul de lichid, S_af, si saturatia corespunzatoare microcapcanelor capilare sub forma inelelor din jurul punctelor (suprafetelor) de contact ale granulelor, S_ac:

Hall si colab. [97] propun pentru saturatia corespunzatoare filmului continuu de lichid relatia:

în care h este grosimea filmului de apa, estimata la: h = 5 - 6 nm.

În ceea ce priveste saturatia în apa fixata capilar, aceeasi autori propun valori determinate experimental în functie de suprafata specifica a nisipului, prezentate în tabelul de mai jos:

Din aplicatia numerica a expresiei pentru S_af si din tabel, rezulta:

S_a =

14.4. Saturatii ireductibile

Studiul experimental al proceselor de dezlocuire reciproca a fazelor nemiscibile în medii poroase au relevat caracterul incomplet al acestui tip de dezlocuire. Cu alte cuvinte, o faza nu va dezlocui niciodata complet o alta faza cu care este nemiscibila, indiferent de modul în care are loc procesul*⁾. Saturatia în faza dezlocuita se reduce pâna la atingerea unei limite inferioare care nu poate fi depasita, în sensul scaderii ei. Aceasta se numeste saturatie ireductibila.

Saturatia ireductibila, notata cu S'_i , trebuie privita în conexiune cu un proces în care saturatia în faza i scade. Pe masura ce saturatia într-o faza scade, gradul de discontinuitate al ei creste, astfel ca la atingerea limitei S'_i faza îsi pierde complet continuitatea, iar cealalta faza (dezlocuitoare) capata un grad de continuitate din ce în ce mai mare. Pentru unele situatii, cum este cresterea saturatiei în gazele iesite din titei sau cresterea saturatiei în lichid la gazele cu condensat, saturatia ireductibila poate fi privita ca limita de la care fazele respective încep sa curga. Initierea curgerii este legata de realizarea continuitatii fazei respective între doua suprafete din roca între care se aplica un gradient de presiune. Cu riscul de a repeta, mentionam ca lipsa de continuitate a unei faze face ca ea sa ramâna imobila chiar prin aplicarea unui gradient de presiune mare.

Saturatiei ireductibile, S'_I, privita la scara macro îi corespunde o gama variata de distributii spatiale a fazei i la scara micro.

Fortele responsabile de existenta saturatiilor ireductibile sunt fortele de interfata, respectiv diferentele capilare de presiune. Se formeaza microcapcane capilare în care se blocheaza mici volume dintr-o faza fluida în diferite zone ale spatiului poros. Punerea lor în miscare necesita forte exterioare mari, pe anumite directii, nedisponibile la scara porilor individuali.

În continuare vor fi descrise si ilustrate prin figuri reprezentative cele mai importante mecanisme de blocare a fazelor în microcapcane capilare. Descrierea se va face separat pentru faza umezitoare si pentru faza neumezitoare. Unele din figurile de mai jos au fost prezentate, din alte puncte de vedere, în acest capitol sau în capitolele anterioare. Unele dintre ele vor fi repetate; repetarea lor este facuta cu scop didactic. Simbolurile sunt cele obisnuite, u pentru faza umezitoare si n pentru faza neumezitoare.

Pentru o faza umezitoare, cel mai important mecanism este fixarea sub forma pendulara (v. fig. 14.8). Explicatia este foarte simpla. De o parte si de alta a interfetei exista o diferenta de presiune (diferenta capilara de presiune) care actioneaza dinspre faza neumezitoare spre faza umezitoare. Presiunea exterioara

se exercita prin intermediul fazei neumezitoare, asa încât, indiferent de marimea presiunii exterioare exercitate pentru punerea în miscare a fazei umezitoare,

*⁾ Aceasta definitie este adevarata în limita unei aproximatii. Fara a intra în delalii foarte tehnice, subliniem faptul ca pentru acelasi sistem format dintr-o roca si doua fluide pragul inferior de saturatie obtinut prin dezlocuire depinde de o serie de factori, dar în limite restrânse.

sensul în care actioneaza este acela de a o bloca si nu de a o evacua din spatiul în care se afla. Modul în care se produce separarea volumului de faza umezitoare care ramâne blocat este aratat în succesiunea de pozitii ale interfetei în miscare (fig. 14.13.).

O situatie interesanta este acela al rocilor neconsolidate unde contactul dintre granule este punctiform sau suprafata de contact este foarte mica. În acest caz, Faza umezitoare se dispune pendular în jurul punctului de contact al granulelor. Interfata are o forma speciala, mult diferita de cele citate pâna aici care erau niste calote sferice. Forma este aceea a unui inel. În planul tangent la granule inelul este

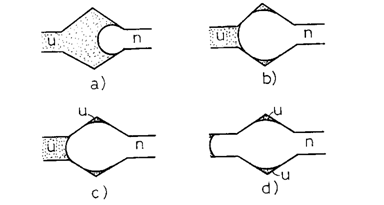
Fig. 14.13. Exemplu de creare a dispunerii pendulare.

concav, iar în planele perpendiculare pe acesta inelul este convex. Cu alte cuvinte, sensul celor doua raze principale de curbura ale interfetei au sens contrar. În figura 2.1.14. este aratata evolutia fenomenului de "stoarcere" a fazei umezitoare pâna la atingerea limitei de continuitate si crearea unui inel imobil în jurul punctului de contact al sferelor.

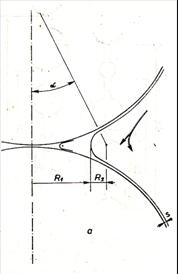
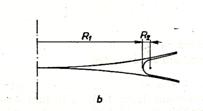
Fig. 14.14. Formarea inelului de faza umezitoare.

Un alt mecanism de fixare este acela în care faza umezitoare este dispusa sub forma de dop. În principiu, un dop de faza umezitoare poate fi în miscare sau în repaus, în functie de efectul combinat al fortelor exterioare (motoare, gravitationala), de frecare si de interfata. Frecarea si histereza de udare au numai un efect de frânare a miscarii. În ceea ce priveste blocarea dopurilor de faza umezitoare, sunt doi factori favorizanti: existenta constrictiilor si a cailor ocolitoare paralele cu porul în care se gaseste dopul. Explicatia existentei microcapcanelor din constrictii are în vedere faptul ca, asa cum s-a aratat în capi- tolul 13, un dop de faza umezitoare este stabil în constrictie, iar traversarea constrictiei presupune exercitarea unei presiuni exterioare mai mari decât diferenta capilara de presiune maxima, care apare atunci când interfata din amonte ajunge în sectiunea minima, adica atunci când diferenta dintre curburile celor doua interfete care marginesc dopul este maxima (v. rel. 13.11.). Daca exista una sau mai multe cai ocolitoare în care se afla numai faza neumezitoare si unde nu se exercita diferente capilare de presiune, curgerea va avea loc numai prin porii respectivi, iar dopul va ramâne imobil. Daca facem din nou mentiunea ca de aflam în situatia în care saturatia în faza umezitoare este mica, este foarte probabil ca un numarul de pori în care se afla numai faza neumezitoare sa fie mare, iar gradul de continuitate al acestei faze sa fie, de asemenea, mare.

O observatie interesanta este aceea ca blocarea fazei umezitoare sub forma de dop atrage dupa sine imobilizarea unui volum mai mare sau mai mic de faza neumezitoare. Mai mult, într-o configuratie nefavorabila de pori este posibila imobilizarea unor volume considerabile de faza neumezitoare în interiorul unei succesiuni de dopuri de faza umezitoare prinse concomitent în microcapcane. Mai precis, de produce blocarea curgerii într-o retea de pori la periferia careia se gasesc dopuri fixe de faza umezitoare. Modul cum se ajunge efectiv la o astfel de dispunere a celor doua faze este mai complicat si nu va fi expus aici.

Faza neumezitoare este blocata în microcapcane capilare mai ales sub forma de dopuri. Modul de fragmentare a fazei neumezitoare într-o succesiune de trunchiuri de con este aratat în figura 14.15.

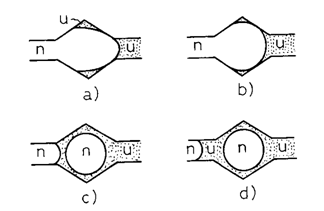
Fig. 14.15. Fragmentarea fazei neumezitoare.

Mecanismul de blocare a fazei neumezitoare între constrictii este ilustrat în figura 14.12.

Valoarea saturatiei ireductibile pentru o anumita faza depinde de un întreg complex de factori. Fara a intra în prea multe detalii, vom mentiona câteva tendinte.

Comparând saturatia ireductibila a unei roci într-o faza umezitoare cu cea pentru o faza neumezitoare este de asteptat ca prima sa fie mai mare decât cea de a doua. Numarul de tipuri de microcapcane pentru o faza umezitoare, asa cum se poate constata din paragrafele urmatoare, este mai mare decât pentru o faza neumezitoare. Forma pendulara de dispunere a fazei umezitoare are o pondere importanta.

Un factor extrem de important este structura spatiului poros, în special distributia porilor pe dimensiuni. Astfel, cu cât ponderea porilor fini este mai mare, cu atât saturatiile ireductibile sunt mai mari. Explicatia este cât se poate de simpla: amplitudinea diferentelor capilare de presiune, responsabile pentru existenta saturatiiloe ireductibile, este mare pentru dimensiuni mici ale porilor.

Un parametru care depinde mult de structura spatiului de pori, permeabilitatea absoluta, se afla în strânsa corelare cu saturatiile ireductibile, în sensul ca rocilor cu permeabilitate absoluta mare le sunt caracteristice saturatii ireductible mici.

Tensiunea interfaciala, coroborata cu contrastul de umidivitate au o influenta importanta asupra saturatiilor ireductibile. Astfel, o tensiune interfaciala mare, alaturi de un contrast mare de umidivitate determina valori mari ale saturatiei ireductibile pentru faza umezitoare din cauza valorilor mari ale diferentei capilare de presiune si exacerbarea blocarii sub forma de dopuri în porii fini si în constrictii. Pe de alta parte, o valoare mica a tensiunii intefaciale împreuna cu un contrast mare de umidivitate conduc la valori mici ale saturatiilor ireductibile pentru faza umezitoare, deoarece blocarea sub forma de dopuri, în porii de dimensiune mare si între constrictii este diminuata.

Histereza de udare, accentuata de viteza mare de dezlocuire, amplifica fragmentarea fazelor, iar valorile saturatiilor ireductibile rezultate vor fi mai mari.

O mentiune importanta se refera la apa ireductibila din zacamintele de hidrocarburi. Ea este rezultatul procesului complex, în buna parte necunoscut, de formare a zacamintelor prin migrarea hidrocarburilor. Esential este faptul ca "primul ocupant" a fost apa. Dezlocuirea apei de catre hidrocarburi nu a urmat acelasi parcurs ca dezlocuirea realizata pe o proba de carota. Mecanismele de migrare sunt mai variate si se desfasoara la alta scara de timp [1]. Spre exemplu, difuzia moleculara poate reprezenta o componenta importanta, mai ales pentru hidrocarburile usoare. În determinarile de laborator, acest mecanism este cu totul nesemnificativ. Caracterul hidrofil sau oleofil al rocii este de asemenea esential în dispunerea apei si hidrocarburilor la scara micro.

Este cunoscut faptul ca saturatia initiala în apa, considerata ca apa ireductibila, variaza, de la zacamânt la zacamânt, în limite foarte largi: de la sub 20% la peste 60%. Acest interval, incredibil de mare, este o dovada a complexitatii sistemului ce se cheama zacamânt, atât din punct de vedere al naturii si proprietatilor rocilor colectoare cât si al naturii si proprietatilor fluidelor de zacamânt. Chiar si în cazul aceluiasi zacamânt limitele de variatie sunt destul de largi, uneori de la simplu la dublu, data fiind variatia de litofacies, uneori foarte marcata.

Determinarile experimentale, respectiv testele de reconstituire a starii initiale de saturatie din zacaminte, au aratat o dependenta marcata a saturatiei ireductibile în apa (saturatia initiala) si permeabilitatea absoluta a rocii. În figura 14.16. este aratata tendinta statistica a relatiei permeabilitate absoluta - saturatie ireductibila pentru doua roci nisipoase [105].

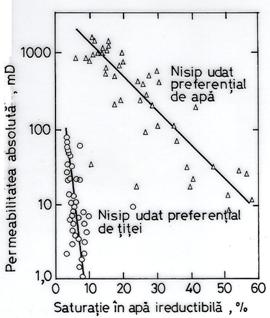
Fig. 14.16. Dependenta dintre permeabilitatea absoluta

si saturatia ireductibila în apa.

Este de remarcat diferenta foarte mare între cele doua nisipuri, unul udat preferential de apa iar celalalt de titei. De asemenea, este remarcabila împrastierea punctelor, ceea ce arata ca exista înca multi parametri care influenteaza valoarea saturatiilor ireductibile. În sfârsit, domeniul de variatie al satuiratiei ireductibile este mult mai mare în cazul nisipului hidrofil decât în cazul nisipului oleofil. Mecanismele de blocare a apei în microcapcane capilare sunt mai putine în cazul unei faze neumezitoare, iar saturatiile ireductibile sunt mai mici, asa cum s-a aratat în câteva paragrafe anterioare.

Prezenta mineralelor argiloase în majoritatea rocilor colectoare este o cauza importanta pentru saturatii ireductibile în apa foarte mari. De altfel, cele mai mari saturatii ireducribile în zona productiva de titei sau de gaze, de peste 50%, sunt asociate cu o fractie mare de minerale argiloase din grupa montmorillonitului si a illitului, precum si o dimensiune mica a porilor.

14.5. Starea de saturatie în zacaminte neexploatate

Exploatarea unui zacamânt de hidrocarburi consta în extractia prin sonde a titeiului si/sau a gazelor. Una din consecinte este modificarea starii initiale de saturatie, adica a starii de saturatie existenta în momentul începerii exploatarii. Modificarea starii de 13213w2210n saturatie este foarte variata si depinde de o multitudine de factori. Prin simulare, se poate obtine un tablou general al evolutiei starii de saturatie. Pentru ca acest tablou sa fie cât mai fidel, trebuie ca initializarea lui sa fie cât mai correcta.

În subcapitolul precedent, referitor la saturatiile ireductibile, s-a mentionat ca orice proces de dezlocuire este incomplet, inclusiv acela prin care apa preexistenta în roca colectoare este dezlocuita de hidrocarburi în procesul de formare a zacamintelor. Asadar, în zacamânt exista o saturatie ireductibila în apa. În masura în care roca colectoare este omogena si izotropa, iar extinderea zacamântului este limitata, este de asteptat ca saturatia ireductibila în apa sa fie o constanta pentru zacamânt. În realitate, se poate vorbi doar de o valoare medie pe zacamânt, limitele de variatie putând fi foarte largi, chiar de la simplu la dublu sau mai mult, în functie de litologia si extinderea zacamânului precum si de modul de formare a zacamântului.

În zona cea mai coborâta a zacamântului este localizat acviferul, adica o zona saturata complet în apa (mai corect, aproape complet, pentru ca exista urme sau cantirati mici de hidrocarburi libere; sunt excluse în discutia de fata gazele dizolvate în apa). Contactul dintre cele doua zone, saturate cu apa si, respectiv, cu hidrocarburi (denumite în mod curent acvifer si, respectiv zona productiva) nu este unul obisnuit, asa cum ar fi într-un rezervor de mari dimensiuni, adica o suprafata aparenta de separatie. Data fiind prezenta rocii, adica a unei retele de pori cu caracteristici geometrice speciale, asa cum a fost descrisa în capitolul 7, contactul dintre apa si hidrocarburi este localizat în pori cu dimensiuni capilare, unde se manifesta intens fortele de interfata.

Pentru usurinta întelegerii, se considera un model simplist pentru roca: un fascicul de capilare cilindrice cu raze diferite. Asa cum s-a aratat în capitolul 11, înaltimea de ascensiune sau de depresiune capilara depinde în mod direct de sectiunea (raza) capilarului. Legatura dintre marimile care intervin în fenomenul ascensiunii sau depresiunii capilare este data de relatia (vezi cap. 11.):

Asadar, contactul (interfata) apei cu hidrocarburile se gaseste la cote diferite, cu atât mai ridicate cu cât raza capilarului este mai mica. În cazul ascensiunii capilare (când faza umezitoare este apa), putem vorbi de o cota minima, corespunzatoare celui mai larg por si o cota maxima, corespunzatoare celui mai îngust por. Sub cota minima, saturatia în apa este maxima (S_a = 1) iar peste cota maxima, saturatia în apa este minima (S_a = 0). Între cele doua limite saturatia în apa scade, constituindu-se ceea ce se numeste zona de tranzitie. Modul de variatie a saturatiei în apa (si, în mod complementar, în hidrocarburi) depinde de distributia pe dimensiuni a capilarelor. Un experiment simplu care surprinde acest fenomen este prezentat în [18].

În fapt, lucrurile sunt cu mult mai complicate. Modelul invocat mai sus surprinde numai cea mai importanta caracteristica a rocii legata de acest fenomen: distributia porilor pe dimensiuni. Principala limita se refera la imposibilitatea modelarii saturatiei ireductibile. O alta limita se refera la modul complex de dezlocuire într-o retea de pori fata de dezlocuirea pe un fascicul de capilare.

Chiar daca este greu de descris, echilibrul fortei de gravitatie cu fortele de interfata se realizeaza în conditiile formarii unei zone de tranzitie între acvifer si restul zacamântului. Caracteristica principala a zonei de tranzitie este variatia saturatiei de la unitate la saturatia ireductibila.

Un fenomen asemanator are loc si la contactul dintre titei si cupola de gazele din cupola, atunci când ea exista. Pentru ilustrare, în figura 14.17 este prezentata distributia saturatiei pe înaltime într-un zacamânt de titei cu cap liber de gaze. Se disting cinci intervale: acviferul, zona de tranzitie apa-titei, zacamântul de titei propriu-zis, zona de tranzitie titei-gaze si capul de gaze. Starea de saturatie din fiecare interval este precizata pe figura.

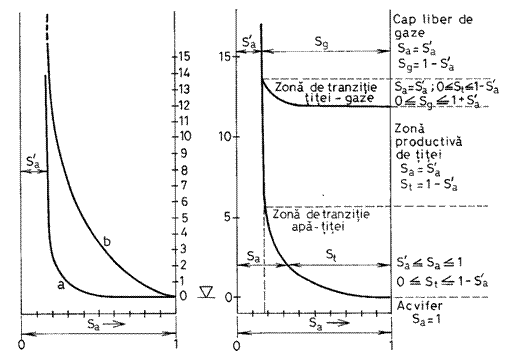
Fig. 14.17 Distributia saturatiilor într-un zacamânt neexploatat.

Fata de situatia prezentata se disting alte doua cazuri particulare: în zacamânte de titei fara cupola de gaze si în zacamânte de gaze sau de gaze cu condensat în care exista numai câte o zona de tranzitie.

În ceea ce priveste extinderea si alura curbei de variatie a saturatiei în zona de tranzitie, ele sunt specifice fiecarui zacamânt. Din relatia (11.8.) se pot identifica parametrii care le influenteaza. Cel mai important factor este distributia porilor pe dimensiuni. Cu cât porii sunt mai fini, cu atât zona de tranzitie este mai extinsa. Unui grad mare de neuniformitate îi corespunde o trecere mai gradata între cele doua limite ale saturatiei. Un alt factor important este contrastul de densitate între faze. Zona de tranzitie apa-gaze este mult mai restrânsa decât zona de tranzitie apa-titei. Tensiunea interfaciala joaca un rol minor pentru ca limitele de variatie sunt relativ restrânse, asa cum s-a aratat în capitolul 11. O mentiune speciala trebuie facuta în ceea ce priveste capacitatea de udare a rocii fata de fluidele în contact. Daca pentru perechile apa-gaze si titei-gaze situatia este simpla, în sensul ca cele doua lichide reprezinta faza umezitoare, procesul fiind unul de ascensiune capilara, pentru perechea apa-titei poate avea fie o ascensiune, fie o depresiune capilara a apei, dupa cum apa este faza umezitoare sau neumezitoare în raport cu titeiul.

Pe lânga considerentele teoretice, existenta zonelor de tranzitie este probata si de masuratorile geofizice.

Stabilirea extinderii zonelor de tranzitie este importanta atît pentru evaluarea resurselor de hidrocarburi prin metoda volumetrica, cât si pentru stabilirea intervalelor de perforare. Fara a intra în detalii, este usor de admis ca daca se considera un volum de roca saturat cu hidrocarburi delimitat de acvifer, luând în considerare zona de tranzitie ca zona productiva, resursa va fi supraevaluata, în zona de tranzitie existând un volum considerabil de apa. Este la fel de usor de admis ca daca se perforeaza coloana în dreptul zonei de tranzitie sonda va produce si apa înca de la debutul exploatarii.

Aplicatia 2.

Se considera modelul de roca fictiva. Sa se determine saturatia în faza umezitoare dispusa pendular, sub forma unor inele în jurul punctelor de contacr ale sferelor pentru diferite presiuni exterioare de dezlocuire.

Raspuns.

Se vor folosi notatiile din figua:

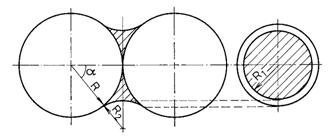
Volumul inelului de faza umezitoare, calculat ca volumul unui corp de rotatie este dat de expresia:

în care s-a tinut seama ca:

Saturatia în faza umezitoare este data de relatia:

în care N este numarul de inele (de puncte de contact, iar V_p este volumul de pori (pentru un volum brut unitar, V_p = m, m fiind porozitatea rocii).

Numarul de puncte de contact de numarul de sfere, n, si, implicit, de raza sferelor si de modul de impachetare. Se considera cele doua moduri de impachetare extreme: cubica si tetraedrica (romboedrica) care corespund numarului minim, respectiv maxim de sfere dintr-o unitate de volum brut de roca.

Numarul de sfere dintr-o unitate de volum brut se poate calcul, plecând de la definitia porozitatii, cu relatia:

Numarul de puncte de contact se poare calcula, din considerente geometrice simple, pentru cele doua moduri de impachetare mentionate (cubica, indicele c si romboedrica, indicele r) cu relatiile:

Saturatia rezulta imediat, din definitie:

în care

Daca se tine seama ca m^c = 0,4764, iar m^r = 0,2597, rezulta, pentru saturatie, relatiile:

respectiv,

Valoarea lui α si, implicit a functiei f(x) depind de pozitia interfetei care, la rândul ei este determinata de presiunea exterioara care realizeaza dezlocuirea fazei umezitoare

Aplicatia 3.

Sa se reprezinte grafic starea de saturatie a unei carote din momentul desprinderii ei dintr-un zacamânt de titei, pâna in laborator.

Raspuns.

Se poate defini mai întâi o stare "zero" aceea a rocii colectoare sterile, înainte de formarea zacamântului (punctul 0 din figura), când roca este complet saturata cu apa. Este foarte mica probabilitatea ca roca-mama de petrol sa ajunga sa constituie o roca-magazin, economic exploatabila.

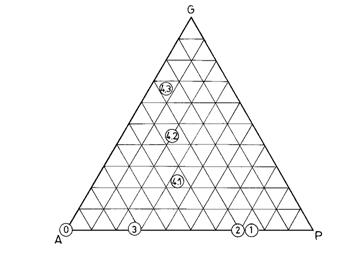
Starea initiala de zacamânt, când roca contine apa la saturatia ireductibila, restul fiind titei: punctul 1 pe figura.

Starea initiala de fund se refera la locul unde urmeaza sa ajunga o sonda noua îintr-un zacamânt la care a început exploatarea. Este posibil sa fie întâlnita starea initiala de zacamânt sau, cu o anumita probabilitate, o stare de saturatie apropiata, dar cu o saturatie putin crescuta în apa: punctul 2 pe figura.

Starea actuala de fund are în vedere momentul desprinderii carotei din masa rocii colectoare, cu alte cuvinte dupa ce instrumentul de carotare a traversat zona pe care, într-o masura mai mare sau mai mica a afectat-o, în sensul ca s-a produs o invazie a fluidului de foraj. Daca fluidul de foraj este pe baza de apa, este asteptata o scadere drastica a saturatiei în titei, uneori catre saturatia ireductibila. Daca fluidul de foraj este pe baza de produse petroliere, fara continut de apa, saturatia în apa se conserva. Cum prima situatie este cea mai frecventa, aceasta stare de saturatie este desemnata în figura prin punctul 3.

Starea actuala de suprafata desemneaza situatia prezenta în carota dupa extragere, ambalare si transport în laborator. Modificarile produse asupra starii de saturatie sunt foarte importante. Procesul dominant este cel al iesirii gazelor din solutie la scaderea presiunii, pe masura ce carota este extrasa spre suprafata. Volumul de gaze libere care ies din carota, producând dezlocuirea titeiului si a apei, este de câteva ori mai mare decât volumul de pori ai carotei pentru un titei mediu. În cazul titeiurilor volatile volumul de gaze care parasesc carota este cu un ordin zecimal de marime superior celui al titeiurilor grele, procesul de dezlocuire fiind mai avansat. Mecanismul dezlocuirii este mult mai complicat decât pare la prima vedere, el fiind influentat de o serie întreaga de factori care vor fi pusi în discutie în capitolele urmatoare. Rezultatul acestui proces este consemnat generic pe figura prin punctele 4.1...4.3. Scaderea saturatiei în apa se produce si prin vaporizare (si nu evaporare).

În acest context, este interesant de mentionat ca unele carote par lipsite de titei fiind "curate", în timp ce altele sunt intens colorate, semn al existentei unei saturatii importante în titei. Existenta unei saturatii mari în titei a carotei este un indiciu al unei eficiente inferioare a exploatarii zacamântului din care provine. Paradoxul este numai aparent. Faptul ca titeiul a fost eficient dezlocuit din carota este un indiciu pentru o situatie similara în timpul exploatarii zacamântului.

Întrebari si probleme

Care este diferenta între coeficient de saturatie si stare de saturatie a unei roci?

Cum se scrie ecuatia de bilant de volume prin saturatii?

De ceste utila reprezentarea grafica a starii de saturatie a unei roci?

Care sunt limitele de variatie ale coeficientilor de saturatie?

Prin ce se aseamana dispunerea insulara si cea sub forma de dop a unei faze? Dar dispunerea funiculara cu cea inelara?

De ce se numesc distructive unele metode de determinare a starii de saturatie?

De ce se introduc substante cu masa moleculara mare în apa sau în titei la analiza tomografica?

Care sunt informatiile principale obtinute prin tomografia computerizata a probelor de roca?

Cum se realizeaza profilele de saturatie în diferite sectiuni prin roca?

De ce se folosesc doua nivele energetice pentru determinarea starii de 13213w2210n saturatie când sunt prezente trei faze?

Ce este saturatia ireductibila? Care sunt principalii parametri care o determina?

Care este caracteristica principala a distributiei unei faze la saturatia ireductibila?

Care sunt limitele de variatie a saturatiilor ireductibile?

Cum se determina saturatia ireductibila?

Sa de evalueze diferenta de presiune necesara pentru a forta un dop de faza neumezitoare sa traverseze o constrictie formata de doua trunchiuri de con cu unghiul la vârf de 60⁰ si cu o raza minima de 0,01 mm daca volumul dopului este egal cu volumul trunchiului de con. Unghiurile de contact regresiv si progresiv sunt de 30⁰, respecti 60⁰, iar tensiunea interfaciala de 0,04 N/m.

Aceeasi problema pentru un dop de faza umezitoare.

În ce consta diferenta între saturatia ireductibila si saturatia reziduala în titei?

Sa se traseze curba de variatie a saturatiei în apa în zona de tranzitie pentru urmatoarea situatie simplificata: saturatia ireductibila în apa de 30%, unghiul de contact masurat în apa de 30⁰, tensiunea interfaciala de 0,04 N/m, diferenta de densitate între apa si titei de 200 kg/m³, iar porii sunt modelati prin canale cilindrice cu urmatoarea distributie pe dimensiuni (fara porii care cantoneaza apa ireductibila): 10% cu raza de 0,01 mm, 40% cu raza de 0,04 mm, 20% cu raza de 0,08 mm, 20% cu raza de 0,15 mm si 10% cu raza de 0,4 mm. Indicatie: pentru calculul saturatiilor pe diferitele intervale de înaltime de ascensiune corespunzatoare razelor respective, se considera doar 0,7 din volumul de pori.

Sa se faca o paralela între curbele de variatie a saturatiei pe înaltime în zona de tranzitie apa-titei pentru cazul în care faza umezitoare este apa, respectiv titeiul.

De ce este mai extinsa zona de tranzitie apa-titei decât zona de tranzitie titei-gaze din acelasi zacamânt?