Structura populatiilor

Distributia populatiilor este determinata de spatiul disponibil, de marimea habitatului care influenteaza modul de viata a populatiilor, functionalitatea acestora atât sub aspectul presiunii factorilor abiotici asupra populatiilor cât si în relatie cu alte populatii din cadrul biocenozei caracteristice arealului respectiv.

12.1 Structura spatiala si temporala

Habitatul populatiei poate fi descris în sens mai larg, luând în consideratie factorii climatici sau numai climatul general sau mult mai exact, tinând cont de elemente de detaliu ale biotopului cum sunt tipul de sol, categoria de ape etc. Toate aceste elemente au însa un impact major asupra modului în care se realizeaza distributia populatiilor.

Distributia pe scara larga a organismelor poate sa depinda de valorile de temperatura sau de precipitatii extreme asociate sau nu cu temperatura. Cu toate acestea, rareori vom întâlni aceeasi specie în toate zonele geografice care prezinta valori adecvate pentru existenta speciei. Acest fapt conduce la concluzia ca exista si alti factori care determina capacitate speciilor de a trai în diversele microclimate oferite de varietatea biotopilor.

Un alt factor care determina prezenta sau absenta unei specii într-un anumit tip de habitat este abilitatea organismelor sa ajunga într-o anumita zona geografica. Distantele mari reprezentate de zone inospitaliere (deserturi, lanturi muntoase, bazine acvatice) limiteaza drastic posibilitatea organismelor de coloniza anumite habitate, chiar în ipoteza ca acestea prezinta conditii favorabile dezvoltarii speciei. De aceea, adaptarea organismelor la o dispersie de succes în mediu, are un rol important în raspândirea speciilor. De obicei au succes speciile de plante ale caror seminte sunt raspândite de vânt si animalele care pot zbura pe distante mai mari.

Dimensiuni habitatelor adecvate si distantele care le separa determina heterogenitatea spatiala. Exista multe cazuri reale în care indivizii unor specii au tendinta de a se aglomera un unele areale si exista de asemenea cazuri în care, în alte habitate indivizii se regasesc, m 939u2017j ai mult sau mai putin, izolat.

Dimensiunea habitatului va determina si modul în care speciile vor coloniza habitatul respectiv, dar si longevitatea populatiilor într-un anumit habitat, în sensul ca o suprafata restrânsa poate sustine o populatie limitata numeric ceea ce determina o probabilitate crescuta ca în anumite conditii (defavorabile) populatia sa poate ajunge la extinctie mult mai repede decât în biotopurile mai extinse. De aceea, în aceste habitate, se poate manifesta o discontinuitate a prezentei uneia sau mai multor specii. În cazurile în exista mai multe habitate, de obicei de dimensiuni reduse, care suporta anumite populatii pentru perioade relativ reduse de timp, ansamblul populatiilor care populeaza aceste habitate este denumit metapopulatie.

Abilitatea unor organisme de a coloniza astfel de habitate marginale determina cresterea distributiei speciei si utilizarea frecventa a acestor spatii geografice permite selectiei naturale sa se manifeste asupra unor populatii, fapt ce poate conduce la noi adaptari specifice.

Într-un anumit habitat, indivizii unei populatii pot trai mai mult sau mai putin izolat unii fata de altii. Marimea care descrie acest comportament se numeste dispersie sau distributie spatiala a populatiei.

Din acest punct de vedere, indivizii unei populatii pot fi grupati sau dispersati (cazuri extreme) sau distribuiti întâmplator (randomizat). Dispersia indivizilor este, desigur, dependenta de disponibilitatea resurselor (de exemplu, resursele trofice), dar este influentata si de relatiile cu alti indivizi ai populatiei. Populatiile cu un comportament social mai pronuntat au tendinta de a trai mai grupat, în timp ce organismele la care componenta antagonista a relatiilor este mai pronuntata sunt mai dispersati în cadrul arealului.

12.2. Distributia spatiala a populatiei

Modul în care sunt distribuiti în arealul lor indivizii unei populatii naturale de organisme este de asemenea si un indicator ecologic important cu implicatii în dinamica populatiilor, influentând în mod direct densitatea organismelor.

Principalele trei tipuri de baza ale distributiei spatiale care se iau de regula în consideratie sunt reprezentate grafic în figura 36. Modul cel mai simplu de determinare a tipului de distributie spatiala pentru o anumita populatie este utilizarea metodelor statistice care pot aprecia cu un anumit grad de precizie daca populatia este distribuita dupa unul din tipurile teoretice de distributie.

Fig. 36. Reprezentarea grafica a principalelor tipuri de distributie spatiala

12.2.1. Distributia spatiala randomizata

Distributia spatiala randomizata poate fi simulata utilizând seria Poisson ca distributie teoretica. Pentru a întelege acest lucru prezentam în continuare un exemplu foarte simplu.

Sa presupunem ca un numar de 100 de pescari pleaca la pescuit pe acelasi bazin acvatic si pescuiesc pe parcursul aceluiasi interval de timp. Teoretic fiecare dintre ei are aceeasi probabilitate de a captura un peste pe unitatea de timp, însa în realitate ei realizeaza capturi diferite.

În tabelul de mai jos se prezinta corelatia dintre numarul de pescari si numarul de pesti capturati, proportia pescarilor care au prins un anumit numar de pesti si distributia Poisson asociata.

Tabel nr. 13. Distributia reala a valorilor si distributia teoretica asociata.

Valoarea mediei numarului de pesti capturati de un pescar este M = 2,30, iar deviatia standard este SD = 1,41.

Distributia Poisson este descrisa de ecuatia:

în care: m = media arithmetica; i = valoarea capturii (numar de pesti)

i! = i factorial (reamintim ca: 0! = 1)

Trebuie sa tinem cont de faptul ca în cazul seriei Poisson, media (m) este egala cu varianta (s²).

Pentru a verifica daca distributia reala a valorilor din exemplul prezentat este sau nu semnificativ diferita de distributia teoretica (seria Poisson) se utilizeaza testul χ², utilizând relatia:

în care:

n(i) = distributia reala, în cazul de fata, numarul de pescari care au capturat i pesti (valori observate);

n'(i) = distributia teoretica, ceea ce înseamna, valoarea teoretica a numarului de pescari ce ar trebui sa captureze un numar i de pesti, conform seriei Poisson (valori teoretice).

În cazul numeric prezentat mai înainte valoarea calculata a lui χ² este 4,74. Numarul de grade de libertate este egal cu numarul claselor de distributie, care în cazul particular luat ca exemplu este 7, din care se scade numarul de parametri care au fost utilizati pentru a ajusta distributia teoretica la distributia reala. În exemplul de fata, s-au utilizat 2 parametri, mai exact media aritmetica (m) si numarul total de pescari (N), de unde rezulta ca numarul gradelor de libertate (gl) este 5 (gl

Care este însa legatura dintre exemplul prezentat si modul de determinare a distributiei spatiale? Pentru a întelege acest lucru trebuie sa ne imaginam ca analizam o populatie prin numararea organismelor de pe o unitate de suprafata (de exemplu, 1 ha). Un acest caz, fiecare unitate de suprafata este echivalenta unui pescar iar numarul de exemplare numarate este echivalent cu numarul de pesti capturati.

Uneori, atunci când este necesara o apreciere rapida a tipului de distributie spatiala, se poate utiliza o determinare rapida a coeficientului de dispersie (Cd) dupa relatia:

Daca:

Cd este semnificativ mai mic decât 1, atunci distributia spatiala este uniforma.

Cd este aproximativ egal cu 1, atunci distributia spatiala este randomizata.

Cd este semnificativ mai mare decât 1, atunci distributia spatiala este grupata.

Evolutia seriei Poisson pentru diferite valori ale mediei este prezentata în figura 37.

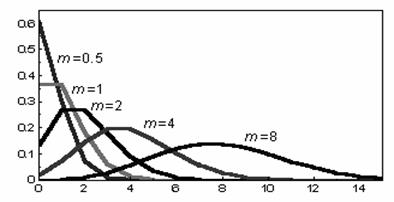
Fig. 37. Serii Poisson trasate în functie de diferite valori ale

mediei aritmetice

Din figura de mai sus se poate observa ca seriile (distributiile) Poisson sunt asimetrice pentru valori mici ale mediei si respectiv aproape simetrice pentru valori mari ale mediei aritmetice. Cresterea la infinit a mediei determina coincidenta seriei Poisson cu distributia normala.

12.2.2. Distributia spatiala grupata

Pentru a descrie distributiile spatiale grupate nu exista un model teoretic universal valabil. Exista însa modele empirice care pot fi utilizate în multe cazuri cu rezultate acceptabile. Un astfel de mode este distributia binomial negativa care este descrisa de ecuatia:

în care:

m = media aritmetica;

k = coeficient de agregare (grupare), invers proportional cu cresterea gradului de grupare.

Pentru valoarea nula a variabilei (i= 0) rezulta:

Ceilalti termeni pot fi estimati prin relatia:

Parametrii distributiei binomial negative se estimeaza folosind metoda momentelor. Astfel, rezulta valorile m = M si:

Se observa ca pentru o distributie întâmplatoare (randomizata) care are coeficientul de dispersie Cd = 1 si deci k devine infinit, distributia binomial negativa coincide cu seria Poisson.

12.3. Analize geostatistice

ale distributiei populatiei

Ideea principala a metodelor geostatistice este aceea de a pune în evidenta relatia dintre variatia spatiala a densitatii populatiilor si distanta (spatiul) care le separa. În acest scop trebuie mai întâi sa precizam câteva instrumente care sunt utilizate în acest tip de analiza.

Corelograma directionala ρ(h) se defineste ca fiind o corelatie între efectivele populatiei în punte separate printr-o distanta (interval) h. Dar h este mai degraba o marime vectoriala si nu una scalara.

Spre exemplu, daca h=(10,5), aceasta înseamna ca fiecare pereche de probe comparate vor fi separate de distante de 10 si respectiv 5 (metri, kilometri etc.) pe fiecare directie spatiala considerata.

Evident ca practic este foarte greu sa se poata gasi suficient de multe puncte (statii) de recoltare a probelor care sa fie separate de exact aceeasi distanta reprezentata de vectorul h. Acesta este motivul pentru care se considera toti posibilii vectori h împartiti pe clase.

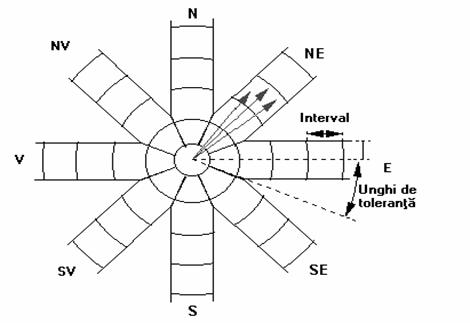
Fig. 38. Reprezentarea unui numar de opt directii spatiale

pentru corelograma directionala

Vectorii h care se afla în aceeasi zona sunt grupati într-o singura clasa iar valoarea corelogramei este estimata separat pentru fiecare clasa. Numarul de directii spatiale luate în considerare poate fi diferit în functie de precizia reprezentarii sau de cantitatea de informatii. Astfel se pot reprezenta 4, 8, 16 etc., directii geografice (figura 38).

Corelograma se estimeaza cu ajutorul ecuatiei:

în care:

-h, +h = indici care arata ca statia de prelevare a probei este situata la începutul sau la sfârsitul vectorului h;

Z_-h, Z_+h = numarul de organisme înregistrate în unitati de proba separate prin valoarea lui h;

N_h = numarul de perechi de unitati de proba separate de vectorul h;

M_-h, M_+h = valorile medii ale probelor situate la capetele vectorului h;

S_-h, S_+h = deviatia standard pentru valorile situate la capetele vectorului h.

Covarianta ofera o alta posibilitatea de a aprecia dependenta spatiala:

Se poate de asemenea utiliza variograma:

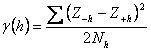
Exista o legatura între corelograma, covarianta si variograma. Daca media populatiei si varianta sunt constante în zona de prelevare a probelor, atunci:

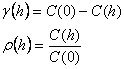
în care, C(0) este covarianta la valoarea h=0. În acest caz, covarianta este egala cu varianta si patratul deviatiei standard. Variograma are forma generala de genul celei prezentate în figura 39.

12.4. Dimensiunea fractala

a distributiei populatiei

Fractalul poate fi definit ca fiind rezultatul repetarii la scara din ce în ce mai mica a unei figuri geometrice în scopul obtinerii unor forme si suprafete neregulate care nu por fi reprezentate prin geometria clasica.

Fractalii sunt utilizati mai ales în  modelarea pe computer a formelor si structurilor existente în natura. De aici si ideea utilizarii lor în studiul ecologic, mai ales pentru a reprezenta alte dimensiuni ale distributiei spatiale a populatiilor.

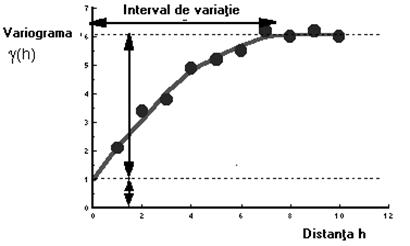
Fig. 39. Reprezentarea generala a variogramei.

Într-o acceptie mai veche, fractalul era definit ca o figura geometrica similara cu ea însasi la toate scarile spatiale. Era rezultatul parcurgerii unui numar infinit de etape, reprezentate schematic în figura 40.

Fig. 40. Primele etape în constructia grafica a fractalilor.

Desi exemple de fractali erau cunoscute de matematicieni de mai mult timp, notiunea a fost fundamentata de Mandelbrot, 1977 (figura 42).

Într-o acceptie mai noua, fractalul este o figura geometrica ce are dimensiuni fractionare. Nu este ceva neobisnuit sa se stabileasca prin numarare dimensiunile unei figuri geometrice. Aceste pot fi definite ca un numar infinit de puncte cu distante specifice pentru fiecare pereche de puncte.

Problema care se pune este cum sa se numere, cum sa se stabileasca dimensiunile unei asemenea figuri geometrice. Unii matematicieni au sugerat sa se considere numarul minim de sfere egale care acopera întreaga figura geometrica.

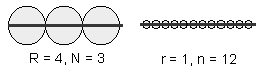
Pentru ca numarul de sfere (N sau n) necesare pentru a masura o figura geometrica este dependent de raza sferei (R sau r), dimensiunile au fost definite prin urmatoarele raporturi:

Spre exemplu, dimensiunea unei linii este egala cu unitatea:

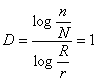
Figurile geometrice clasice, adica simple au dimensiuni întregi, adica 1 pentru o linie, 2 pentru un patrat, 3 pentru un cub, în timp ce fractalii au dimensiuni "fractionale", asa cum se poate observa din figura 41.

În acest caz, pentru un patrat se obtine dimensiunea D=2,01 în loc de valoarea D=2 cum ar fi fost normal.

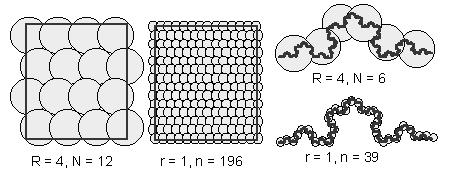
Fig. 41. Modul de stabilire a dimensiunilor fractalului.

Dimensiunile au fost estimate astfel:

-pentru patrat: 

-pentru fractal:

Fig. 42. Fractalul Mandellbrot

Dimensiunea fractala (D) poate fi pusa în legatura cu traiectoria variogramei trasate în coordonate logaritmice (figura 43).

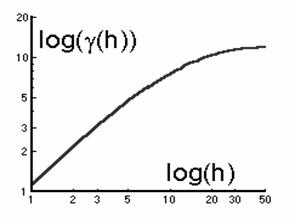
Fig. 43. Forma variogramei trasate în coordonate logaritmice.

12.5. Corelatia dintre factorii de mediu

si densitatea populatiei

Exista o diversitate de modele statistice utilizate pentru a analiza corelatiile existente între densitatea populatiei si diferitii factori de mediu ai caror parametri se modifica din punct de vedere spatial sau temporal, cum ar fi temperatura, regimul precipitatiilor, oxigenul solvit (în cazul ecosistemelor acvatice), concentratia ionilor de hidrogen (pH-ul) solului sau apei etc.

Aceste modele pot fi utilizate pentru a prognoza evolutia efectivului unei populatii în viitor, pentru un ecosistem supus studiului, dar si pentru ecosistemele înca necercetate sub aspectul densitatii populatiilor.

Informatiile dar mai ales datele ce vor trebui prelucrate statistic si integrate modelului pot fi de trei feluri:

serii temporale, care reprezinta un set de masuratori realizate pe o anumita perioada de timp în aceeasi locatie spatiala;

serii spatiale, reprezentând o serie de masuratori efectuate simultan sau în diverse etape, dar localizate în diferite zone ale arealului studiat;

serii mixte, care nu sunt altceva decât un set de serii temporale rezultate din masuratorile efectuate în diferite sectoare ale zonei cercetate.

Modelele statistice sunt de obicei reprezentate de ecuatii liniare sau ecuatii polinomiale. De exemplu, un model liniar va fi caracterizat de o ecuatie de forma:

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + ...

un model polinomial va avea la baza o ecuatie de genul:

y = b₀ +b₁x + b₂x² + b₃x³ + ...

un model polinomial cu mai multi factori va fi descris de ecuatia:

y = b₀ + b₁x₁ + b₂x₂ + b₃x₁x₂ + b₄x₁² + b₅x₂² + ...

în care:

y - este variabila care trebuie prognozata, în cazul de fata, densitatea populatiei;

x_i, b_i - sunt parametri care se determina utilizând analiza regresiei.

Modelul autoregresiv este un model are la baza regresia, în care valoarea variabilei dependente este prognozata din valorile aceleiasi variabile masurate în diferite momente sau în zone adiacente celei pentru care se realizeaza modelarea.

Spre exemplu, densitatea unei populatii de pesti ce ar pute fi realizata anul viitor într-un anumit ecosistem acvatic, poate fi deseori prognozata plecând de la densitatea actuala sau de la densitatile înregistrate în anii anteriori. De asemenea, în modelele de tip autoregresiv, se pot introduce variabile care sa descrie factori ai mediului abiotic, cum sunt factorii climatici, sau actiunea antropica (de exemplu, presiunea efortului de pescuit).

Desigur, geostatistica este o metoda mult mai adecvata pentru modelarea spatiala a evolutiei densitatii unei populatii decât regresia standard, deoarece este posibila utilizarea spatiului tridimensional, cu doua coordonate spatiale si una temporala, rezultând astfel modele spatio-temporale.

Totusi, în aceste modele nu sunt reprezentate mecanismele intime care determina corelatia dintre densitatea populatiei si factorii ecologici. În consecinta, prognoza se realizeaza numai pe baza comportamentului anterior al ecosistemului sau al sistemului populational, considerându-se ca daca anterior sistemul a avut un anumit tip de comportament este foarte posibil ca cel putin în viitorul apropiat, acest comportament sa nu se schimbe în mod semnificativ.

Deci, modelele statistice se bazeaza pe supozitia ca sistemul are un comportament cunoscut si invariant si de aceea ele au o importanta limitata pentru prognozarea noilor comportamente ale sistemului.

12.6. Structura populatiei

în functie de vârsta

Multe populatii sunt adesea formate din indivizi care au vârste diferite, fapt ce este într-o relatie directa cu procesul de reproducere, în sensul ca indivizii tineri nu participa la reproducere, adultii mai tineri pot avea o descendenta crescuta (natalitate mare), exemplarele adulte de vârste mai mari pot avea o descendenta redusa sau pot sa nu participe de loc la reproducere. Repartizarea conventionala a numarului de indivizi în diverse clase de vârsta se numeste distributia vârstelor.

Distributia vârstelor influenteaza în mod direct modul în care se comporta întreaga populatie în propriul habitat si poate caracteriza habitatul din acest punct de vedere. Daca în populatie exista un numar mare de exemplare tinere dar un numar redus de indivizi adulti, concluzia poate fi ca habitatul este adecvat pentru reproducere, dar rata supravietuirii este redusa, în timp ce situatia contrara (adulti numerosi si exemplare tinere putine) poate indica lipsa conditiilor favorabile reproducerii.

Ceea ce este poate mult mai important este faptul ca distributia pe vârste a populatiilor poate oferi informatii utile referitoare la evolutia viitoare a populatiei. Tabelele de viata care evidentiaza distributia claselor de vârsta pot furniza de asemenea mult mai multe informatii, cum ar fi succesul reproducerii pentru fiecare clasa de vârsta, vârsta medie a unei generatii si speranta de viata.

Pentru realizarea tabelelor de viata sunt necesare trei tipuri de date. Primul tip se refera la vârsta indivizilor care se noteaza cu x. Al doilea tip de date se refera la numarul de exemplare din fiecare clasa de vârsta (n_x), iar al treilea la media fecunditatii indivizilor din fiecare clasa de vârsta.

Pornind de la aceste informatii si date se pot calcula urmatoarele valori:

l_x - proportia initiala a indivizilor în viata la vârsta x;

q_x - proportia indivizilor de vârsta x care vor muri;

s_x - supravietuirea specifica vârstei;

e_x - speranta de viata pentru un individ de vârsta x;

v_x - valoarea reproductiva a unui individ la vârsta x;

T - vârsta medie a unei generatii;

R₀ - rata neta a reproducerii.

Dupa calculul tuturor valorilor, se poate realiza un tabel de viata care va avea forma celui prezentat în tabelul 14.

Tabel nr.14. Tabel de viata pentru o populatie ipotetica cu noua clase de varsta.

Supravietuirea (l_x) specifica fiecarei clase de vârsta se calculeaza cu usurinta, deoarece reprezinta numarul de indivizi în viata la vârsta x împartit la numarul de indivizi în viata la vârsta anterioara care defineste clasa de vârsta precedenta (n_x/n₀). Spre exemplu, conform tabelului de viata de mai sus, supravietuirea la vârsta 4 este: 144/843 = 0,171.

Mortalitatea (q_x) se calculeaza de asemenea simplu, fiind de fapt diferenta dintre numarul de indivizi de vârsta x si numarul de indivizi de vârsta x+1, împartit la numarul de indivizi de vârsta x, adica:

Spre exemplu, pentru vârsta 3, mortalitatea are valoarea (316-144)/316 = 0,544.

Supravietuirea caracteristica unei clase de vârsta reprezinta probabilitatea ca un individ sa supravietuiasca de la vârsta x la vârsta x+1 si reprezinta proportia inversa a mortalitatii, adica (1-q_x).

Pornind de la estimarea acestor valori se pot calcula noi parametri care sunt mult mai importanti. Astfel, prin însumarea fecunditatii specifice fiecarei vârste se poate calcula rata bruta a reproducerii, adica numarul de descendenti pe care un individ din populatie l-ar putea avea daca ar parcurge (ar trai) toate clasele de vârsta. În cazul prezentat mai sus valoarea acestui parametru este 1,66.

Rata reproducerii este mult mai importanta pentru studiul ecologic atunci când aceasta tine cont de numarul real mediu al descendentilor pe care îl are un individ decât de valoarea maxima a acestui numar. Aceasta valoare medie reprezinta rata neta a reproducerii (R₀). Produsul dintre supravietuire (l_x) si fecunditate (m_x) determina rata reproducerii la o anumita vârsta (l_xm_x), iar suma acestor valori pe parcursul tuturor vârstelor reprezinta rata neta a reproducerii sau numarul mediu de descendenti produsi de un individ de-a lungul întregii sale vieti.

În exemplul prezentat în tabelul de viata, valoarea neta a reproducerii este 846, valoare foarte mare, care de fapt înseamna ca fiecare individ din populatie poate da nastere la 423 de descendenti.

Un alt indice interesant ce poate fi determinat pornind de la tabelul de viata este vârsta generatiei care reprezinta de fapt vârsta medie la care indivizii produc jumatate din descendentii lor. Din exemplul de mai sus, rezulta ca aceasta valoare (T) este 1,681.

Rata bruta a reproducerii, rata neta a reproducerii si vârsta generatiei reprezinta valori care sunt capabile sa descrie populatia. De exemplu, rata bruta a reproducerii poate sa indice faptul ca, în conditii ideale, populatia medie (2 624 indivizi) poate produce 4 355 840 descendenti, în cazul ipotetic în care fiecare individ va atinge vârsta maxima si va produce numarul maxim de descendenti.

Rata bruta a reproducerii poate descrie ceea ce populatia poate de fapt sa realizeze din acest punct de vedere. Atunci când valoarea este 1, atunci individul mediu produce un singur descendent si deci populatia va ramâne constanta.

Tabelele de viata pot de asemenea sa furnizeze informatii asupra sperantei de viata (e_x) si valoare reproductiva (v_x) a indivizilor de diferite vârste. Calculul acestor doua marimi este mai laborios. Speranta de viata reprezinta suma tuturor valorilor supravietuirii de la vârsta x pâna la vârsta cea mai mare, împartita la supravietuirea la vârsta x. Valoarea reproductiva (v_x) se poate calcula prin însumarea tuturor produselor (l_xm_x) de la vârsta x pâna la ultima clasa de vârsta si împartirea rezultatului la valoarea l_x. În exemplul considerat, se poate observa cu usurinta ca indivizii din clasele de vârsta 1 si 2 prezinta cea mai mare cifra a valorii reproductive în cadrul populatiei, ceea ce poate însemna ca pentru o astfel de specie, selectia naturala a favorizat reproducerea cu succes a stadiilor tinere ale populatiei pentru care s-a construit tabelul de viata.

12.7. Tipuri de supravietuire

Daca se reprezinta grafic evolutia corelata a valorilor supravietuirii (lx) si vârstei (x) se obtin asa numitele curbe de supravietuire ale populatiei. În functie de modul de manifestare a ratei mortalitatii se pot diferenta în mod teoretic mai multe tipuri de curbe ale supravietuirii populatiilor (figura 44).

În cazul curbelor de tip I, forma generala a curbei supravietuirii este determinata de o rata mare a supravietuirii la toate vârstele cu exceptia vârstelor celor mai înaintate când rata supravietuirii scade foarte mult. În cazurile descrise de curba de tip II supravietuirea scade proportional cu înaintarea în vârsta. Curbele similare cu tipul III prezinta situatia descresterii constante a supravietuirii. Tipul IV descrie o supravietuire redusa la vârstele foarte tinere si o crestere constanta în continuare. În curbele caracteristice tipului V, supravietuirea este extrem de redusa la vârstele tinere pentru a creste rapid si ramâne relativ constanta.

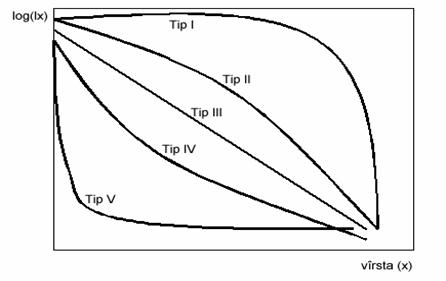
Fig. 44. Tipuri teoretice curbei de ale supravietuire a populatiilor

Evident, populatiile naturale prezinta curbe de supravietuire care sunt sensibil diferite de formele teoretice posibile prezentate mai sus si vor fi de fapt combinatii specifice ale acestora.